
第五章突触动力学Ⅱ:有监督学习 神经网络的分类 按网络结构分为:反馈网络和前馈网络: 按学习方式分为:监督学习和非监督学习。 本章主要论述前馈网络的监督学习算法,包括感知器 算法、最小均方误差算法和反向传播(BP)算法。 本章论述了监督学习是对未知平均误差层的随机近似, 即给定观察得到的随机矢量样本对: (x,y),(x22)2(xmym) 要估计一个未知函数:f:x一y,并且使期望误差函 数EJ]最小。误差定义为期望特性与实际特性之差
第五章 突触动力学Ⅱ:有监督学习 神经网络的分类 按网络结构分为:反馈网络和前馈网络; 按学习方式分为:监督学习和非监督学习。 本章主要论述前馈网络的监督学习算法,包括感知器 算法、最小均方误差算法和反向传播(BP) 算法。 本章论述了监督学习是对未知平均误差层的随机近似, 即给定观察得到的随机矢量样本对: 1 1 2 2 ( , ), ( , ), ( , ) m m x y x y x y 要估计一个未知函数:f : x—y,并且使期望误差函 数E[J]最小。误差定义为期望特性与实际特性之差
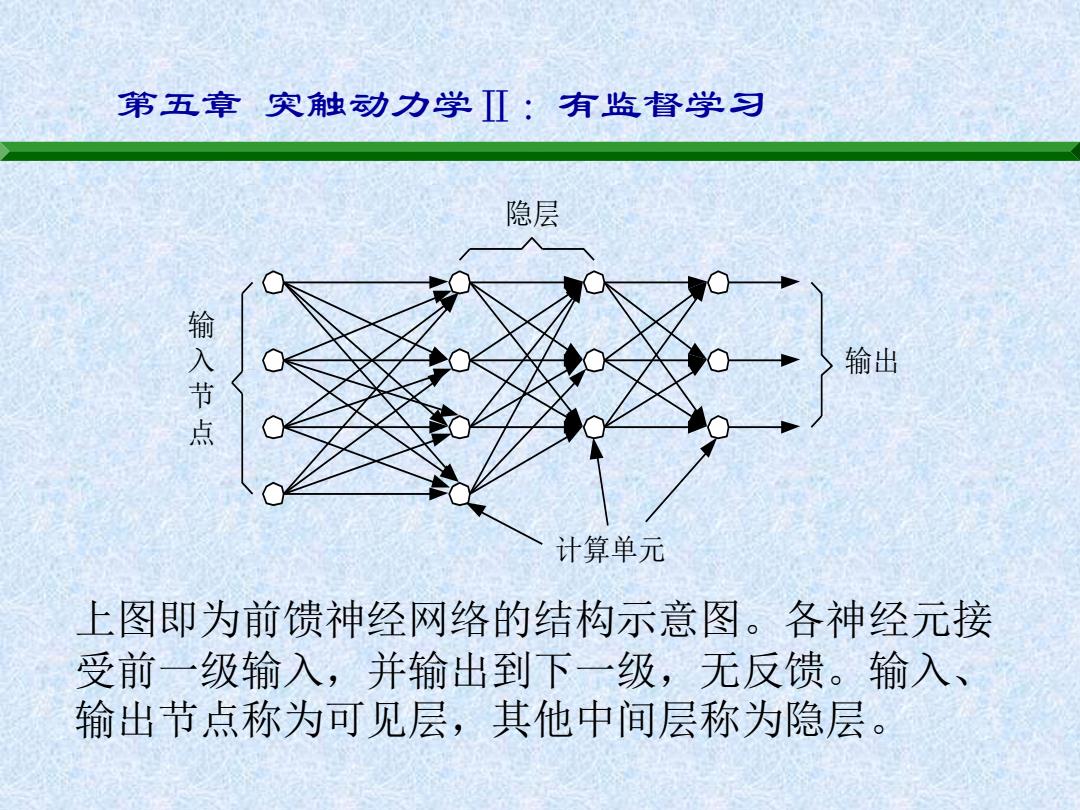
第五章突触动力学[:有监督学习 隐层 输入节点 输出 计算单元 上图即为前馈神经网络的结构示意图。各神经元接 受前一级输入,并输出到下一级,无反馈。输入、 输出节点称为可见层,其他中间层称为隐层
第五章 突触动力学Ⅱ:有监督学习 输出 隐层 输 入 节 点 计算单元 上图即为前馈神经网络的结构示意图。各神经元接 受前一级输入,并输出到下一级,无反馈。输入、 输出节点称为可见层,其他中间层称为隐层

第五章突触动力学Ⅱ:有监督学习 当现有的先验知识不完全时,就需要学习。学 习的方式取决于这一先验信息不完全的程度。在 监督学习过程中,假设已知未来学习系统的期望 响应,并且使用期望值与实际值的差值(即学习 系统的误差)去修正系统的行为。而在非监督学 习中是不了解学习系统的期望响应的。 神经网络通过向环境获取知识并改进自身性能。 般是按某种预定的度量调节自身的参数(如权 值)随时间逐步达到的
第五章 突触动力学Ⅱ:有监督学习 当现有的先验知识不完全时,就需要学习。学 习的方式取决于这一先验信息不完全的程度。在 监督学习过程中,假设已知未来学习系统的期望 响应,并且使用期望值与实际值的差值(即学习 系统的误差)去修正系统的行为。而在非监督学 习中是不了解学习系统的期望响应的。 神经网络通过向环境获取知识并改进自身性能。 一般是按某种预定的度量调节自身的参数(如权 值)随时间逐步达到的
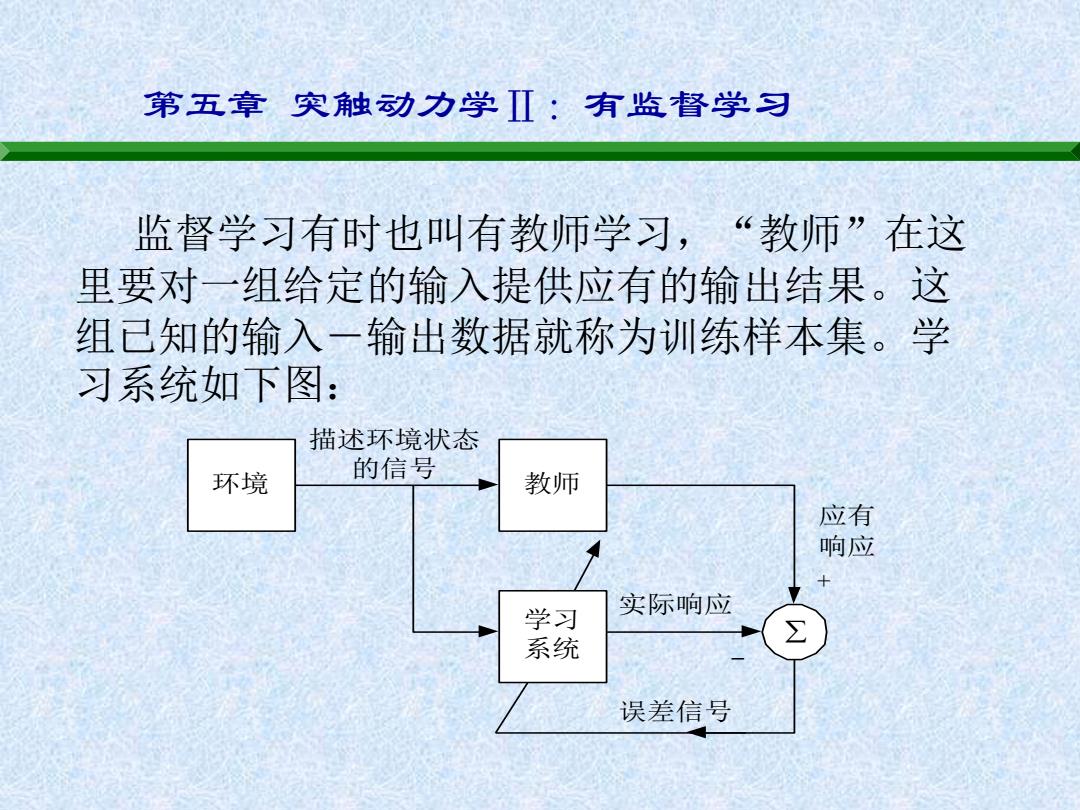
第五章突触动力学Ⅱ:有监督学习 监督学习有时也叫有教师学习,“教师”在这 里要对一组给定的输入提供应有的输出结果。这 组己知的输入一输出数据就称为训练样本集。学 习系统如下图: 描述环境状态 环境 的信号 教师 应有 响应 学习 实际响应 系统 误差信号
第五章 突触动力学Ⅱ:有监督学习 监督学习有时也叫有教师学习,“教师”在这 里要对一组给定的输入提供应有的输出结果。这 组已知的输入-输出数据就称为训练样本集。学 习系统如下图: 环境 教师 学习 系统 实际响应 误差信号 应有 响应 描述环境状态 的信号 + -

第五章突触动力学Ⅱ:有监督学习 非监督学习不存在外部教师,学习系统完全按照 环境所提供数据的某些统计规律来调节自身参数或 结构(这是一种自组织过程),以表示外部输入的某 种固有特征,如聚类。 学习算法主要有: 1、Hebb学习算法: △w(n)=F(yk(n),x,(n) 2、竞争学习算法: A() c(x-wn), 若神经元j获胜 0, 若神经元j失败 3、误差纠正学习算法
第五章 突触动力学Ⅱ:有监督学习 非监督学习不存在外部教师,学习系统完全按照 环境所提供数据的某些统计规律来调节自身参数或 结构(这是一种自组织过程),以表示外部输入的某 种固有特征,如聚类。 学习算法主要有: 1、Hebb学习算法: ( ) ( ( ), ( )) = w n F y n x n kj k j 2、竞争学习算法: ( ), ( ) 0 j ji kj c x w w n − = , 3、误差纠正学习算法 若神经元 j 获胜 若神经元 j 失败

第五章突触动力学Ⅱ:有监督学习 下面从不同角度分析监督学习: 1、有监督函数估计 神经网络引进的函数估计的概念为:已知随机样 本矢量对(x,y),(xm,ym),要从这些样本中估计 出产生这些样本矢量对的函数,即: f:x→y 其中:x,∈xcR” 是输入空间 y,∈ycRP 是输出空间 f 是要估计的泛函 所采用的方法为是使一个未知期望的误差函数E(J) (也叫目标函数)最小化
第五章 突触动力学Ⅱ:有监督学习 1、有监督函数估计 神经网络引进的函数估计的概念为:已知随机样 本矢量对 1 1 , ), ( , ) m m (x y x y ,要从这些样本中估计 出产生这些样本矢量对的函数 f ,即: 下面从不同角度分析监督学习: f x y : → 其中: n i x x R 是输入空间 p i y y R 是输出空间 f 是要估计的泛函 所采用的方法为是使一个未知期望的误差函数 E J( ) (也叫目标函数)最小化

第五章突触动力学Ⅱ:有监督学习 2、作为有效条件的有监督学习 有效条件强化响应(Operant conditioning reinforce responses)。条件聚类强化了刺激,例如,一个生物 体学会了一刺激响应对:S→R,那么在条件刺激S 中加一个条件B进行学习,即: (B&S)-→R或B→(S→R) 这样不断强化刺激,直到输入B时反应为R。这样就 有:B→R也就是学会了一条规则。这样的例子如 巴普洛夫条件反射试验
第五章 突触动力学Ⅱ:有监督学习 2、作为有效条件的有监督学习 有效条件强化响应(Operant conditioning reinforce responses)。条件聚类强化了刺激,例如,一个生物 体学会了一刺激响应对: S R → ,那么在条件刺激 S 中加一个条件 B 进行学习,即: ( & ) ( ) B S R B S R → → → 或 这样不断强化刺激,直到输入 B 时反应为 R。这样就 有: B R → 也就是学会了一条规则。这样的例子如 巴普洛夫条件反射试验

第五章突触动力学Ⅱ:有监督学习 3、用已知的类隶属度作为随机模式学习的有监督学习 模式:定义为模式空间R”的一个点; 时变模式:空间R”中的一条轨迹线: 映射x:[O,T]>R”定义了从时间区间[0,T]到模式 空间R”中单点的映射。 概率密度(x)为模式x在R”中的分布的一种描述 模式类:为空间R”的子集 现在的任务是用已知的样本x(1),x(2)·及模式类, 估计p(x)
第五章 突触动力学Ⅱ:有监督学习 3、用已知的类隶属度作为随机模式学习的有监督学习 模式:定义为模式空间 的一个点; n R 时变模式:空间 n R 中的一条轨迹线; 映射 :[0, ] n x T R → 定义了从时间区间 [0, ] T 到模式 空间 n R 中单点的映射。 概率密度 p x( ) 为模式 x 在 n R 中的分布的一种描述 模式类:为空间 n R 的子集 现在的任务是用已知的样本 x x (1), (2) 及模式类, 估计 p x( )

第五章突触动力学Ⅱ:有监督学习 定义I,:R”→{0,1}是集合S的指示函数: () 1 x∈S xeS 指示函数指出了模式x的类隶属度。如果S是将R” 映射到[0,1]而不是{0,1},那么S就是一个连续的 或者说多值的(模糊的)集合,即模式x以不同的程 度隶属于不同的类。 假设将模式样本空间R”分为k个不相交的子集: R”=DUD2UDk且D,∩D,=Φ如果i≠j
第五章 突触动力学Ⅱ:有监督学习 定义 : {0,1} n s I R → 是集合 S 的指示函数: 1 ( ) 0 s x S I x x S = 指示函数指出了模式 x 的类隶属度。如果 S 是将 n R 映射到 [0,1] 而不是 {0,1} ,那么 S 就是一个连续的 或者说多值的(模糊的)集合,即模式 x 以不同的程 度隶属于不同的类。 假设将模式样本空间 n R 分为 k 个不相交的子集: 1 2 n R D D D D D i j = = k i j 且 如果

第五章突触动力学Ⅱ:有监督学习 则类概率密度为: P(D,)=5 p(x)dx=ELIo1 E为求期望值,且有: P(D)=1 i=1 有监督和无监督模式学习的区别依赖于已有的信息以 及学习系统如何利用它。在两种情况下系统都不知道(x) 如果知道确定的类,并且学习系统利用了这些信息,那 么模式学习就是监督学习。如果不知道或没用类隶属度 (指示函数),则模式学习就是非监督的
第五章 突触动力学Ⅱ:有监督学习 则类概率密度为: ( ) ( ) [ ] i i i D D P D p x dx E I = = E 为求期望值,且有: 1 ( ) 1 k i i P D = = 有监督和无监督模式学习的区别依赖于已有的信息以 及学习系统如何利用它。在两种情况下系统都不知道 p x( ) 如果知道确定的类,并且学习系统利用了这些信息,那 么模式学习就是监督学习。如果不知道或没用类隶属度 (指示函数),则模式学习就是非监督的