
Chapter 8 Fuzzy Associative Memories Li Lin 2004-11-24
Chapter 8 Fuzzy Associative Memories Li Lin 2004-11-24

CONTENTS Review a Fuzzy Systems as between-cube mapping Fuzzy and Neural Function Estimators Fuzzy Hebb FAMs ■Adaptive FAMs
CONTENTS ◼ Review ◼ Fuzzy Systems as between-cube mapping ◼ Fuzzy and Neural Function Estimators ◼ Fuzzy Hebb FAMs ◼ Adaptive FAMs

Review In Chapter 2,we have mentioned BAM theorem Chapter 7 discussed fuzzy sets as points in the unit hypercube What is associative memories?
Review ◼ In Chapter 2, we have mentioned BAM theorem ◼ Chapter 7 discussed fuzzy sets as points in the unit hypercube ◼ What is associative memories?
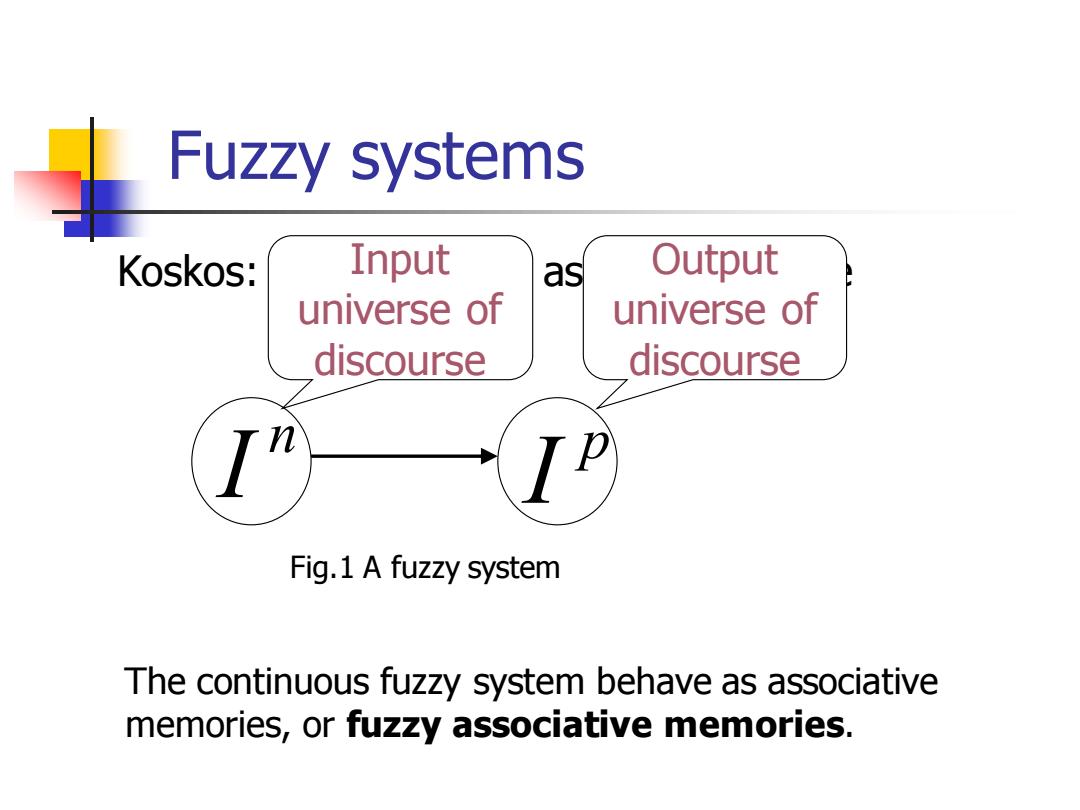
Fuzzy systems Koskos: Input as Output universe of universe of discourse discourse Fig.1 A fuzzy system The continuous fuzzy system behave as associative memories,or fuzzy associative memories
Fuzzy systems Koskos: fuzzy systems as between-cube mapping n I p I Fig.1 A fuzzy system Output universe of discourse Input universe of discourse The continuous fuzzy system behave as associative memories, or fuzzy associative memories

Fuzzy and neural function estimators Fuzzy and neural systems estimates sampled function and behave as associative memories Similarities: 1.They are model-free estimator 2.Learn from samples 3.Numerical,unlike AI Differences: They differ in how to estimate the sampled function 1.During the system construction 2.The kind of samples used
Fuzzy and neural function estimators ◼ Fuzzy and neural systems estimates sampled function and behave as associative memories ◼ Similarities: 1. They are model-free estimator 2. Learn from samples 3. Numerical, unlike AI ◼ Differences: They differ in how to estimate the sampled function 1. During the system construction 2. The kind of samples used
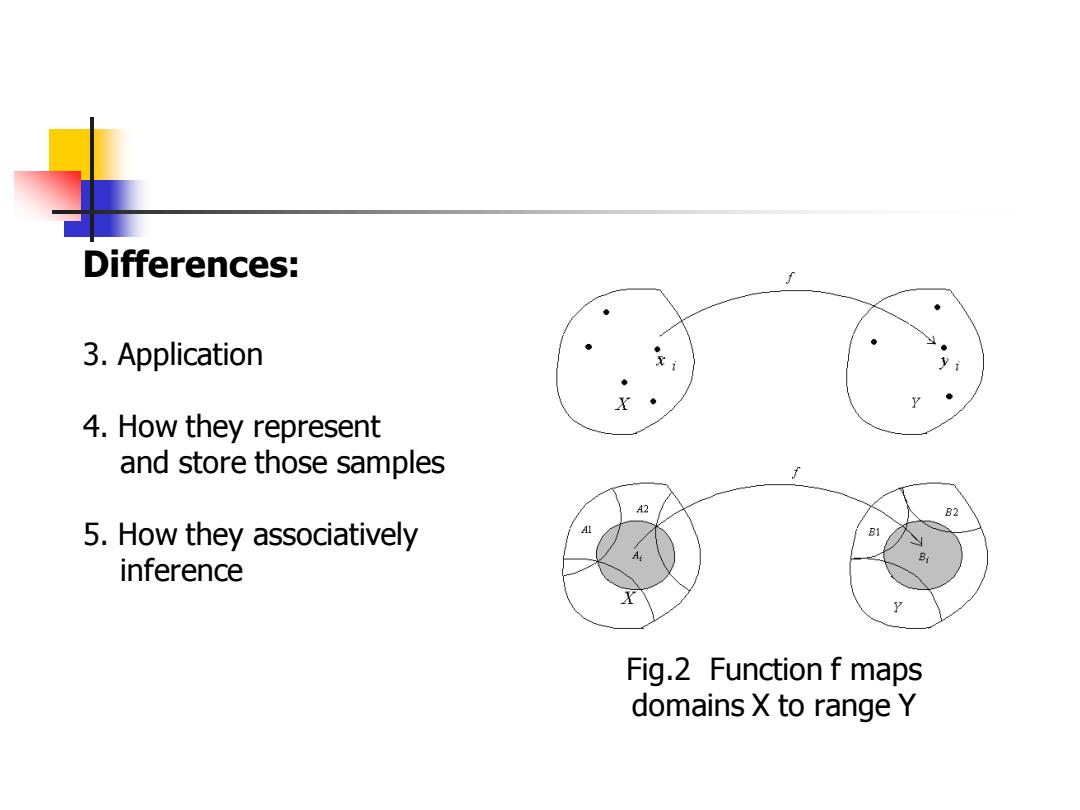
Differences: 3.Application 4.How they represent and store those samples A2 B2 5.How they associatively inference Fig.2 Function f maps domains X to range Y
Fig.2 Function f maps domains X to range Y 3. Application 4. How they represent and store those samples 5. How they associatively inference Differences:

Neural vs.fuzzy representation of structured knowledge ■Neural network problems: 1.computational burden of training 2.system inscrutability There is no natural inferential audit tail,like an computational black box. 3.sample generation
Neural vs. fuzzy representation of structured knowledge ◼ Neural network problems: 1. computational burden of training 2. system inscrutability There is no natural inferential audit tail, like an computational black box. 3. sample generation

Neural vs.fuzzy representation of structured knowledge Fuzzy systems 1.directly encode the linguistic sample (HEAVY,LONGER)in a matrix 2.combine the numerical approaches with the symbolic one Fuzzy approach does not abandon neural-network, it limits them to unstructured parameter and state estimate,pattern recognition and cluster formation
Neural vs. fuzzy representation of structured knowledge ◼ Fuzzy systems 1. directly encode the linguistic sample (HEAVY,LONGER) in a matrix 2. combine the numerical approaches with the symbolic one ◼ Fuzzy approach does not abandon neural-network, it limits them to unstructured parameter and state estimate, pattern recognition and cluster formation

FAMs as mapping ■ Fuzzy associative memories are transformations FAM map fuzzy sets to fuzzy sets,units cube to units cube. Access the associative matrices in parallel and store them separately Numerical point inputs permit this simplification binary input-out FAMs,or BIOFAMs
FAMs as mapping ◼ Fuzzy associative memories are transformations FAM map fuzzy sets to fuzzy sets, units cube to units cube. ◼ Access the associative matrices in parallel and store them separately Numerical point inputs permit this simplification binary input-out FAMs, or BIOFAMs
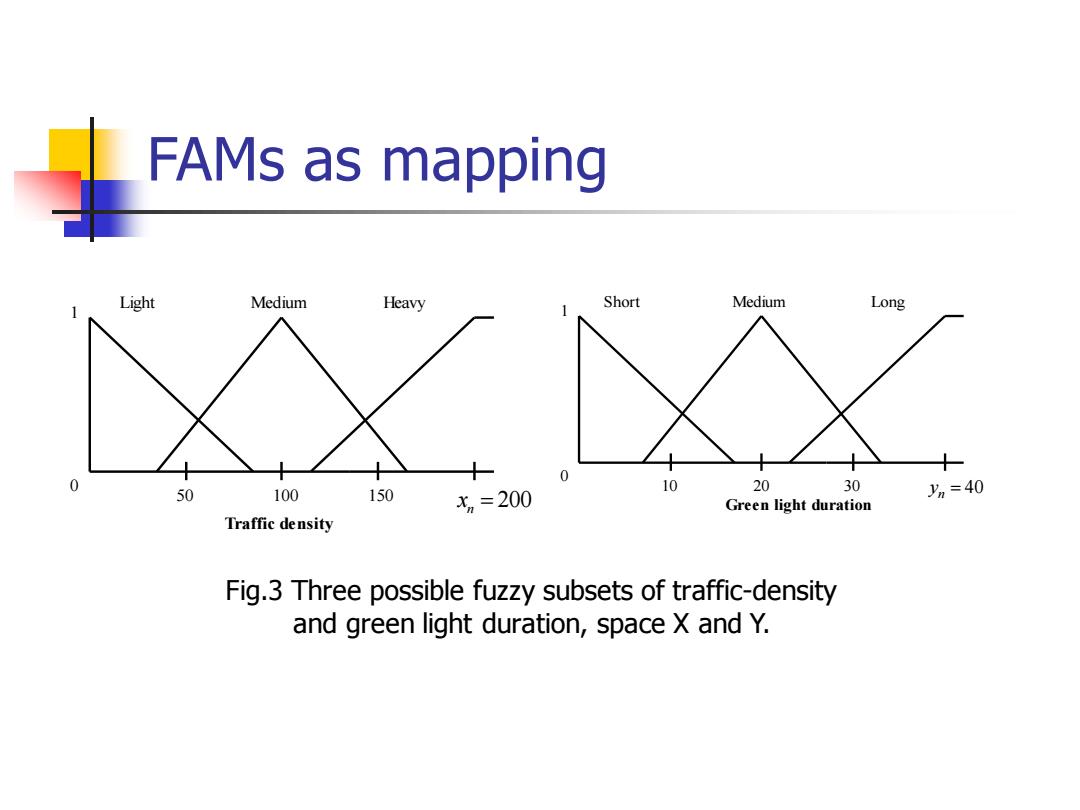
FAMs as mapping Light Medium Heavy Short Medium Long 0 0 10 20 30 50 100 150 xn=200 ym=40 Green light duration Traffic density Fig.3 Three possible fuzzy subsets of traffic-density and green light duration,space X and Y
FAMs as mapping = 200 n x 50 100 150 0 1 Light Medium Heavy Traffic density = 40 n 10 20 30 y 0 1 Short Medium Long Green light duration Fig.3 Three possible fuzzy subsets of traffic-density and green light duration, space X and Y