
模糊与卡尔曼滤波日标跟踪控制系统的比较 Comparison of Fuzzy and Kalman-Filter Target-Tracking control system Peter J.Pacini,Bart Kosko 报告人:黄健斌
模糊与卡尔曼滤波目标跟踪控制系统的比较 Comparison of Fuzzy and Kalman-Filter Target-Tracking control system 报告人:黄健斌 Peter J.Pacini , Bart Kosko

内容简个 1、为什么要将模糊控制器与卡尔曼滤波器进行比较? 2、实时目标跟踪系统是怎样的? 3、模糊控制器的工作原理是怎样的? 4、卡尔曼滤波器与模糊控制器在目标跟踪系统中性能如何?
1、为什么要将模糊控制器与卡尔曼滤波器进行比较? 3、模糊控制器的工作原理是怎样的? 2、实时目标跟踪系统是怎样的? 内容简介 4、卡尔曼滤波器与模糊控制器在目标跟踪系统中性能如何?

1、为什么要将模糊控制器与卡尔曼滤波器进行比较? 卡尔曼滤波器是一 模糊控制器是 种理想的随机线性自适 个模糊系统, 应滤波器,它需要明确 其输出与输入之 的数据模型来定义输出 间没有经典的数 与输入之间的关系,是 学模型。 数据模型控制器的典范 (Benchmark) 没有系统是万能的,Benchmark也不例外
1、为什么要将模糊控制器与卡尔曼滤波器进行比较? 卡尔曼滤波器是一 种理想的随机线性自适 应滤波器,它需要明确 的数据模型来定义输出 与输入之间的关系,是 数据模型控制器的典范 (Benchmark)。 模糊控制器是 一个模糊系统, 其输出与输入之 间没有经典的数 学模型。 没有系统是万能的,Benchmark也不例外

数学模型控制器的问题 数学模型控制器在输出和输入的函数关系确定的情况下的 工作性能会很好。对于不确定的环境,数学模型控制器一般 采用概率统计量(条件均值、协方差等)来进行处理,实践 中常采用线性或马尔科夫模型。存在以下问题: (1)不确定性一般很难用经典数据模型加以准确描述。 (2)很难将专家的知识加到系统中去,在这种系统中, 专家的知识一般只能用来估计初始状态和协方差条件。 不确定环境,正是模糊大有用武之地
数学模型控制器的问题 数学模型控制器在输出和输入的函数关系确定的情况下的 工作性能会很好。对于不确定的环境,数学模型控制器一般 采用概率统计量(条件均值、协方差等)来进行处理,实践 中常采用线性或马尔科夫模型。存在以下问题: (1)不确定性一般很难用经典数据模型加以准确描述。 (2)很难将专家的知识加到系统中去,在这种系统中, 专家的知识一般只能用来估计初始状态和协方差条件。 不确定环境,正是模糊大有用武之地

2、实时目标跟踪系统是怎样的? 实时目标跟踪系统一般采用雷达或其它设备去探测目标与设备所 在平面的的高度和方位角。由两个马达控制设备的探测方向,通过连 续地调整两个马达的转速,保持对目标的连续跟踪。 对高度和方位角的控制可以采用相同的算法进行
2、实时目标跟踪系统是怎样的? 实时目标跟踪系统一般采用雷达或其它设备去探测目标与设备所 在平面的的高度和方位角。由两个马达控制设备的探测方向,通过连 续地调整两个马达的转速,保持对目标的连续跟踪。 对高度和方位角的控制可以采用相同的算法进行
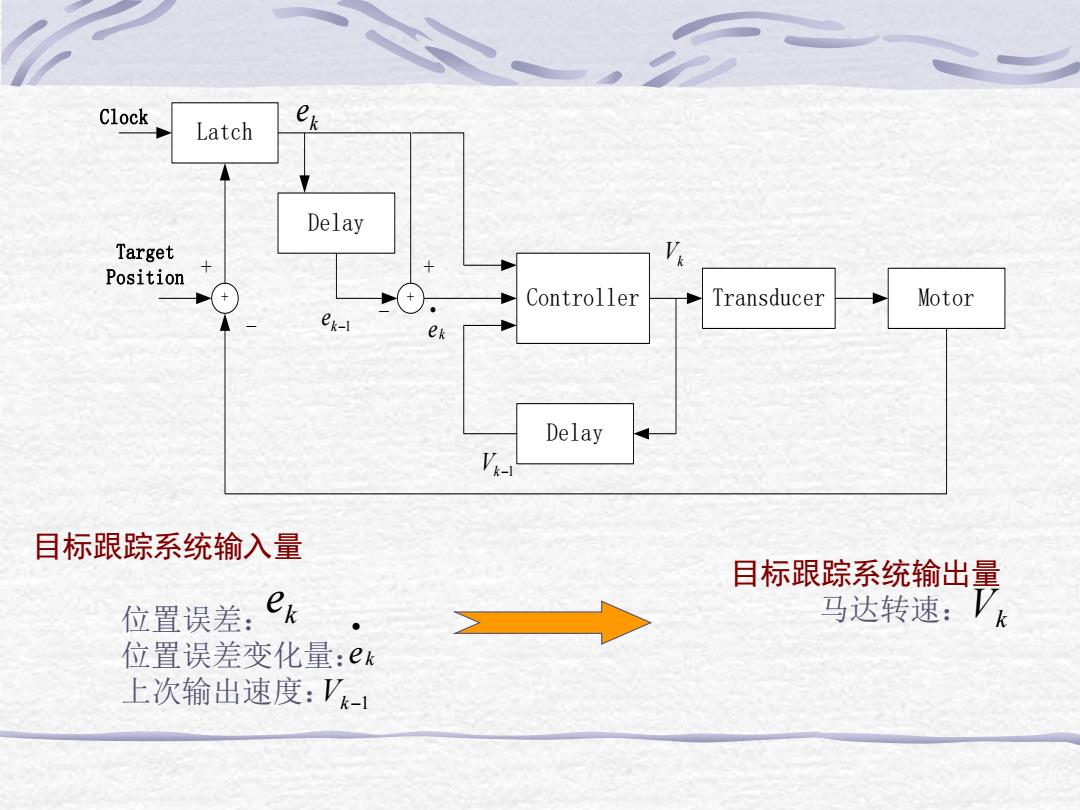
Clock Latch Delay Target Position Controller Transducer Motor ek-i ek Delay V 目标跟踪系统输入量 目标跟踪系统输出量 位置误差:ek 马达转速:7 位置误差变化量:ek 上次输出速度:Vk-1
目标跟踪系统输入量 位置误差: 位置误差变化量: 上次输出速度: 目标跟踪系统输出量 e k 马达转速: e k • Vk − 1 Vk Latch Delay Controller Delay + + Transducer Motor Clock Target Position + - k e ek • Vk−1 Vk k−1 e + -

3、模糊控制器的工作原理是怎样的? 模糊控制器是一个模糊系统。 有限模糊集合A可以抽象为单位超立方体I”=[O,]” 中的一点。 Tn包含域空间X=(x,x,x,)x,∈[0,1]的所有子集。 模糊系统的核心功能 输入模糊集 Y 输出模糊集 X∈I” Y∈IP
3、模糊控制器的工作原理是怎样的? 有限模糊集合A可以抽象为单位超立方体 中的一点。 ( , ,..., ) [0,1] X = x1 x2 xn xi n n I = [0,1] n I 模糊控制器是一个模糊系统。 包含域空间 的所有子集。 X Y n X I p Y I 输 模糊系统的核心功能 入 模 糊 集 输 出 模 糊 集
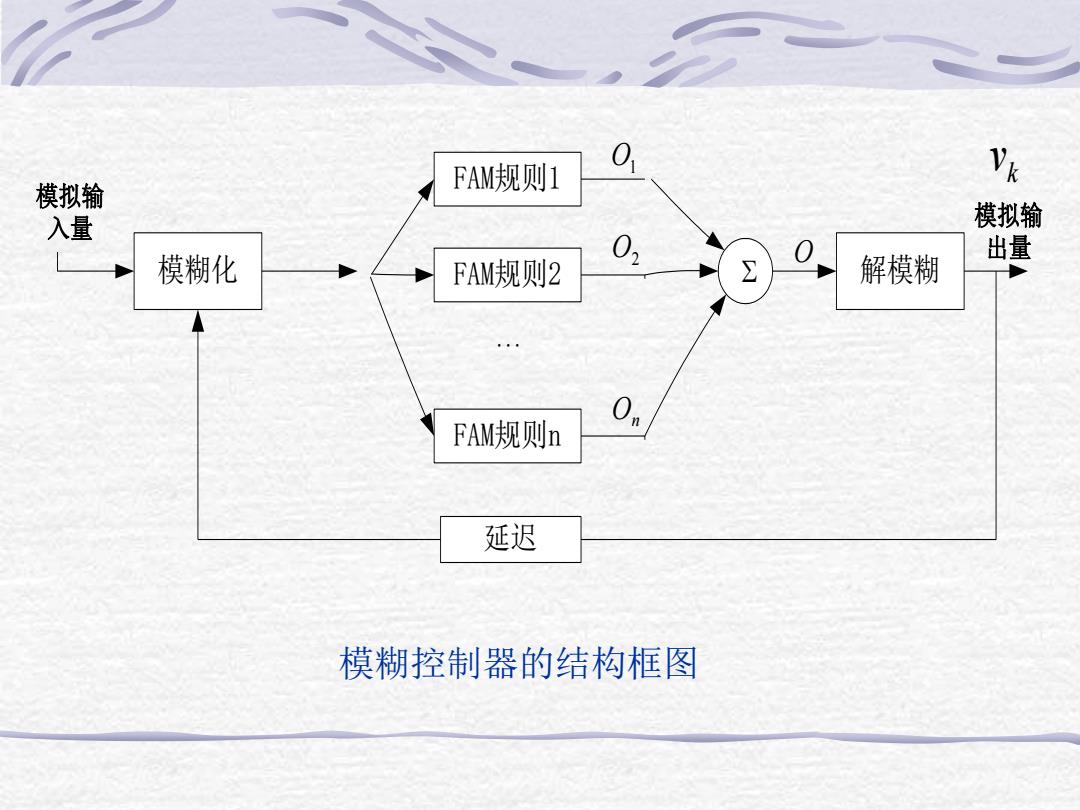
FAM规则1 01 VR 模拟输 入量 模拟输 出量 模糊化 02 FAM规则2 解模糊 FAM规则n 延迟 模糊控制器的结构框图
模糊化 解模糊 模拟输 入量 FAM规则1 FAM规则2 FAM规则n ... 模拟输 出量 O1 O2 On O k v 延迟 模糊控制器的结构框图

(1)输入量的模糊化 -6 LN:Large Negative -4 MN:Medium Negative -2 SN:Small Negative 输出角速度:[「6,6] 0 ZE:Zero 2 SP:Small Positive 4 MP:Medium Positive 6 LP:Large Positive 给定一个输入量,将其归入(一6,6)区间后,可以用某 些特定的函数计算其属于某个集合的隶属度
(1)输入量的模糊化 输出角速度:[-6,6] -6 LN: Large Negative MN: Medium Negative SN: Small Negative ZE: Zero SP: Small Positive MP: Medium Positive LP: Large Positive -4 -2 0 2 4 6 给定一个输入量,将其归入(-6,6)区间后,可以用某 些特定的函数计算其属于某个集合的隶属度
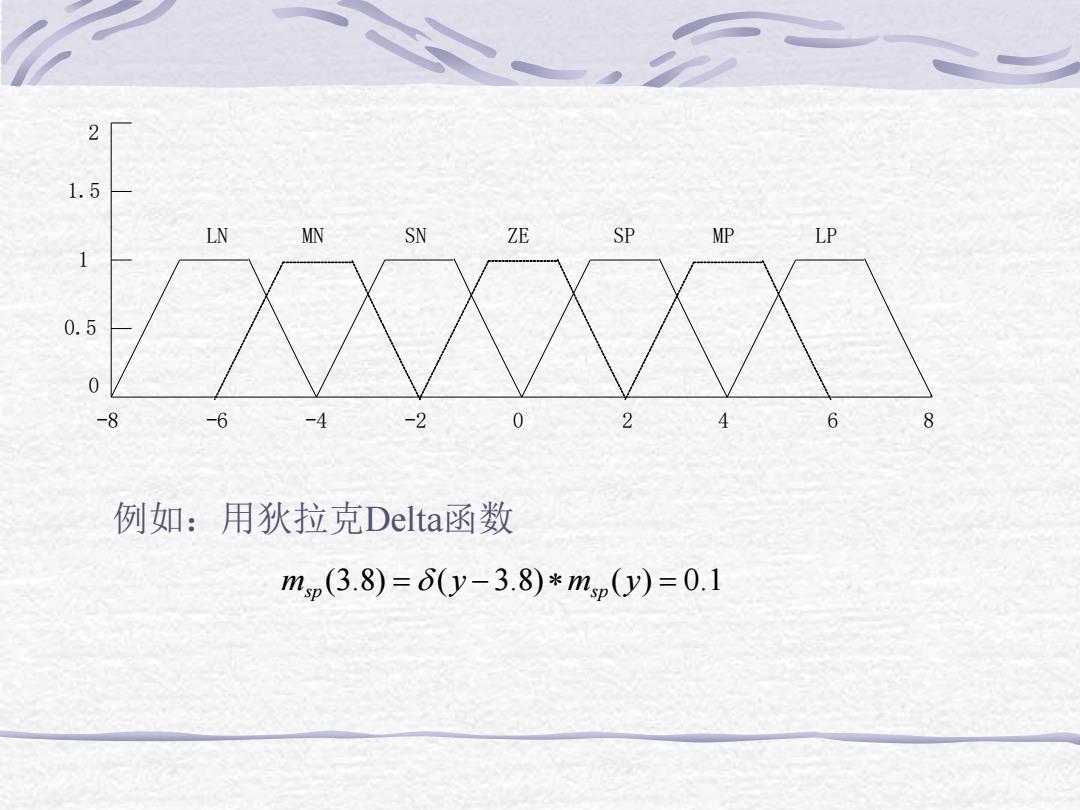
2 1.5 LN MN SN ZE SP MP LP 1 0 -8 -6 -4 -2 0 2 4 6 8 例如:用狄拉克Delta函数 mp(3.8)=y-3.8)*mp(y)=0.1
0 0.5 1 1.5 2 -8 -6 -4 -2 0 2 4 6 8 LN MN SN ZE SP MP LP 例如:用狄拉克Delta函数 ms p (3.8) = ( y −3.8)ms p ( y) = 0.1