
神经网络与模糊系统 Chapter 6 Architecture and Equilibria 结构和平衡 学生:李琦 导师:高新波
Architecture and Equilibria 结构和平衡 Chapter 6 神经网络与模糊系统 学生: 李 琦 导师:高新波

6.1 Neutral Network As Stochastic Gradient system Classify Neutral network model By their synaptic connection topologies and by how learning modifies their connection topologies synaptic connection topologies 1.feedforward:if no closed synaptic loops 2.feedback:if closed synaptic loops or feedback pathways how learning modifies their connection topologies 1.Supervised learning:use class-membership information of training samples 2Unsupervised learning:use unlabelled training samplings 2003.11.19 2
2003.11.19 2 6.1 Neutral Network As Stochastic Gradient system Classify Neutral network model By their synaptic connection topologies and by how learning modifies their connection topologies 1. : 2. : feedforward if no closed synaptic loops feedback if closed synaptic loops or feedback pathways 1. : 2. : Supervised learning use class membership information of training samples Unsupervised learning use unlabelled training samplings − synaptic connection topologies how learning modifies their connection topologies
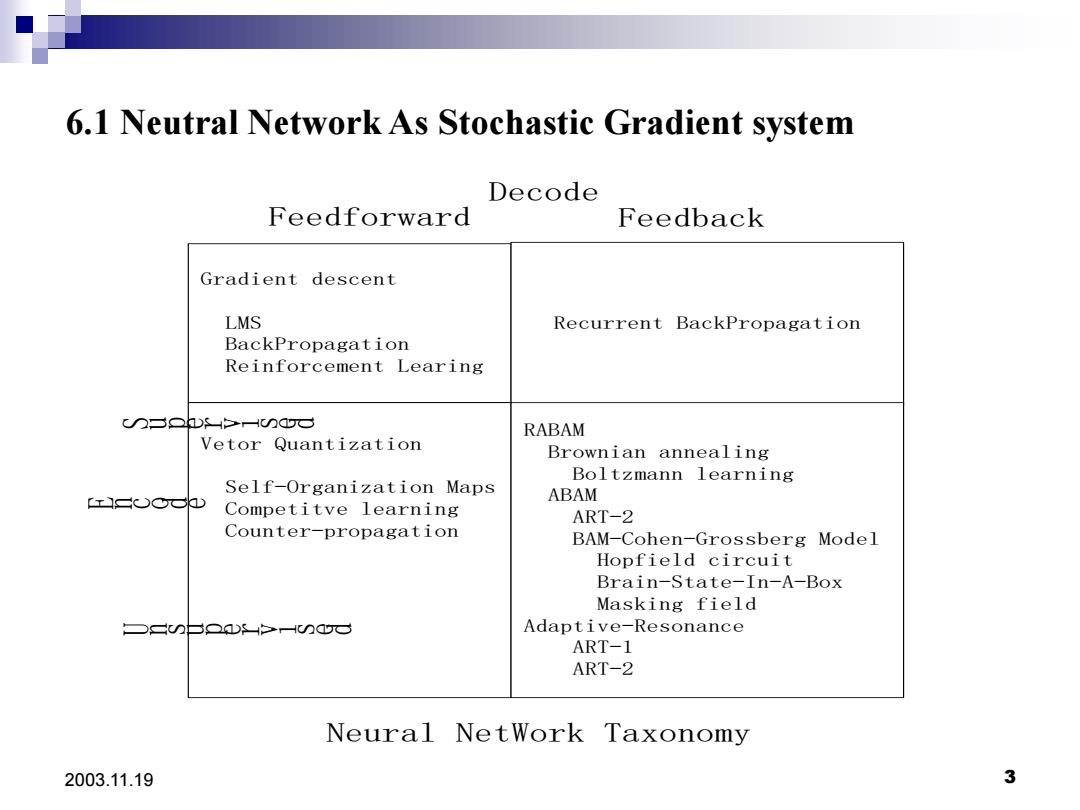
6.1 Neutral Network As Stochastic Gradient system Decode Feedforward Feedback Gradient descent LMS Recurrent BackPropagation BackPropagation Reinforcement Learing C∽=Qh>H∽aa RABAM Vetor Quantization Brownian annealing Boltzmann learning Self-Organization Maps rsooo ABAM Competitve learning ART-2 Counter-propagation BAM-Cohen-Grossberg Model Hopfield circuit Brain-State-In-A-Box Masking field ○二∽台QaDs>H∽qG Adaptive-Resonance ART-1 ART-2 Neural NetWork Taxonomy 2003.11.19 3
2003.11.19 3 6.1 Neutral Network As Stochastic Gradient system Gradient descent LMS BackPropagation Reinforcement Learing Recurrent BackPropagation Vetor Quantization Self-Organization Maps Competitve learning Counter-propagation RABAM Brownian annealing Boltzmann learning ABAM ART-2 BAM-Cohen-Grossberg Model Hopfield circuit Brain-State-In-A-Box Masking field Adaptive-Resonance ART-1 ART-2 Feedforward Feedback Decode S u p e r v i s e d U n s u p e r v i s e d E n c o d e Neural NetWork Taxonomy

6.2 Global Equilibria:convergence and stability Three dynamical systems in neural network: synaptic dynamical system N neuronal dynamical system joint neuronal-synaptic dynamical system (M) Historically,Neural engineers study the first or second neural network.They usually study learning in feedforward neural networks and neural stability in nonadaptive feedback neural networks.RABAM and ART network depend on joint equilibration of the synaptic and neuronal dynamical systems. 2003.11.19 4
2003.11.19 4 6.2 Global Equilibria: convergence and stability Three dynamical systems in neural network: synaptic dynamical system neuronal dynamical system joint neuronal-synaptic dynamical system Historically,Neural engineers study the first or second neural network.They usually study learning in feedforward neural networks and neural stability in nonadaptive feedback neural networks. RABAM and ART network depend on joint equilibration of the synaptic and neuronal dynamical systems. M x ( , ) x M

6.2 Global Equilibria:convergence and stability Equilibrium is steady state(for fixed-point attractors) Convergence is synaptic equilibrium.M=0 Stability is neuronal equilibrium.*=0 More generally neural signals reach steady state even though the activations still change.We denote steady state in the neuronal field F:F=0 Global stability:x=0,M=0 Stability-Equilibrium dilemma Neurons fluctuate faster than synapses fluctuate. Convergence undermines stability. 2003.11.19 5
2003.11.19 5 6.2 Global Equilibria: convergence and stability Equilibrium is steady state (for fixed-point attractors) Convergence is synaptic equilibrium. Stability is neuronal equilibrium. More generally neural signals reach steady state even though the activations still change. We denote steady state in the neuronal field : Global stability: Stability - Equilibrium dilemma : Neurons fluctuate faster than synapses fluctuate. Convergence undermines stability. Μ = 0 x = 0 F x Fx = 0 x = 0,M = 0

6.3 Synaptic convergence to centroids:AVQ Algorithms Competitive learning adaptively quantizes the input pattern space R".Probability density function p(x)characterizes the continuous distributions of patterns in R. We shall prove that competitive AVQ synaptic vector m, converge exponentially quickly to pattern-class centroids and. more generally,at equilibrium they vibrate about the centroids in a Browmian motion 2003.11.19 6
2003.11.19 6 6.3 Synaptic convergence to centroids: AVQ Algorithms We shall prove that competitive AVQ synaptic vector converge exponentially quickly to pattern-class centroids and, more generally, at equilibrium they vibrate about the centroids in a Browmian motion. m j Competitive learning adaptively quantizes the input pattern space . Probability density function characterizes the continuous distributions of patterns in . n R p(x) n R

6.3 Synaptic convergence to centroids:AVQ Algorithms Competitive AVQ Stochastic Differential Equations: R”=DUD2UD3.UDk D:∩Dj=D,fi≠j The Random Indicator function ()xED 0fx廷D Supervised learning algorithms depend explicitly on the indicator functions.Unsupervised learning algorithms don't require this pattern-class information. Centriod of Di ∫D.p(x) X,= p(x)dx 2003.11.19 7
2003.11.19 7 6.3 Synaptic convergence to centroids: AVQ Algorithms 1 2 3.... , k n R D D D D D D if i j i j = = The Random Indicator function Supervised learning algorithms depend explicitly on the indicator functions.Unsupervised learning algorithms don’t require this pattern-class information. Centriod of : 1 ( ) 0 j j D j if x D I x if x D = ( ) ( ) j j D j D xp x dx x p x dx = Competitive AVQ Stochastic Differential Equations: Dj

6.3 Synaptic convergence to centroids:AVQ Algorithms The Stochastic unsupervised competitive learning law: m;=S,y儿x-m,]+nj We want to show that at equilibrium m=x or E(m)=x As discussed in Chapter 4:S (x) The linear stochastic competitive learning law: m,=1o,(xx-m,]+n) The linear supervised competitive learning law: ri,=r(x)Ip (x)[x-mjl+n ,(x)=1p,(x)-∑1(x) 2003.11.19 8
2003.11.19 8 6.3 Synaptic convergence to centroids: AVQ Algorithms The Stochastic unsupervised competitive learning law: ( )[ ] m S y x m n j j j j j = − + We want to show that at equilibrium or E( ) m x m x j j j j = = ( ) j j D As discussed in Chapter 4: S I x The linear stochastic competitive learning law: ( )[ ] j j D j j m = − + I x x m n The linear supervised competitive learning law: ( )[ ] ( ) ( ) ( ) ( ) j j i j j D j j j D D i j r I x x m n r I x I x m x x = − + = −

6.3 Synaptic convergence to centroids:AVQ Algorithms The linear differential competitive learning law: m,=S,[x-mj1+nj In practice: in,=sgn[yx-mjl+nj 1 讨z>0 讨z=0 2003.11.19 9
2003.11.19 9 6.3 Synaptic convergence to centroids: AVQ Algorithms The linear differential competitive learning law: In practice: [ ] m S x m n j j j j = − + sgn[ ][ ] 1 0 sgn[ ] 0 0 1 0 m y x m n j j j j if z z if z if z = − + = = −

6.3 Synaptic convergence to centroids:AVQ Algorithms Competitive AVQ Algorithms 1.Initialize synaptic vectors:m(0)=x(i),i=1,......,m 2.For random sample x(t),find the closest (winning)synaptic vector m (t):m,(t)-x(t)=minlm,(t)-x(t where+gives the squared Euclidean norm of x 3.Update the wining synaptic vectors m()by the UCL,SCL,or DCL learning algorithm. 2003.11.19 10
2003.11.19 10 6.3 Synaptic convergence to centroids: AVQ Algorithms Competitive AVQ Algorithms 1. Initialize synaptic vectors: mi (0) = x(i) , i =1,......,m 2.For random sample , find the closest (“winning”) synaptic vector : x(t) m (t) j ( ) ( ) min ( ) ( ) j i i m t x t m t x t − = − 3.Update the wining synaptic vectors by the UCL ,SCL,or DCL learning algorithm. m (t) j 2 2 2 1 ....... where x x x = + + n gives the squared Euclidean norm of x