
第七章模糊与概率 陶晓燕
第七章 模糊与概率 陶晓燕

本章的主要问题: ·模糊和概率的基本知识 模糊集合的几何图示 ·模糊集合的大小的表征 ?·模糊集合的模糊程度的度量 ?· 模糊集合间的包含关系 ?、 模糊集合间的包含关系与模糊集 合的模糊程度之间的关系
本章的主要问题: • 模糊和概率的基本知识 • 模糊集合的几何图示 • 模糊集合的大小的表征 • 模糊集合的模糊程度的度量 • 模糊集合间的包含关系 • 模糊集合间的包含关系与模糊集 合的模糊程度之间的关系

一、模糊和概率的基本知识 1.是否不确定性就是随机性?概率的概念是否包含了所有的不确 定性的概念? Bayesian camp:概率是一种主观的先验知识,不是一种频率 和客观测量值 Lindley::概率是对不确定性唯一有效并充分的描述,所有其 他方法都是不充分的(直接指向模糊理论) 随机和模糊在概念和理论上都是有区别的 相似:通过单位间隔[0,1]间的数来表述不确定性,都兼有集 合和命题的结合律、交换律、分配律 区别: 对待A∩A。经典集合论,A∩A=中,P(A∩A)=P()=0 代表概率上不可能的事件。而模糊建立在A⌒A°≠中
一、模糊和概率的基本知识 1.是否不确定性就是随机性?概率的概念是否包含了所有的不确 定性的概念? Bayesian camp:概率是一种主观的先验知识,不是一种频率 和客观测量值 Lindley:概率是对不确定性唯一有效并充分的描述,所有其 他方法都是不充分的(直接指向模糊理论) 随机和模糊在概念和理论上都是有区别的 相似:通过单位间隔[0,1]间的数来表述不确定性,都兼有集 合和命题的结合律、交换律、分配律 区别:对待 。经典集合论, 代表概率上不可能的事件。而模糊建立在 c A A , ( ) ( ) 0 c c A A P A A P = = = c A A

考虑两个问题: (1)A⌒A=总是真的吗?(模糊存在吗) 考虑是否逻辑上或实际中有违背“无矛盾定理”的现象 (Aristotlel的三个‘思考定理’之一,另外两个是‘排中定 理'AUA=X,‘同一性定理=A,这些都是非黑即 白的经典定理。) 模糊(矛盾)的产生,就是西方逻辑的结束 P(A⌒B) (2)是否可以推导条件概率算子P(B|A)= P(4) 经典集合论中P(A⌒A|AUA)=P(中|X)=0 (公理) 模糊理论:利用超集AUA是其子集A⌒A的子集程 度来衡量模糊集合A的模糊性,这是模糊集合的特有问题
考虑两个问题: (1) 总是真的吗?(模糊存在吗) 考虑是否逻辑上或实际中有违背“无矛盾定理”的现象 (Aristotle的三个‘思考定理’之一,另外两个是‘排中定 理’ ,‘同一性定理’ , 这些都是非黑即 白的经典定理。) 模糊(矛盾)的产生,就是西方逻辑的结束 (2)是否可以推导条件概率算子 ? 经典集合论中 (公理) 模糊理论:利用超集 是其子集 的子集程 度来衡量模糊集合A的模糊性,这是模糊集合的特有问题。 c A A = c A A X = A A = ( ) ( | ) ( ) P A B P B A P A = c A A c A A ( | ) ( | ) 0 c c P A A A A P X = =

2.随机与模糊:是否与多少 模糊是事件发生的程度。随机是事件是否发生的不确定性。 例子:明天有20%的几率下小雨(包含复合的不确定性) 冰箱里有一个苹果的概率为50%(Probability) 冰箱里有半个苹果(Fuzy) 停车位问题 模糊是一种确定的不定性(deterministic uncertainty),是物理 现象的特性。用模糊代表不确定性的结果将是震撼的,人们需 要重新审视现实模型
2. 随机与模糊:是否与多少 模糊是事件发生的程度。随机是事件是否发生的不确定性。 例子:明天有20%的几率下小雨(包含复合的不确定性) 冰箱里有一个苹果的概率为50%(Probability) 冰箱里有半个苹果(Fuzzy) 停车位问题 模糊是一种确定的不定性(deterministic uncertainty),是物理 现象的特性。用模糊代表不确定性的结果将是震撼的,人们需 要重新审视现实模型

不精确的椭圆 概率上的椭圆还是模糊的椭圆?没有随机性的问题,所以 属于模糊问题。可否m,(x)=Prob{x∈A)?概率并不能包 括所有的问题。概率论是一种有限测量理论。 修
不精确的椭圆 概率上的椭圆还是模糊的椭圆?没有随机性的问题,所以 属于模糊问题。可否 ?概率并不能包 括所有的问题。概率论是一种有限测量理论。 ( ) Pr { } m x ob x A A =

二、模糊集合的几何图示:sets as points 将论域X的所有模糊子集的集合一模糊幂集合F(2)看成一 个超立方体I”=[0,]”,将一个模糊集合看成是立方体内 的一个点。非模糊集对应立方体的顶点。中点离各顶点等 距,最大模糊。 也是唯一满足以下特性的点:A=A⌒A=AUA=A (多值连续集合理论) mAnB=min(mA,mg)) muB=maX(m4,mg)) m=1-ma
二、模糊集合的几何图示:sets as points 将论域X的所有模糊子集的集合——模糊幂集合 看成一 个超立方体 ,将一个模糊集合看成是立方体内 的一个点。非模糊集对应立方体的顶点。中点离各顶点等 距,最大模糊。 也是唯一满足以下特性的点: (多值连续集合理论) (2 ) X F [0,1] n n I = c c c A A A A A A = = = min( , ) max( , ) c 1 A B A B A B A B A A m m m m m m m m = = = −
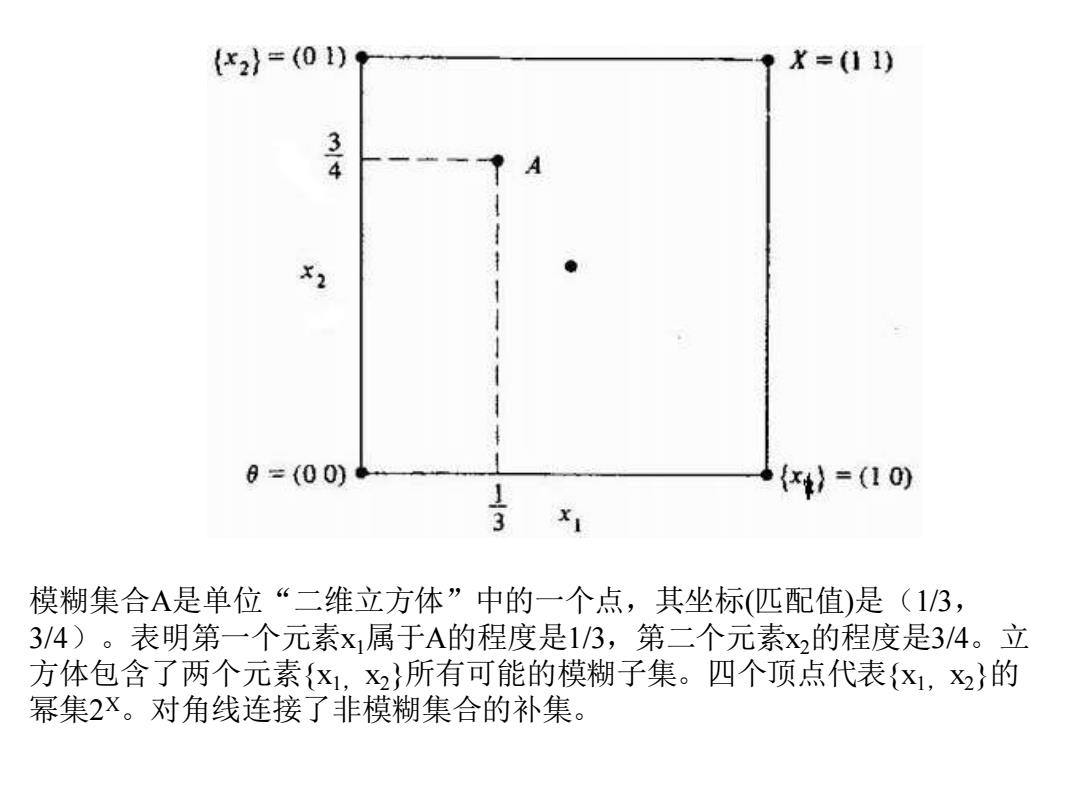
{x2}=(01) X=(11) A X2 ● 6=(00) {}=(10) 13 模糊集合A是单位“二维立方体”中的一个点,其坐标(匹配值)是(1/3, 3/4)。表明第一个元素x1属于A的程度是1/3,第二个元素x2的程度是3/4。立 方体包含了两个元素{x1,x2}所有可能的模糊子集。四个顶点代表{X1,X2}的 幂集2x。对角线连接了非模糊集合的补集
模糊集合A是单位“二维立方体”中的一个点,其坐标(匹配值)是(1/3, 3/4)。表明第一个元素x1属于A的程度是1/3,第二个元素x2的程度是3/4。立 方体包含了两个元素{x1,x2}所有可能的模糊子集。四个顶点代表{x1,x2}的 幂集2 X。对角线连接了非模糊集合的补集
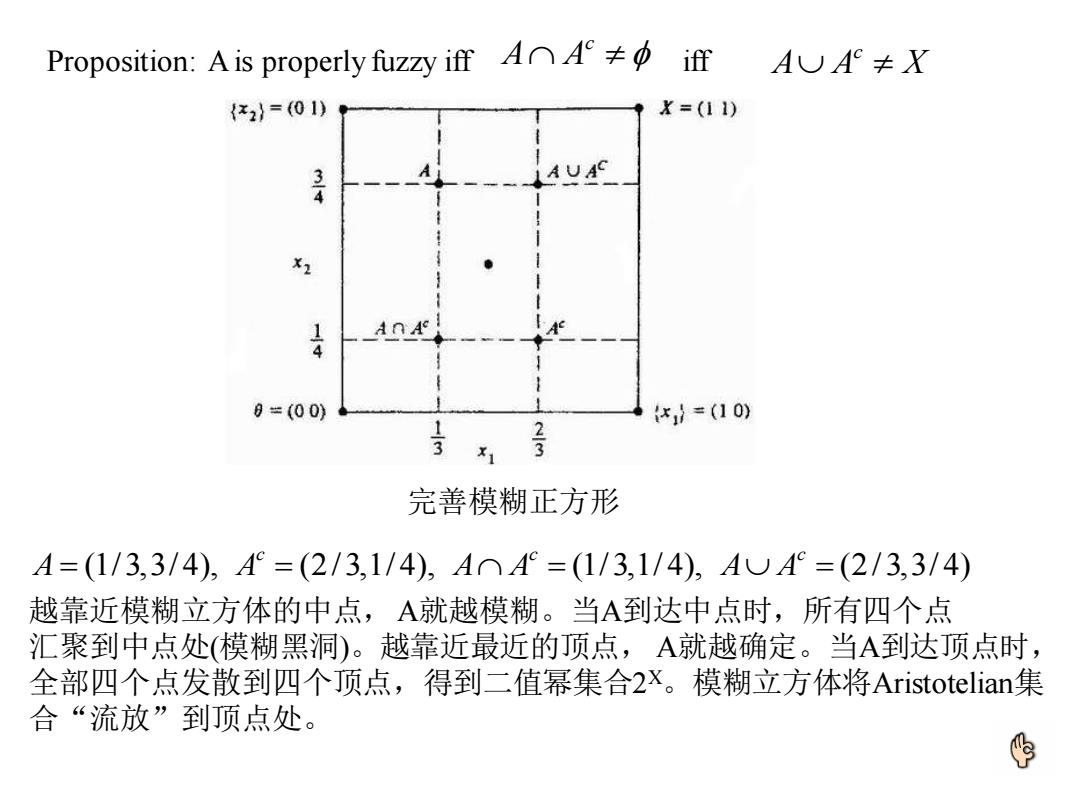
Proposition:A is properly fuzzy iff A∩A≠中if AUA°≠X {x2}=(01) X=(11) UA AnA 8=(00) }=(10) 23 完善模糊正方形 A=(1/3,3/4),A=(2/3,1/4),A⌒A=(1/3,1/4),AUA=(2/3,3/4) 越靠近模糊立方体的中点,A就越模糊。当A到达中点时,所有四个点 汇聚到中点处(模糊黑洞)。越靠近最近的顶点,A就越确定。当A到达顶点时, 全部四个点发散到四个顶点,得到二值幂集合2x。模糊立方体将Aristotelian集 合“流放”到顶点处
越靠近模糊立方体的中点,A就越模糊。当A到达中点时,所有四个点 汇聚到中点处(模糊黑洞)。越靠近最近的顶点, A就越确定。当A到达顶点时, 全部四个点发散到四个顶点,得到二值幂集合2 X。模糊立方体将Aristotelian集 合“流放”到顶点处。 Proposition: A is properly fuzzy iff iff c A A X c A A (1/ 3,3/ 4), (2/ 3,1/ 4), (1/ 3,1/ 4), (2/ 3,3/ 4) c c c A A A A A A = = = = 完善模糊正方形
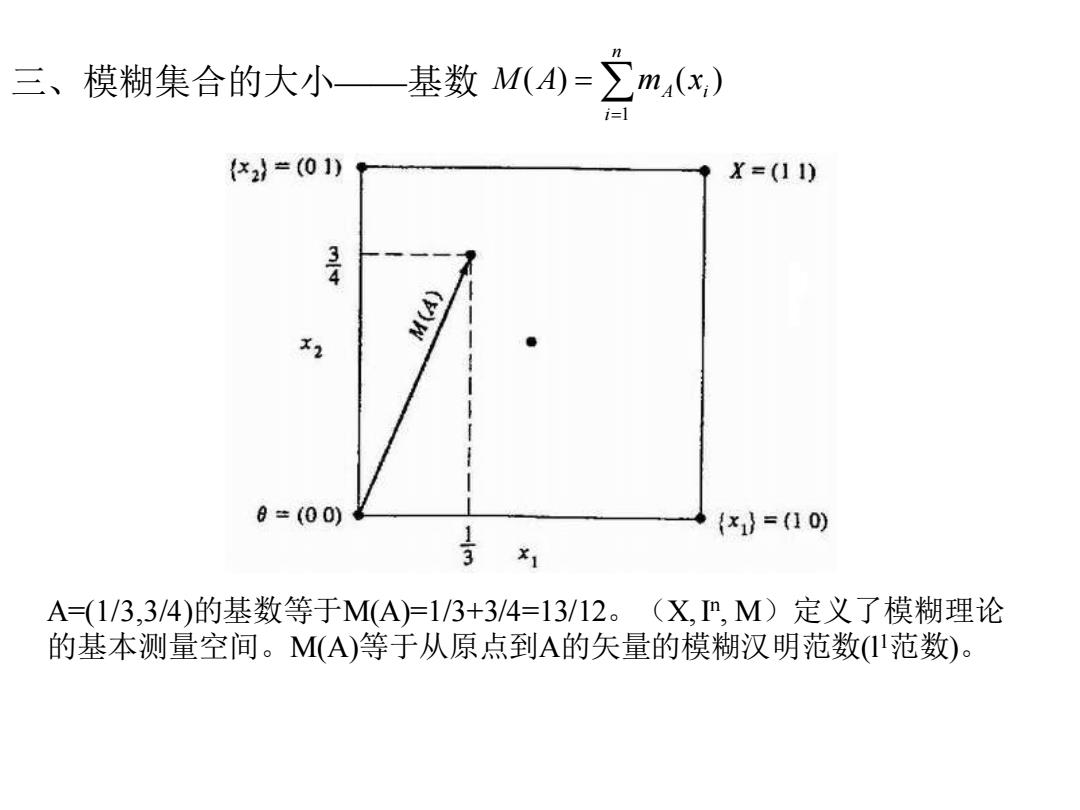
三、模糊集合的大小一基数M(4)=∑m(x,) {2}=(01) X=(11) X2 8=(00) {x}=(10) X1 A=(1/3,3/4)的基数等于M(A)=1/3+3/4=13/12。(X,m,M)定义了模糊理论 的基本测量空间。M(A)等于从原点到A的矢量的模糊汉明范数I范数)
三、模糊集合的大小——基数 1 ( ) ( ) n A i i M A m x = = A=(1/3,3/4)的基数等于M(A)=1/3+3/4=13/12。(X, In , M)定义了模糊理论 的基本测量空间。M(A)等于从原点到A的矢量的模糊汉明范数(l1范数)