
模糊与卡尔曼滤波目标跟踪控制系统的比较 Comparison of Fuzzy and Kalman-Filter Target-Tracking control system Peter J.Pacini,Bart Kosko 报告人:宋骊平
模糊与卡尔曼滤波目标跟踪控制系统的比较 Comparison of Fuzzy and Kalman-Filter Target-Tracking control system 报告人:宋骊平 Peter J.Pacini , Bart Kosko

内容简个 1、模糊控制器与卡尔曼滤波器的比拉 2、实时目标跟踪系统 3、模糊控制器的工作原理 4、卡尔曼跟踪与模糊跟踪伤真 5、面适应FAM
1、模糊控制器与卡尔曼滤波器的比较 3、模糊控制器的工作原理 2、实时目标跟踪系统 内容简介 5、自适应FAM 4、卡尔曼跟踪与模糊跟踪仿真
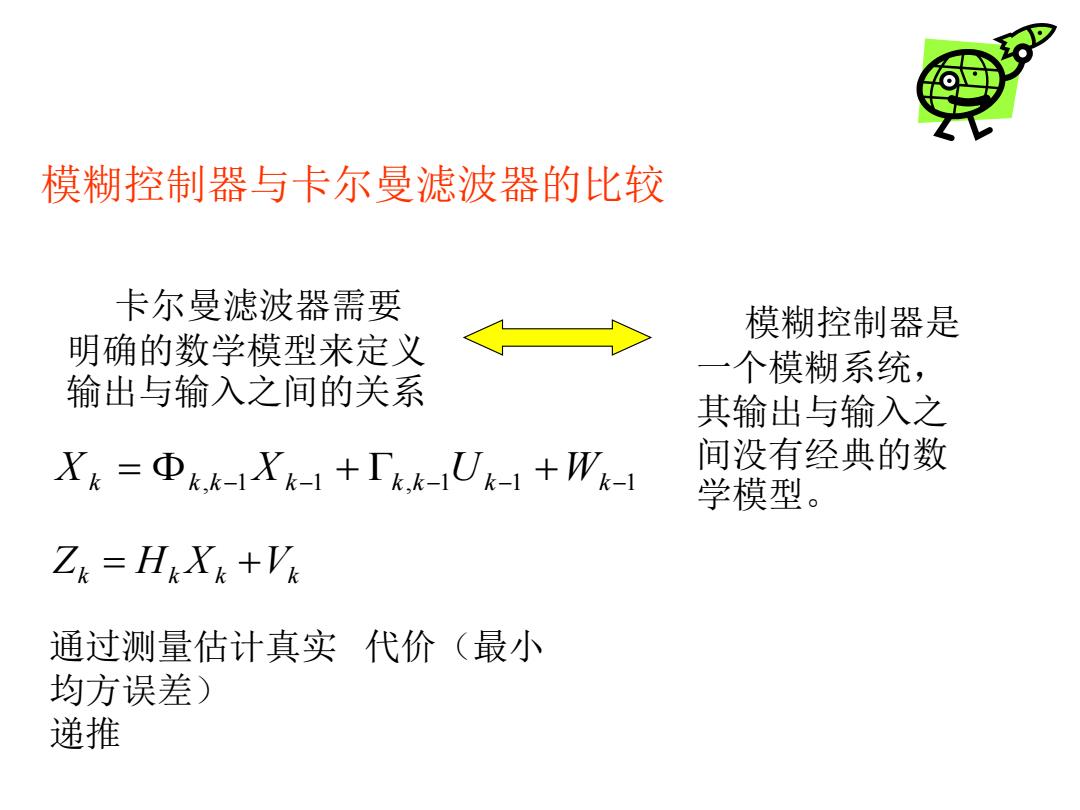
模糊控制器与卡尔曼滤波器的比较 卡尔曼滤波器需要 模糊控制器是 明确的数学模型来定义 一个模糊系统, 输出与输入之间的关系 其输出与输入之 Xk=Φkk-1Xk-1+「kk-Uk-1+Wk-l 间没有经典的数 学模型。 ZR=HkXk +VR 通过测量估计真实代价(最小 均方误差) 递推
模糊控制器与卡尔曼滤波器的比较 卡尔曼滤波器需要 明确的数学模型来定义 输出与输入之间的关系 模糊控制器是 一个模糊系统, 其输出与输入之 间没有经典的数 , −1 −1 , −1 −1 −1 学模型。 Xk = k k Xk + k k Uk +Wk Zk = Hk Xk +Vk 通过测量估计真实 代价(最小 均方误差) 递推

数学模型控制器的问题 数学模型控制器在输出和输入的函数关系确定的情况下的 工作性能会很好。对于不确定的环境,数学模型控制器一般 采用概率分布来描述。存在以下问题: (1)不确定性一般很难用经典数据模型加以准确描述。 (2)很难将专家的知识加到系统中去,在这种系统中, 专家的知识一般只能用来估计初始状态和协方差条件
数学模型控制器的问题 数学模型控制器在输出和输入的函数关系确定的情况下的 工作性能会很好。对于不确定的环境,数学模型控制器一般 采用概率分布来描述。存在以下问题: (1)不确定性一般很难用经典数据模型加以准确描述。 (2)很难将专家的知识加到系统中去,在这种系统中, 专家的知识一般只能用来估计初始状态和协方差条件

实时目标跟踪系统 实时目标跟踪系统一般采用雷达或其它设备去探测目标与设备所 在平面的的高度和方位角。由两个马达控制设备的探测方向,通过连 续地调整两个马达的转速,保持对目标的连续跟踪。 对高度和方位角的控制可以采用相同的算法进行
实时目标跟踪系统 实时目标跟踪系统一般采用雷达或其它设备去探测目标与设备所 在平面的的高度和方位角。由两个马达控制设备的探测方向,通过连 续地调整两个马达的转速,保持对目标的连续跟踪。 对高度和方位角的控制可以采用相同的算法进行
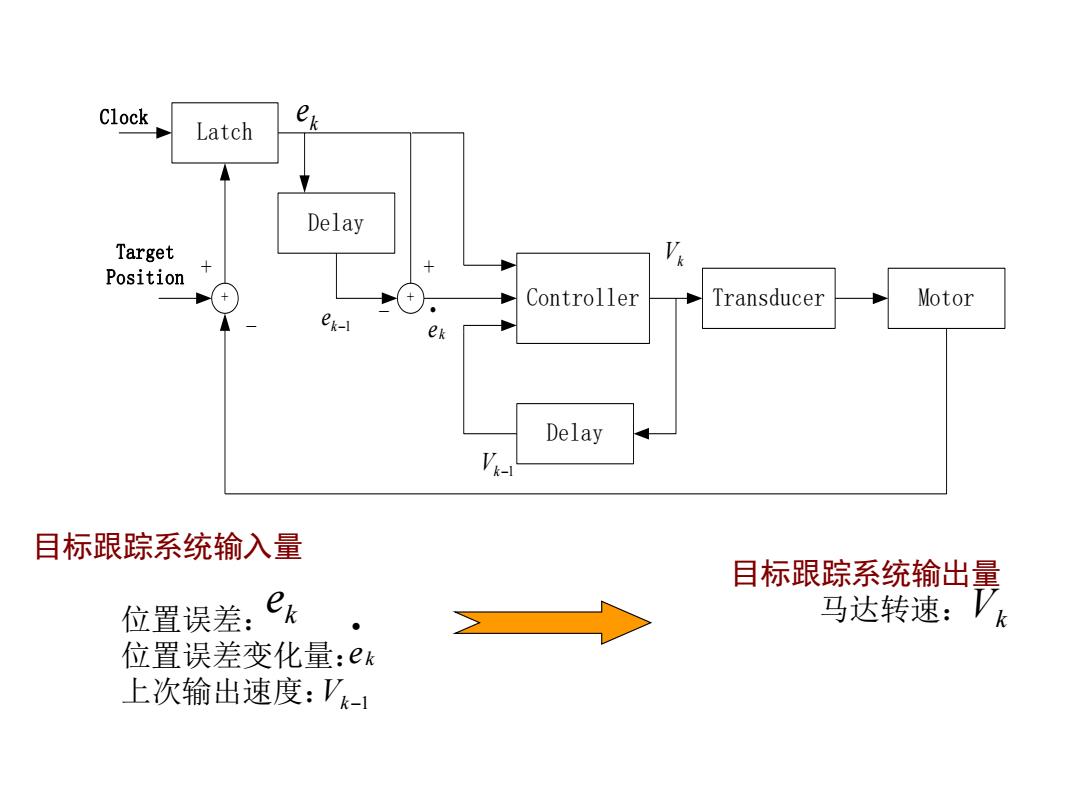
Clock Latch Delay Target Position Controller Transducer Motor ek Delay V 目标跟踪系统输入量 目标跟踪系统输出量 位置误差:ek 马达转速:Vk 位置误差变化量:ek 上次输出速度:Vk-
目标跟踪系统输入量 位置误差: 位置误差变化量: 上次输出速度: 目标跟踪系统输出量 e k 马达转速: e k • Vk − 1 Vk Latch Delay Controller Delay + + Transducer Motor Clock Target Position + - k e ek • Vk−1 Vk k−1 e + -
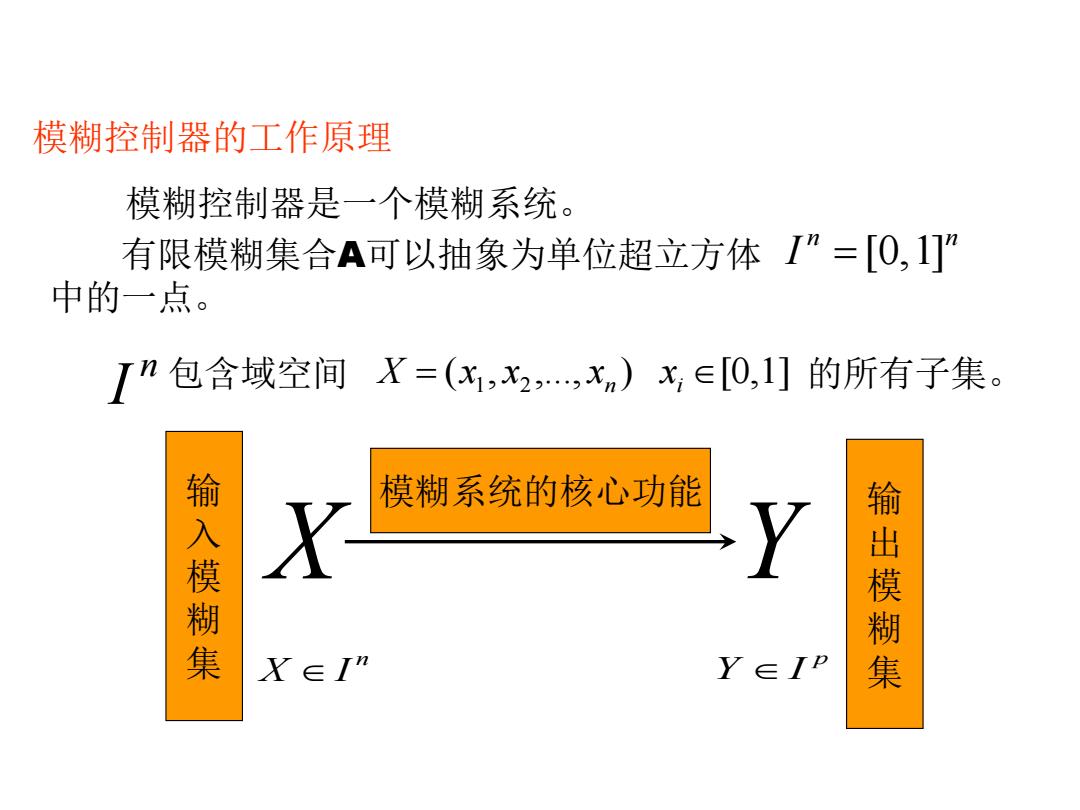
模糊控制器的工作原理 模糊控制器是一个模糊系统。 有限模糊集合A可以抽象为单位超立方体I”=[O,] 中的一点。 In包含域空间X=(x,2,,x)x,∈[0,1]的所有子集。 模糊系统的核心功能 输入模糊集 输出模糊集 X∈I” Y∈IP
模糊控制器的工作原理 有限模糊集合A可以抽象为单位超立方体 中的一点。 ( , ,..., ) [0,1] X = x1 x2 xn xi n n I = [0,1] n I 模糊控制器是一个模糊系统。 包含域空间 的所有子集。 X Y n X I p Y I 输 模糊系统的核心功能 入 模 糊 集 输 出 模 糊 集

模拟输 FAM规则1 e 入量 模拟输 出量 模糊化 FAM规则2 解模糊 FAM规则n 延迟 模糊控制器的结构框图
模糊化 解模糊 模拟输 入量 FAM规则1 FAM规则2 FAM规则n ... 模拟输 出量 O1 O2 On O k v 延迟 模糊控制器的结构框图

(1)输入量的模糊化 -6 LN:Large Negative -4 MN:Medium Negative -2 SN:Small Negative 输出角速度:【-6,6] 0 ZE:Zero 2 SP:Small Positive 4 MP:Medium Positive 6 LP:Large Positive 给定一个输入量,将其归入(一6,6)区间后,可以用某 些特定的函数计算其属于某个集合的隶属度
(1)输入量的模糊化 输出角速度:[-6,6] -6 LN: Large Negative MN: Medium Negative SN: Small Negative ZE: Zero SP: Small Positive MP: Medium Positive LP: Large Positive -4 -2 0 2 4 6 给定一个输入量,将其归入(-6,6)区间后,可以用某 些特定的函数计算其属于某个集合的隶属度
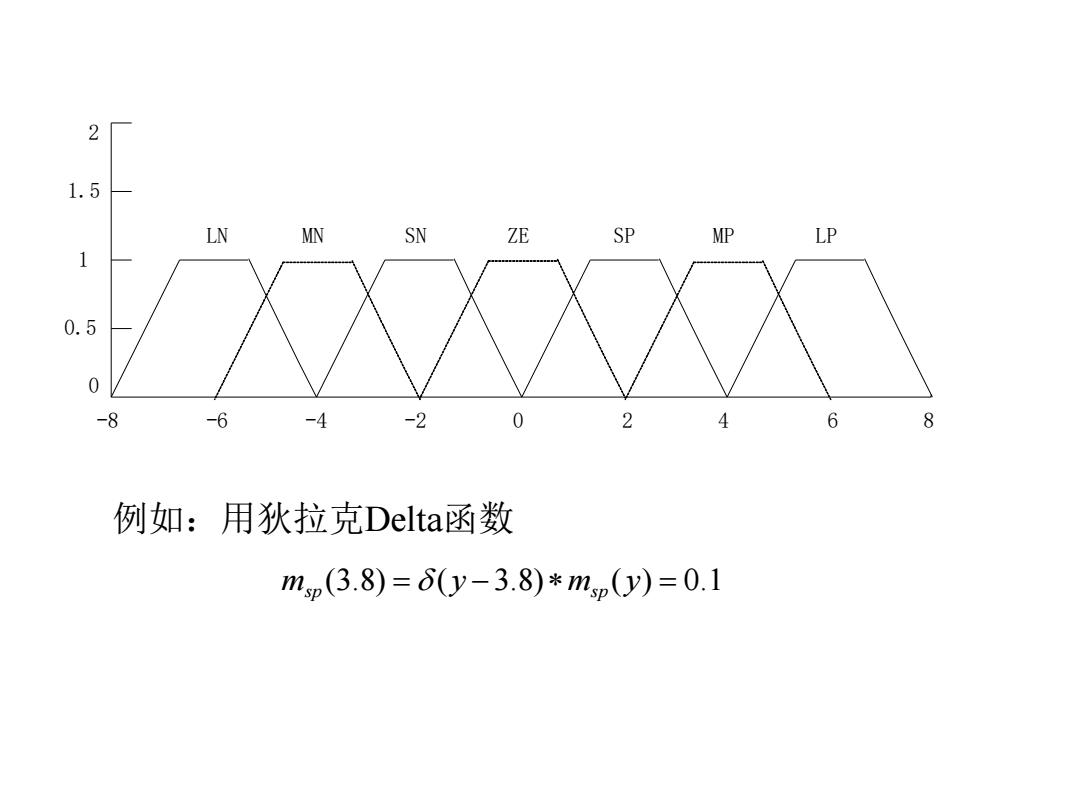
2 1.5 LN MN SN ZE SP MP LP 1 0.5 0 -8 -6 -4 -2 0 2 4 6 8 例如:用狄拉克Delta函数 mp(3.8)=6(y-3.8)*mp(y)=0.1
0 0.5 1 1.5 2 -8 -6 -4 -2 0 2 4 6 8 LN MN SN ZE SP MP LP 例如:用狄拉克Delta函数 ms p (3.8) = ( y −3.8)ms p ( y) = 0.1