
第五章突触动力学川:有监督学习 王衡
第五章 突触动力学Ⅱ:有监督学习 王衡

目录 1有监督的函数估计 冬2有监督的学习相当于操作性条件反射 3有监督的学习相当于有先验知识的随机模式 学习 4算法,感知器,LMS,BP
目录 ❖ 1有监督的函数估计 ❖ 2有监督的学习相当于操作性条件反射 ❖ 3有监督的学习相当于有先验知识的随机模式 学习 ❖ 4算法,感知器,LMS,BP

1.有监督的函数估计 冬给定观察得到的随机矢量样本对: (x,y),(x2,2),…(xm,ym) 要估计一个未知函数:f:x一y,并且使期望 误差函数EJ]最小。误差=期望输出-实际输 出
1.有监督的函数估计 ❖ 给定观察得到的随机矢量样本对: 要估计一个未知函数:f : x—y,并且使期望 误差函数E[J]最小。误差=期望输出-实际输 出 1 1 2 2 ( , ), ( , ), ( , ) m m x y x y x y

1.有监督的丞数估计 冬设N为一个神经网络的传递函数,那么可以定义 瞬时误差为y一N(x),这是一个随机向量, 因为我们不知道联合概率密度函数p(仪,y),所以, 无法求出, E[y,-N(用 E[(y:-W(x)(y,-Nx,逼近用观测到的 随机量来估计期望值,然后在离散的近似算法中 使用这些估计量,通常是随机的梯度下降法,举 个例子,在Vidrow's LMS算法中,他用的梯度 是随机梯度
1.有监督的函数估计 ❖ 设N为一个神经网络的传递函数,那么可以定义 瞬时误差为 ,这是一个随机向量, 因为我们不知道联合概率密度函数p(x,y),所以, 无法求出, 一般用 。随机逼近用观测到的 随机量来估计期望值,然后在离散的近似算法中 使用这些估计量,通常是随机的梯度下降法,举 个例子,在Widrow’s LMS算法中,他用的梯度 是随机梯度 ( ) i i y N x − [ ( )] E y N x i i − [( ( ))( ( )) ] T E y N x y N x i i i i − −

理解细节 1.error surface 2.m* 3.函数估计与分类
理解细节 ❖ 1.error surface ❖ 2.m* ❖ 3.函数估计与分类
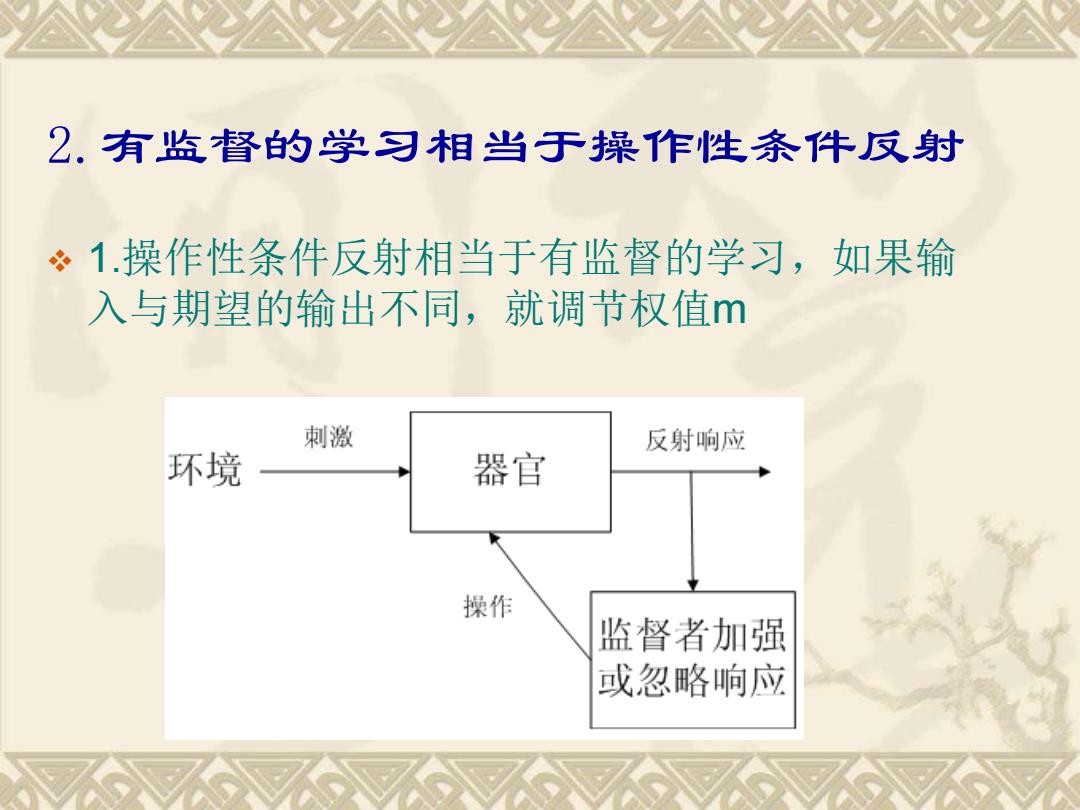
2.有监督的学习相当于操作性条件反射 。1.操作性条件反射相当于有监督的学习,如果输 入与期望的输出不同,就调节权值m 刺激 反射响应 环境 器官 操作 监督者加强 或忽略响应
2.有监督的学习相当于操作性条件反射 ❖ 1.操作性条件反射相当于有监督的学习,如果输 入与期望的输出不同,就调节权值m
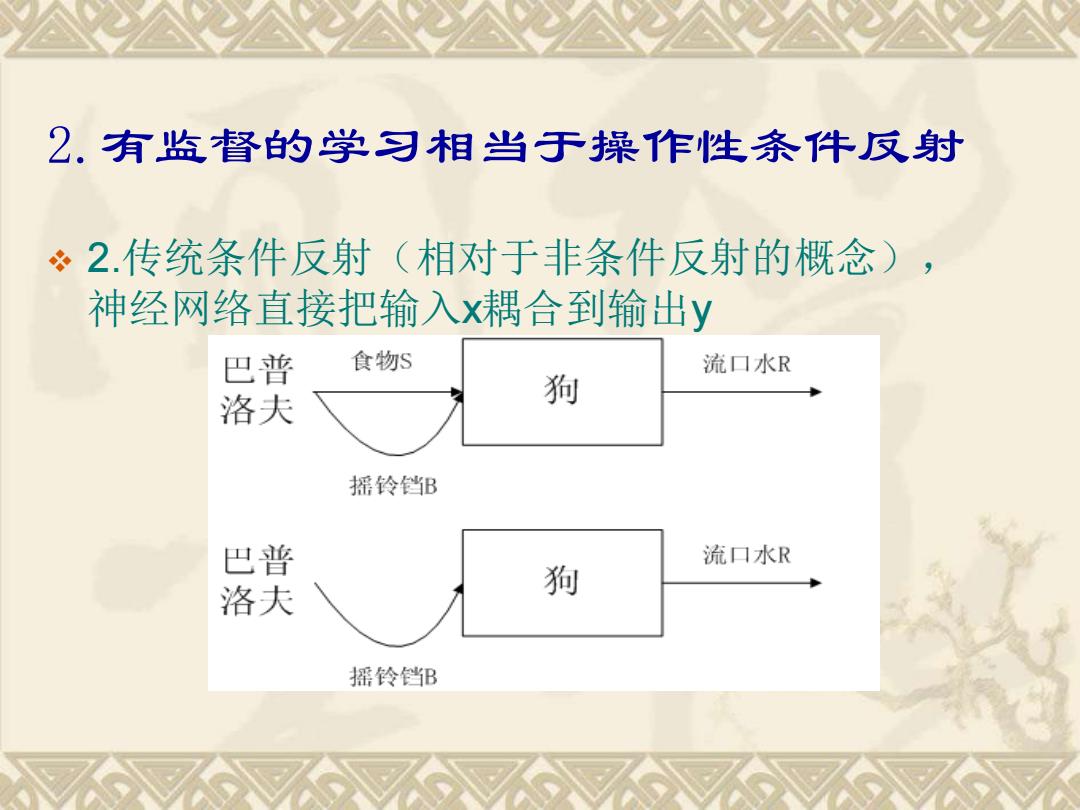
2.有监督的学习相当于操作性条件反射 2.传统条件反射(相对于非条件反射的概念), 神经网络直接把输入x耦合到输出y 巴普 食物S 流口水R 洛夫 狗 摇铃铛B 巴普 流口水R 洛夫 狗 摇铃铛B
2.有监督的学习相当于操作性条件反射 ❖ 2.传统条件反射(相对于非条件反射的概念), 神经网络直接把输入x耦合到输出y

2.有监督的学习相当于操作性条件反射 ÷操作性条件反射的例子 1自然选择 2家长教育孩子 传统条件反射的例子 1巴普洛夫试验 2望梅止渴
2.有监督的学习相当于操作性条件反射 ❖ 操作性条件反射的例子 1自然选择 2家长教育孩子 ❖ 传统条件反射的例子 1巴普洛夫试验 2望梅止渴

3,有监督的学习相当于有先验知识的随机模式 学习 1.模式 模式就是特征域”上的一个点,随机时变模式 定义了一个随机过程x),t属于[0,T],值域是 特征域R” ÷2.随机模式学习 由已知的样本x1),x(2)..x)来估计x的概率 密度函数p(
3.有监督的学习相当于有先验知识的随机模式 学习 ❖ 1.模式 模式就是特征域 上的一个点,随机时变模式 定义了一个随机过程x(t),t属于[0,T],值域是 特征域 ❖ 2.随机模式学习 由已知的样本x(1),x(2)…x(n)来估计x的概率 密度函数p(x) n R n R

3.有监督的学习相当于有先验知识的随机模式 学习 ÷3.类 R”的子集,下面假设我们把模式空间 分成了 k个不相交的子集DD,也叫决策类 R”=DUD2UD且D∩D,=Φ如果i≠j 4.类的概率 P(D)-p()d=[()(ds
3.有监督的学习相当于有先验知识的随机模式 学习 ❖ 3.类 的子集,下面假设我们把模式空间 分成了 k个不相交的子集 D D 1 ... k ,也叫决策类 ❖ 4.类的概率 n R 1 2 n R D D D D D i j = = k i j 且 如果 ( ) ( ) ( ) ( ) [ ( )] i i n i i D D D R P D p x dx I x p x dx E I x = = =