
NEURAL NETWORK THEORY NEURAL DYNAMIC1: ACTIVATIONHS AND SIGNALS
NEURAL NETWORK THEORY NEURAL DYNAMIC1: ACTIVATIONHS AND SIGNALS

MAIN POINTS: NEURONS AS FUNCTIONS(神经元函数) SIGNAL MONOTONICITY(信号单调性) BIOLOGICAL ACTIVATIONS AND SIGNALS(生物激 励与信号) NEURON FIELDS(神经域 NEURONAL DYNAMICAL SYSTEMS(神经诊断系统) COMMON SIGNAL FUNCTION(一般信号方程) PULSE-CODED SIGNAL FUNCTION(脉冲编码信号 方程)
MAIN POINTS: • NEURONS AS FUNCTIONS(神经元函数) • SIGNAL MONOTONICITY(信号单调性) • BIOLOGICAL ACTIVATIONS AND SIGNALS(生物激 励与信号) • NEURON FIELDS(神经域) • NEURONAL DYNAMICAL SYSTEMS(神经诊断系统) • COMMON SIGNAL FUNCTION(一般信号方程) • PULSE-CODED SIGNAL FUNCTION(脉冲编码信号 方程)
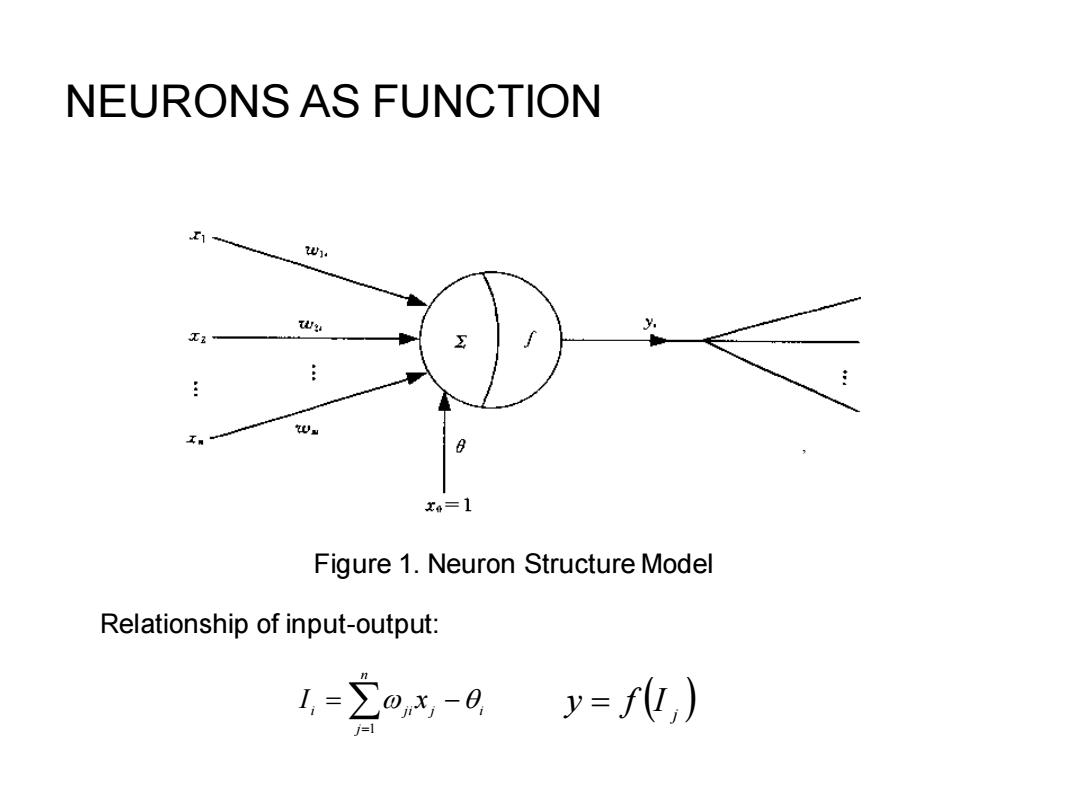
NEURONS AS FUNCTION w Wy x6=1 Figure 1.Neuron Structure Model Relationship of input-output: 1,=2o,x-日y=f,)
NEURONS AS FUNCTION Figure 1. Neuron Structure Model j i n j i ji I = x − =1 ( )j y = f I , Relationship of input-output:

NEURONS AS FUNCTION .Common nonlinear transduction description:a sigmoidal or S-shaped curve s(x) c=5.0 1.0 c=2.0 c=0.2 0 x Fig.2 s(x)is a bounded monotone-nondecreasing function of x Signal Function:S(x)= 1tea dS =cS(1-S)>0 dx (c>0) Neurons transduce an unbounded input activation x(t)at time t into a bounded output signal S(x(t))
•Common nonlinear transduction description: a sigmoidal or S-shaped curve Fig.2 s(x) is a bounded monotone-nondecreasing function of x Signal Function: cx e S x − + = 1 1 ( ) ' = = cS(1− S) 0 (c 0) dx dS S Neurons transduce an unbounded input activation x(t) at time t into a bounded output signal S(x(t)). NEURONS AS FUNCTION

SIGNAL MONOTONICITY In general,signal functions are monotone nondecreasing S'>=0.In practice this means signal functions have an upper bound or saturation value An important exception:bell-shaped signal function or Gaussian signal functions S(x)=e-r c>0 S=-2cxe S"oc-x The sign of the signal-activation derivation s'is opposite the sign of the activation x.We shall assume signal functions are monotone nondecreasing unless stated otherwise
SIGNAL MONOTONICITY ( ) 0 2 = − S x e c cx • In general, signal functions are monotone nondecreasing S’>=0. In practice this means signal functions have an upper bound or saturation value. • An important exception: bell-shaped signal function or Gaussian signal functions S cxe S x cx = − − − ' 2 , ' 2 The sign of the signal-activation derivation s’ is opposite the sign of the activation x. We shall assume signal functions are monotone nondecreasing unless stated otherwise

SIGNAL MONOTONICITY .Generalized Gaussian signal function define potential or radial basis function: x)x-] input activation vector: x=(X1,…,xn)∈R variance: o mean vector: 4,=(4,…,4) Because the function depend on all neuronal activations not just the ith activation,we shall consider only scalar-input signal functions.S(x
SIGNAL MONOTONICITY ( ) ] 2 1 ( ) exp[ 2 = − 2 − n j i j j i i S x x 2 i : •Generalized Gaussian signal function define potential or radial basis function: n input activation vector: x = (x1 , , x n ) R mean vector: ( , , ) 1 i n i i = ( ) i i S x Because the function depend on all neuronal activations not just the ith activation, we shall consider only scalar-input signal functions:

SIGNAL MONOTONICITY A property of signal monotonicity:semi-linearity 、Comparation: a.Linear signal functions: computation and analysis is comparatively easy;do not suppress noise. b.Nonlinear signal functions: Increases a network's computational richness and facilitates noise suppression;risks computational and analytical intractability;
SIGNAL MONOTONICITY • A property of signal monotonicity: semi-linearity • Comparation: a. Linear signal functions: computation and analysis is comparatively easy; do not suppress noise. b. Nonlinear signal functions: Increases a network’s computational richness and facilitates noise suppression; risks computational and analytical intractability;

SIGNAL MONOTONICITY .Signal and activation velocities the signal velocity: S=dS/dt S= dS dx dx dt -Sx Signal velocities depend explicitly on action velocities.This dependence will increase the number of unsupervised learning laws
SIGNAL MONOTONICITY S x dt dx dx dS S = = ' •Signal and activation velocities the signal velocity: =dS/dt S Signal velocities depend explicitly on action velocities. This dependence will increase the number of unsupervised learning laws

BIOLOGICAL ACTIVATIONS AND SIGNALS .Introduction to units 细胞体(soma) Dendrite:input 树突(dendrites) Axon:output Synapse:transduce signal 轴突(aRon) 突触(synapse Membrane:potential difference between inside and outside of neuron Fig3.Key functional units of a biological neuron
BIOLOGICAL ACTIVATIONS AND SIGNALS Fig3. Key functional units of a biological neuron •Introduction to units : Dendrite: input Axon: output Synapse: transduce signal Membrane: potential difference between inside and outside of neuron

BIOLOGICAL ACTIATIONS AND SIGNALS .Competitive Neuronal Signal Signal values are usually binary and bipolar. Binary signal functions: -o x>T X≤I Bipolar signal functions x >T x≤T
BIOLOGICAL ACTIVATIONS AND SIGNALS •Competitive Neuronal Signal Signal values are usually binary and bipolar. Bipolar signal functions : Binary signal functions : ( ) = x T x T s x 0 1 ( ) − = x T x T s x 1 1