
NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS NEURONS AS FUNCTIONS Neurons behave as functions. Neurons transduce an unbounded input activation x(t)at time t into a bounded output signal S(x(t)). 2
2 NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURONS AS FUNCTIONS Neurons behave as functions. Neurons transduce an unbounded input activation x(t) at time t into a bounded output signal S(x(t))

NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS NEURONS AS FUNCTIONS The transduction description:a sigmoidal or S-shaped curve the logistic signal function: S(x)= +e-a =eS(1-S)>0 (c>0) dx The logistic signal function is sigmoidal and strictly increases for positive scaling constant c>0. 3
3 NEURONS AS FUNCTIONS The transduction description: a sigmoidal or S-shaped curve the logistic signal function: cx e S x − + = 1 1 ( ) ' = = cS(1− S) 0 (c 0) dx dS S The logistic signal function is sigmoidal and strictly increases for positive scaling constant c >0. NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS
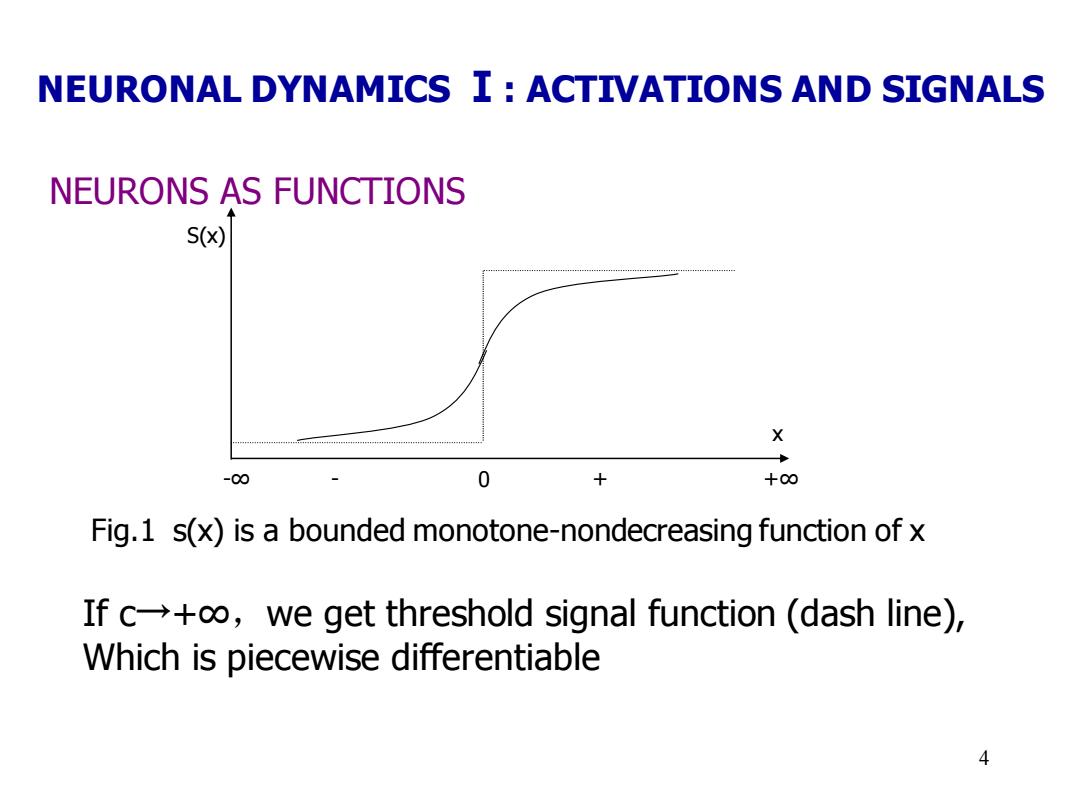
NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS NEURONS AS FUNCTIONS S(x) X -00 0 +00 Fig.1 s(x)is a bounded monotone-nondecreasing function of x If c+o,we get threshold signal function (dash line), Which is piecewise differentiable 4
4 NEURONS AS FUNCTIONS S(x) x -∞ - 0 + +∞ Fig.1 s(x) is a bounded monotone-nondecreasing function of x If c→+∞,we get threshold signal function (dash line), Which is piecewise differentiable NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS

NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY In general,signal functions are monotone nondecreasing S'>=0.This means signal functions have an upper bound or saturation value. The staircase signal function is a piecewise-differentiable Monotone-nondecreasing signal function. 5
5 SIGNAL MONOTONICITY In general, signal functions are monotone nondecreasing S’>=0. This means signal functions have an upper bound or saturation value. The staircase signal function is a piecewise-differentiable Monotone-nondecreasing signal function. NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS

NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY An important exception:bell-shaped signal function or Gaussian signal functions S(x)=e-cx c>0 S=-2cxe S S"o∝-x The sign of the signal-activation derivation s'is opposite the sign of the activation x.We shall assume signal functions are monotone nondecreasing unless stated otherwise. 6
6 SIGNAL MONOTONICITY An important exception: bell-shaped signal function or Gaussian signal functions 0 2 = − S x e c cx ( ) S cxe S x cx = − − − ' 2 , ' 2 The sign of the signal-activation derivation s’ is opposite the sign of the activation x. We shall assume signal functions are monotone nondecreasing unless stated otherwise. NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS

NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY Generalized Gaussian signal function define potential or radial basis function S (x): s=6p22x,-41 input activation vector:x=(xi,…,xn)∈R" variance:o, mean vector:=() we shall consider only scalar-input signal functions:S (x 7
7 SIGNAL MONOTONICITY Generalized Gaussian signal function define potential or radial basis function : ( ) ] 2 1 ( ) exp[ 2 = − 2 − n j i j j i i S x x n x = (x1 , , xn )R ( , , ) i n i i = 1 input activation vector: variance: mean vector: NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS 2 i S (x) i we shall consider only scalar-input signal functions: ( ) i i S x

NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY neurons are nonlinear but not too much so----a property as semilinearity Linear signal functions make computation and analysis comparatively easy - do not suppress noise linear network are not robust Nonlinear signal functions increases a network's computational richness increases a network's facilitates noise suppression risks computational and analytical intractability favors dynamical instability 8
8 SIGNAL MONOTONICITY neurons are nonlinear but not too much so ---- a property as semilinearity Linear signal functions - make computation and analysis comparatively easy - do not suppress noise - linear network are not robust Nonlinear signal functions - increases a network’s computational richness - increases a network’s facilitates noise suppression - risks computational and analytical intractability - favors dynamical instability NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS

NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY Signal and activation velocities the signal velocity:S =dS/dt 5= dS dx dx dt -Sx Signal velocities depend explicitly on action velocities 9
9 SIGNAL MONOTONICITY Signal and activation velocities the signal velocity: =dS/dt Signal velocities depend explicitly on action velocities S S x dt dx dx dS S = = ' NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS

NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS BIOLOGICAL ACTIVATIONS AND SIGNALS 来自其他神经轴 突的神经末梢 神经末梢 树突 细胞体 轴突 突触 生物神经元 Fig.2 Neuron anatomy 神经元(Neuron)是由细胞核(cell nucleus),细胞体(soma),轴 突(axon),树突(dendrites)和突触(synapse)所构成的 10
10 BIOLOGICAL ACTIVATIONS AND SIGNALS Fig.2 Neuron anatomy 神经元(Neuron)是由细胞核(cell nucleus),细胞体(soma),轴 突(axon),树突(dendrites)和突触(synapse)所构成的 NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS
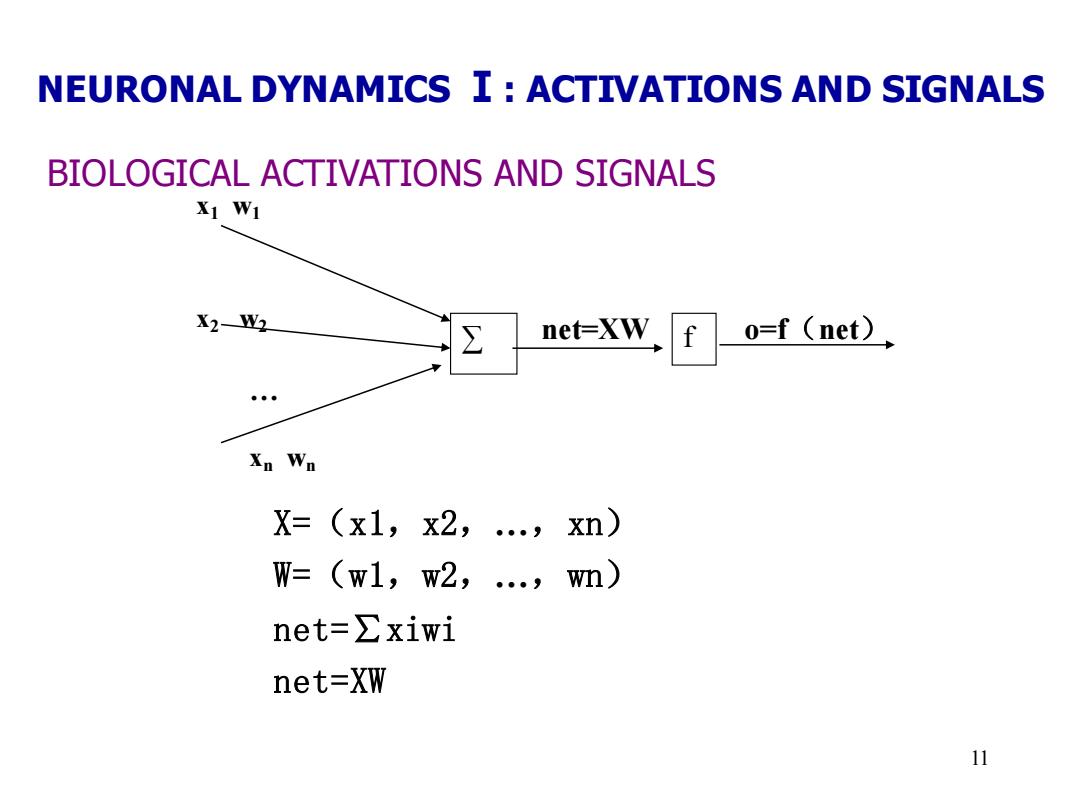
NEURONAL DYNAMICS I:ACTIVATIONS AND SIGNALS BIOLOGICAL ACTIVATIONS AND SIGNALS X1 W1 X2-W2 net=XW f o=f (net), Xn Wn X=(x1,x2,.,xn) W=(w1,w2,..,wn) net=∑xiwi net-XW 11
11 X=(x1,x2,…,xn) W=(w1,w2,…,wn) net=∑xiwi net=XW x2 w2 ∑ f o=f(net) xn wn … net=XW x1 w1 BIOLOGICAL ACTIVATIONS AND SIGNALS NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS