
Soft Computing integrating Evolutionary Neural and Fuzzy Systeme Neuro-fuzzy Systems Xinbo Gao School of Electronic Engineering Xidian University 2004,10
Neuro-fuzzy Systems Xinbo Gao School of Electronic Engineering Xidian University 2004,10

Introduction Neuro-fuzzy systems Soft computing methods that combine in various ways neural networks and fuzzy concepts ANN-nervous system -low level perceptive and signal integration Fuzzy part-represents the emergent higher level"reasoning aspects
Introduction ◼ Neuro-fuzzy systems ◼ Soft computing methods that combine in various ways neural networks and fuzzy concepts ◼ ANN – nervous system – low level perceptive and signal integration ◼ Fuzzy part – represents the emergent “higher level” reasoning aspects
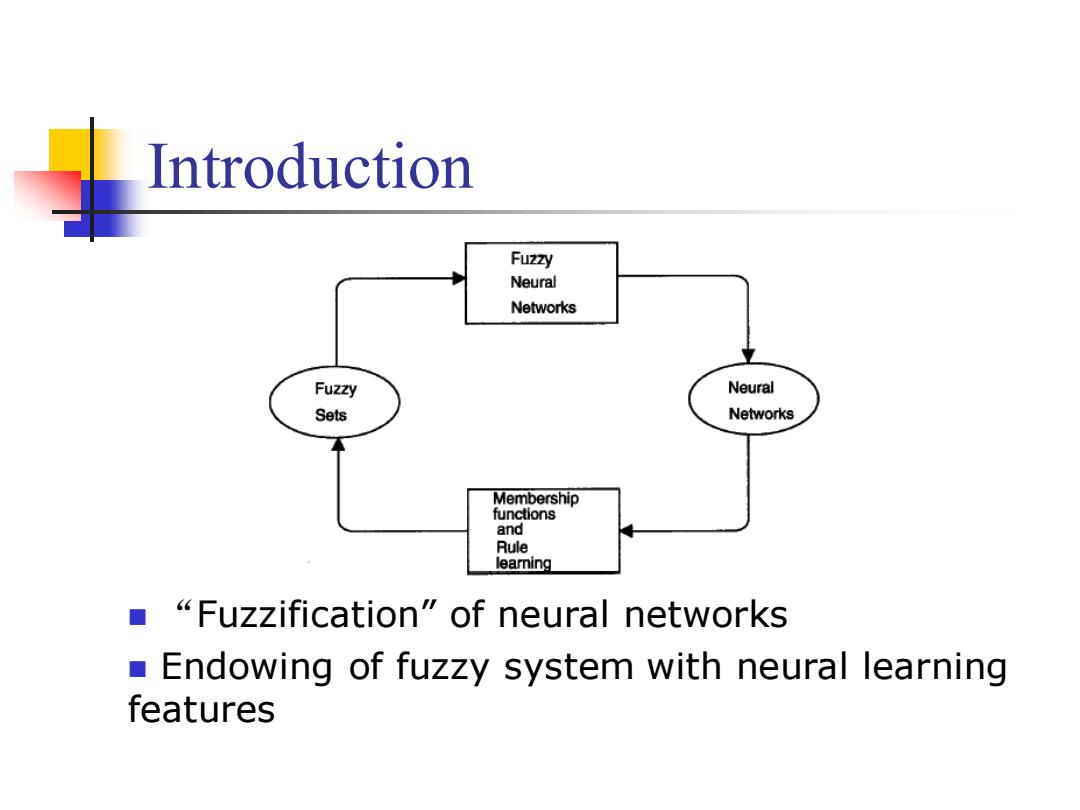
Introduction Fuzzy Neural Networks Fuzzy Neural Sets Networks Membership functions and Rule learning ■“Fuzzification"of neural networks Endowing of fuzzy system with neural learning features
Introduction ◼ “Fuzzification” of neural networks ◼ Endowing of fuzzy system with neural learning features

Introduction Co-operative-neural algorithm adapt fuzzy systems Off-line -adaptation On-line-algorithms are used to adapt as the system operates ■( Concurrent -where the two techniques are applied after one another as pre-or post-processing Hybrid-fuzzy system being representedas a network structure, making it possible to take advantage of learning algorithm inherited from ANNs
Introduction ◼ Co-operative-neural algorithm adapt fuzzy systems ◼ Off-line – adaptation ◼ On-line – algorithms are used to adapt as the system operates ◼ Concurrent – where the two techniques are applied after one another as pre- or post-processing ◼ Hybrid – fuzzy system being represented as a network structure, making it possible to take advantage of learning algorithm inherited from ANNs

Fuzzy Neural Networks Introduction of fuzzy concepts into artificial neurons and neural networks For example,while neural networks are good at recognizing patterns, they are not good at explaining how they reach their decisions. Fuzzy logic systems,which can reason with imprecise information,are good at explaining their decisions but they cannot automatically acquire the rules they use to make those decisions. These limitations have been a central driving force behind the creation of intelligent hybrid systems where two or more techniques are combined in a manner that overcomes individual techniques
Fuzzy Neural Networks ◼ Introduction of fuzzy concepts into artificial neurons and neural networks ◼ For example, while neural networks are good at recognizing patterns, they are not good at explaining how they reach their decisions. ◼ Fuzzy logic systems, which can reason with imprecise information, are good at explaining their decisions but they cannot automatically acquire the rules they use to make those decisions. ◼ These limitations have been a central driving force behind the creation of intelligent hybrid systems where two or more techniques are combined in a manner that overcomes individual techniques
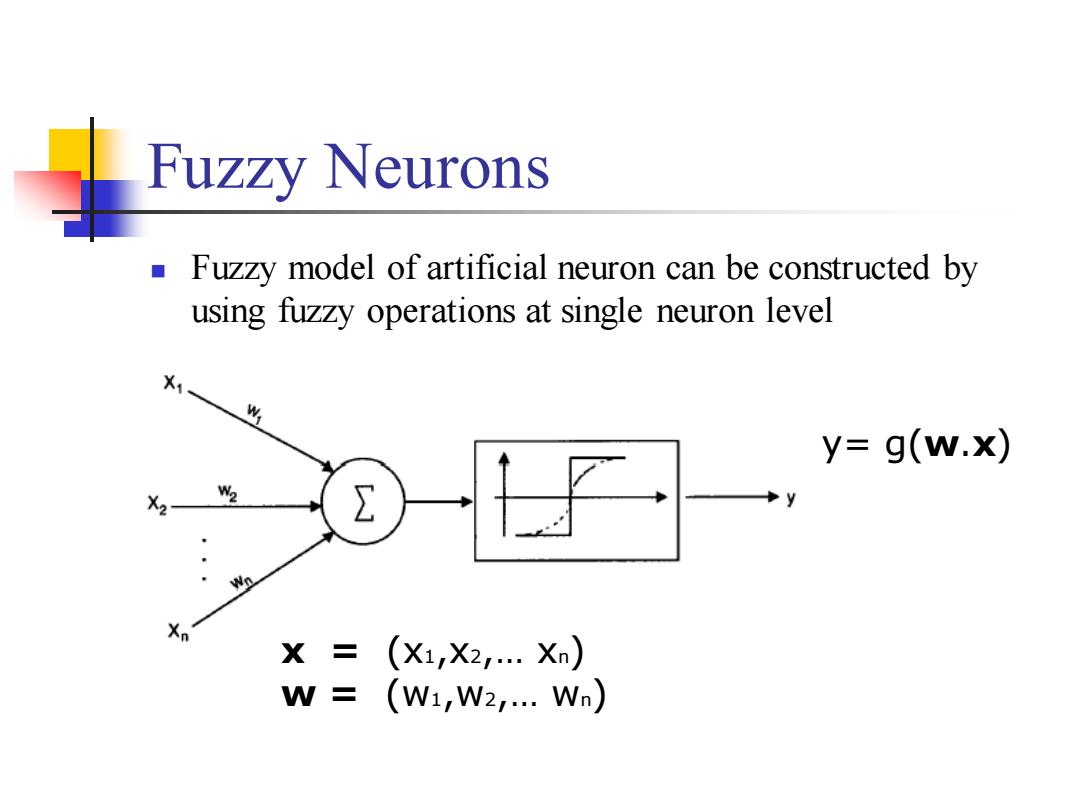
Fuzzy Neurons Fuzzy model of artificial neuron can be constructed by using fuzzy operations at single neuron level y=g(w.x) 2 % Xn X (X1,X2…Xn) W= (W1,W2,…Wn)
Fuzzy Neurons ◼ Fuzzy model of artificial neuron can be constructed by using fuzzy operations at single neuron level x = (x1,x2,… xn) w = (w1,w2,… wn) y= g(w.x)
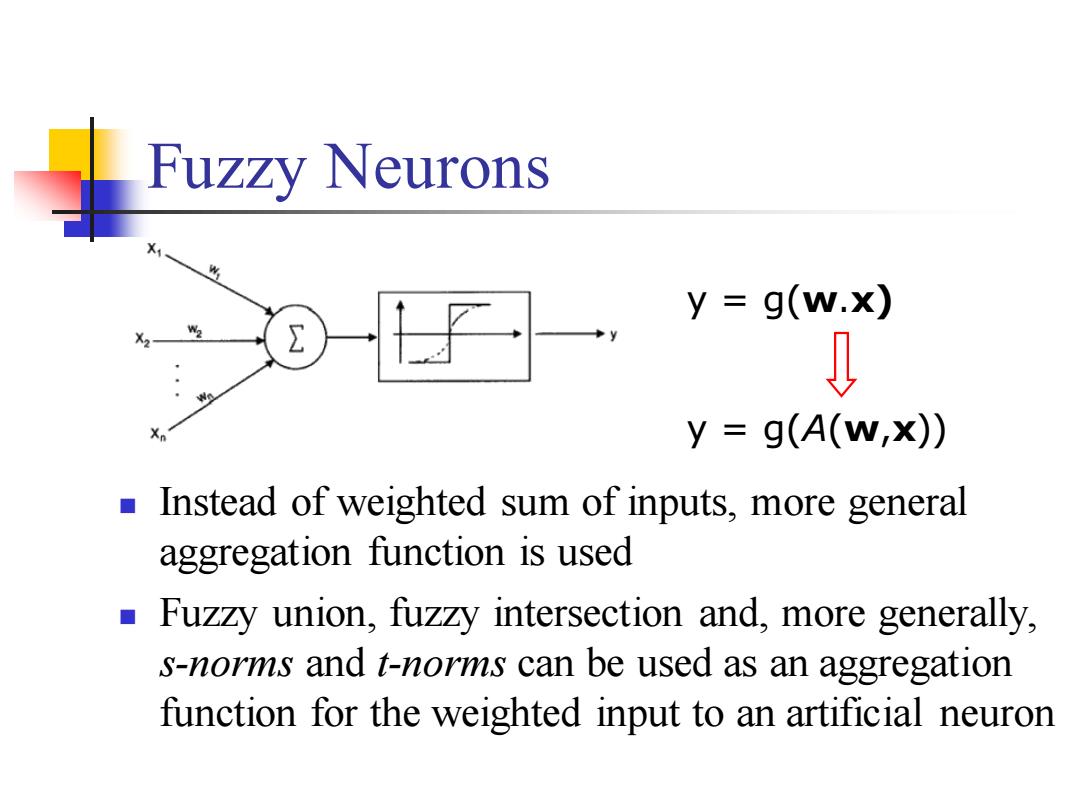
Fuzzy Neurons X y=g(w.x) y g(A(W,x)) Instead of weighted sum of inputs,more general aggregation function is used Fuzzy union,fuzzy intersection and,more generally. s-norms and t-norms can be used as an aggregation function for the weighted input to an artificial neuron
Fuzzy Neurons y = g(w.x) y = g(A(w,x)) ◼ Instead of weighted sum of inputs, more general aggregation function is used ◼ Fuzzy union, fuzzy intersection and, more generally, s-norms and t-norms can be used as an aggregation function for the weighted input to an artificial neuron
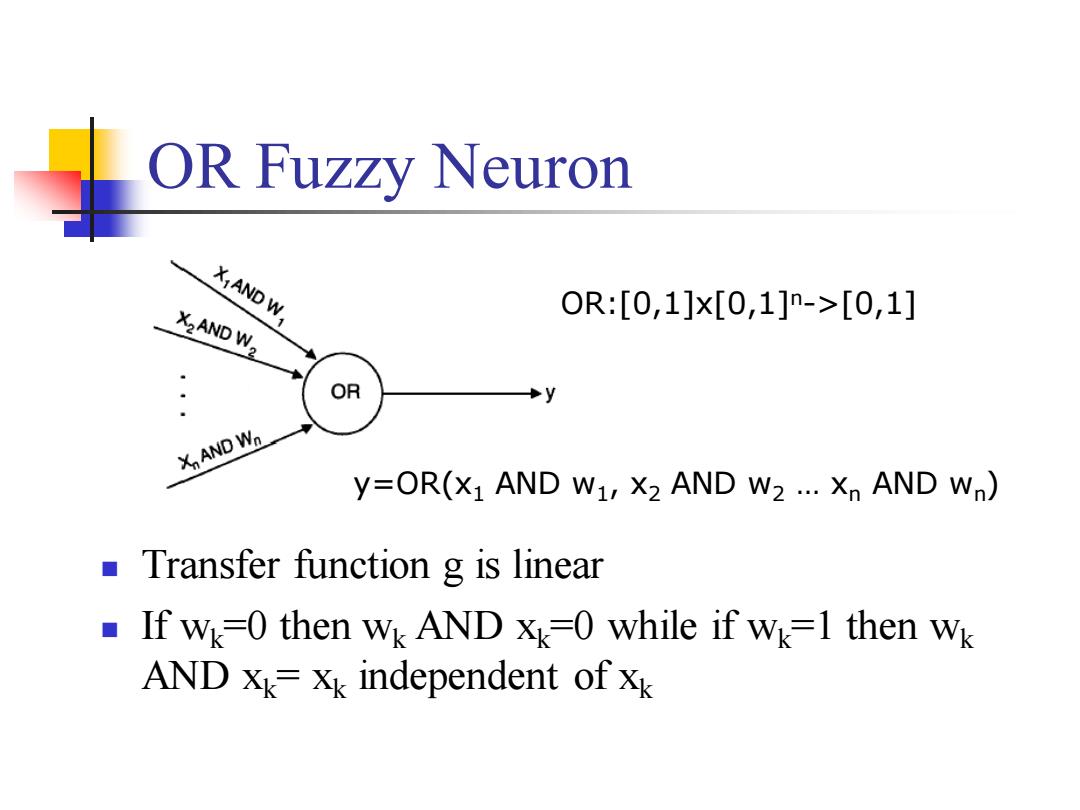
OR Fuzzy Neuron X AND W. X2AND W2 0R:[0,1]x[0,1]n->[0,1] OR y X AND Wn y=OR(X1 AND W1,X2 AND W2 ..Xn AND Wn) Transfer function g is linear If wk=0 then wk AND Xk-0 while if wk=1 then wk AND Xk=Xk independent of xk
OR Fuzzy Neuron ◼ Transfer function g is linear ◼ If wk=0 then wk AND xk=0 while if wk=1 then wk AND xk= xk independent of xk y=OR(x1 AND w1 , x2 AND w2 … xn AND wn) OR:[0,1]x[0,1]n->[0,1]

AND Fuzzy Neuron X OR W. AND:[0,1]x[0,1]n->[0,1] XOR W AND XnOR Wo y=AND(X1 OR W1,X2 OR W2 ..Xn OR Wn) In the generalized forms based on t-norms,operators other than min and max can be used such as algebraic and bounded products and sums
AND Fuzzy Neuron ◼ In the generalized forms based on t-norms, operators other than min and max can be used such as algebraic and bounded products and sums y=AND(x1 OR w1 , x2 OR w2 … xn OR wn) AND:[0,1]x[0,1]n->[0,1]

Fuzzy Neurons Both the OR and the aNd logic neurons are excitatory in character,i.e.Tx =Ty ■ Issue of inhibitory (negative)weights deserves a short digression ■ In the realm of fuzzy sets operations are defined in [0,1] Proper solution to make a weighted input inhibitory is to take fuzzy complement of the excitatory membership value-x= 1-x Input x=(x1,..x)is extended to X=(X1,…,XmX1,…,7Xn)
Fuzzy Neurons ◼ Both the OR and the AND logic neurons are excitatory in character, i.e. xk => y ◼ Issue of inhibitory (negative) weights deserves a short digression ◼ In the realm of fuzzy sets operations are defined in [0,1] ◼ Proper solution to make a weighted input inhibitory is to take fuzzy complement of the excitatory membership value x = 1-x ◼ Input x=(x1 ,..xn ) is extended to x=(x1 ,…,xn ,x1 ,…,xn )