
电工学↓ 第四章正弦交流电路 第一节正弦交流电的基本概念 第二节正弦交流电的相量表示法 第三节单一理想元件的交流电路 第四节LC串联的交流电路 第五节阻抗的串联与并联 第六节正弦交流电路的分析方法 第七节功率因数的提高 第八节正弦交流电路的谐振 第九节非正弦交流电路 习题 目录
第四章 正弦交流电路 第一节 正弦交流电的基本概念 第二节 正弦交流电的相量表示法 第三节 单一理想元件的交流电路 第四节 RLC串联的交流电路 第五节 阻抗的串联与并联 第六节 正弦交流电路的分析方法 第七节 功率因数的提高 第八节 正弦交流电路的谐振 第九节 非正弦交流电路 习 题 目录

电工学↓ 第一节正弦交流电的基本概念 正弦量 正弦量的三要素 返回
第一节 正弦交流电的基本概念 正弦量 正弦量的三要素 返回

正弦量: 电工学↓ 大小和方向随时间按正弦规律变化 的电压、电流和电动势统称为正弦量。 正弦信号的和、差、微积分等运算 结果仍是同频率的正弦信号。 当正弦信号作为电路的信号源时 电路中产生的响应仍是同频率的正弦 信号。 返回
一、正弦量: 大小和方向随时间按正弦规律变化 的电压、电流和电动势统称为正弦量。 正弦信号的和、差、微积分等运算 结果仍是同频率的正弦信号。 当正弦信号作为电路的信号源时, 电路中产生的响应仍是同频率的正弦 信号。 返回
正弦电流冫用三角函数表示为哈} i=Imsin(@t+w) 其波形如图 从表达式可以看出,当 ”、业确定后,正弦 量就被唯一地确定了, 所以这三个量统称为 正弦量的三要素。 返回
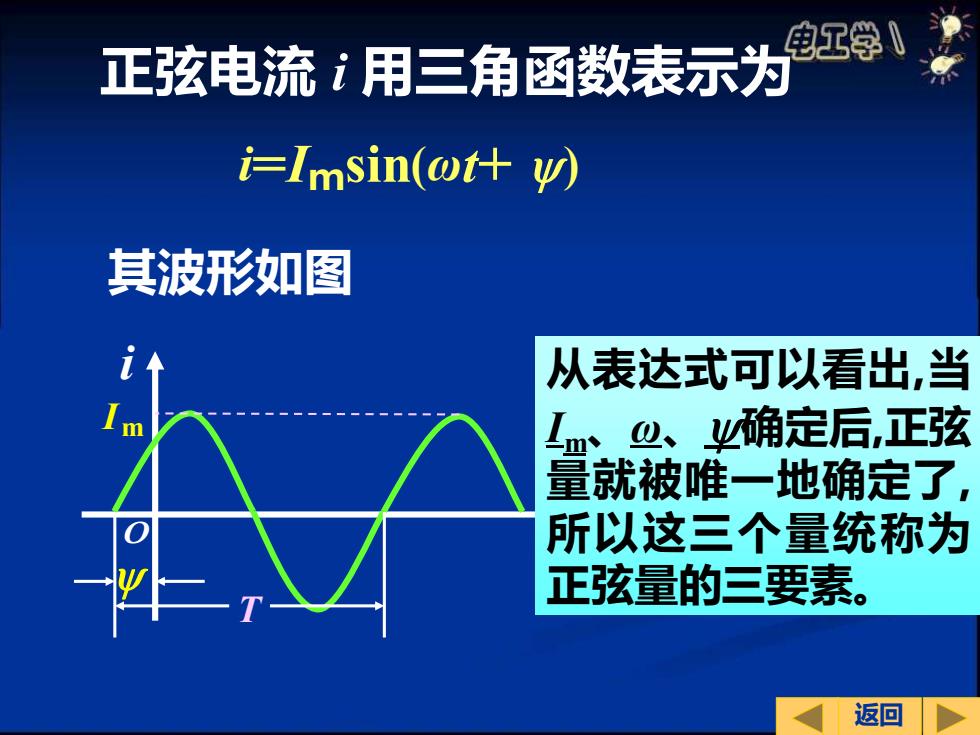
i=Imsin(ωt+ ) 其波形如图 t i Im T 从表达式可以看出,当 Im、ω、确定后,正弦 量就被唯一地确定了, 所以这三个量统称为 正弦量的三要素。 正弦电流 i 用三角函数表示为 返回 O

电工学↓ 二、正弦量的三要素 1.周期T、频率f和角频率w 2.最大值和有效值 3.相位、初相、相位差 返回
二、正弦量的三要素 1.周期T、频率f 和角频率ω 2.最大值和有效值 3. 相位、初相、相位差 返回

电工学↓ 1.周期T、频率f和角频率w 周期T:正弦量变化一次所需要的时 间称为周期。单位是秒(S)。 频率f:1s正弦量变化的次数称为频率 单位是赫兹Hz)。 显然f=1/T或T=1f 角频率0: 单位时间里正弦量变化的角度称为 角频率。单位是弧度秒(rad/s)。 0=2π/T=2元f 返回
周期T : 正弦量变化一次所需要的时 间称为周期。单位是秒 (s)。 频率f : 1s正弦量变化的次数称为频率。 单位是赫兹(Hz)。 显然 f =1/T 或 T =1/f 1.周期T、频率f 和角频率ω 角频率ω : 单位时间里正弦量变化的角度称为 角频率。单位是弧度/秒(rad/s)。 ω=2π/T=2πf 返回

电工学 周期,频率,角频率从不同角度描述 正弦量变化的快慢。三者只要知道其中之 便可以求出另外两个。 2.最大值和有效值 正弦量某一暖间的值称为瞬时值,瞬 时值中最大的称为最大值。Im、Um E分别表示电流、电压和电动势的 最大值。 表示交流电的大小常用有效值的概念。 返回
周期,频率,角频率从不同角度描述了 正弦量变化的快慢。三者只要知道其中之 一便可以求出另外两个。 2.最大值和有效值 正弦量某一瞬间的值称为瞬时值,瞬 时值中最大的称为最大值。Im、Um、 Em分别表示电流、电压和电动势的 最大值。 表示交流电的大小常用有效值的概念。 返回

把两个等值电阻分别通一交流电流爱、 和直流电流工。如果在相同的时间T内 所产生的热量相等,那么我们把这个直 流电流工定义为交流电流的有效值。 R=IRT即7=ra 所以交流电的有效值是瞬时值的方均根。 将电流的三角式带入上式中有: 1=1m/2 返回
把两个等值电阻分别通一交流电流i 和直流电流I。如果在相同的时间T内 所产生的热量相等,那么我们把这个直 流电流I定义为交流电流的有效值。 所以交流电的有效值是瞬时值的方均根。 2 2 0 d T i R t I RT = 即 2 0 1 d T I i t T = 将电流的三角式带入上式中有: I I = m 2 返回

同理: 电工学↓ U-U/V2 E-E m /V2 3.相位、初相、相位差 i=I sin(ot+YΨ)A 相位:我们把w什w称为相位。 初相:t=0时的相位称为初相y。 相位差:任意两个同频率的正弦 量的相位之差。用p表示。 返回
同理: m U U= 2 m E E = 2 3.相位、初相、相位差 m i I t = + sin( )A Ψ 相位:我们把 ωt+ 称为相位。 初相:t=0时的相位称为初相。 相位差:任意两个同频率的正弦 量的相位之差。用φ 表示。 返回

例1、u=Un sin(or+g,)着 i=I sin(ot+Ψ,)A 两者的相位差为:p=平,一平 电压超前电流Φ角 或电流滞后电压p角) 若:p 电压与电流同相位 电流超前电压p角 =土无电流与电压反相 返回
例1、 u U t = + m sin( )V u m sin( )Ai i I t = + Ψ 两者的相位差为: = − Ψu i Ψ >0 电压超前电流φ角 (或电流滞后电压φ 角) =0 电压与电流同相位 <0 电流超前电压φ角 = ±π 电流与电压反相 若:φ 返回