
第四节 管盘式折叠纸盒 一、管盘式折叠纸盒结构 对于凸多边形折叠纸盒,在其角隅处的任一 个旋转点上,必然满足TULIC-1公式 β = 360°-( α + Σ γ n) , 因为 β≤0 所以 ( α + Σ γ n) ≥360° 这意味着就传统异型盒的每一个旋转点来说, 以该点为顶点的所有成型角(包括A、B两类) 之和不能大于360°
第四节 管盘式折叠纸盒 一、管盘式折叠纸盒结构 对于凸多边形折叠纸盒,在其角隅处的任一 个旋转点上,必然满足TULIC-1公式 β = 360°-( α + Σ γ n) , 因为 β≤0 所以 ( α + Σ γ n) ≥360° 这意味着就传统异型盒的每一个旋转点来说, 以该点为顶点的所有成型角(包括A、B两类) 之和不能大于360°

而对于凹多边形折叠纸盒,由于在一个凹边 的旋转点上,A,B成型角之和大于360°。显然, 在一页纸板成型的条件下,单独采用管式或盘式 成型方法均不能使其成型。所以可以采用管盘式 成型方法,即用管式盒的旋转成型方法来成型盘 式盒的部分盒体,这就是管盘式折叠纸盒。 在图示ABCDEF凹六边形中,除∠AFE大于 180°外,其余五个角均小于180°。因此,从整体 上看,该盒型的六个体板中有五个可以盘式成型, 即体板与底板以一定角度(90°)折叠成型,相 邻体板在角隅处粘合
而对于凹多边形折叠纸盒,由于在一个凹边 的旋转点上,A,B成型角之和大于360°。显然, 在一页纸板成型的条件下,单独采用管式或盘式 成型方法均不能使其成型。所以可以采用管盘式 成型方法,即用管式盒的旋转成型方法来成型盘 式盒的部分盒体,这就是管盘式折叠纸盒。 在图示ABCDEF凹六边形中,除∠AFE大于 180°外,其余五个角均小于180°。因此,从整体 上看,该盒型的六个体板中有五个可以盘式成型, 即体板与底板以一定角度(90°)折叠成型,相 邻体板在角隅处粘合
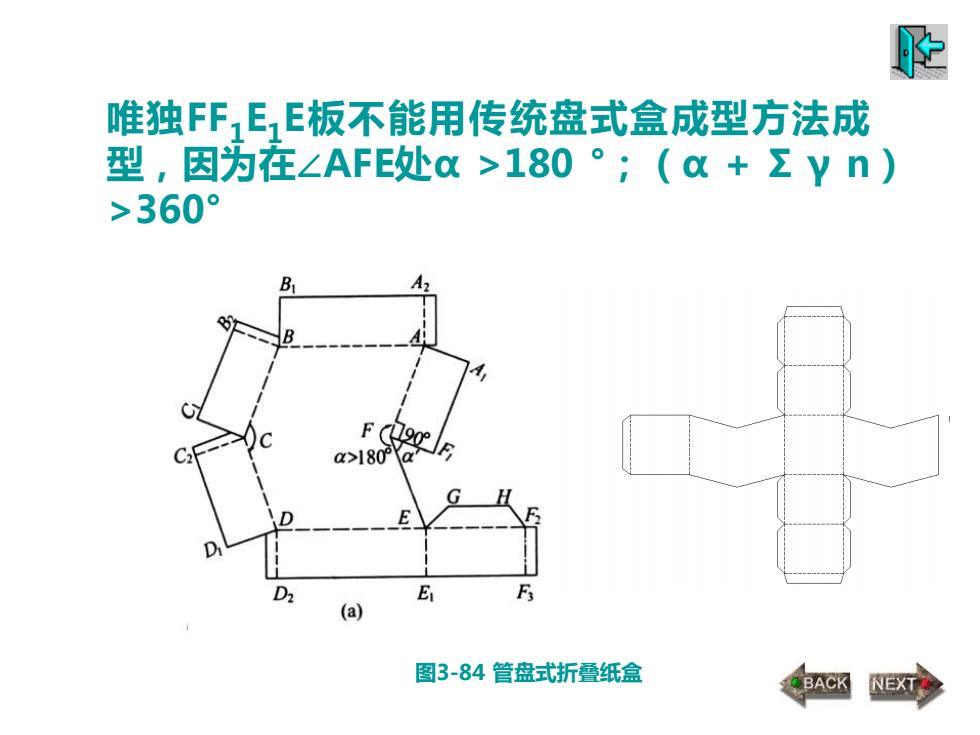
唯独FF1 E1 E板不能用传统盘式盒成型方法成 型,因为在∠AFE处α >180 °;(α + Σ γ n) >360° 图3-84 管盘式折叠纸盒
唯独FF1 E1 E板不能用传统盘式盒成型方法成 型,因为在∠AFE处α >180 °;(α + Σ γ n) >360° 图3-84 管盘式折叠纸盒
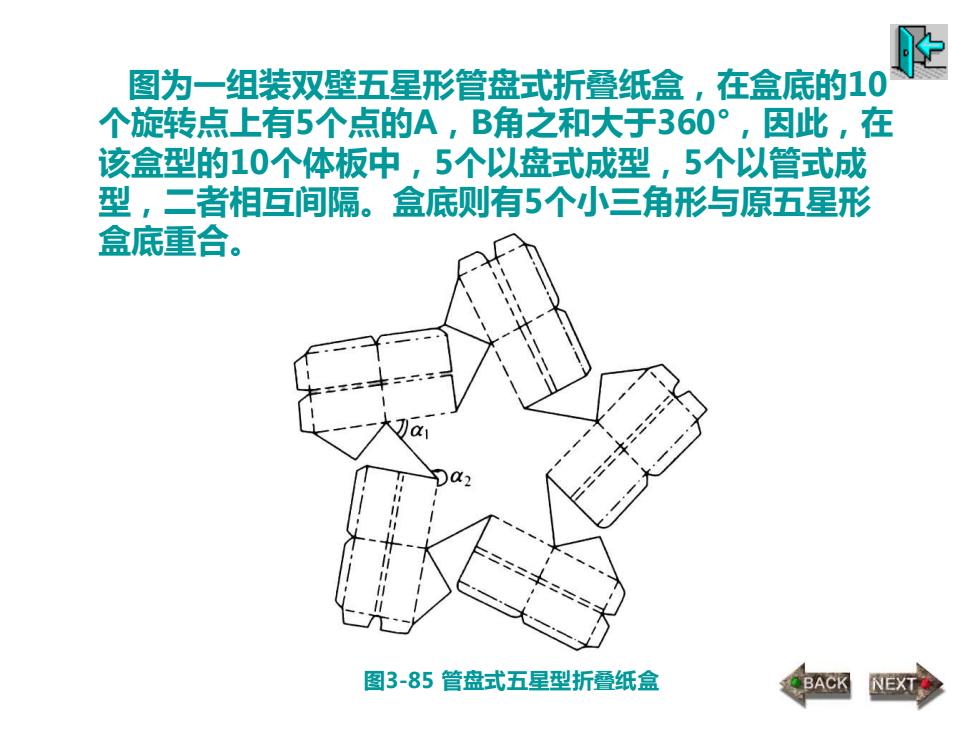
图为一组装双壁五星形管盘式折叠纸盒,在盒底的10 个旋转点上有5个点的A,B角之和大于360°,因此,在 该盒型的10个体板中,5个以盘式成型,5个以管式成 型,二者相互间隔。盒底则有5个小三角形与原五星形 盒底重合。 图3-85 管盘式五星型折叠纸盒
图为一组装双壁五星形管盘式折叠纸盒,在盒底的10 个旋转点上有5个点的A,B角之和大于360°,因此,在 该盒型的10个体板中,5个以盘式成型,5个以管式成 型,二者相互间隔。盒底则有5个小三角形与原五星形 盒底重合。 图3-85 管盘式五星型折叠纸盒
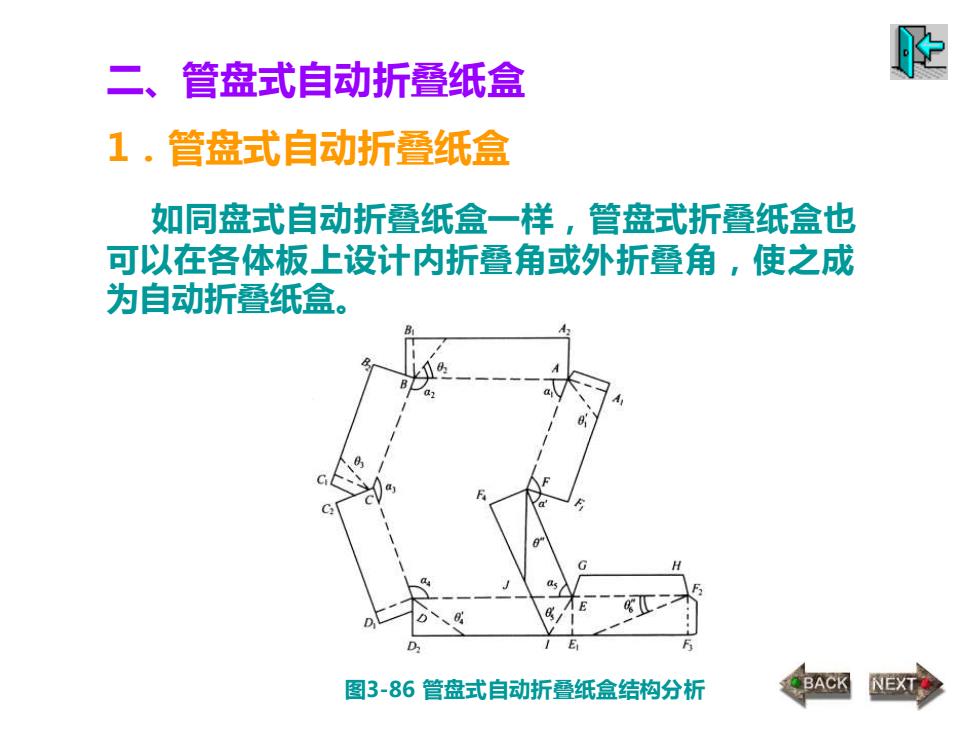
二、管盘式自动折叠纸盒 1.管盘式自动折叠纸盒 如同盘式自动折叠纸盒一样,管盘式折叠纸盒也 可以在各体板上设计内折叠角或外折叠角,使之成 为自动折叠纸盒。 图3-86 管盘式自动折叠纸盒结构分析
二、管盘式自动折叠纸盒 1.管盘式自动折叠纸盒 如同盘式自动折叠纸盒一样,管盘式折叠纸盒也 可以在各体板上设计内折叠角或外折叠角,使之成 为自动折叠纸盒。 图3-86 管盘式自动折叠纸盒结构分析

2.TULIC-5公式——管盘式折叠纸盒折叠 角(θ ")求解公式 设体板 FF1A1A 与 DD2 E1 E 均为外折叠, 其余为内折叠。这样,与 EE1 F3 F2 板相邻的 DD2 E1 E 板其中一条斜折线为EI, 外折叠角为θ 5' ,即∠IED。 ∠F1 FJ = ∠F4 FJ θ " =1/2(γ1 +γ2 -α' ) 图3-87 管盘式五星形自动折叠纸盒
2.TULIC-5公式——管盘式折叠纸盒折叠 角(θ ")求解公式 设体板 FF1A1A 与 DD2 E1 E 均为外折叠, 其余为内折叠。这样,与 EE1 F3 F2 板相邻的 DD2 E1 E 板其中一条斜折线为EI, 外折叠角为θ 5' ,即∠IED。 ∠F1 FJ = ∠F4 FJ θ " =1/2(γ1 +γ2 -α' ) 图3-87 管盘式五星形自动折叠纸盒