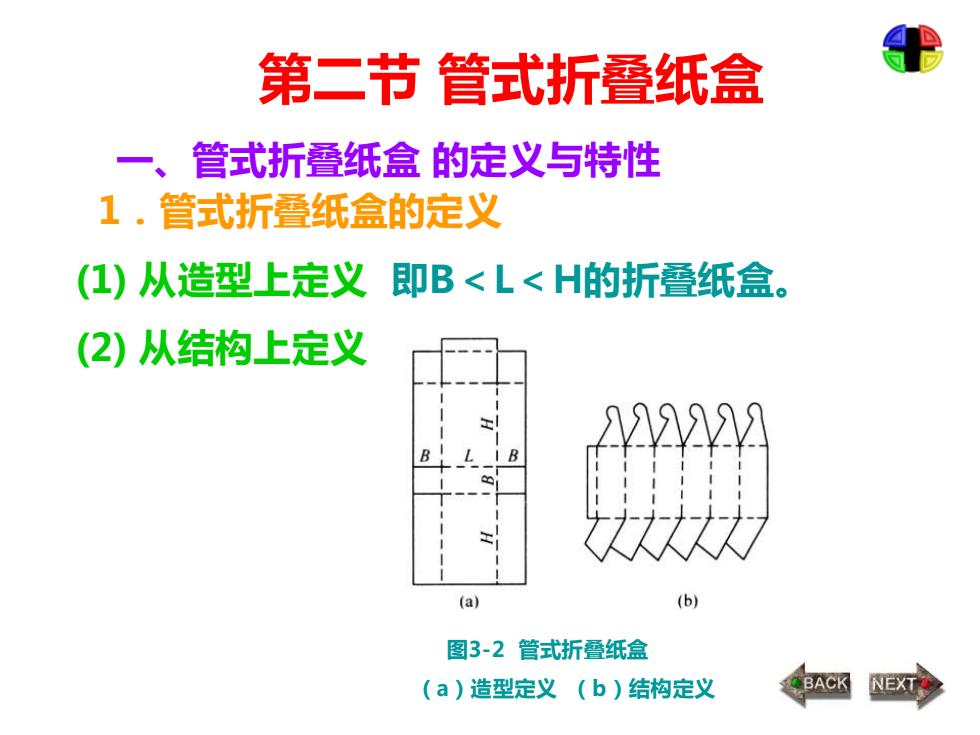
第二节 管式折叠纸盒 一、管式折叠纸盒 的定义与特性 1.管式折叠纸盒的定义 (1) 从造型上定义 即B<L<H的折叠纸盒。 (2) 从结构上定义 图3-2 管式折叠纸盒 (a)造型定义 (b)结构定义
第二节 管式折叠纸盒 一、管式折叠纸盒 的定义与特性 1.管式折叠纸盒的定义 (1) 从造型上定义 即B<L<H的折叠纸盒。 (2) 从结构上定义 图3-2 管式折叠纸盒 (a)造型定义 (b)结构定义
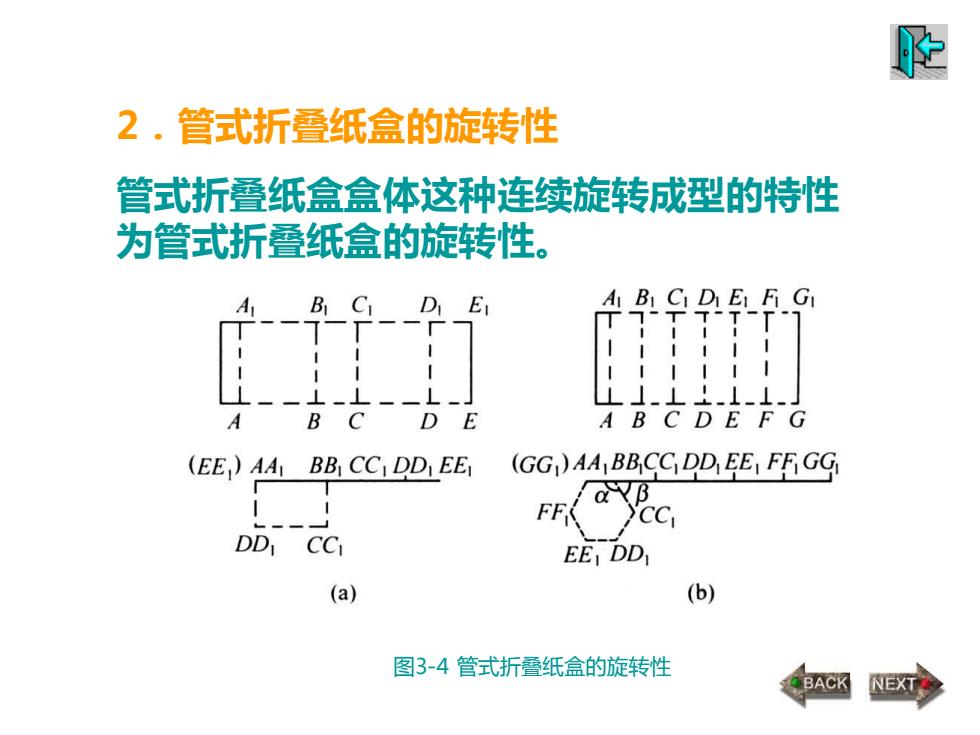
2.管式折叠纸盒的旋转性 管式折叠纸盒盒体这种连续旋转成型的特性 为管式折叠纸盒的旋转性。 图3-4 管式折叠纸盒的旋转性
2.管式折叠纸盒的旋转性 管式折叠纸盒盒体这种连续旋转成型的特性 为管式折叠纸盒的旋转性。 图3-4 管式折叠纸盒的旋转性
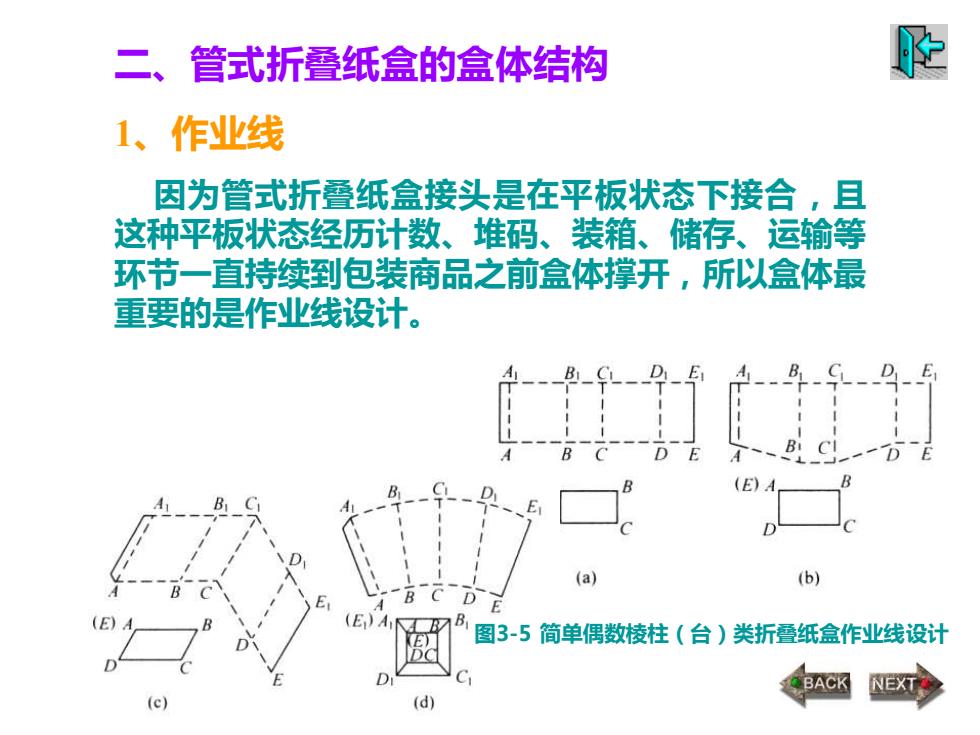
二、管式折叠纸盒的盒体结构 1、作业线 因为管式折叠纸盒接头是在平板状态下接合,且 这种平板状态经历计数、堆码、装箱、储存、运输等 环节一直持续到包装商品之前盒体撑开,所以盒体最 重要的是作业线设计。 图3-5 简单偶数棱柱(台)类折叠纸盒作业线设计
二、管式折叠纸盒的盒体结构 1、作业线 因为管式折叠纸盒接头是在平板状态下接合,且 这种平板状态经历计数、堆码、装箱、储存、运输等 环节一直持续到包装商品之前盒体撑开,所以盒体最 重要的是作业线设计。 图3-5 简单偶数棱柱(台)类折叠纸盒作业线设计
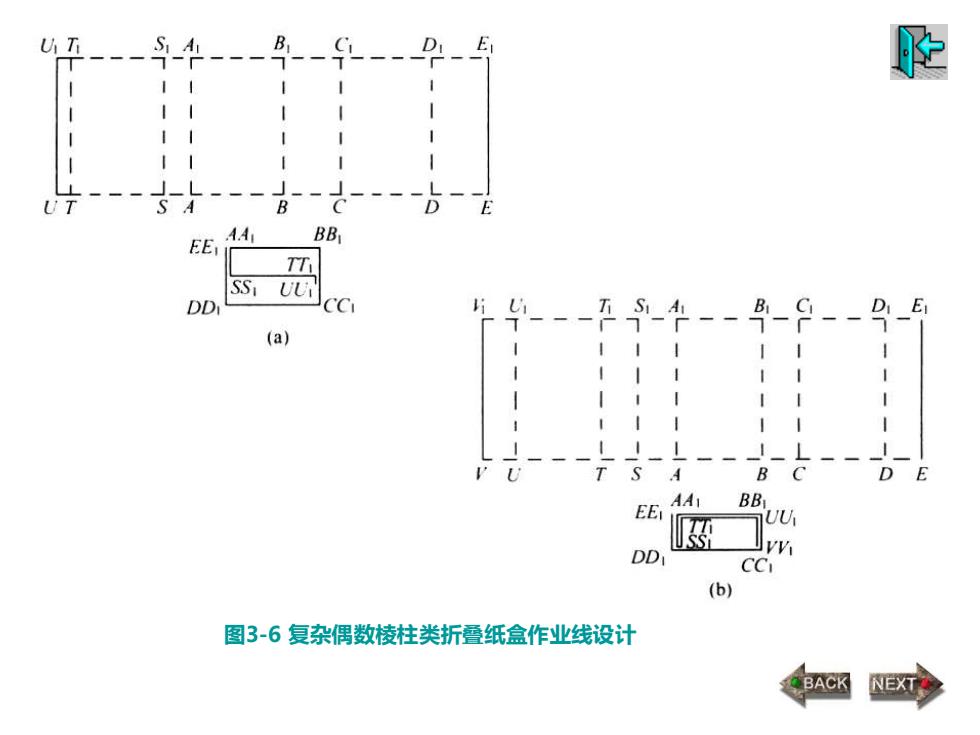
图3-6 复杂偶数棱柱类折叠纸盒作业线设计
图3-6 复杂偶数棱柱类折叠纸盒作业线设计
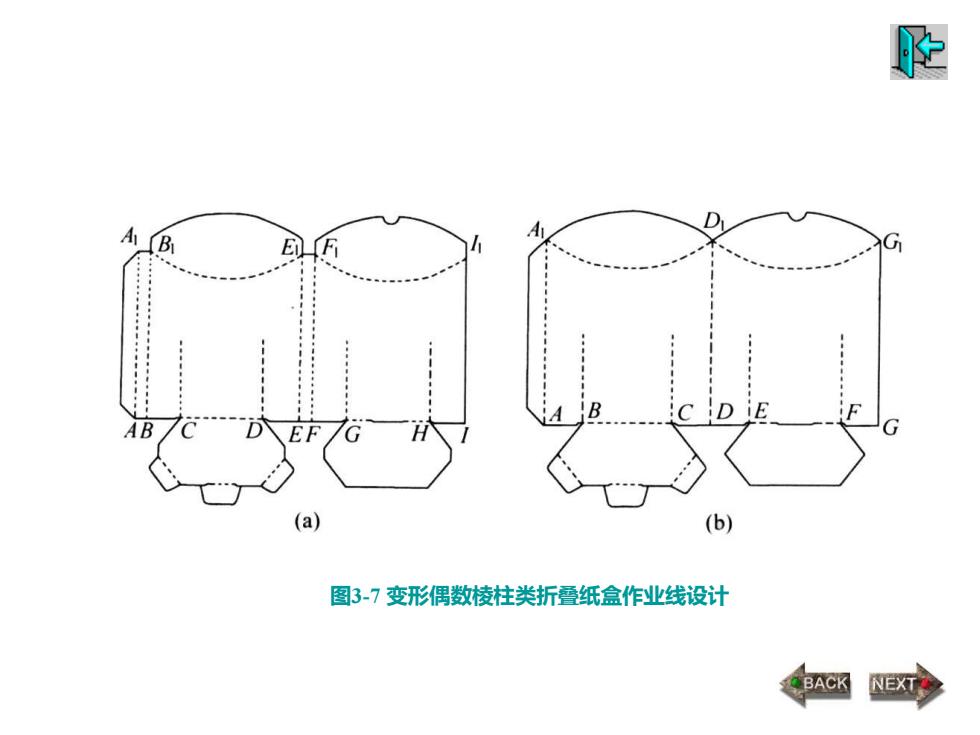
图3-7 变形偶数棱柱类折叠纸盒作业线设计
图3-7 变形偶数棱柱类折叠纸盒作业线设计

2、印刷面半切线 对于图3-8所示奇数棱柱类盒型,同样也要考虑到 平板状接合接头、平板状运输堆码等问题,所以也要设 计两条工作线CC1与AA1,其中CC1在折叠立体时起成 型作用,而AA1不起成型作用,它是一条单纯的作业压 痕线。 对于部分异形折叠纸盒,其成型折叠线不能使盒坯 两端在平折后对齐重合,这时必须重新设计两条垂直方 向的作业线,而且作业线应视情况延长穿越盖板(襟片) 或底板(襟片),如图3-9(a)的BF1线和DG1线,图3- 9(b)的FF1线和GG1线。这两条也是单纯的作业线。 为了不影响纸盒印刷面外观,单纯的作业线可以采用印 刷面半切线,即切线切缝深度均为纸板厚度的1/2(图 3-10),这样当成型立体盒型时,不会显露折痕
2、印刷面半切线 对于图3-8所示奇数棱柱类盒型,同样也要考虑到 平板状接合接头、平板状运输堆码等问题,所以也要设 计两条工作线CC1与AA1,其中CC1在折叠立体时起成 型作用,而AA1不起成型作用,它是一条单纯的作业压 痕线。 对于部分异形折叠纸盒,其成型折叠线不能使盒坯 两端在平折后对齐重合,这时必须重新设计两条垂直方 向的作业线,而且作业线应视情况延长穿越盖板(襟片) 或底板(襟片),如图3-9(a)的BF1线和DG1线,图3- 9(b)的FF1线和GG1线。这两条也是单纯的作业线。 为了不影响纸盒印刷面外观,单纯的作业线可以采用印 刷面半切线,即切线切缝深度均为纸板厚度的1/2(图 3-10),这样当成型立体盒型时,不会显露折痕
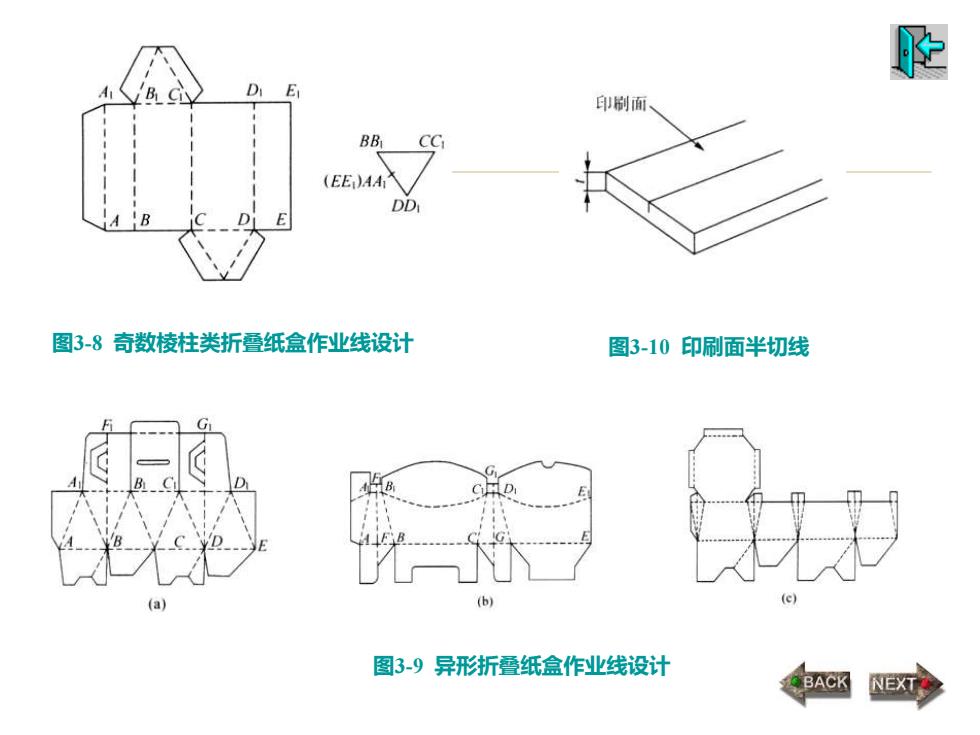
图3-8 奇数棱柱类折叠纸盒作业线设计 图3-9 异形折叠纸盒作业线设计 图3-10 印刷面半切线
图3-8 奇数棱柱类折叠纸盒作业线设计 图3-9 异形折叠纸盒作业线设计 图3-10 印刷面半切线

3、直四棱台作业线的研究 直四棱台折叠纸盒设计作业线必须满足的条件 图3-11 直四棱台折叠纸盒盒体展开图 根据作业线设计的条件,当 平折时 aa′和ee′的位置必 须重合,则应满足Xa1=Xe1, Ya1=Ye1;Xa2=Xe2,Ya2=Ye2, 从而可导出: L/B=cosγ1 / cosγ2 式中, L——直四棱台折叠纸盒下底的长,mm B——直四棱台折叠纸盒下底的宽,mm γ1——直四棱台折叠纸盒侧板底角(B成型角),(°) γ2——直四棱台折叠纸盒端板底角(B成型角),(°) 该式即为直四棱台折叠纸盒设计作业线必须满足的条件
3、直四棱台作业线的研究 直四棱台折叠纸盒设计作业线必须满足的条件 图3-11 直四棱台折叠纸盒盒体展开图 根据作业线设计的条件,当 平折时 aa′和ee′的位置必 须重合,则应满足Xa1=Xe1, Ya1=Ye1;Xa2=Xe2,Ya2=Ye2, 从而可导出: L/B=cosγ1 / cosγ2 式中, L——直四棱台折叠纸盒下底的长,mm B——直四棱台折叠纸盒下底的宽,mm γ1——直四棱台折叠纸盒侧板底角(B成型角),(°) γ2——直四棱台折叠纸盒端板底角(B成型角),(°) 该式即为直四棱台折叠纸盒设计作业线必须满足的条件
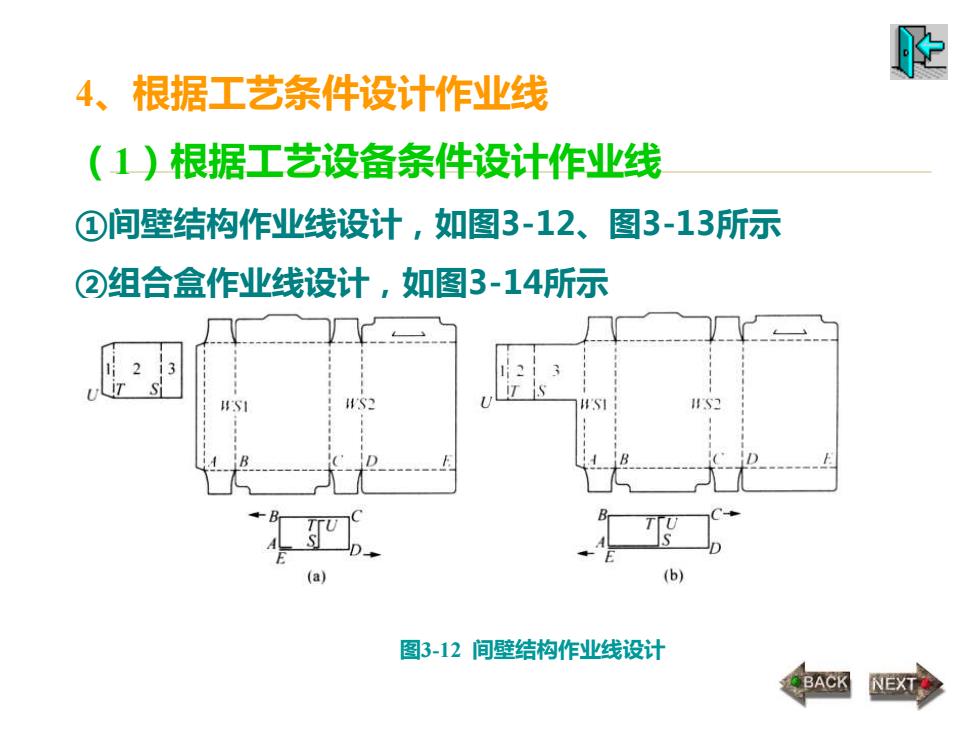
4、根据工艺条件设计作业线 (1)根据工艺设备条件设计作业线 ①间壁结构作业线设计,如图3-12、图3-13所示 ②组合盒作业线设计,如图3-14所示 图3-12 间壁结构作业线设计
4、根据工艺条件设计作业线 (1)根据工艺设备条件设计作业线 ①间壁结构作业线设计,如图3-12、图3-13所示 ②组合盒作业线设计,如图3-14所示 图3-12 间壁结构作业线设计
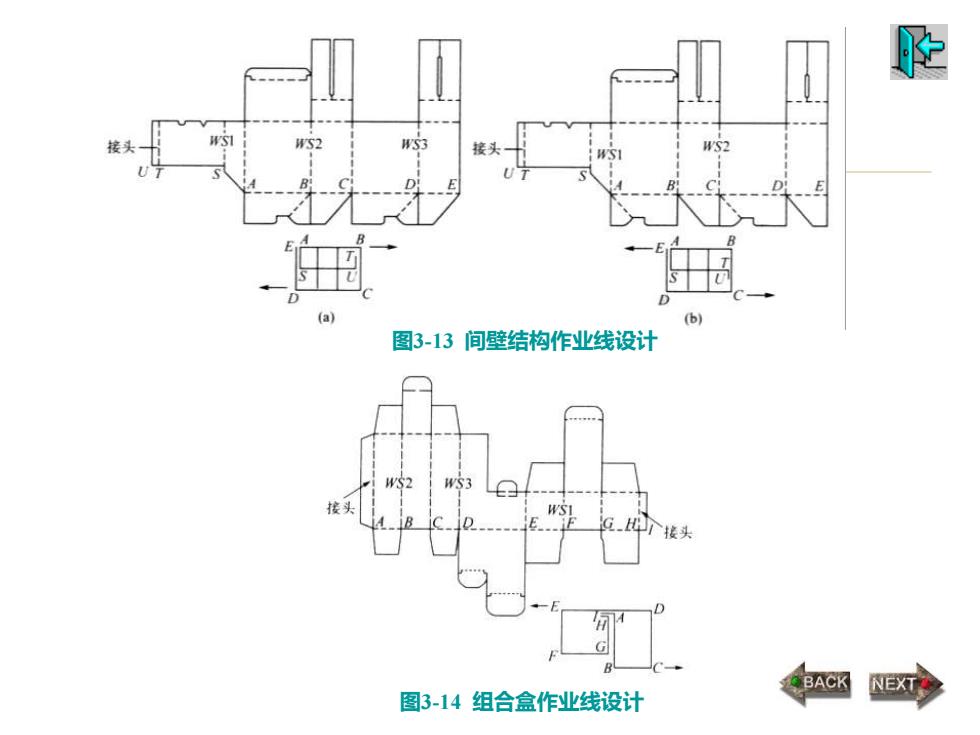
图3-13 间壁结构作业线设计 图3-14 组合盒作业线设计
图3-13 间壁结构作业线设计 图3-14 组合盒作业线设计