
Chapter 3 The z-Transform ◆3.0 Introduction ◆3.1z-Transform 3.2 Properties of the Region of Convergence for the z-transform 3.3 The inverse z-Transform 3.4 z-Transform Properties 3.5 z-Transform and LTI Systems 3.6 the Unilateral z-Transform 2
2 Chapter 3 The z-Transform ◆3.0 Introduction ◆3.1 z-Transform ◆3.2 Properties of the Region of Convergence for the z-transform ◆3.3 The inverse z-Transform ◆3.4 z-Transform Properties ◆3.5 z-Transform and LTI Systems ◆3.6 the Unilateral z-Transform

3.0 Introduction Fourier transform plays a key role in analyzing and representing discrete-time signals and systems,but does not converge for all signals. -品=24 1-ae jo 1-ae -ae Continuous systems:Laplace transform is a generalization of the Fourier transform. Discrete systems z-transform,which is a generalization of DTFT,converges for a broader class of signals 3
3 3.0 Introduction ◆Fourier transform plays a key role in analyzing and representing discrete-time signals and systems, but does not converge for all signals. ◆Continuous systems: Laplace transform is a generalization of the Fourier transform. ◆Discrete systems : z-transform, which is a generalization of DTFT, converges for a broader class of signals. xn a un n = a 1 DTFT 0 1 1 j ae − = − n n jwn a u n e =− − ! 1 ( ) 1 j j ae ae − − − = −

3.1 z-Transform X(e)=∑x[neom→∑n]z" n=-o0 Z=reia ◆If elo>z,Fourier transform→z-transform z-Transform:two-sided,bilateral z-transform X(z)=∑x[nzn=z{x[n]} n=-00 m←2→X(z) ◆one-sided, unilateral z-transform UX(z)=z)=∑x[nz n=0 Go 5
5 3.1 z-Transform ( ) j n j n X e x n e =− − = ( ) [ ] n n X z x n x n z =− − = = Z 0 n n x n z − = = ◆one-sided, unilateral z-transform ◆z-Transform: two-sided, bilateral z-transform x n X z [ ]⎯→ ( ) Z ◆If , j e z → Fourier transform z-transform n n x n z =− → − j Z = reGo UX z( ) =

Relationship between z-transform and Fourier transform Express the z in polar form as X(z)=∑x[n]z” =X(rem)=∑(x[nlr")emm n=-o0 z-transform is the Fourier transform of the product of xn and( (the exponential sequence ) Ifr=Z-l,X(Z)→X(eo) 6
6 ◆Express the z in polar form as Relationship between z-transform and Fourier transform j Z = re ( ) ( ) j n j n n X e re x n r − = − − = = ◆z-transform is the Fourier transform of the product of and (the exponential sequence ). x n n r − If X Z r Z = = 1, ( ) ( ) n n X z x n z =− − = ( ) j X e
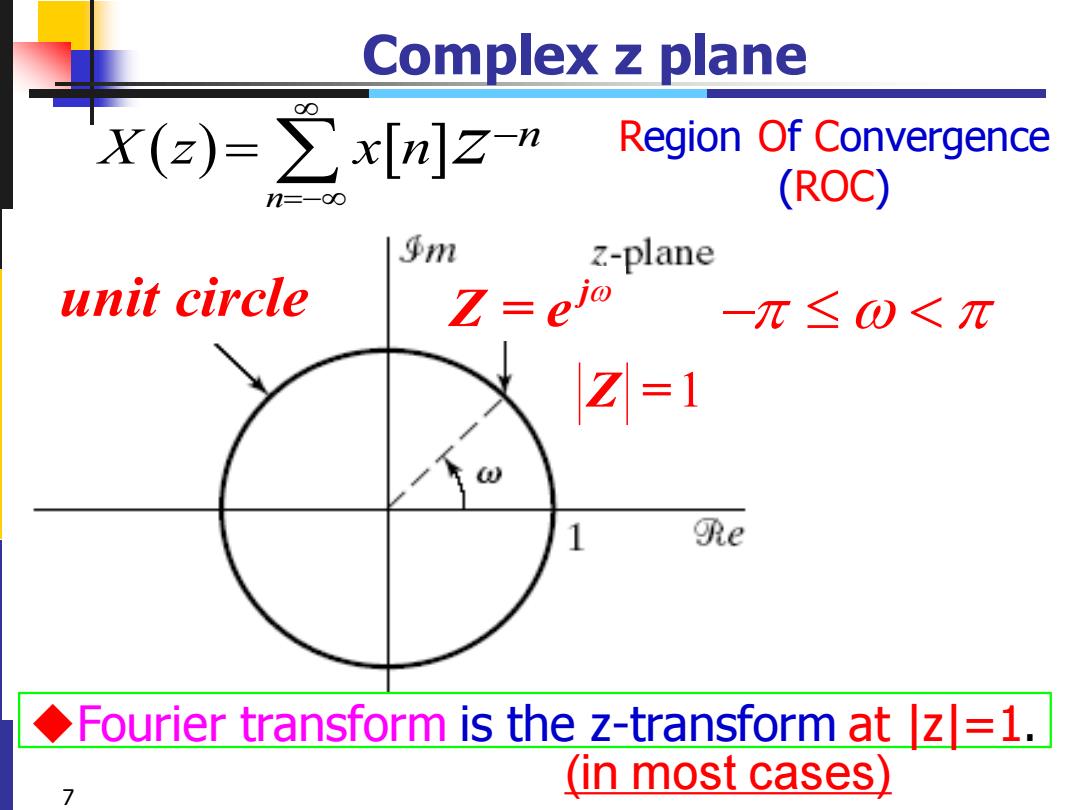
Complex z plane X(z)=∑x[n]z-n Region Of Convergence n=-00 (ROC) 乎m Z-plane unit circle Z=eio -π≤①<π Z=1 1 e Fourier transform is the z-transform at z|=1. (in most cases) 7
7 Complex z plane ( ) n n X z x n z =− − = j unit circle Z = e − Z =1 Region Of Convergence (ROC) ◆Fourier transform is the z-transform at |z|=1. (in most cases)

Region of convergence (ROC) For any given sequence,the set of values of z for which the z-transform converges is called the Region Of Convergence(ROC). X(z)=∑x[nz"→x(z≤∑[n]lz”. n=-00 z=re n=-00 Absolute Summability X(eo)=∑([n-")eom 1n二-00 X(re∑[n]r<∞ n=-00 Convergence of the z-transform for a given sequence depends only on r=z 8
8 Region of convergence (ROC) ◆For any given sequence, the set of values of z for which the z-transform converges is called the Region Of Convergence (ROC). ( ) n n X z x n z − =− = [ ] j n n X re x n r − =− ( ) ( ) [ ] n n X z x n z − = - j z re = Absolute Summability ( [ ] ) j n j n n X re x n r e − − =− ( )= r z = ◆Convergence of the z-transform for a given sequence depends only on

Region of convergence (ROC) X(z≤∑x[n]lz"<o, z=rew n=-00 Convergence of the z-transform for a given sequence depends only on r=z z-plane if some value of z,say, unit circle Z =Z1,is in the ROC, then all values of z on the circle defined by =zil 欧e will also be in the ROC. 傅里叶变换一致收敛uniform convergence 设z=|z1=1 在收敛域内 if ROC includes unit circle,then Fourier transform and all its derivatives with respect to must be continuous functions of
z1 if some value of z, say, z =z1 , is in the ROC, then all values of z on the circle defined by |z|=|z1 | will also be in the ROC. if ROC includes unit circle, then Fourier transform and all its derivatives with respect to must be continuous functions of . ( ) , - n n X z x n z − = ◆Convergence of the z-transform for a given sequence depends only on r z = . Region of convergence (ROC) j z re = 傅里叶变换一致收敛uniform convergence 9 设|z|=|z1 |=1 在收敛域内 unit circle
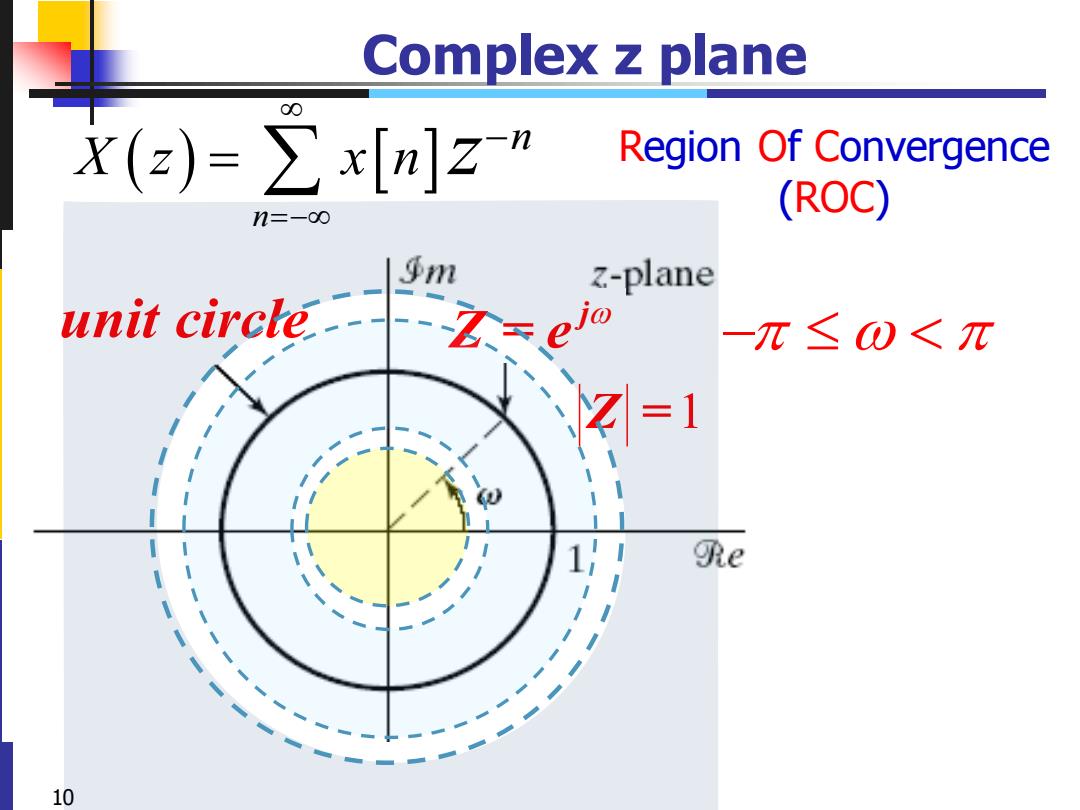
Complex z plane 00 X(z)=∑x[n]zn Region Of Convergence n=-o0 (ROC) 乎m Z-plane unit circle --Z< ejo -π≤0<π =1 1 e 10
10 Complex z plane ( ) =− − = n n X z x n z j unit circle Z = e − Z =1 Region Of Convergence (ROC)

Region of convergence (ROC) drk,[]-i,a小-co@wnhoneither of them is absolutely summable,and neither multiplied by r"(-ooHIp[n]is square-summable,so it's Fourier transform converges in mean-square sense to a discontinuous periodic function. x[n]is neither absolutely nor square summable,but a useful Fourier transform for x[n]can be defined using impulse functions-> 11
11 Region of convergence (ROC) ( 0 ) sin , [ ] cos , lp c n for h n x n n n = = ➢neither of them is absolutely summable, and neither multiplied by r -n (-∞<n<∞) would be absolutely summable for any value of r . Thus, neither has a z-transform that converges absolutely for any z . ➢Hlp[n] is square-summable, so it’s Fourier transform converges in mean-square sense to a discontinuous periodic function. -∞<n<∞ x[n] is neither absolutely nor square summable, but a useful Fourier transform for x[n] can be defined using impulse functions→

Region of convergence (ROC) sino.n πn →以etag -00<n<0 cos(aw)→∑[π(o-@a+2r)+π6(@+a+2πk] FTs aren't uniform convergence傅里叶变换不是一致收敛 The Fourier transforms aren't continuous,infinitely differentiable functions,so they cannot result from evaluating a z-transform on the unit circle. So it's not strictly correct to think of the Fourier transform as being the z-transform evaluated on the unit circle. 12
12 Region of convergence (ROC) ➢The Fourier transforms aren’t continuous, infinitely differentiable functions, so they cannot result from evaluating a z-transform on the unit circle. cos(0 n) ( 0 0 2 2 ) ( ) k k k =− − + + + + So it’s not strictly correct to think of the Fourier transform as being the z-transform evaluated on the unit circle. FTs aren’t uniform convergence傅里叶变换不是一致收敛 − n sin lp c n h n n = ( ) 1, 0, j c lp c H e =