
第7卷第4期 智能系统学报 Vol.7 No.4 2012年8月 CAAI Transactions on Intelligent Systems Aug.2012 D0I:10.3969/j.issn.16734785.201111007 网络出版地址:htp://www.cnki.net/kcms/detail/23.1538.TP.20120712.1022.003.html 离散时间混合多智能体的拟平均一致性控制 李波,吴淑琴1,谷明琴2 (1.郑州威科姆科技股份有限公司卫星定位应用工程技术研究中心,河南郑州450000:2.中南大学信息工程学 院,湖南长沙410083) 摘要:为了研究混合一阶和二阶异质无向多智能体网络离散时间一致性问题,提出了固定和可变拓扑结构的多智 能体网络的拟平均一致性协议.根据Lyapunov函数和代数图论,分析了多智能体网络的稳定性,表明在固定和可变 拓扑结构的情况下,混合阶多智能体系统可以达到拟平均一致.对6个节点组成的4种不同的无向网络拓扑结构进 行了仿真,结果显示了变拓扑离散时间异质多智能体网络的位置和速度均能达到拟平均一致.仿真结果表明,该算 法对混合阶多智能体网络的拟平均一致性控制有数. 关键词:一致性问题:异质多智能体:拟平均一致性:离散时间 中图分类号:TP18文献标志码:A文章编号:16734785(2012)04-035206 Quasi-average-consensus control of hybrid swarm agents with discrete time LI Bo',WU Shuqin',GU Mingqin2 (1.Satellite Positioning Application Engineering Research Center,Zhengzhou VCOM Science and Technology Co.,Ltd.,Zhengzhou 450000,China:2.School of Information Science and Engineering,Central South University,Changsha 410083,China) Abstract:The consensus problem of time discrete for undirected multi-agent networks with heterogeneous nodes of mixed first and second order integrators was covered in this paper.Corresponding quasi-average-consensus protocol was proposed for both fixed and switching topology cases.The stability of a multi-agent network was analyzed ac- cording to the Lyapunov function and algebra graph theory,and it was suggested that the mixed order multi-agent system can reach a quasi-average-consensus in a fixed and variable topology structure.Four different topologies of the network structure with 6 nodes were simulated,and the results show that the position and velocity of the discrete time variable topology of a heterogeneous multi-agent network can reach a quasi-average-consensus.The simulation results show that the algorithm is effective for quasi-average-consensus control of mixed order multi-agent networks. Keywords:consensus problem;heterogeneous multi-agent;quasi-average consensus;discrete time 近年来,多智能体的分布式协调控制如编队控合阶多智能体离散动力学网络的拟平均一致性问 制12]、群集问题3]、分布式传感器网络4、通信网题,并提出一致性协议解决该问题.用Lyapunov函 络的拥塞控制]等领域受到了极大的关注.Vicsek 数和代数图论分析系统的稳定性,实验结果表明,该 等提出了一个简单的自驱动的粒子群相变和数值型 方法能够有效解决混合阶多智能体离散动力学网络 复杂动力学的模型6,Jadbabaie等用图论对Vicsek 的拟平均一致性问题, 模型在理论上进行了解释];Olfati-Saber21和Mur ray1介绍了网络动力学一致性问题的理论框架;文 1 图论和一致性协议 献[9]提出了分析多智能体系统的理论框架;Lin等 1.1图论 分析了具有变拓扑和耦合时间延迟的多智能体网络 令G=(V,e,A)为加权无向图,其n阶顶点集 平均一致性问题),及二阶多智能体网络的一致性 V={u1,2,…,n},边集e=V×V,加权邻接矩阵 控制问题.与上述方法不同,本文研究了具有混 A=(a),ag≥0.节点的下标属于有限下标集I= 收稿日期:2011-11-14.网络出版日期:201207-12. {1,2,…,n,G的边集记为eg=(,西).与边相关联 通信作者:李波.E-mail:lho@zzvcom.com 的n×n阶接矩阵A的元素均为非负,如式(1)所示

第4期 李波,等:离散时间混合多智能体的拟平均一致性控制 ·353· rag=0,eg年e, 专:(k+1)=A5:(k)+Bu:(k). (3) as =0,VieI, (1) 式中::(k)=[x:(k):(k)]T是二阶智能体的状 Lag>0,e∈e. 态,4:()是控制输入.矩阵A、B分别为: 因而,如果图G=(V,E,A)是无向图或平衡图, 那么A就是对称矩阵。 4=0a=[7 集合N={)∈:(:,)∈}表示为:的邻集, 每个一阶智能体的动力学方程可以表示为差分 节点集V的任一子集J称为簇簇J的邻集定义为 方程形式: N=U,N={y∈V::∈J,(,y)∈e 5:(k+1)=专(k)+u:(k) 式中:专:(k)=x:(k) 节点:的入度、出度定义为 定义2离散时间的拟平均一致性问题:假设 dego)月.deg.()-r G=(V,e,A)是强连通有向网络或连通无向网络. 如果存在一个渐近的稳定平衡点专·,满足: 对于邻接元素为0-1的图,deg(u:)-1Nl.图G的 r[e0]T,i∈{1,2,…,n2; 度矩阵等于对角阵A=[△]. 5= 专,ie{1,2,…,n1k (4) 式中: ∫4g=0,i≠j, ijel. lAa=degou(v:), 式中:话=(0)+月(0)+0)》, 2 图G的Laplacian矩阵定义为 a∈R,那么就称式(4)为拟平均一致性问题 L(G)=4-A. 提出下面的一致性协议解决混合阶异质积分智 由定义知,如果图G是平衡图或无向图,那么Lapla- 能体网络中的一致性问题. cian矩阵的每行元素之和为零.因此,Laplacian矩阵 1.3一致性协议 有一个特征值为零,与零特征值所对应的右特征向 定义3对于定拓扑和变拓扑网络,可以用一 量为 致性协议来解决拟平均一致性问题: 4(k+1)= w,=1/.=1/Vn11…1]fxa 用G(t)表示变拓扑无向或有向网络,其中切换信 「-因+g∑,马)-(因)1e12,h, 号为sw(t):[0,+o)→{1,2,…,M},M∈Z+.L lg∑凸-年()e12,…n 表示变拓扑网络的Laplacian矩阵. 引理1[)令G=(V,6,A)为加权无向图或有 (5) 式中:a:是图的邻接矩阵的元素,步长:>0. 向图,其Laplacian矩阵为L.无向图G节点的最大 那么式(2)、(3)可以写为统一的形式: 出度,记为dnma(G)=max,degt(:).那么,L(G)的 (k+1)=P(k). 所有特征值都位于所定义的圆盘内部: 式中:P=M+I-gL,M=diag(M1,M2,…,Mn)= D(G)=ER:I 2-dn(G)Is dmnn(G). r0,i=1,2,…,n1 1.2一致性问题 定义1令X:R"→R是n变量的函数5i,专2, 8il=+1,2, I是(n+n2)×(n+ …,专.,(0)记为系统的初始状态.动力学网络中的 2)的单位阵,对于一阶智能体,L在分块意义下,保 X一致性问题是输人山:计算x((0)的分布式方 持不变.而对于二阶智能体,在位置上保持不变,但 式,且仅依赖于节点:自己和它邻近的状态.称状 在速度上增加零行和零列. 态反馈 图1是具有4个异质积分智能体的无向网络拓 4=k(与52,…5) (2) 扑结构(其中节点13是二阶智能体,而节点2、4是 是图G的协议,如果索引集为ji2,…jn∈1的节点 一阶智能体).那么对应于图1的矩阵M、立、L、P可 簇J={2,,}满足特性J,G{:}UN当且 以写为: 仅当存在一个渐近稳定平衡点专·满足专·= Γ0000 0 0 X((0)),就称协议渐近解决了一致性问题 000 0 0 0 假设多智能体系统是混合一、二阶的异质多智 M= 000 1 0 0 能体系统.智能体的总个数为n,其中一阶和二阶智 00 -1 0 0 能体个数分别为n1、2,每个二阶智能体的动力学方 000 0 1 程可以表示为差分方程形式: L000 0 0 -1J

·354 智能系统学报 第7卷 Γ000 00 0 2 20-1 0 网络动力学的稳定性分析 0 -1 L= -10 2 -10 0 定理1如果0<(<1/(4m=(G)),则由一阶 00 0 00 0 和二阶多智能体组成的多智能体系统网络是无向连 00-12 0-1 通的或有向平衡连通的,那么P的特征值只有一个 L-10 0 -102 为1,而其他特征值的模均小于1.且 「2 0 -1 -1007 R lim p=w,w. 0 2 -1 -1 00 L= 0 0 0 00 式中:m,=[西,,0,],m=11…1]为mx1 n 0 0 0 00 矩阵,w2=1/Wn11…1]为n2×1为矩阵,w3=1/ 2 0 00 0 200」 √nm[00…0]为n×1矩阵,且w好=1/Wn1+2, Pw.-w,wiP-Wl. -21 5007 证明: 2 -25 00 1)证明如果0<<1/(4m=(G),则矩阵P的 010 特征值的模都小于1.设入:是P的某个特征值,其 0 0 0 1 01 -25 000 相应的特征向量是x:=[号],则有 0 -2g00J P·x:=入:x→ --sL -L2 0. =x -L3 -L40。. (1-L1)x3-gL22=入, 2+=与 图1混合阶智能体的无向网络拓扑结构 -L,-L4x,=A Fig.1 The topology of network with mixed order inte- -(Lx+L2x,)=(入-1)x grator agents 相应的系统动力学方程也变为 =(入:-1)x, (k+1)=P(k). (6) -(Lx+L4x,)= 把L和P做分块展开, rL+L2=(1-)/54, 「L1L21 lL3x+L4,=入(1-入)/g 从以上推导可以得到下面的矩阵方程: 「-L 吃 -L3 -L40n (1-:)/ 0 0 AMaA4 式中:L,0,0n分别是m1×nn×n2n×1 即得 L L2] ,×m矩阵,L=乙,],是多智能体网络拓扑结 4-[A2 0 构对应的Laplacian矩阵.L1、L2、L3、L4是m1×n1、 由这个矩阵方程可知,(1-入:)/化是L的特征 n1Xn2、n2Xn1、n2×n2矩阵. 对于离散时间的变拓扑网络结构,系统的动力 值,而[xx]”是这个特征值所对应的特征向量. 学方程可以重新写为 如果是连通无向图或是连通有向平衡图,那么除了 一个特征值为零外,其余特征根都具有正实部.由圆 5(k+1)=P(k). 盘定理可知 式中:P表示随着切换信号变化而变化的P矩阵 |(1-入:)/g-dm(G)1≤dnm(G)→ l1-入:-gdmm(G)1≤dmm(G)→

第4期 李波,等:离散时间混合多智能体的拟平均一致性控制 ·355· -gdnm(G)≤1-入:-tdnm(G)≤gdma(G)→ 1-gdm.(G)≤入:≤1. ∑0)+∑2((0)+8(0)= 如果要得到1入:1≤1,只需要 (∑0)+∑((0)+(0)®11 0≤(1-dm(G)≤1→ n 0 0≤g≤1/dms(G). 所以, 2)证明1是P的特征值,且其对应的左右特征 = r[50]T,ie{1,2,…,n2}; 向量分别为w,和w, 话,i∈{1,2,…,n1. P=(1/n)1P=(1/历1a=m, 式中:话=(∑(0)+∑2(x(0)+(0)), [11…1]x 这表明,拟平均一致可以达到.证毕. [] √n 定理3令G=(V,e,A)为变拓扑连通加权 Pw,=P =P [11…1]4 =, 无向图或强连通平衡有向图,当0<g<1/dmm(G) n (其中dmm(G)表示变拓扑结构中网络节点的最大 [00…0]d 度),利用协议(5)可以实现拟平均一致. L 证明 从而可知,1是P的特征值. 3)证明R=limP"=w,w成立.则存在一个可 由于0<(<1/dmm(G),则由定理1可知,系 +0 统在k时刻的矩阵P除了有一个特征值为1外,其 逆矩阵S,使得 余特征值的模严格小于1. 时p=之1nP.=1n=研, n √n P.W,=P.[wI w WI]T= 由1)的证明可知,若0<3<1/(4mm(G)),则 1✉ P的特征值除一个为1以外,其余特征值的模均小 于1.因此, [11…1] [W WI WI]T=W √n R limp"lim(SJ S)"=limSJS-= 1 当[00…0]x S-I =S0S- 那么 专”=lim(e)=limP=R(0)=o,07(0)= 0 因为JS=SP,可知S的第一列是,因为S1J= [点11- PS-1,可知S-1的第一行是w.由于SS-1=I,且满 足ew,=1,从而可以得到R=we.证毕. wE(0)= [11…1]23o)= 定理2令G=(V,e,A)为定拓扑连通无向 图,当0<(<1/(4(G))时,应用协议(5)多智能 00…0] n 体网络可以实现拟平均一致. 证明 [11…1]x1] 专·=lim5(t)=limP™=Rξ(0)=,mE(0)= [11…1]x [2点11…1w L[00…0],x n 1[11…1]x ∑0)+2(x(0)+(0)= m2(0)= Σo)+0+o)@l 1[00.0]1 0 也成立,因此协议(5)可是实现拟平均一致证毕. r[11…1]x7 可以得到PI+=1xa+,1+Pm= n [11…1] 11xa+),即∑:(传:(k+1)-专:(k)=0,因而∑ [00…0], 是一个不变量.那么专:可分解为1++8(k)
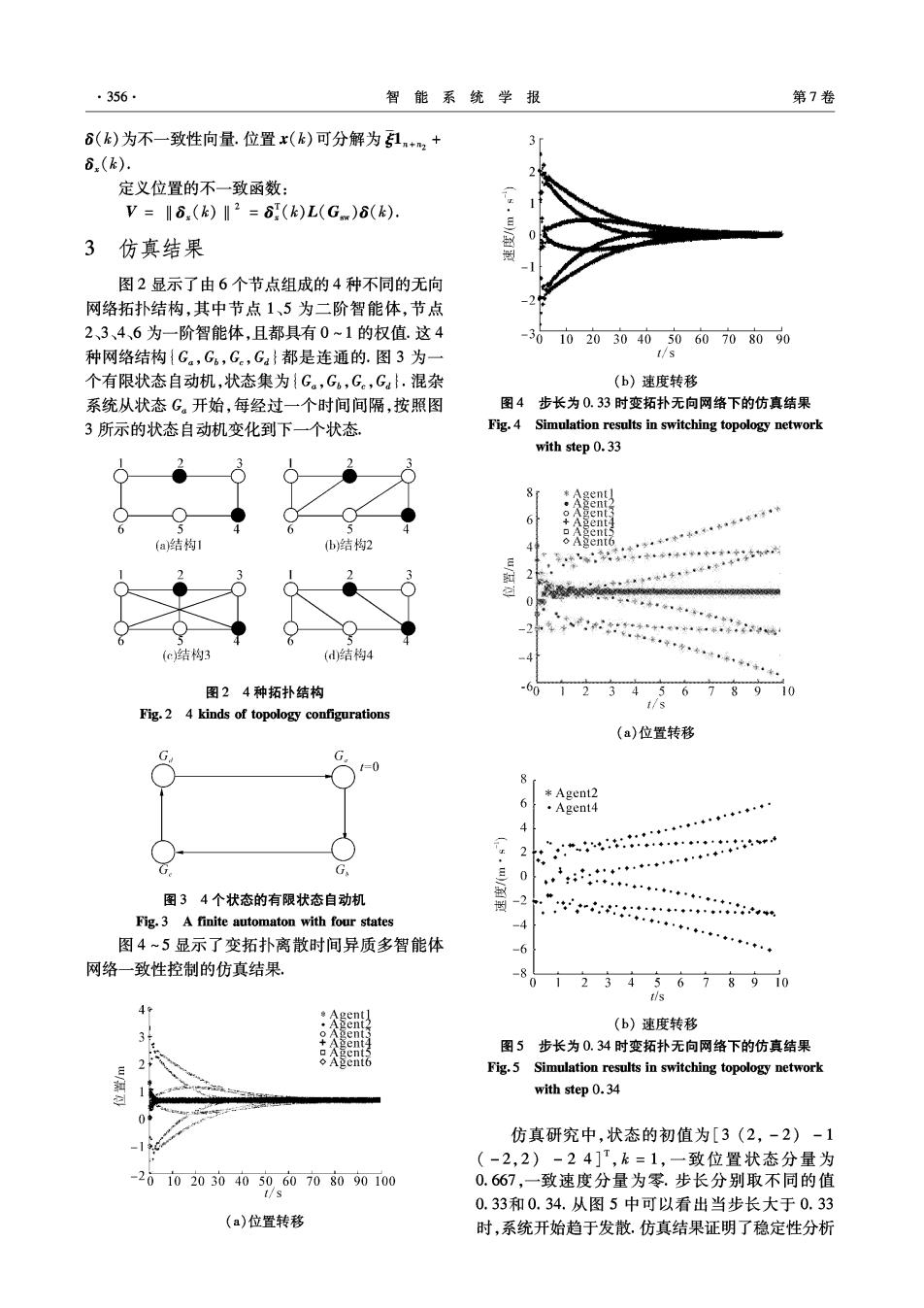
·356 智能系统学报 第7卷 6(k)为不一致性向量.位置x(k)可分解为1+2+ 6.(k). 定义位置的不一致函数: V=I6.(k)‖2=(k)L(G)6(k). 3仿真结果 图2显示了由6个节点组成的4种不同的无向 网络拓扑结构,其中节点1、5为二阶智能体,节点 2、3、4、6为一阶智能体,且都具有0~1的权值.这4 -30102030405060708090 种网络结构{G.,Gb,Ge,Ga}都是连通的.图3为一 t/s 个有限状态自动机,状态集为{Ga,G6,G。,Ga.混杂 (b)速度转移 系统从状态G。开始,每经过一个时间间隔,按照图 图4步长为0.33时变拓扑无向网络下的仿真结果 3所示的状态自动机变化到下一个状态 Fig.4 Simulation results in switching topology network with step 0.33 6 nt (a)结构 b)结构2 2 0 -2… (c结构3 (d)结构4 图24种拓扑结构 -60 12345678910 t/s Fig.2 4 kinds of topology configurations (a)位置转移 G =0 8 t *Agent2 6 … ·Agent4 2+ G G 0 图34个状态的有限状态自动机 Fig.3 A finite automaton with four states -4 ,””◆女*…·◆,。,心◆◆·$ 图4~5显示了变拓扑离散时间异质多智能体 -6 网络一致性控制的仿真结果. -8 01 2345678910 TIs 4 (b)速度转移 图5步长为0.34时变拓扑无向网络下的仿真结果 ◇A2ent6 Fig.5 Simulation results in switching topology network with step 0.34 仿真研究中,状态的初值为[3(2,-2)-1 (-2,2)-24]T,k=1,一致位置状态分量为 -20102030405060708090100 0.667,一致速度分量为零.步长分别取不同的值 I/s 0.33和0.34.从图5中可以看出当步长大于0.33 (a)位置转移 时,系统开始趋于发散.仿真结果证明了稳定性分析

第4期 李波,等:离散时间混合多智能体的拟平均一致性控制 ·357 的正确性。 [8]OLFATI-SABER R,MURRAY R M.Consensus problems in networks of agents with switching topology and time-de- 4结束语 lays[J].IEEE Transactions on Automatic Control,2004, 本文提出了离散时间多智能体系统上的拟平均 49(9):1520-1533. 一致性问题和协议,分析了一致性协议适用的条件, [9]OLFATI-SABER R,FAX JA,MURRAY R M.Consensus and cooperation in networked multi-agent systems[J].Pro- 即如果多智能体系统的网络拓扑结构是连通的且是 ceedings of IEEE,2007,195(1):215-233. 平衡的,并且步长g不大于1/dma(G),那么运用提 [10]LIN P,JIA Y M.Average-consensus in networks of multi- 出的一致性协议,可以使系统达到拟平均一致.并在 agents with both switching topology and coupling time-delay Matlab中仿真了变拓扑无向网络结构的多智能体系 [J].Physica A:Statistical Mechanics and its Applica- 统,步长(分别取0.33、0.34,以及相应的位置不一 tions,2008,348(1):303-313 致函数V=‖δ(k)‖2的曲线.仿真结果证明了理 [11]LIN P,JIA Y M.Consensus control for networks of agents 论分析的有效性。 with double integrator dynamics[EB/OL].[2010-05-12]. http://www.paper.edu.cn. 参考文献: [12 ]LEE D J,SPONG M W.Agreement with non-uniform in- [1]FAX A,MURRAY R M.Information flow and cooperative formation delays[C]//Proceedings of the 2006 American control of vehicle formations[J].IEEE Transactions on Au- Control Conference.Minneapolis,USA,2006:750-756. tomatic Control,2004,49(9):1465-1476. 作者简介: [2]OLFATI-SABER R,MURRAY R M.Distributed coopera- 李波,男,1983年生,主要研究方向 tive control of multiple vehicle formations using structural 为时间自动控制、多智能体一致性控 potential functions [C]//The 15th IFAC World Congress. 制、网络授时. Barcelona,Spain,2002:346-352. [3]REYNOLDS C W.Flocks,herds,and schools:a distribu- ted behavioral model J].ACM SIGGRAPH Computer Graphics,1987,21(4):25-34. [4]CORTES J,BULLO F.Coordination and geometrie optimi- 吴淑琴,女,1972年生,主要研究方 向为卫星通信、数字通信及时间频率应 zation via distributed dynamical systems J].The SIAM 用技术. Journal on Control and Optimization,2006,44(5):1543- 1574. 5]PAGANINI F,DOYLE J,LOW S.Scalable laws for stable network congestion control[C]//Proc of the Int Conf on De- cision and Control.Los Angeles,USA,2001,1:185-190. [6]VICSEK T,CZIROK A,BEN-JACOB E,et al.Novel type 谷明琴,女,1981年生,博士研究 of phase transition in a system of self-driven particles[J]. 生,主要研究方向为多智能体一致性控 Physical Review Letters,1995,75(6):1226-1229. 制、图像处理、模式识别,发表学术论文 [7]JADBABAIE A,LIN J,MORSE S A.Coordination of 多篇. groups of mobile agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control,2003,48(6): 988-1001