
第7卷第5期 智能系统学报 Vol.7 No.5 2012年10月 CAAI Transactions on Intelligent Systems 0ct.2012 D0I:10.3969/i.issn.16734785.201008005 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20120912.1843.002.html 模糊CMAC的柔性空间机器人轨迹跟踪自学习控制 张文辉,周启航2,齐乃明2 (1.丽水学院工学院,浙江丽水323000;2.哈尔滨工业大学航天学院,黑龙江哈尔滨150001) 摘要:针对不确定自由漂浮柔性空间机器人系统,采用模糊CMAC神经网络自学习控制策略来解决轨迹跟踪控制 问题.首先建立漂浮基空间机器人的动力学方程,然后利用具有快速学习能力的模糊CMAC神经网络来逼近非线性 柔性臂的逆动力学模型.网络参数采用改进的有监督的Hbb学习规则进行自适应在线调整,并通过关联搜索进行 自学习和自组织,其误差代价函数由PD控制器提供.仿真结果表明,这种模糊CMAC逆模PD控制器能够达到较 高的控制精度,具有一定的工程应用价值. 关键词:模糊CMAC;逆模控制;柔性空间机器人:PID控制:轨迹跟踪:Hbb学习规则 中图分类号:TP242文献标志码:A文章编号:16734785(2012)05045705 Trajectory tracking self-study control for flexible space manipulators with fuzzy CMAC ZHANG Wenhui',ZHOU Qihang?,QI Naiming? (1.College of Technology,Lishui University,Lishui 323000,China;2.School of Astronautics,Harbin Institute of Technology,Har bin 150001,China) Abstract:Considering the uncertainty of free floating adaptable space robot systems (FSRS),cerebellar model ar- ticulation controller(CMAC)neutral network self-learning control strategies are used to solve the trajectory tracking control problems of the inverse model control algorithm.Firstly,a non-linearity dynamics equation of flexible space ma- nipulator is established.The controller based on fuzzy CMAC neutral network is used for effectively leaming how to com- pensate inverse-model,and fuzzy CMAC network parameters that could be adaptively adjusted online by improved super- visory Hebb leaming rules.Error function is provided via proportional integration differential(PID)controller.The con- troller improved control accuracy and asymptotic convergence of tracking error.The simulation results illustrate the pres- ented controller system has engineering value. Keywords:fuzzy CMAC;inverse-model control;flexible space robot;PID control;trajectory tracking;Hebb learn- ing rules 随着航天运载技术的发展,空间机械臂在大载 应用在机器人跟踪控制中,但应用于空间柔性机器 荷运载方面凸显出极大的优势,其研究也受到专家 人的方法还很少48].由于柔性空间机器人具有更 的广泛关注13].地面机器人和空间机械臂系统均 强的耦合性,其自由漂浮模式下动力学模型难以得 为非线性强耦合系统,但空间机器人相比地面机器 到,采用自适应方法虽可以取得较好的控制效果,但 人而言是非完整动力学系统,机械臂的运动与载体 参数线性化的确定需要大量的计算90.由于模糊 的位姿之间存在着更加强烈的动力学耦合作用及不 控制及神经网络控制不要求知道控制对象的精确模 确定性.为消除这些非线性因素的影响,已有自适应 型,具有学习能力,在空间控制领域的应用取得了一 控制、模糊控制和神经网络控制等先进的控制策略 些成果.其中文献[56]提出了一种模糊控制策略, 模糊规则通过自适应律来调整;但是若存在的模糊 收稿日期:2010-08-21.网络出版日期:2012-09-12 规则过多,计算量将成几何倍数增加,规则过少则不 基金项目:国家自然科学基金资助项目(61171189). 通信作者:张文辉.E-mail:hit_xwh@126.com. 能保证控制精度.文献[7]提出了神经网络的空间

.458 智能系统学报 第7卷 柔性臂控制方案,利用梯度及反向传播误差算法来 在载体姿态为α,机械臂各个关节的相对转角 调整网络权值,该方法存在计算量大、耗时长的缺 0、02及91、92为广义坐标的情况下,设系统的总动 点,难以保证实时性,且由于需要离线训练,因此难 能为T,忽略重力的作用,可认为整个系统的重力势 以应用于复杂的空间环境. 能为零,且柔性机械臂为线弹性变形,故系统总势能 针对以上方法的不足,本文针对柔性空间机械 U等于柔性连杆的弯曲应变能.设均匀弯曲刚度为 臂采用模w糊CMAC(cerebellum model articulation E,由材料力学相关理论,系统的弹性势能为 controller)神经网络自学习控制方案.通过模糊 tu()d (1) CMAC神经网络来快速学习非线性柔性臂的逆动力 学模型,而学习算法采用在线的改进Hbb学习规 系统的拉氏函数为 则,误差调节函数由PD控制器来提供, L=T-U. (2) 联立式(1)~(2)并由拉格朗日方程可得 柔性空间机械臂动力学模型 不失一般性,作平面运动的自由漂浮柔性空间 -斯-0.i=12 (3) 机械臂的系统结构如图1所示.建立平动的惯性坐 式中:L是系统的拉格朗日函数,9:为系统的广义坐 标系O-Y,设各分体沿X-Y平面作平面运动. 标,Q:为广义坐标9:相对应的广义力.不考虑结构 粘性阻尼,结合式(1)~(3),经过推导和整理,可以 得到如下封闭形式的空间刚柔机械臂系统的非线性 动力学方程: D +H= (4) 式中:0=[0102],9=[912],D为4×4的正定对 称广义质量阵,H为4×1的耦合哥氏力、离心力和弹 性力的列阵,x=[:200]T为控制力矩 00 2模糊CMAC神经网络逆模控制器 图1柔性臂漂浮基空间机器人 设计 Fig.1 Model of space robot with flexible manipulator 由于模型比较复杂,不便于进行动力学分析和 2.1模糊CMAC神经网络 控制的研究,所以需要对模型进行合理的假设和近 模糊CMAC神经元网络结合神经网络的学习 似处理.本文只考虑连杆的柔性,同时暂不考虑电机 能力及模糊系统的逻辑认知特性,可实现任意的非 转子的转动惯量和电机的阻尼,在进行系统的动力 线性映射,数学化形式为y=f(x),其中x∈R“为连 学分析时,作如下假设: 续输人空间(N为输人向量维数),y∈N,为输出空 1)各连杆及系统本体的密度分布均匀; 间.其工作机理为:通过对输入的模糊量化,得出输 2)不考虑柔性连杆末端执行器的大小,将其视 入向量激活联想强度的活性,进而激活联想强度以 为集中质量; 恢复系统的信息.以图2所示的双输人单输出模糊 3)连杆的长度远大于其截面尺寸; CMAC为例说明其结构, 4)仅考虑连杆的横向弯曲变形,忽略其轴向变 形和剪切变形等,且假设横向振动为小变形 考虑到B2为柔性杆,在运动过程中必然会发生 变形,由于是细长杆,根据假设,忽略其轴向变形和剪 切变形的影响,将其视为一段Euler-Bernoulli梁进行处 理,柔性梁的弹性位移“的模态函数展开表示为 u(0,)=∑中(x)q.(t),i=1,2,…,n 图2模糊CMAC神经网络结构 式中:中:(x2)为柔性臂第i阶模态函数,9:()为与 Fig.2 FCMAC neural network structure 中:(x2)对应的模态坐标,n为截断项数 1)输人层.第1层的结点是输入结点:

第5期 张文辉,等:模糊CMAC的柔性空间机器人轨迹跟踪自学习控制 ·459· 00=0=x,i=1,2. e+Kae+K,e=D[△Dp+△H]. 式中:)、0分别为第1层第i个神经元的输入 式中:△D=D-D,△H=H-H.由上式可知,系统建 和输出. 模的不确定性会导致控制性能下降. 2)模糊化层.它的每个输人对应n个“块”,这 为解决柔性空间机器人非线性动力学模型的影 里n=2,完成一个输人隶属函数(x:)的计算,则 响,这里考虑采用具有快速逼近能力的FCMAC 输入与块的输入输出关系为 (fuzzy cerebellum model articulation controller)来对 02=I2=g(x),i,j=1,2. 柔性空间机器人的逆动力学模型进行逼近 式中:12、02分别为第2层神经元的输入和输出. 由柔性空间机器人的非线性动力学模型(4)得 3)模糊相联层.该层用于得出输入对联想单元 的激活强度,在输入论域上相对应的“块”组成了22 T =D +H=F(0,0,0,9,9,q) 个超立方体,每个超立方体与一个联想单元相对应, 式中:总控制输人T由PID反馈控制器Tm和 每个联想单元存储着相应的联想强度,输人与各自 FCMAC逆模学习控制器TNN组成, 的隶属关系的“与”操作用乘法来实现: 设计PD反馈控制器为 0=12=0.02. TPID =Kae Kpe. (7) 式中:I、0分别为第3层神经元的输入和输出. FCMAC控制器设计为 4)模糊后相联层.以上层求出的激活强度激活 Tw=M(0,0,0,9,9,9,w). (8) 联想单元中联想强度,则各联想单元中输入输出的 式中:w为FCMAC的连接权值. 关系为: 由式(7)~(8)得总控制律为 =0, T=TPID +TNN. 0g9=1·0g 这里定义FCMAC网络的学习误差E为 式中:I、0分别为各联想单元的输入和输出,0 E=TPID 为各联想单元中存储的联想强度, 采用5层模糊CMAC神经网络为控制器,其隶属函 5)输出层.对于单输出情形,直接给出清晰化 数采用高斯函数: 的输出值: 4(x)=e2,i=1,2,…,6=1,2,…,9. 2 y=∑0. 由于模糊CMAC神经网络只有输出层有权值, 该模糊CMAC中“块”的划分方式和概括程度 且只有与被激活的神经元相连的局部连接权值得到 修正,再由于空间环境的不确定性,离线学习结果很 可以通过隶属函数的参数来在线调整,因此无需在 难适应环境变化.因此,本文采用改进的有监督的 对“块”进行多种方式的划分,超立方体的数量将大 Hbb学习规则,以输出偏差为监督信号,通过关联 大减少,相应的联想单元数量也将大大减少,这不仅 在线搜索进行自学习和自组织,使相应输出增强或 节省了存储空间,同时也大大加快了计算速度, 减弱,以逼近期望输出. 2.2 FCMAC逆模控制器设计 这里采用扩展系统的增广变量输入法,以方便 w:(k+1)=(1-c)w:(k)+r:(k), 应用控制系统模型.定义pa=[0q]T为增广的期 T:(k)=E(k)y(k)x:(k); (9) 望关节角,=[0q]为增广的输入向量,则误差 y()=y(k-1)+k∑0,(k)x, 向量为e=pa-p=[e0],这里eg=0a-a.柔性空 间机器人系统(4)不存在未建模的情况下,下面的 0,(k)= 0:(k) (10) 控制器(5)可以保证系统的稳定性. ∑1w:(k)I T=D(a +Ke +Ke)H. (5) 式中::(k)为递进信号,随过程的进行逐步衰减; 式中:K。、K。为反馈增益矩阵.然而在实际中,空间 E(k)=Tm为输出误差信号;η>0为步长或学习 机器人的模型很难精确得到,只能建立理想的模型。 率;0≤c≤1为正常数. 如果将空间机器人估计模型表示为D、丑,则对于估 联立式(9)~(10)得 计模型的控制律设计为 △0,(k)=-c[o:(k)+”E(k)y(k)x,(k)].(11) T=D(a +KeKe)+H. (6) 将控制律式(6)代入控制律式(5)中,得 式中:△o:(k)=w:(k+1)-w:(k).如果存在函数
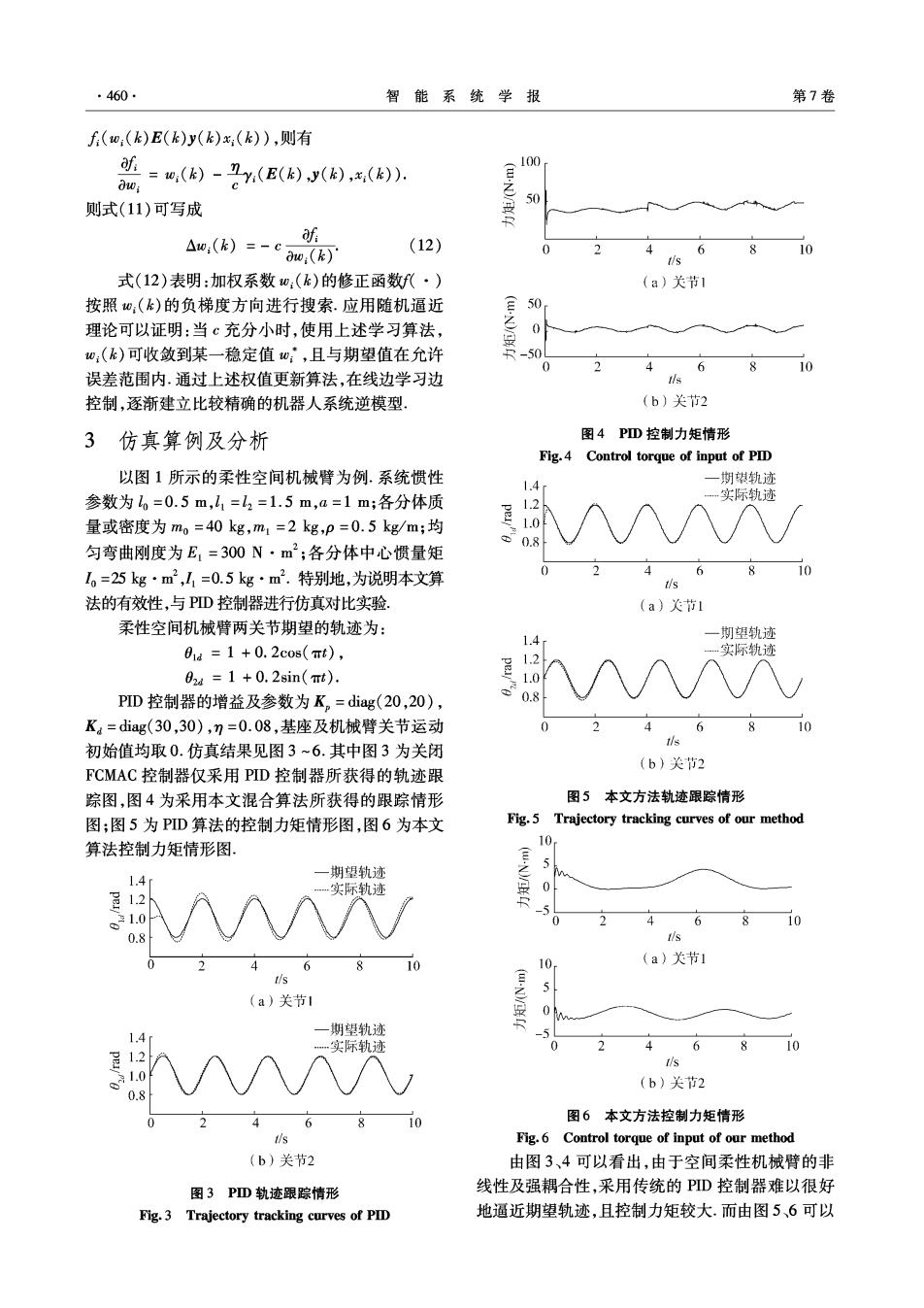
·460. 智能系统学报 第7卷 f(o:(k)E(k)y(k)x:(k)),则有 =o,()-Y(E()J(,(): 100 ow: 则式(11)可写成 50 △0:(k)=-c ow(k)' (12) 0 10 式(12)表明:加权系数w:(k)的修正函数f代·) (a)关节1 按照心:()的负梯度方向进行搜索.应用随机逼近 50 理论可以证明:当c充分小时,使用上述学习算法, 0 0:(k)可收敛到某一稳定值w;,且与期望值在允许 0 4 6 误差范围内.通过上述权值更新算法,在线边学习边 控制,逐渐建立比较精确的机器人系统逆模型, (b)关节2 3仿真算例及分析 图4PD控制力矩情形 Fig.4 Control torque of input of PID 以图1所示的柔性空间机械臂为例.系统惯性 期堪轨迹 1.4 参数为l6=0.5m,l1=l2=1.5m,a=1m;各分体质 1.2 实际轨迹 量或密度为mo=40kg,m1=2kg,p=0.5kg/m;均 1.0 0.8 匀弯曲刚度为E,=300N·m2;各分体中心惯量矩 L=25kg·m,L1=0.5kg·m2.特别地,为说明本文算 4 6 8 10 tis 法的有效性,与PD控制器进行仿真对比实验, (a)关节1 柔性空间机械臂两关节期望的轨迹为: 期望轨迹 1.4 01d=1+0.2cos(πt), 实际轨迹 1.2 02a=1+0.2sin(mrt). 1.0 PID控制器的增益及参数为K。=diag(20,20), 0.8 K。=dig(30,30),n=0.08,基座及机械臂关节运动 4 6 10 初始值均取0.仿真结果见图3~6.其中图3为关闭 (b)关节2 FCMAC控制器仅采用PID控制器所获得的轨迹跟 踪图,图4为采用本文混合算法所获得的跟踪情形 图5本文方法轨迹跟踪情形 图;图5为PD算法的控制力矩情形图,图6为本文 Fig.5 Trajectory tracking curves of our method 算法控制力矩情形图。 10r -期望轨迹 5 1.4 实际轨迹 0 是12 -5 1.0 0 2 4 6 810 0.8 4 6 10 10r (a)关节1 (a)关节l 期望轨迹 1.4 实际轨迹 4 6 10 1.2 8 ts 1.0 (b)关节2 0.8 4 6 8 10 图6本文方法控制力矩情形 s Fig.6 Control torque of input of our method (b)关节2 由图3、4可以看出,由于空间柔性机械臂的非 图3PD轨迹跟踪情形 线性及强耦合性,采用传统的PD控制器难以很好 Fig.3 Trajectory tracking curves of PID 地逼近期望轨迹,且控制力矩较大.而由图5、6可以

第5期 张文辉,等:模糊CMAC的柔性空间机器人轨迹跟踪自学习控制 ·461· 看出,所设计的基于FCMAC的逆模PD控制器能 控制研究[J].宇航学报,2008,29(6):1865-1869, 在较短时间t=1s内快速跟踪期望轨迹,且整个过 ZHANG Xiaodong,JIA Qingxuan,SUN Hanxu,et al.The 程控制力矩不大.这是由于本文方法在控制过程的 research of space robot flexible joint trajectory control[J] 开始阶段,神经网络未能比较精确逼近机器人逆模 Joumal of Astronautics,2008,29(6):1865-1869. 型时,与常规PD反馈控制器共同作用,以满足关节 [7]洪在地,负超,陈力.漂浮基空间机器人及其柔性影响下 逆模神经网络控制[J].宇航学报,2007,28(6):1510- 角的轨迹跟踪.神经网络的学习需要一定的时间,但 1514. 考虑到空间机器人为了保持基体姿态,通常运动很 HONG Zaidi,YUN Chao,CHEN Li.Inverse model neuron 慢,这为神经网络的学习提供了足够的时间,可以满 control of free floating space robot with rigid manipulators 足实时要求 and rigid flexible manipulators[J].Journal of Astronautics. 4结束语 2007,28(6):1510-1514. [8]张文辉,齐乃明,尹洪亮.自适应神经变结构的机器人轨 针对不确定性柔性自由漂浮空间机器人系统的 迹跟踪控制[J].控制与决策,2011,26(4):597-600. 轨迹跟踪控制问题,本文采用模糊CMAC神经网络 ZHANG Wenhui,QI Naiming,YIN Hongliang.Neural- 自适应控制方法.该方法利用模糊CMAC神经网络 variable structure-based adaptive trajectory tracking control of robot manipulators[J].Control and Decision,2011,26 来逼近逆动力学模型,通过改进的有监督的Hebb (4):597-600. 学习规则来进行参数的学习,避免了离线学习阶段, [9]YOSHIDA K,HASHIZUME K,ABIKO S.Zero reaction 加快了学习速度,误差代价函数由PD控制器提供, maneuver:flight validation with ETS-VII space robot and 从而达到了自学习和自组织的目的,仿真结果表明 extension to kinematically redundant arm[C]//Proceedings 了所提方案的有效性。 of the IEEE Intemational Conference on Robotics and Auto- mation.Seoul,Korea,2001:441446. 参考文献: [10]CHEN Li.Adaptive and robust composite control of coordi- [1]ABDOLLAHI F,TALEBI H A,PATEL R V.A stable neu- nated motion of space robot system with prismatic joint ral network-based observer with application to flexible-joint [C]//Proceedings of the 4th World Congress on Intelligent manipulators[J].IEEE Transactions on Neural Networks, Control and Automation.Shanghai,China,2002,2: 2006,17(1):118-129. 1255-1259, [2]张文辉,齐乃明,尹洪亮.自由漂浮空间机器人神经网络 作者简介: 自适应补偿控制[J].宇航学报,2011,32(6):1312 张文辉,男,1980年生,讲师,博士, 1317. 主要研究方向为机器人动力学与控制, ZHANG Wenhui,QI Naiming,YIN Hongliang.Neural net- 发表学术论文20余篇. work adaptive compensation control of free-floating space ro- bot[J].Journal of Astronautics,2011,32(6):1312- 1317. [3]HU H,WOO P Y.Fuzzy supervisory sliding-mode and neu- ral-network control for robotic manipulators[J].IEEE 周启航,男,1987年生,硕士研究 Transactions on Electronics,2006,53(3):929-940. 生,主要研究方向为机器人动力学与 [4]张文辉,齐乃明,李运迁.基于模糊基函数网络的机械臂 控制。 免模型输出反馈PD控制[J].国防科技大学学报, 2010,32(6):163-170 ZHANG Wenhui,QI Naiming,LI Yunqian.Output feed- back PD control of robot manipulators dispense with model based on fuzzy-basis-function-network [J].Journal of Na- 齐乃明,男,1962年生,教授,博士 tional University of Defense Technology,2010,32(6): 生导师,主要研究方向为空间动力学与 163-170. [5]GREEN A,SASIADEK J Z.Adaptive control of a flexible 控制、微重力环境模拟等,发表学术论 文70余篇: robot using fuzzy logic[J].AIAA Journal of Guidance, Control and Dynamics,2005,28(1):36-42. [6]张晓东,贾庆轩,孙汉旭,等.空间机器人柔性关节轨迹