
第7卷第3期 智能系统学报 Vol.76.3 2012年6月 CAAI Transactions on Intelligent Systems Jun.2012 D0I:10.3969/i.issn.16734785.201012018 网络出版地址:htp://www.cnki.net/kcms/detail/23.1538.TP.20120423.1518.001.html 单喷泵无人滑行艇航向的反步自适应滑模控制 廖煜雷,庄佳园,庞永杰1,杜鑫2 (1.哈尔滨工程大学水下智能机器人技术国防科技重点实验室,黑龙江哈尔滨150001;2.总参陆航研究所,北京100020) 摘要:针对单泵喷水推进型无人滑行挺航向跟踪的非线性系统控制问题,对无人滑行艇的运动稳定性分析表明, 其具有水平面内的自动稳定性.考虑建模误差和外界干扰力影响下的滑行艇运动响应模型,基于backstepping方法 和滑模控制理论,提出了一种自适应滑模控律.利用Lyapunov函数,证明该控制律保证了航向跟踪系统的全局渐 近稳定性.仿真对比结果验证了所提出控制器的有效性. 关键词:单泵喷水推进器;无人滑行艇;航向控制;滑模控制;backstepping法 中图分类号:TP273;U664文献标志码:A文章编号:16734785(2012)03-0246-05 Backstepping adaptive sliding mode control for an unmanned planning craft course system with single waterjet LIAO Yulei,ZHUANG Jiayuan',PANG Yongjie',DU Xin2 (1.National Key Laboratory of Science and Technology on Autonomous Underwater Vehicle,Harbin Engineering University,Harbin 150001,China;2.Army Aviation Institute,Beijing 100020,China) Abstract:The course-tracking nonlinear control problem of an unmanned planning craft with single waterjet was ad- dressed in this paper.Based on motion stability analysis of the unmanned planning craft,the system had automatic stability on the horizontal plane.Considering the motion response model affected by of the modeling errors and ex- ternal disturbances,an adaptive sliding mode control law was proposed via the sliding mode control theory and backstepping method.By means of the Lyapunov function,it was proven that the proposed control law can render the course-tracking system globally asymptotically stable at the origin.Simulations results illustrate the effectiveness of the proposed method. Keywords:single waterjet;unmanned planning craft;course control;sliding mode control;backstepping method 无人水面艇(unmanned surface vehicle,USV),是控制)、现代鲁棒控制2]、滑模变结构控制3]、 一种自主式的无人水面小型船舶.文中USV是装备 Backstepping法[4]、基于人工智能S]和以上方法的 单泵喷水推进器的刚性充气滑行艇.在不同航速下, 混合控制策略等[6).在USV控制方面,YU等将鲁 艇体的浸湿面积和吃水等会发生很大变化,其艇体各 棒控制方法应用到USV的艏向控制中89],文献 种水动力系数也将随航速的变化而改变,故该USV [10]基于Lyapunov直接法设计了三体型USV的速 具有强非线性、不确定性和时变性的特点,同时受风 度控制器,Bao等针对USV的艏向和横向控制问 浪流等海洋环境干扰力的影响较大,要建立其精确的 题,基于滑模观测器和滑模控制器设计了艏向和横 USV动力学模型非常困难,因此,控制算法必须能够 向联合控制器1,文献[l2]利用Lyapunov直接法 适应被控制系统模型参数的变化.作为自主航行的水 和Backstepping方法设计了USV的速度和艏向联合 面智能体,航向控制问题尤为突出,设计具有自适应 控制器. 性的自动驾驶操舵系统显得非常重要。 本文讨论了USV在未知不确定性影响下的航 当前船舶航向的非线性控制方法主要有自适应 向跟踪控制问题.首先分析了USV的自动稳定性, 然后基于Backstepping法和滑模控制理论,提出了 收稿日期:2010-12-25.网络出版日期:2012-04-23. 一种自适应滑模反馈控制律,该控制律能保证航向 基金项目:国家自然科学基金资助项目(50909025/E091002);中国博 士后科学基金资助项目(20080440838). 跟踪系统的全局渐近稳定性,其优点在于具有较短 通信作者:鹰煜雷.E-mail:liaoyulei@hheu.edu.cm 的收敛时间、良好的动态性能和自适应能力.理论分

第3期 廖煜雷,等:单喷泵无人滑行挺航向的反步自适应滑模控制 ·247· 析和仿真对比试验皆表明了文中控制律的正确性和 内的直线自动稳定性,习惯上也常称为航向稳定性, 有效性, 与常规水面船舶相比,如“育龙”号实习船四 中,K=-0.48、T=216.8,文中USV的T值较小,因 1系统描述和运动稳定性分析 此具有较好的稳定性;而K较大,因此回转性能也 1.1滑行艇操纵运动数学模型 更好.可见该艇具有良好的机动性能,这是由艇型和 考虑到在大舵角下运动和不稳定船舶的操纵特 操舵方式决定的,即USV动力装置为喷水推进器, 性,Bech等在二阶线性K-T方程的基础上,进一步 它通过改变喷嘴转角来进行艏向控制(对喷嘴转角 发展了非线性响应方程,形成二阶非线性艏摇响应 的操纵,按习惯称为舵角操纵). 方程: 显然,USV航向跟踪控制系统(2)、(3)是单输 T,T2r+(T1+T2)r+r+r3=K6+KT3&. 入单输出的不确定性非线性系统,控制问题可描述 (1) 为设计反馈控制律,保证USV的艏向跟踪误差有界 式中:「是艏摇角速度(顺时针为正),8为控制舵角 且收敛到零 (左舵为正),T、T、T3为时间常数,K为回转性指 数,a为模型非线性项系数(Norbbin系数). 在操舵不是很频繁的情况下,考虑建模误差和 外界干扰力等非匹配不确定性的影响,船舶航向非 线性操纵系统可以采用以下的一阶非线性艏摇响应 方程(2): Tr +r+ar'K6+TF (2) 式中:T为时间常数;F为建模误差△和未知外界干 图1.试验中的USV 扰力ω的不确定性总和,即F=△(业,山)+ω,假设 Fig.1 Unmanned surface vessel operating in the sea 不确定性的上界为|F1≤F,且为慢变过程P=0. 2反步自适应滑模控制器 USV艏向角业与艏摇角速度r的关系为 d=r. (3) 2.1反步自适应滑模控制器设计 1.2航向稳定性分析 首先,定义如下状态变换: 2010年5月,该USV在山东省蓬莱海域进行了 r1=中-中a, 大量的直航、回转和Z型机动等操纵性试验,如图1 X=c11, 所示.对试验数据进行系统辨识得到了艇体的水动 2=1+X=r+c-a 力系数,文中的USV操纵性参数分别为K= 式中:山为期望艏向角,满足二阶可导的光滑函数; -2.364、T=5.489、T1=6.255、T2=0.331. X为稳定项辅助方程;C1为正常数. 船舶在水平面内的航向稳定性包括自动稳定性 定义Lyapunov预选函数为 和控制稳定性3 首先研究自动稳定性,忽略式(1)的非线性项, 以= 其特征方程式为 对V,求导,则 TT2A2+(T1+T2)x+1=0. (4) V1=2-c1. 式(4)的2个特征根入1、入2可按韦达定理求得 定义Lyapunov预选函数为 1 A:=-元,入2=-石 %=+2 为了判断水平面的自动稳定性,只需判断特征方 式中:σ为滑模切换函数.定义切换函数为 程(4)的根的符号,而并不需要解方程式的根.采用古 0=k11+2 尔维茨判别法,式(4)的两根都具有负实部的充要条 式中:k为正常数.对V2求导,则 件是方程式的系数全部大于零,即 2=1+0G=-c1i+312+ 「TT2>0, o[k(a2-ca1)+f+b6+F+X-a].(5) LT1+T2>0. 式中:f=-r/T-ar3/T,b=K/T. 也即要求T1>0,T2>0.因为T=6.255>0,T2= 取反馈控制律为 0.331>0,由古尔维茨判别法可知,该USV具有水平面 6=b-[a-k(2-ca1)-f-

248. 智能系统学报 第7卷 Fsgm(o)-X-h(σ+Bsgm(σ)]. (6) 法设计USV航向跟踪控制器,其中假设不确定性 式中:hB皆为正常数.将式(6)代入式(5)可得 F=0. 2≤-C12+12+ 引入如下2个误差变量: Il (I FI-F)-ho2-hBlls 「x1=中-中a, (14) -c+zz-ho2-hBI ol. (7) l2=r-ψa-n 取矩阵 式中:7=-n11为虚拟控制输入,n1为正常数, -g“: 定义Lyapunov预选函数为 (8) 飞=品 (15) 由于 对式(15)求导可得V4=-n1x2+x12:如果2=0, 则V,≤0,为此需要进行下一步设计.定义Lyapunov 预选函数为 (c1+h)异+(2hk1-1)z+hz. (16) 式中:Z=[a12]T.则当121=h(c1+k)-1/4>0 %=%+2起 时,式(7)有 对式(16)求导可得 2≤-ZQz-hB1ol≤0. 3=-n1x+x1x2+x2(f+b6-a-7) 那么只要选取适当的h、c1、k1使得IQ1>0,从而保 为使V,≤0,设计反馈控制律为 证2为正定矩阵,则必有2≤0成立.也就保证了 8=b(a+7-f-x1-n2) .(17) USV航向跟踪系统是Lyapunov意义下全局渐近稳 式中:2为正常数,将控制律(14)代入式(13)可得 定的. V3=-n1x-n2x号≤0. 在实际控制中,USV航态复杂多变,因此具有 由设计过程可知,系统满足Lyapunov稳定性理 强非线性,这导致航向非线性系统的模型参数很难 论条件,因此误差变量1、x2是渐近稳定的,这保证 精确获得且具有较大不确定性;同时,USV航行于 了USV航向跟踪系统是全局渐近稳定的. 复杂海洋环境中,经常受到未知外加干扰力的影响 2.3稳定性分析 因此,总不确定性F的上界很难确定,为了避免F 由上面的设计过程可知,Backstepping法是一种 上界带来的抖振等问题,采用自适应算法对F进行 由前向后递推的设计方法,通过逐步迭代设计Lya 估计4 punov函数使系统的误差渐近稳定,最终实现对原 设F为F的估计值,估计误差F=F·-F,定义 系统的全局渐近镇定. Lyapunov预选函数为 定理1考虑存在不确定性影响的航向非线性 系统(2)、(3),在自适应反馈控制律(11)和不确定 g=+岁产 (9) 性自适应控制律(12)的作用下,误差变量1、2、0 式中:y为正常数.对式(9)求导可得 是全局渐近稳定的,保证了USV航向跟踪系统的全 乃=-c+-F(市-y0)+ 局渐近稳定性,实现了航向的自适应控制, 证明由2.1节的设计过程得证. o[k(a2-c1a1)+f+b6+F+X-a].(10) 定理2在反馈控制律(17)的作用下,误差变 设计自适应反馈控制律为 量x1x2全局渐近收敛到零,即USV状态误差满足 8=b[边a-k,(a2-c1a1)-f- liml中-中al=liml业-中al=0,这保证了USV航向 F-X-h(σ+Bsgm(o)]. 跟踪控制系统是全局渐近稳定的, (11 定义不确定性F的自适应律为 证明由2.2节的设计过程得证. F=yo. (12) 3仿真结果与分析 将式(11)和(12)代入式(10),且由式(8)可得 根据海试操纵性试验结果,文中USV操舵系统的 3=-cz号+aa-ha2-hglσl= 参数为K=-2.364、T=5.489、=0.000094.为了方便 -ZQz-hB1o|≤0. (13) 阐述,反步自适应滑模控制器称为控制律1,Backstep 2.2 Backstepping控制器设计 pig控制器称为控制律2.控制律1的设计参数为c1= 为了与文中自适应反步(Backstepping)滑模控 0.9、k1=0.15、h=0.26B=0.002、y=0.0001.控制律2 制器的控制效果进行对比,下面利用Backstepping 的设计参数为n1=0.03、n2=7
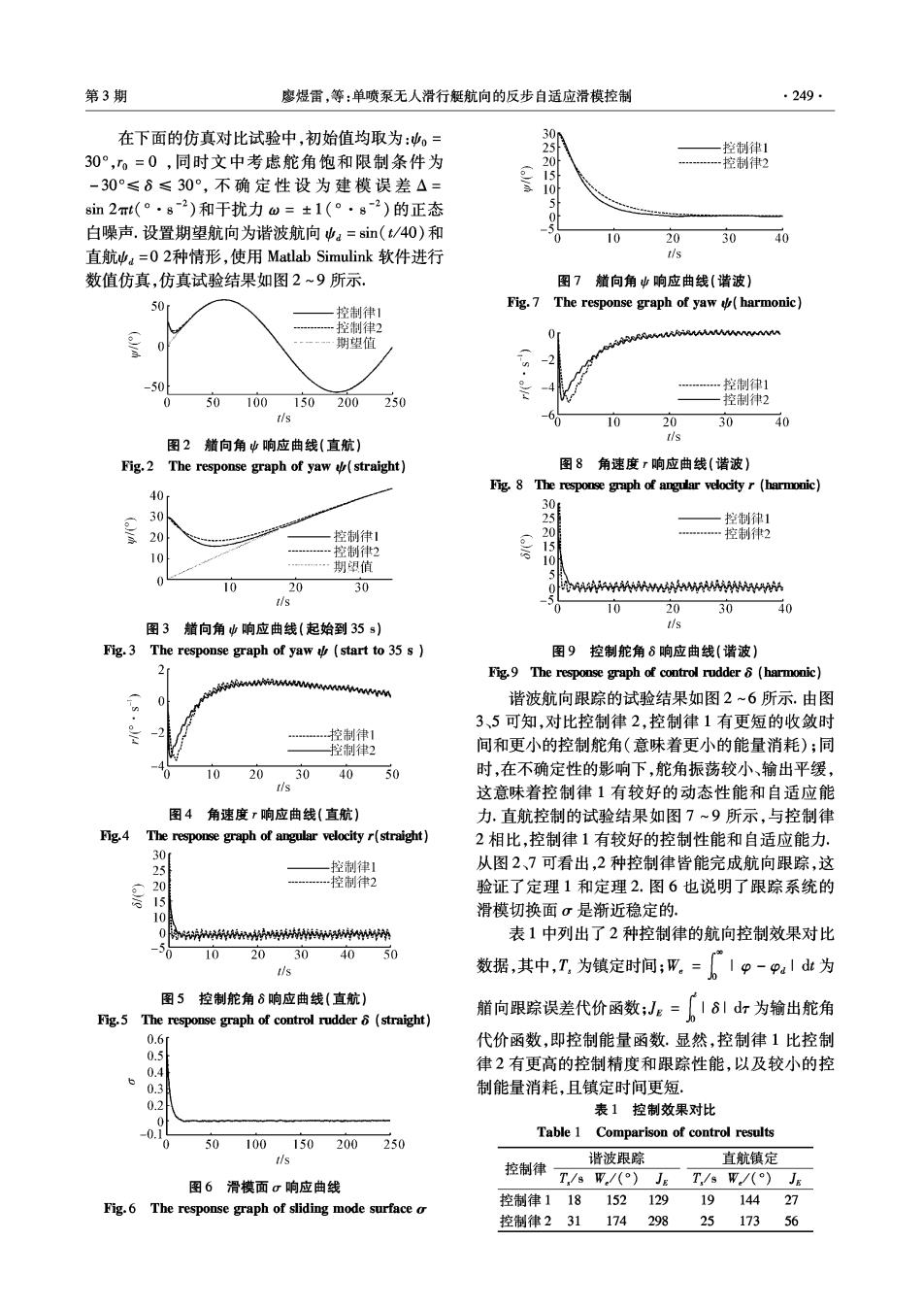
第3期 廖煜雷,等:单喷泵无人滑行艇航向的反步自适应滑模控制 ·249· 在下面的仿真对比试验中,初始值均取为:,= 30 拦制律1 30°,0=0,同时文中考虑舵角饱和限制条件为 控制律2 -30°≤6≤30°,不确定性设为建模误差△= 10 8in2t(°·82)和千扰力w=±1(。·82)的正态 505 白噪声.设置期望航向为谐波航向中a=sin(t/40)和 0 10 20 30 40 直航a=02种情形,使用Matlab Simulink软件进行 tis 数值仿真,仿真试验结果如图2~9所示. 图7艏向角中响应曲线(谐波) Fig.7 The response graph of yaw (harmonic) 控制律1 -控制律2 0 期望值 50 …控制律1 50 100150200 250 -控制律2 t/s 10 20 30 tis 图2艏向角业响应曲线(直航) Fig.2 The response graph of yaw (straight) 图8角速度r响应曲线(谐波)】 Fig.8 The respouse graph of angular velocityr (harmonic) 40 30 30 一控制律1 20 控制律1 20 …控制律2 10 一…控制律2 期望值 10 10 20 30 50 WWwNMW tis 10 20 30 40 图3艏向角山响应曲线(起始到35s) Fig.3 The response graph of yaw (start to 35 s 图9控制舵角8响应曲线(诸波) 2 Fig.9 The respouse graph of control rudder (harmonic) 0 谐波航向跟踪的试验结果如图2~6所示.由图 3、5可知,对比控制律2,控制律1有更短的收敛时 控制律1 一制律2 间和更小的控制舵角(意味着更小的能量消耗);同 10 2030 40 50 时,在不确定性的影响下,舵角振荡较小、输出平缓, 这意味着控制律1有较好的动态性能和自适应能 图4角速度,响应曲线(直航) 力.直航控制的试验结果如图7~9所示,与控制律 Fig.4 The response graph of angular velocityr(straight) 2相比,控制律1有较好的控制性能和自适应能力. 30 5 控制律1 从图2、7可看出,2种控制律皆能完成航向跟踪,这 20 控制律2 验证了定理1和定理2.图6也说明了跟踪系统的 15 10 滑模切换面σ是渐近稳定的. 片Mwwwwww 表1中列出了2种控制律的航向控制效果对比 -5 10 20304050 tis 数据,其中,工为镇定时间:网.=19-1d业为 图5控制舵角6响应曲线(直航) Fig.5 The response graph of control rudder 6 (straight) 艏向跟踪误差代价函数;。=厂I61dr为输出舵角 0.6 代价函数,即控制能量函数.显然,控制律1比控制 0.5 0.4 律2有更高的控制精度和跟踪性能,以及较小的控 0.3 制能量消耗,且镇定时间更短 0.2 表1控制效果对比 0 -0 Table 1 Comparison of control results 0 50100150200250 谐波跟踪 控制律 直航镇定 图6滑模面σ响应曲线 T./s W/()JE T,/s W/()JE 控制律118152129 1914427 Fig.6 The response graph of sliding mode surface o 控制律231174 298 2517356

·250 智能系统学报 第7卷 4 结束语 CAAI Transactions on Intelligent Systems,2010,5(4): 308-312. 文中讨论了在模型不确定性和外界干扰下, [8]YU Z,BAO X,NONAMI K.Course keeping control of an USV航向非线性系统的控制问题.对试验数据的分 autonomous boat using low cost sensors[J].Journal of Sys- 析表明,该USV在水平面内运动是静不稳定的,但 tem Design and Dynamics,2008,2(1):389-400. 具有运动稳定性,基于滑模控制理论和Backstepping [9]YU Z,BAO X,NONAMI K.Mixed H,/H based course following control for a small low cost autonomous boat[]. 法,提出了一种反步自适应滑模控制器.通过理论证 ICGST International Journal on Automatic Control and Sys- 明,在该控制律作用下USV的航向跟踪控制系统是 tems Engineering,2007,7(1):51-59. 全局渐近稳定的.数值仿真对比试验表明所提控制 [10]KUMARAWADU S,KUMARA K J C.On the speed con- 律具有良好的自适应性和跟踪性能,该方法也可推 trol for automated surface vehicle operation [C]//The 广到其他海洋运载系统.探讨更复杂环境下的航向 Third Interational Conference on Information and Automa- 控制问题,将是未来的研究重点, tion for Sustainability.Melbourne,Australia,2007:135- 140. 参考文献: [11]BAO X,NONAMI K,YU Z.Combined yaw and roll con- trol of an autonomous boat[C]//2009 IEEE International [1]SKJETNEA R,FOSSEN T I,KOKOTOVIC P V.Adaptive Conference on Robotics and Automation.Kobe,Japan, maneuvering,with experiments,for a model ship in a ma- 2009:188-193. rine control laboratory [J].Automatica,2005,41(2): [12]LIAO Yulei,PANG Yongjie,WAN Lei.Combined speed 289-298. and yaw control of underactuated unmanned surface vehi- [2]HU SS,YANG P H,JUANG J Y,et al.Robust nonlinear cles[C]//The 2nd International Asia Conference on Infor- ship course keeping control by H 1O linearization and u- matics in Control,Automation and Robotics.Wuhan,Chi- synthesis[J].International Joumal of Robust and Nonlinear na,2010:157-161. Control,2002,13(1):55-70. [13]范尚雍.船舶操纵性[M].北京:国防工业出版社, [3]刘雨,郭晨,吕进.基于backstepping的船舶航向滑模控 2002:30-39. 制[J].中南大学学报:自然科学版,2007,38(增刊1): [14]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清 278-279 华大学出版社,2002:240-247. LIU Yu,GUO Chen,LU Jin.Sliding-mode control of ship course tracking based on backstepping[J].Joumal of Cen- 作者简介: tral South University:Science and Technology,2007,38 廖煜雷,男,1985年生,博士研究 (suppl.1):278-279. 生,主要研究方向为USV基础运动控制 [4]朱齐丹,周芳,赵国良,等.基于反步法和滑模观测器的 和欠驱动船舶运动控制,发表学术论文 船舶航向控制[J].华中科技大学学报:自然科学版, 10余篇. 2009,37(4):122-125. ZHU Qidan,ZHOU Fang,ZHAO Guoliang,et al.Control of ship courses using backstepping and sliding mode observ- er[J].Joural of Huazhong University of Science and Tech- nology:Natural Science Edition,2009,37(4):122-125. 庄佳园,男,1984年生,博士研究 「5]汪洋,郭晨,孙富春,等.基于动态神经模糊算法的船舶 生,主要研究方向为水面USV路径规划 航向自适应控制[J].哈尔滨工程大学学报,2009,30 和运动控制· (10):1159-1164. WANG Yang,GUO Chen,SUN Fuchun,et al.Adaptive control of ship course using a dynamic neural fuzzy algorithm [J].Journal of Harbin Engineering University,2009,30 (10):1159-1164 [6]罗伟林,邹早建,李铁山.船舶航向非线性系统鲁棒跟踪 庞永杰,男,1955年生,教授,博士 控制[J].控制理论与应用,2009,26(8):893-895. 生导师,第3、4届海洋工程学会理事, LUO Weilin,ZOU Zaojian,LI Tieshan.Robust tracking 主要研究方向为水下机器人总体设计 control of nonlinear ship steering[J].Control Theory Ap- 与运动控制技术.目前主持和参与省部 plications,2009,26(8):893895. 级以上科研项目多项,获得国家科技进 [7]袁雷,吴汉松.船舶航向非线性系统的多滑模自适应模 步二等奖1次,国防科学技术一、二、三 糊控制[J].智能系统学报,2010,5(4):308-312 等奖各1次,发表学术论文50余篇, YUAN Lei,WU Hansong.Multiple sliding mode adaptive fuzzy controller for nonlinear marine autopilot systems[J]