
第7卷第5期 智能系统学报 Vol.7 No.5 2012年10月 CAAI Transactions on Intelligent Systems 0ct.2012 D0I:10.3969/i.issn.16734785.201207029 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20120924.1551.001.html 基于自适应差分进化的干线交通信号协调控制 毕晓君,刘国安,肖婧 (1.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001:2.辽宁省交通高等专科学校信息工程系,辽宁 沈阳110122) 摘要:为克服现有基于传统智能优化算法的城市干线交通信号协调控制方法求解特度低、易陷入局部最优等缺 陷,将改进后的动态自适应差分进化算法P-ADE应用于城市干线双向交通信号的协调优化控制,通过优化干线交叉 路口相位差减小交通流平均延误.PADE在标准差分进化算法基础上提出了新变异策略和参数动态自适应调整策 略,有效平衡算法的局部搜索与全局搜索能力.通过与基于多种群免疫算法等协调优化控制方法对比,实验结果表 明,p-ADE在收敛精度、速度和鲁棒性上相比较于多种先进智能优化算法均具有明显优势,可以为交通干线系统提 供更优的相位差,有效减少干线直行交通流的平均延误,提高城市主干道交通通行能力. 关键词:差分进化;智能交通;干线协调控制;P-ADE;多种群免疫算法 中图分类号:TP18文献标志码:A文章编号:16734785(2012)05043707 Coordination and control of arterial traffic signals based on adaptive differential evolution BI Xiaojun',LIU Guoan',XIAO Jing (1.College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China:2.Department of Infor- mation Engineering,Liaoning Provincial College of Communications,Shenyang 110122,China) Abstract:In order to improve the efficiency and stability of the coordination and control on urban arterial traffic sig- nal of traditional intelligent optimization algorithms,and to avoid flaws such as low precision solution and local opti- ma,a dynamic self-adaptive differential evolution algorithm,named p-ADE,will be examined.In the p-ADE,a new mutation strategy and a self-adaptive parameter adjustment technique are proposed to balance local and global searches for the improvement on convergence accuracy and speed.Experimental outcome illustrates the p-ADE al- gorithm outperformed several state-of-the-art optimization algorithms.In addition,innovative coordination control methods are capable of offering better traffic signal patterns that can reduce the average delay of traffic flow.This new technology will ultimately help improve the traffic capacity of urban trunk road traffic. Keywords:differential evolution;intelligent transportation;arterial coordination and control;pbest-based adaptive differential evolution (p-ADE);multi-population immunity algorithm 城市交通干线作为城市道路交通网中的主动脉 制方法(定时控制、多时段控制等)很难对其进行有 往往承受着巨大的交通负荷,提高干线上交通信号 效控制,因此将具有非线性、自组织、自寻优等特点 的协调控制能力,减少干线交通延误和停车率,对于 的智能控制技术引入城市道路交通控制是一个必然 改善区域甚至整个城市的交通状况具有重大意 趋势u].近年来,遗传算法(genetic algorithm, 义[].由于城市交通系统本身是一个具有强非线 CA)1、免疫算法(immune algorithm,IA)Is1、粒子 性、随机性、时变性和不确定性的复杂系统,传统控 群优化算法(particle swarm optimization,PS0)[8]等 智能优化技术已广泛应用于城市道路交通单交叉路 收稿日期:201207-18.网络出版日期:201209-24. 口信号控制最优化问题,并取得了一定的成果;但求 基金项目:国家自然科学基金资助项目(61175126);教育部博士点基 金资助项目(20112304110009):中央高校基本科研业务费 解线控、面控系统信号控制最优协作等复杂问题时 重大项目培育计划资助项目(HEUCFZ1209). 仍然存在易陷入局部最优、求解精度差等问题,无法 通信作者:刘国安.E-mail:liuguoan@hrbeu.edu.cn

·438. 智能系统学报 第7卷 为交通控制系统提供最优的信号协调控制方案,没 中的最优解,X则是从第i个个体在第t代之前 有从根本上解决城市道路交通问题. 的所有父代个体、变异个体和试验个体(交叉后个 针对以上问题,在智能优化算法差分进化(df 体)之中选择出的历史最优解.该变异策略中将目 ferential evolution,DE)的基础上进行改进,提出了 标个体的历史最优解X引入变异操作中,用X 一种基于新变异策略的动态自适应差分进化算法 与当前解的差值向量代替原差分向量,引导目标个 (pbest-based adaptive differential evolution,p-ADE), 体向着更优的方向进化,同时利用当前种群全局最 进一步提升了DE算法的求解精度及鲁棒性.将P 优解X加强个体的局部搜索能力,通过随机选择 ADE用于城市于线双向交通信号的协调优化控制, 个体X,保证种群多样性,防止陷入局部最优, 通过优化干线交叉口相位差获得最佳的平均延误. 1.2新参数动态自适应调整策略 实验中将p-ADE与多种群免疫算法(multi--popula- 控制参数大小的设置及调整方法对DE算法的 tion immune algorithm,MLA)[6进行对比,测试结果 性能有重要影响.P-ADE中所涉及的主要控制参数 表明,PADE算法优化结果能够获得更小的干线直 有W,、K、F,:和CRi,,为达到最佳性能采用动态 行交通流平均延误,且具有更强的稳定性. 的参数自适应调整方式,即根据进化代数和种群个 1 基于新变异策略的动态自适应差分 体的优劣差异对每个个体进行动态自适应调整.首 进化算法 先,算法在进化初期增强个体的局部搜索能力和种 群探索能力,而进化后期增强个体的全局搜索能力 差分进化DE是目前最前沿、最具代表性、性能 和种群的开采能力;其次,群体中适应度较差的个 最优的进化算法之一,但仍然存在易陷入局部最优、 体,加大其变异程度,即在变异、交叉过程中引入更 搜索具有一定盲目性、控制参数难以设定等问 多的扰动,加强其向更优搜索方向变化.参数调整具 题911.大量实验结果表明,DE算法的性能高度依 体操作如式(2)~(5)所示: 赖于优化策略(包含变异策略和交叉策略)及相应 W,=Win+(Wnar-Wma)X 参数的选择[91o.现有大多数DE及其改进算法的 变异策略中,通常采用随机的方式从种群中选择个 (2) 体构成差分矢量,对目标个体的搜索方向引入过多 K,t=Kia+(Knma-Ka)义 的随机性干扰信息,导致目标个体可能出现偏离甚 至背离全局最优解搜索方向的情况,使得新产生的 ((oxp(xhn2) -1 2 +×分》 (3) 子代个体的质量大大降低,同时迭代次数的增加也 Ft=fia+((Fma-Fia)X 降低了算法的收敛速度. 针对这一问题,本文提出了新的DE变异策略 ,(4) DE/rand-to-best/pbest和新的参数自适应调整策略, CR,it=CR,in+(CR,mr-CR,min)× 构成了一种综合改进的差分进化算法PADE,以提 升DE算法的全局优化能力. (5) 1.1新DE变异策略DE/rand-to-best/pbest 式中:f,为第t代种群中第i个个体的适应度值, 进化算法的核心问题在于如何平衡算法的探索 ∫m,和∫m血分别为第t代种群中个体的最大适应度 与开发能力,加强探索能力有助于提高算法的可靠 值和最小适应度值,参数的变化范围为W,∈ 性,而加强开发能力可以提高搜索效率,一般来说二 [0.1,0.9],K∈[0.3,0.9],F∈[0.3,0.9]和 者之间存在矛盾.为了达到平衡,P-ADE采用随机 CRe[0.1,0.9]8.所有参数的调整同时考虑了 选择的方式选取基向量,以保持种群良好的多样性. 进化代数以及个体适应度值的影响,在自身取值范 在此基础上为提高搜索效率,利用种群最优解个体 围内动态自适应地变化,无需人为干预和任何先验 等优秀个体提供优秀解分布区域的搜索方向性指 知识 导.基于这一思想提出DE变异策略DE/rand-to- best/pbest,具体形式如式(1)所示. 2自适应差分进化在城市干线协调优 V,:=W,Xt+K(Xet,4-X,)+ 化控制中的应用 F.(X.). (1) 2.1城市干线交通协调优化控制模型 式中:X,为随机选择的基向量;Xt是第t代种群 采用基于最小延误的常态交通条件下干线双向绿

第5期 毕晓君,等:基于自适应差分进化的干线交通信号协调控制 ·439· 波控制模型,如图1所示.该线控系统由s1,2,…,5m共 响,线控系统上、下行车速分别为v,和va(km/h).线控 n个交叉口组成,交叉口之间的距离分别为1,l2,…, 系统内部交通流为非饱和流,保证绿波控制得以实施, 1n-·线控系统各路段车道数和车道宽均一致,上、下行 周期长和绿信比用传统方法确定,通过调节交叉口相 交通量分别为q.和qa(veh/h),不考虑转弯车辆的影 位差实现干线车辆延误最小化 交叉口s, 交叉口s」 交叉口s 交叉口8 wqio u292 442*9n2 uns4on 交叉口s, 交叉口s 交叉口s, 交叉口s 交叉口s 交叉口s 上行延误 下行延误 上行延误 下行延误 上行延误 下行延误 图1干线双向交通绿波控制模型 Fig.1 Green wave control model of two-way arterial traffic 忽略干线系统外部进道口$1和sn驶人车流产 式中:=1对应车辆在红灯启亮时刻到达,a:=0 生的延误,中间交叉口则须考虑上、下行车辆延误,使 对应车辆在红灯启亮后到达, 线控系统车辆延误最小,即使各交叉口延误之和最小 干线交通中上行车辆通过交叉口延误的计算方 下行车辆通过交叉口延误的计算方法如下:对 法与下行车辆类似,相邻交叉口s:相对于3:+1的信 于交叉口s+1,由s:下行的车辆行驶时间为l/a,车 号相位差为p,+1=T-p+1i,即相邻两交叉口相互 辆由:下行至s+1的延误分为2种情况:一种是车 之间的相位差之和为一个周期.若上行车辆恰好在 辆到达:+1时恰好红灯启亮,车辆受阻导致延误;另 红灯启亮时由s:+1行至:,则其对应延误为 一种情况是车辆到达+1时信号灯已经变为红灯, 9.us 车辆受阻导致延误, d.=2(.-q) 对于第1种情况,假设从车队头部到达s+1至 式中:9为周期内s:交叉口的上行交通量,“为周 s:+1红灯结束的车辆等待时间为,一个周期中交叉 期内绿灯期间s:交叉口的最大通行能力.若上行车 口红灯时长为t,则有t,=t.s+1相对于s:的信号相 辆在红灯启亮后由s+行至s,则其对应延误为 位差为+1,如式(6)所示,其中T为系统周期. 2 ](mod T)q.u. [4](modT)+t:=9+1 (6) 2(4。-9a) 周期内下行车队在交叉口$+1的延误值为 由此得到上行车辆在干线所有交叉口产生的总 Eqaua 延误为 d(+a=2(w4-9a) D. ∑[B,du+(1-B,)d]. 式中:qa为周期内s+1的下行交通量,u为周期内绿 式中:B,=1对应车辆在红灯启亮时刻到达,B=0 灯期间+1的最大通行能力.第2种情况下t≠t, 对应车辆在红灯启亮后到达,根据干线交通车辆上、 因此周期内下行车队在交叉口s+的延误值为 下行延误D.、Da,得到整个线控系统交叉口的延误 tqaua 之和D=Da+D da=2(wa-qa 2.2基于pADE的干线信号协调优化控制 12 利用p-ADE算法对干线交通信号动态优化控 制模型进行求解,通过优化干线双向交通交叉口的 2(ua-9d) 相位差P,使沿干线行驶车辆延误之和D达到最小, 由前述2种情况可知,下行车辆在干线所有交 具体操作步骤如下(如图2). 叉口产生的总延误为 1)建立干线系统交通信号协调优化模型, Da=∑[a,da+(1-a)da]. 2)根据系统上、下行交通量、车速等参数确定 2 系统的周期长和绿信比
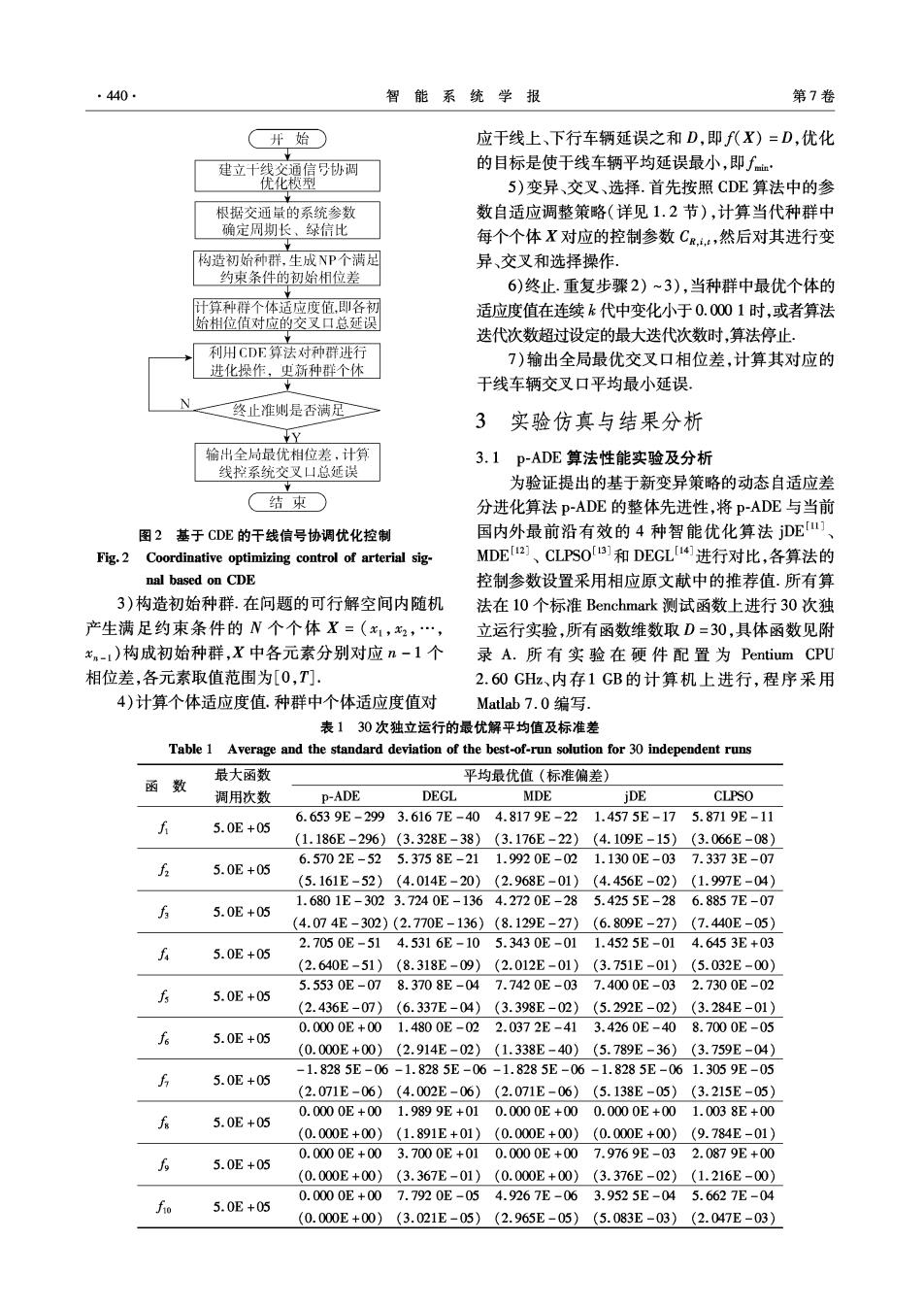
·440. 智能系统学报 第7卷 井始 应干线上、下行车辆延误之和D,即f(X)=D,优化 建立十线交通信号协调 的目标是使干线车辆平均延误最小,即f 优化榄型 5)变异、交叉、选择.首先按照CDE算法中的参 根据交通量的系统参数 数自适应调整策略(详见1.2节),计算当代种群中 确定周期长、绿信比 每个个体X对应的控制参数CR,,然后对其进行变 构造初始种群,生成NP个满足 异、交叉和选择操作 约束条件的初始相位差 6)终止.重复步骤2)~3),当种群中最优个体的 计算种群个体活应度值,即各初 适应度值在连续k代中变化小于0.0001时,或者算法 始相位值对应的交叉口总延误 迭代次数超过设定的最大迭代次数时,算法停止, 利用CDE算法对种群进行 7)输出全局最优交叉口相位差,计算其对应的 进化操作,史新种群个休 干线车辆交叉口平均最小延误。 终止淮则是否满足 3实验仿真与结果分析 Y 输出全局最优相位差,计算 3.1p-ADE算法性能实验及分析 线控系统交叉口总延误 为验证提出的基于新变异策略的动态自适应差 结束○ 分进化算法p-ADE的整体先进性,将p-ADE与当前 图2基于CDE的干线信号协调优化控制 国内外最前沿有效的4种智能优化算法DEu1 Fig.2 Coordinative optimizing control of arterial sig- MDE2]、CLPS0[a]和DEGL14进行对比,各算法的 nal based on CDE 控制参数设置采用相应原文献中的推荐值.所有算 3)构造初始种群.在问题的可行解空间内随机 法在l0个标准Benchmark测试函数上进行30次独 产生满足约束条件的N个个体X=(x1,2,…, 立运行实验,所有函数维数取D=30,具体函数见附 x.-1)构成初始种群,X中各元素分别对应n-1个 录A.所有实验在硬件配置为Pentium CPU 相位差,各元素取值范围为[0,T]. 2.60GHz、内存1GB的计算机上进行,程序采用 4)计算个体适应度值.种群中个体适应度值对 Matlab7.0编写. 表130次独立运行的最优解平均值及标准差 Table 1 Average and the standard deviation of the best-of-run solution for 30 independent runs 最大函数 函数 平均最优值(标准偏差) 调用次数 P-ADE DEGL MDE jDE CLPSO 6.6539E-2993.6167E-404.8179E-221.4575E-175.8719E-11 5.0E+05 (1.186E-296)(3.328E-38)(3.176E-22)(4.109E-15)(3.066E-08) 6.5702E-525.3758E-211.9920E-021.1300E-037.3373E-07 5.0E+05 (5.161E-52)(4.014E-20)(2.968E-01)(4.456E-02)(1.997E-04) 1.6801E-3023.7240E-1364.2720E-285.4255E-286.8857E-07 5.0E+05 (4.074E-302)(2.770E-136)(8.129E-27)(6.809E-27)(7.440E-05) 2.7050E-514.5316E-105.3430E-011.4525E-014.6453E+03 f 5.0E+05 (2.640E-51)(8.318E-09)(2.012E-01)(3.751E-01)(5.032E-00) 5.5530E-078.3708E-047.7420E-037.4000E-032.7300E-02 5.0E+05 (2.436E-07)(6.337E-04)(3.398E-02)(5.292E-02)(3.284E-01) 0.0000E+001.4800E-022.0372E-413.4260E-408.7000E-05 5.0E+05 (0.000E+00)(2.914E-02)(1.338E-40)(5.789E-36)(3.759E-04) -1.8285E-06-1.8285E-06-1.8285E-06-1.8285E-061.3059E-05 5.0E+05 (2.071E-06)(4.002E-06)(2.071E-06)(5.138E-05)(3.215E-05) 0.0000E+001.9899E+010.0000E+000.0000E+001.0038E+00 5.0E+05 (0.000E+00)(1.891E+01)(0.000E+00)(0.000E+00)(9.784E-01) 6 0.0000E+003.7000E+010.0000E+007.9769E-032.0879E+00 5.0E+05 (0.000E+00)(3.367E-01)(0.000E+00)(3.376E-02)(1.216E-00) 0.0000E+007.7920E-054.9267E-063.9525E-045.6627E-04 5.0E+05 (0.000E+00)(3.021E-05)(2.965E-05)(5.083E-03)(2.047E-03)
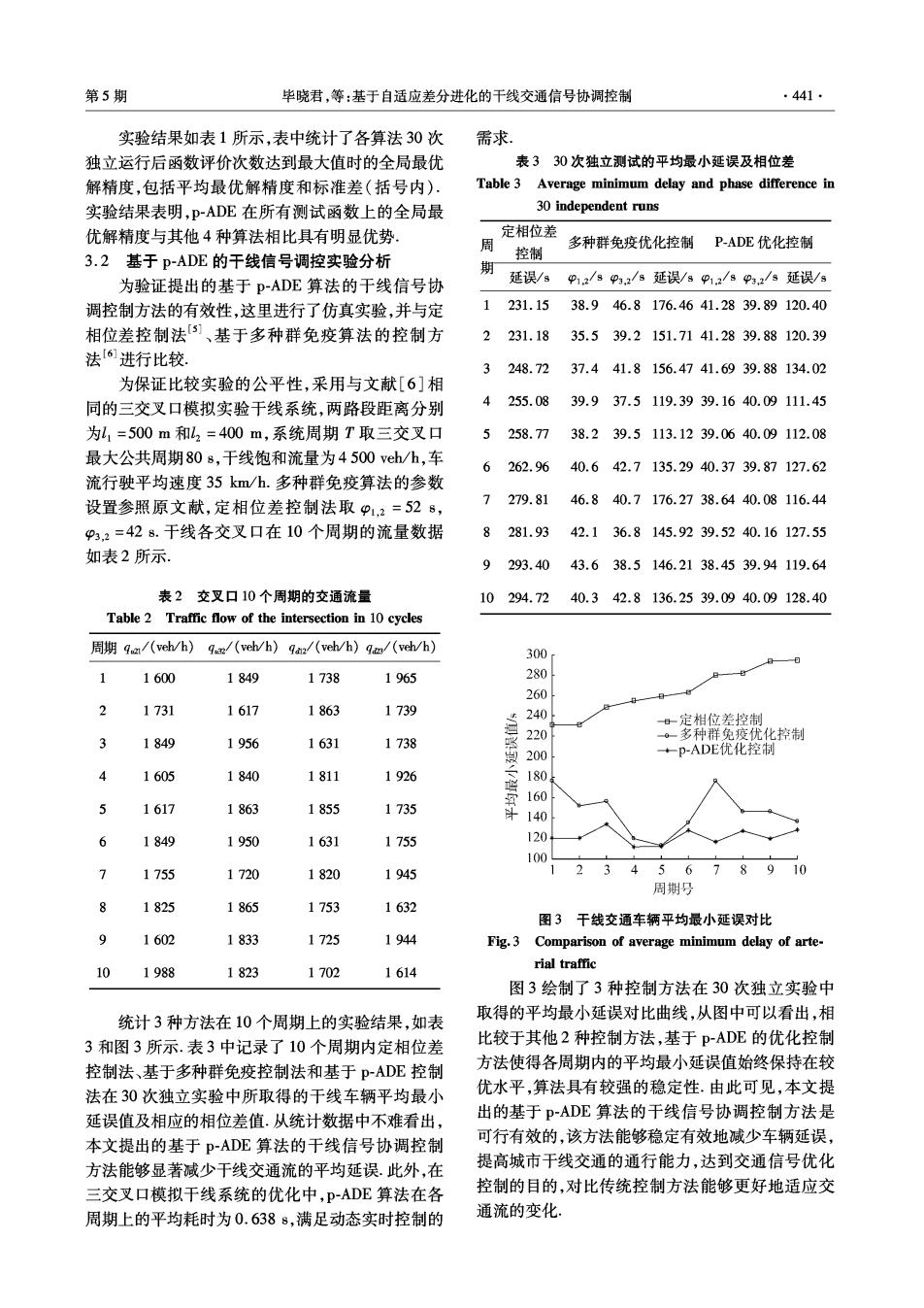
第5期 毕晓君,等:基于自适应差分进化的干线交通信号协调控制 .441 实验结果如表1所示,表中统计了各算法30次 需求 独立运行后函数评价次数达到最大值时的全局最优 表330次独立测试的平均最小延误及相位差 解精度,包括平均最优解精度和标准差(括号内)· Table 3 Average minimum delay and phase difference in 实验结果表明,PADE在所有测试函数上的全局最 30 independent runs 优解精度与其他4种算法相比具有明显优势 定相位差 周 多种群免疫优化控制P-ADE优化控制 3.2基于P-ADE的干线信号调控实验分析 控制 期 为验证提出的基于P-ADE算法的干线信号协 延误/8p1.2/sp3,2/s延误/sp1.2/8P3,2/s延误/s 调控制方法的有效性,这里进行了仿真实验,并与定 1231.15 38.946.8176.4641.2839.89120.40 相位差控制法]、基于多种群免疫算法的控制方 2231.1835.539.2151.7141.2839.88120.39 法[6进行比较. 3 248.7237.441.8156.4741.6939.88134.02 为保证比较实验的公平性,采用与文献[6]相 同的三交叉口模拟实验干线系统,两路段距离分别 4255.0839.937.5119.3939.1640.09111.45 为l1=500m和L2=400m,系统周期T取三交叉口 5 258.7738.239.5113.1239.0640.09112.08 最大公共周期80s,干线饱和流量为4500veh/h,车 6262.9640.642.7135.2940.3739.87127.62 流行驶平均速度35km/h.多种群免疫算法的参数 设置参照原文献,定相位差控制法取P1,2=528, 7279.81 46.840.7176.2738.6440.08116.44 p3,2=428.干线各交叉口在10个周期的流量数据 8281.9342.136.8145.9239.5240.16127.55 如表2所示。 9 293.4043.638.5146.2138.4539.94119.64 表2交叉口10个周期的交通流量 10294.72 40.342.8136.2539.0940.09128.40 Table 2 Traffic flow of the intersection in 10 cycles 周期qa/(veh/h) qa/(veh/h)9an/(veh/h)ga/(veh/h) 300 1 1600 1849 1738 1965 280 260 2 1731 1617 1863 1739 240 定相位差控制 220 。多种群免疫优化控制 3 1849 1956 1631 1738 200 +p-ADE优化控制 4 1605 1811 1926 180 160 161 186 855 1735 140 1755 120 100 1945 5678910 周期号 1825 1865 1753 1632 图3干线交通车辆平均最小延误对比 9 1602 1833 1725 1944 Fig.3 Comparison of average minimum delay of arte- 10 1988 1823 1702 1614 rial traffic 图3绘制了3种控制方法在30次独立实验中 统计3种方法在10个周期上的实验结果,如表 取得的平均最小延误对比曲线,从图中可以看出,相 3和图3所示.表3中记录了10个周期内定相位差 比较于其他2种控制方法,基于P-ADE的优化控制 控制法、基于多种群免疫控制法和基于p-ADE控制 方法使得各周期内的平均最小延误值始终保持在较 法在30次独立实验中所取得的干线车辆平均最小 优水平,算法具有较强的稳定性.由此可见,本文提 延误值及相应的相位差值.从统计数据中不难看出, 出的基于p-ADE算法的干线信号协调控制方法是 本文提出的基于P-ADE算法的干线信号协调控制 可行有效的,该方法能够稳定有效地减少车辆延误, 方法能够显著减少干线交通流的平均延误.此外,在 提高城市干线交通的通行能力,达到交通信号优化 三交叉口模拟干线系统的优化中,P-ADE算法在各 控制的目的,对比传统控制方法能够更好地适应交 周期上的平均耗时为0.6388,满足动态实时控制的 通流的变化

·442. 智能系统学报 第7卷 向交通信号的协调优化控制中获得更优的交通流平 4 结束语 均最小延误.通过与其他协调优化控制方法对比,实 针对现有基于传统智能优化算法(如遗传算 验结果表明,P-ADE算法在收敛精度和鲁棒性上均 法、免疫算法等)的城市干线交通信号协调优化控 具有明显优势,为城市干线交通信号协调控制提供 制方法效率低、稳定性差、易陷入局部最优等问题, 了新的方法和思路.然而,本文研究的干线交通系统 提出了一种动态自适应差分进化算法PADE,通过 信号协调控制在实际应用中还存在覆盖范围上的局 改进DE算法的变异策略和参数动态自适应调整策 限性,因此下一步的研究方向为智能化的区域交通 略提高算法的收敛精度和速度,从而在城市干线双 流信号控制. 附录A 表A1测试函数集 Table Al Test functions sets 函 数 数学表达公式 D 初始化范围 最优值 Sphere function -2 30 -100≤x:≤100 方(0)=0 f:Schwefel's problem 1.2 (四=含(名 30 -100≤x,≤100 f6(0)=0 High conditioned elliptic function 0-名(10)起 30 -100≤x:≤100 f6(0)=0 f:Schwefel's problem 1.2 =宫(宫x1+040 30 -100≤¥,≤100 f(0)=0 with noise Noisy quadratic function 6(=左时+amd[0,l) 30 -1.28≤x≤1.28f6(0)=0 Griewank's function -名高-)1 30 0≤,:≤600 f6(1)=0 -0a-a2B含 f方:Ackley's function 30 -32≤x:≤32 f(0)=0 (合om(220+ Rastrigin's function i)=2(传-10cs(2)+10y 30-5.12≤x:≤5.12f(0)=0 5(x=足(传-10e(2)+10. Noncontinuous Rastrigin's iflx:1 <0.5; 30-5.12≤x≤5.12f6(0)=0 function else. 国-2(套don(en+os)- Weierstrass function D宽[dcos(2mx0.5)l, 30 -0.5≤x:≤0.5fio(0)=0 a=0.5,b=3,k=20 参考文献: LI Xiaohong.Urban arterial traffic signal coordination con- trol and simulation[D].Dalian:Institute of Technology of [1]李晓红.城市干线交通信号协调优化控制及仿真[D].大 Dalian,2007:22-47. 连:大连理工大学,2007:22-47. [2]陈小锋.城市交通信号动态优化控制技术研究[D].西

第5期 毕晓君,等:基于自适应差分进化的干线交通信号协调控制 ·443· 安:西北工业大学,2003:2556. [10]PRICE K,STORN R M,LAMPINEN J A.Differential e- CHEN Xiaofeng.Research on dynamic optimization and volution:a practical approach to global optimization[M] control techniques for urban traffic signal[D].Xian:North- Berlin,Germany:Springer-Verlag,2005. western Polytechnical University,2003:25-56 [11]吴亮红.差分进化算法及应用研究[D].长沙:湖南大 [3]王东.城市干线交通信号协调控制研究[D].西安:长安 学,2007:2489.WU Lianghong.The research and appli- 大学,2010:2866 cation of differential evolution algorithm[D].Changsha: WANG Dong.The study of urban arterial traffic signal coor- Hunan University,2007:24-89. dination control based on genetic algorithm[D].Xi'an: [12]ZAHARIE D.Critical values for the control parameters of Changan University,2010:28-66. differential evolution algorithms[C]//Proceedings of the [4]沈国红.城市道路交通智能控制技术研究[D].杭州:浙 8th Interational Conference on Soft Computing.Bro, 江大学,2004:33-58. Czech Republic,2002:62-67. SHEN Guohong.A study on intelligent control technique for [13]LAMPINEN J,ZELINKA I.On stagnation of the differen- urban traffic[D].Hangzhou:Zhejiang University,2004: tial evolution algorithm[C]//Proceedings of the 6th Inter- 33-58. national Conference on Soft Computing.Bro,Czech Re- [5]朱晓燕.城市干线交通流仿真研究及软件设计[D].南 public,2000:76-83. 京:东南大学,2005:2568. [14]FAN Huiyuan,LAMPINEN J.A trigonometric mutation ZHU Xiaoyan.Simulation research and software design of operation to differential evolution[J].Joumal of Global urban trunk road traffic flow[D].Nanjing:Southeast Uni- 0 ptimization,2003,27(1):105-129. versity,2005:2568. 作者简介: [6]徐建伟.基于免疫算法的城市干线交通信号协调控制研 毕晓君,女,1964年生,教授,博士生 究[D].湘潭:湘潭大学,2008:2186. 导师,博士.主要研究方向为智能信息处 XU Jianwei.Urban arterial traffic signal coordination control 理、智能优化算法理论及应用.先后承担 research based on immune algorithm[D].Xiangtan:Xiang- “十一·五”预研项目、国家自然科学基金 tan University,2008:21-86. 项目以及省部级科研项目12项,曾获省 [7]顾榕,曹立明,王小平.基于改进免疫遗传算法的交通信 部级科学技术进步二等奖3项、三等奖4 号优化控制[J].模式识别与人工智能,2006,19(3): 项.发表学术论文51篇,其中被检素23篇、SP检紫5篇, 331-337. 出版专著3部,获国家发明专利授权1项. GU Rong,CAO Liming,WANG Xiaoping.The optimization for traffic signal based on improved immune genetic algo- 刘国安,男,1983年生,助理研究员, rithm[J].Pattem Recognition and Artificial Intelligence, 博士研究生,主要研究方向为智能优化算 2006,19(3):331-337. 法理论及应用.参与国家自然科学基金项 [8]李乐,史忠科.基于遗传算法改进的交通干线信号优化 目1项,发表学术论文5篇,其中被EI检 研究[J].计算机仿真,2009,26(1):260-263. 索4篇. LI Le,SHI Zhongke.Traffic trunk road signal optimization based on an improved genetic algorithm[J].Computer Sim- ulation,2009,26(1):260-263. 肖婧,女,1985年生,讲师,博士,主要 [9]付绍昌,黄辉先,肖业伟,等.自适应变异粒子群算法在 研究方向为智能信息处理、智能优化算法 交通控制中的应用[J].系统仿真学报,2007,19(7): 理论及应用.承担辽宁省教育厅项目1 1562-1564,1612. 项、辽宁省科技厅博士科研启动基金项目 FU Shaochang,HUANG Huixian,XIAO Yewei,et al.Ap- 1项,发表学术论文7篇,其中被SCI检索 plication of adaptive mutation-particle swarm optimization al- 2篇、E检索4篇. gorithm in traffic control[J].Joumnal of System Simulation, 2007,19(7):15621564,1612