
《概率论与数理统计》课程教学大纲 一、课程信息 课程名称:概率论与数理统计 Probability and Statistics 课程代码: 课程类别:专业拓展平台课程/选修课 适用专业:工程管理专业 课程学时:54学时 课程学分:2学分 修读学期:第3学期 先修课程:高等数学A(I)、高等数学A(I) 二、课程目标 (一)具体目标 通过本课程的学习,使学生达到以下目标: 课程目标1:掌握概率论基本概念,包括频率、概率、古典概型、条件概率等概 念及运算方法,会使用全概率公式以及贝叶斯公式进行计算,并能分析变量之间的独 立性;掌握离散型随机变量的分布律分布函数,包括两点分布、二项分布的分布律 分布函数:掌握连续型随机变量的概率密度包括均匀分布、指数分布、正态分布:掌 握二维随机变量边缘分布函数的定义以及边缘概率密度的计算方法。【支撑毕业要求 11】 课程目标2:掌握数学期望、方差、协方差、相关系数的计算方法;熟悉辛钦大 数定律、伯努利大数定律的使用:掌握独立同分布的中心极限定理、李雅普诺夫定理 以及棣莫弗-拉普拉斯定理的使用;掌握样本和抽样分布相关概念,能利用直方图与 箱线图解决问题;掌握矩估计量、矩估计值、似然函数、最大似然估计值、最大似然 估计量、对数似然方程的定义:熟悉假设检验相关知识,能使用正态总体均值的假设 检验。【支撑毕业要求2.1】 (二)课程目标与毕业要求的对应关系 表1课程目标与毕业要求的对应关系 1
——1—— 《概率论与数理统计》课程教学大纲 一、课程信息 课程名称:概率论与数理统计 Probability and Statistics 课程代码: 课程类别:专业拓展平台课程/选修课 适用专业:工程管理专业 课程学时:54学时 课程学分:2学分 修读学期:第3学期 先修课程:高等数学A(I)、高等数学A(II) 二、课程目标 (一)具体目标 通过本课程的学习,使学生达到以下目标: 课程目标 1:掌握概率论基本概念,包括频率、概率、古典概型、条件概率等概 念及运算方法,会使用全概率公式以及贝叶斯公式进行计算,并能分析变量之间的独 立性;掌握离散型随机变量的分布律分布函数,包括两点分布、二项分布的分布律、 分布函数;掌握连续型随机变量的概率密度包括均匀分布、指数分布、正态分布;掌 握二维随机变量边缘分布函数的定义以及边缘概率密度的计算方法。【支撑毕业要求 1.1】 课程目标 2:掌握数学期望、方差、协方差、相关系数的计算方法;熟悉辛钦大 数定律、伯努利大数定律的使用;掌握独立同分布的中心极限定理、李雅普诺夫定理 以及棣莫弗-拉普拉斯定理的使用;掌握样本和抽样分布相关概念,能利用直方图与 箱线图解决问题;掌握矩估计量、矩估计值、似然函数、最大似然估计值、最大似然 估计量、对数似然方程的定义;熟悉假设检验相关知识,能使用正态总体均值的假设 检验。【支撑毕业要求 2.1】 (二)课程目标与毕业要求的对应关系 表1 课程目标与毕业要求的对应关系
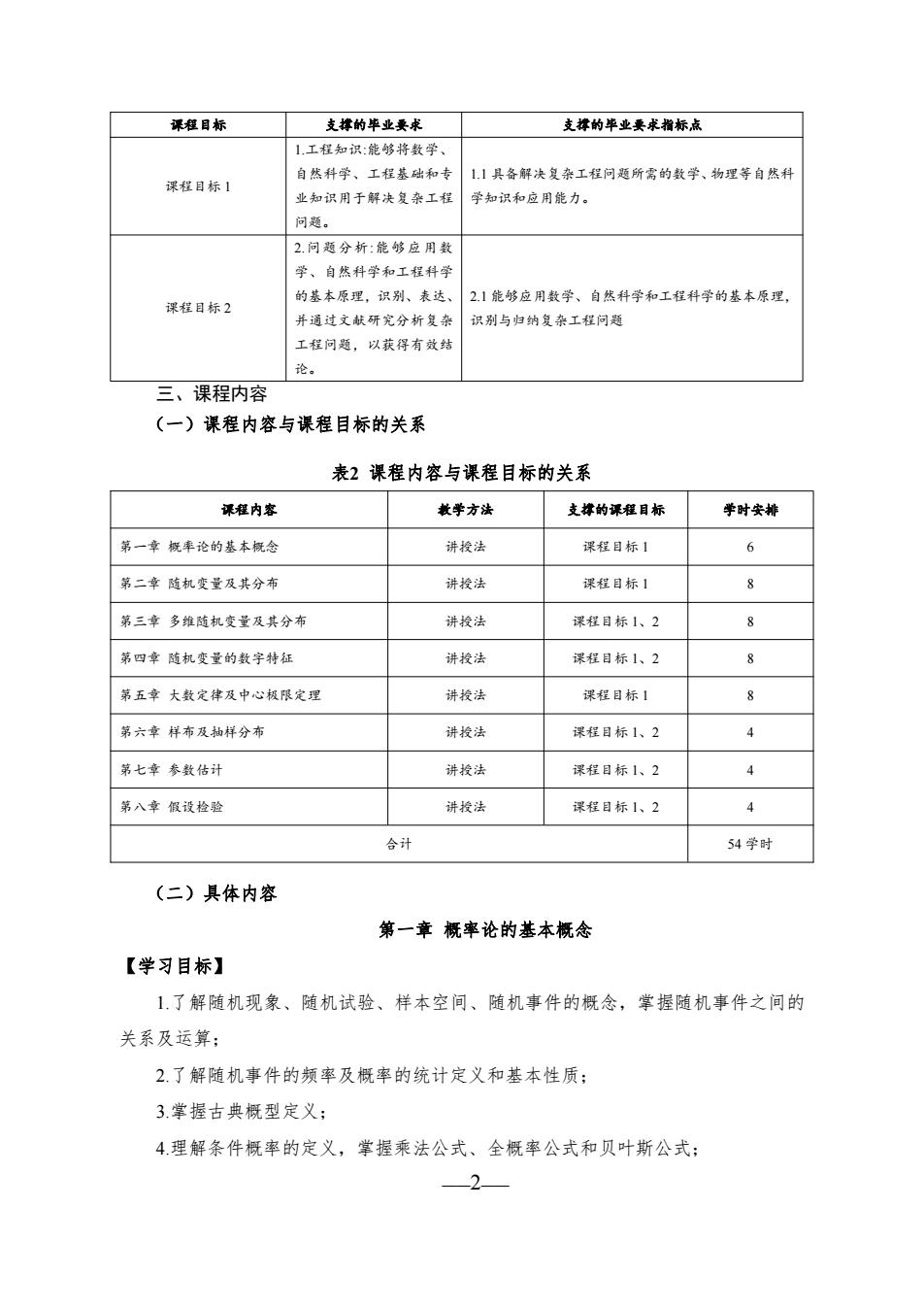
课短目标 支排的毕业要求 支排的单业要求指标底 1工程知识:能够将数学 课程标】 自些科学、工柱基和 1.1具备解决复杂工问题所需的数学、物理等自然科 业知识用于解决复杂工程 学知识和应用能力。 问题。 2问题分析:能够应用数 草、自城科学和工程科 课目标2 的本原理,识别、表达 21能够应用数学、自然科学和工柱科学的基本原理 并通过文就研究分祈复 识别与归纳复杂工程问题 工程问题,以获得有效结 论。 三、课程内容 (一)课程内容与课程目标的关系 表2课程内容与课程目标的关系 课狂内容 教学方法 支撑的课程目标 学时安排 第一章概率论的基本概念 诉投法 课柱日标1 6 第二章随机变量及其分布 讲投法 深日标1 8 第三章多推随机变量及其分布 讲投法 课程目标1、2 8 第四拿随机变童的数字特征 讲投法 课程日标1、2 8 第五章大数定律及中心极限定理 讲投法 谋在目标1 8 第六章样布及抽样分布 讲投法 课程目标1、2 4 第七章泰数估计 游投法 课程目标1、2 4 第八章低说检验 讲授法 课在目标1、2 4 合计 54学时 (二)具体内容 第一章概率论的基本概念 【学习目标】 1了解随机现象、随机试验、样本空间、随机事件的概念,掌握随机事件之间的 关系及运算: 2.了解随机事件的频率及概率的统计定义和基本性质: 3.学握古典概型定义: 4理解条件概率的定义,掌握乘法公式、全概率公式和贝叶斯公式:
——2—— 课程目标 支撑的毕业要求 支撑的毕业要求指标点 课程目标 1 1.工程知识:能够将数学、 自然科学、工程基础和专 业知识用于解决复杂工程 问题。 1.1 具备解决复杂工程问题所需的数学、物理等自然科 学知识和应用能力。 课程目标 2 2.问题分析:能够应用数 学、自然科学和工程科学 的基本原理,识别、表达、 并通过文献研究分析复杂 工程问题,以获得有效结 论。 2.1 能够应用数学、自然科学和工程科学的基本原理, 识别与归纳复杂工程问题 三、课程内容 (一)课程内容与课程目标的关系 表2 课程内容与课程目标的关系 课程内容 教学方法 支撑的课程目标 学时安排 第一章 概率论的基本概念 讲授法 课程目标 1 6 第二章 随机变量及其分布 讲授法 课程目标 1 8 第三章 多维随机变量及其分布 讲授法 课程目标 1、2 8 第四章 随机变量的数字特征 讲授法 课程目标 1、2 8 第五章 大数定律及中心极限定理 讲授法 课程目标 1 8 第六章 样布及抽样分布 讲授法 课程目标 1、2 4 第七章 参数估计 讲授法 课程目标 1、2 4 第八章 假设检验 讲授法 课程目标 1、2 4 合计 54 学时 (二)具体内容 第一章 概率论的基本概念 【学习目标】 1.了解随机现象、随机试验、样本空间、随机事件的概念,掌握随机事件之间的 关系及运算; 2.了解随机事件的频率及概率的统计定义和基本性质; 3.掌握古典概型定义; 4.理解条件概率的定义,掌握乘法公式、全概率公式和贝叶斯公式;

5.理解随机事件独立性的概念,掌握利用事件独立性进行计算。 【学习内容】 1.随机试验 2.随机事件的概率 3.古典概型; 4.条件概率: 5.事件的独立性: 【学习重点】 1随机事件: 2.概率的基本性质及其应用: 3乘法定理、全概率公式与贝叶斯公式: 4.事件的独立性。 【学习难点】 1概率的公理化定义: 2.条件概率概念的建立: 3.全概率公式与贝叶斯公式的应用。 第二章随机变量及其分布 【学习目标】 1理解随机交量的定义,了解用随机变量表示随机事件: 2.了解分布函数的定义及其性质,会利用分布函数计算事件的概率; 3.理解离散型随机变量及其分布列的定义、性质,掌握离散型随机变量的分布律 及分布函数 4.掌握常见的离散型随机变量的分布的概率分布:两点分布、二项分布、泊松分 布: 5理解连续型随机变量及概率密度的定义、性质掌握用密度函数计算概率,掌握 常见的连续型随机变量概率计算:均匀分布、指数分布和正态分布: 6.了解随机变量函数的概念,了解随机变量的简单函数的分布的求法。 【学习内容】 1.随机变量 3
——3—— 5.理解随机事件独立性的概念,掌握利用事件独立性进行计算。 【学习内容】 1.随机试验; 2.随机事件的概率; 3.古典概型; 4.条件概率; 5.事件的独立性; 【学习重点】 1.随机事件; 2.概率的基本性质及其应用; 3.乘法定理、全概率公式与贝叶斯公式; 4.事件的独立性。 【学习难点】 1.概率的公理化定义; 2.条件概率概念的建立; 3.全概率公式与贝叶斯公式的应用。 第二章 随机变量及其分布 【学习目标】 1.理解随机变量的定义,了解用随机变量表示随机事件; 2.了解分布函数的定义及其性质,会利用分布函数计算事件的概率; 3.理解离散型随机变量及其分布列的定义、性质,掌握离散型随机变量的分布律 及分布函数; 4.掌握常见的离散型随机变量的分布的概率分布:两点分布、二项分布、泊松分 布; 5.理解连续型随机变量及概率密度的定义、性质掌握用密度函数计算概率,掌握 常见的连续型随机变量概率计算:均匀分布、指数分布和正态分布; 6.了解随机变量函数的概念,了解随机变量的简单函数的分布的求法。 【学习内容】 1.随机变量;

2离散型随机变量及其概率分布: 3.随机变量的分布函数: 4.连续型随机变量及其概率密度: 5.随机变量函数的分布。 【学习重点】 1随机变量、分布律、密度函数和分布函数的概念: 2.二项分布、均匀分布的概念和性质。 【学习难点】 1二项分布的推导及应用: 2.随机变量函数的概率分布。 第三章多维随机变量及其分布 【学习目标】 L.理解二维随机变量的概念: 2理解二维随机变量的边缘分布以及计算(离散、连续); 3.了解二维随机变量的条件分布,理解随机变量的独立性,掌握判断独立性的方 法。 【学习内容】 1二维随机交量及其分布; 2.条件分布与随机变量的独立性。 【学习重点】 1.由联合分布求概率: 2求边缘分布及条件分布的方法。 【学习难点】 1求离散型随机变量联合分布律的方法: 2.条件密度的导出: 3随机变量函数的分布。 第四章随机变量的数字特征 【学习目标】 1理解随机变量数字特征(数学期望、方差、标准差、协方差,相关系数)的概 A
——4—— 2.离散型随机变量及其概率分布; 3.随机变量的分布函数; 4.连续型随机变量及其概率密度; 5.随机变量函数的分布。 【学习重点】 1.随机变量、分布律、密度函数和分布函数的概念; 2.二项分布、均匀分布的概念和性质。 【学习难点】 1.二项分布的推导及应用; 2.随机变量函数的概率分布。 第三章 多维随机变量及其分布 【学习目标】 1.理解二维随机变量的概念; 2.理解二维随机变量的边缘分布以及计算(离散、连续); 3.了解二维随机变量的条件分布,理解随机变量的独立性,掌握判断独立性的方 法。 【学习内容】 1.二维随机变量及其分布; 2.条件分布与随机变量的独立性。 【学习重点】 1.由联合分布求概率; 2.求边缘分布及条件分布的方法。 【学习难点】 1.求离散型随机变量联合分布律的方法; 2.条件密度的导出; 3.随机变量函数的分布。 第四章 随机变量的数字特征 【学习目标】 1.理解随机变量数字特征(数学期望、方差、标准差、协方差,相关系数)的概

念。 2并会运用数字特征的基本性质计算具体分布的数字特征: 3掌握常用分布的数字特征的概念意义和实际背景,会根据随机变量的概率分布 求其函数的数学期望;会根据随机变量的联合概率分布求其函数的数学期望: 4.掌握随机变量独立性与相关系数的相互关系。 【学习内容】 1随机变量的数学期望与方差及其性质: 2随机变量函数的数学期望与方差: 3.随机变量的协方差与相关系数。 【学习重点】 1一维随机变量函数的数学期望和方差的计算及其性质: 2.二维随机变量的期望、方差、协方差、相关系数的计算,及独立性、相关性的 判断。 【学习难点】 随机变量函数的数学期望与方差。 第五章大数定律及中心极限定律 【学习目标】 1了解大数定律的概念;理解常见的大数定律的内容(如马尔可夫大数定律、切 比雪夫大数定律、贝努利大数定律、辛软大数定律); 2.了解中心极限定理的概念;掌握常见的中心极限定理(隶莫弗一拉普拉斯中心 极限定理、林德贝格一勒维中心极限定理)及其应用。 【学习内容】 1大数定律的概念: 2.中心极限定律的概念及应用。 【学习重点】 常见的大数定律与中心极限定理及其筒单应用。 【学习难点】 常见的中心极限定理及其应用。 第六章样本及抽样分布
——5—— 念。 2.并会运用数字特征的基本性质计算具体分布的数字特征; 3.掌握常用分布的数字特征的概念意义和实际背景,会根据随机变量的概率分布 求其函数的数学期望;会根据随机变量的联合概率分布求其函数的数学期望; 4.掌握随机变量独立性与相关系数的相互关系。 【学习内容】 1.随机变量的数学期望与方差及其性质; 2.随机变量函数的数学期望与方差; 3.随机变量的协方差与相关系数。 【学习重点】 1.一维随机变量函数的数学期望和方差的计算及其性质; 2.二维随机变量的期望、方差、协方差、相关系数的计算,及独立性、相关性的 判断。 【学习难点】 随机变量函数的数学期望与方差。 第五章 大数定律及中心极限定律 【学习目标】 1.了解大数定律的概念;理解常见的大数定律的内容(如马尔可夫大数定律、切 比雪夫大数定律、贝努利大数定律、辛钦大数定律); 2.了解中心极限定理的概念;掌握常见的中心极限定理(隶莫弗-拉普拉斯中心 极限定理、林德贝格-勒维中心极限定理)及其应用。 【学习内容】 1.大数定律的概念; 2.中心极限定律的概念及应用。 【学习重点】 常见的大数定律与中心极限定理及其简单应用。 【学习难点】 常见的中心极限定理及其应用。 第六章 样本及抽样分布

【学习目标】 1掌握随机样本、样本值、独立观察值的概念: 2使用直方图、箱线图解决实际应用习题: 3.掌握x分布、t分布和F分布的定义及性质,掌握其分位数的概念并会查表计 算。 【学习内容】 1.随机样本相关概念: 2.箱线图、直方图的使用; 3.X2分布、t分布和下分布的定义及性质。 【学习重点】 X分布、t分布和F分布的定义及性质。 【学习难点】 X分布、t分布和F分布的定义及性质。 第七章参数估计 【学习目标】 1理解参数的点估计、估计量与估计值的概念: 2.掌握矩估计法和极大似然估计法; 3了解估计量的评价标准(无偏性、有效性、一致性)的概念,并会验证估计量 的无偏性: 4了解区间估计的概念: 5掌握单个正态总体的均值和方差的置信区间: 6.掌握两个正态总体的均值差和方差比的置信区间。 【学习内容】 1.点估计: 2.估计量的评选标准 3.区间估计: 4.正态总体均值与方差的区问估计: 6
——6—— 【学习目标】 1.掌握随机样本、样本值、独立观察值的概念; 2.使用直方图、箱线图解决实际应用习题; 3.掌握 2分布、t 分布和 F 分布的定义及性质,掌握其分位数的概念并会查表计 算。 【学习内容】 1.随机样本相关概念; 2.箱线图、直方图的使用; 3. 2分布、t 分布和 F 分布的定义及性质。 【学习重点】 2分布、t 分布和 F 分布的定义及性质。 【学习难点】 2分布、t 分布和 F 分布的定义及性质。 第七章 参数估计 【学习目标】 1.理解参数的点估计、估计量与估计值的概念; 2.掌握矩估计法和极大似然估计法; 3.了解估计量的评价标准(无偏性、有效性、一致性)的概念,并会验证估计量 的无偏性; 4.了解区间估计的概念; 5.掌握单个正态总体的均值和方差的置信区间; 6.掌握两个正态总体的均值差和方差比的置信区间。 【学习内容】 1.点估计; 2.估计量的评选标准; 3.区间估计; 4.正态总体均值与方差的区间估计;

5.(01)分布参数的区问估计: 6.单侧置信区间。 【学习重点】 矩估计法、校大似然估计法、区间估计。 【学习难点】 估计量的一致性。 第八章假设检验 【学习目标】 1理解显著性检验的基本思想,掌握假设检验的基本步骤,知道假设检验可能产 生的两类错误: 2熟练掌握单个正态总体的均值和方差的假设检验,了解两个正态总体的均值和 方差的假设检验: 3.知道总体分布假设的检验法。 【学习内容】 1正态总体均值、方差的假设检验: 2执行区问与假设检验之间的关系: 3.分布拟合实验。 【学习重点】 单个正态总体的均值与方差的假设检验。 【学习难点】 假设检验的原理与方法。 四、教学方法 讲授法。 五、课程考核 考核方式:平时考核+期末考试。 本课程为考试课,考试由平时考核及期末考试两部分构成,平时考核由课堂考勤 (a1)、平时作业(am)、阶段性测试(a)三部分构成,所占的权重分别为a1=10%、 am=15%、s=5%。期末考试为闭卷考试,卷面总分100分,占课程考核的权重a4=70%。 7
——7—— 5.(0-1)分布参数的区间估计; 6.单侧置信区间。 【学习重点】 矩估计法、极大似然估计法、区间估计。 【学习难点】 估计量的一致性。 第八章 假设检验 【学习目标】 1.理解显著性检验的基本思想,掌握假设检验的基本步骤,知道假设检验可能产 生的两类错误; 2.熟练掌握单个正态总体的均值和方差的假设检验,了解两个正态总体的均值和 方差的假设检验; 3.知道总体分布假设的检验法。 【学习内容】 1.正态总体均值、方差的假设检验; 2.执行区间与假设检验之间的关系; 3.分布拟合实验。 【学习重点】 单个正态总体的均值与方差的假设检验。 【学习难点】 假设检验的原理与方法。 四、教学方法 讲授法。 五、课程考核 考核方式:平时考核+期末考试。 本课程为考试课,考试由平时考核及期末考试两部分构成,平时考核由课堂考勤 (a1)、平时作业(a2)、阶段性测试(a3)三部分构成,所占的权重分别为 a1=10%﹑ a2 =15%、a3 =5%。期末考试为闭卷考试,卷面总分 100 分,占课程考核的权重 a4=70%

课程总成绩(100%)=课堂考勒(a1)+平时作业(am)+阶段性测试(a3)+期 末成绩(a4) 表3各考核环节建议值及考核细则 课程成绩枸成及比例 考核方式 目标位 考核细则 对应谋程目标 教师随堂点名,年学点名三次以 课堂考勤a 课堂考勤 100 上,根据学生出勤清况作为课空 保程日标1、2 勤成绩。 平时作业a 课程作业 100 每次作业单独评分,取平均分作为 平时作业成特。 课柱日标1、2 阶役性测试a出 阶性测试 100 织3次随堂测险,年次测单独 评分,取平均分作为课堂测验成绩 课程日标1、2 卷面成墙100分。题型以选择题 期末考试a 期末考试 100 课柱日标1、2 填空题、判断题、计算题等为主, 六、课程评价 课程目标达成度评价包括课程分目标达成度评价和课程总目标达成度评价,具体 计算方法如下: 相关评价方式加权平均得分 课程分目标达成度= 相关评价方式目标加权总分 课程总目标达成度=课程所有分目标达成度加权值之和 课程目标评价内容及符号意义说明:4为平时成绩对应课程目标1的得分,B,为 期末考试成绩对应课程目标1的得分;O4:为平时成绩对应课程目标1的目标分值, OB,为期末考试对应课程目标1的目标分值;片为课程目标1在总目标达成度中的权重 值:S为课程总目标的达成度,S为课程目标i的达成度。 表4课程考核成绩对课程目标达成情况评价 课柱日标误程日标权重 评价方式 目标分值 实际平均分 日标达成评价值 课堂考勤 0A1-=40 平时作业 04,=40 A1 课程目标】 0.4 阶段性测试 0.=40 50光院导8 期末成 0B1=40 B 课堂考勒 0A.=60 A3. 平时作业 042.=60 课程目标2 0.6 0.=60 -0o8 期末成绩 OB2-=60
——8—— 课程总成绩(100%)=课堂考勤(a1)+ 平时作业(a2)+阶段性测试(a3)+期 末成绩(a4) 表 3 各考核环节建议值及考核细则 课程成绩构成及比例 考核方式 目标值 考核细则 对应课程目标 课堂考勤 a1 课堂考勤 100 教师随堂点名,每学期点名三次以 上,根据学生出勤情况作为课堂考 勤成绩。 课程目标 1、2 平时作业 a2 课程作业 100 每次作业单独评分,取平均分作为 平时作业成绩。 课程目标 1、2 阶段性测试 a3 阶段性测试 100 组织 3 次随堂测验,每次测验单独 评分,取平均分作为课堂测验成绩。 课程目标 1、2 期末考试 a4 期末考试 100 卷面成绩 100 分。题型以选择题、 填空题、判断题、计算题等为主。 课程目标 1、2 六、课程评价 课程目标达成度评价包括课程分目标达成度评价和课程总目标达成度评价,具体 计算方法如下: 相关评价方式目标加权总分 相关评价方式加权平均得分 课程分目标达成度 课程总目标达成度=课程所有分目标达成度加权值之和 课程目标评价内容及符号意义说明:Ai 为平时成绩对应课程目标 i 的得分,Bi 为 期末考试成绩对应课程目标 i 的得分;OAi 为平时成绩对应课程目标 i 的目标分值, OBi为期末考试对应课程目标 i 的目标分值;γi为课程目标 i 在总目标达成度中的权重 值;S 为课程总目标的达成度,Si为课程目标 i 的达成度。 表 4 课程考核成绩对课程目标达成情况评价 课程目标 课程目标权重 评价方式 目标分值 实际平均分 目标达成评价值 课程目标 1 0.4 课堂考勤 OA1-1=40 A1-1 1 1 1 2 1 2 3 1 3 4 1 1 1 1 1 2 1 2 3 1 3 4 1 a A a A a A a B S a OA a OA a OA a OB 平时作业 OA1-2=40 A1-2 阶段性测试 OA1-3=40 A1-3 期末成绩 OB1=40 B1 课程目标 2 0.6 课堂考勤 OA2-1=60 A2-1 1 2 1 2 2 2 3 2 3 4 2 2 1 2 1 2 2 2 3 2 3 4 2 a A a A a A a B S a OA a OA a OA a OB 平时作业 OA2-2=60 A2-2 阶段性测试 OA2-3=60 A2-3 期末成绩 OB2=60 B2

课程目标1权 果程总目标 重不 保程总成绩 100 达成度 s=2 注:1.目标分值为课程目标对应评价方式的满分,同一评价方式目标分值之和为100。 2实际平均分为参与评价的学生在该评价方式的平均分。 七、课程资源 (一)建议选用散材 [茆诗松,周纪芗,张日权.概率论与数理统计(第四版)M北京:中国统计出版 社,2020. (二)主要参考书目 [山盛骤,谢式千,潘承毅.概率论与数理统计(第四版)M.北京:高等教育出版社。 2008 [2]盛骤,谢式千,潘承毅.概率论与数理统计习题全解指南(第四版)M北京:高等 教育出版社,2008. (三)其它课程资源 1.浙江大学概率论与数理统计慕课 https://www.icourse163.org/course/ZJU-232005?from=searchPage&out Vendor=zw_moo 2.电子科技大学概率论与数理统计幕课 https://www.icourse163.org/course/UESTC-1001590004?from=searchPage&out Vendor= zw_mooc_pcssjg 执笔人:袁亮 课程负责人:袁亮 审核人(系/散研室主任):张宗领 审定人(主管教学副院长副主任):袁晓辉 2023年6月 _9
——9—— 课程目标 i 权 重和 1.0 2 1 i i 课程总成绩 100 课程总目标 达成度 2 i 1 S iSi 注:1.目标分值为课程目标对应评价方式的满分,同一评价方式目标分值之和为 100。 2.实际平均分为参与评价的学生在该评价方式的平均分。 七、课程资源 (一)建议选用教材 [1]茆诗松, 周纪芗, 张日权. 概率论与数理统计(第四版)[M]. 北京: 中国统计出版 社,2020. (二)主要参考书目 [1]盛骤, 谢式千,潘承毅. 概率论与数理统计(第四版)[M]. 北京: 高等教育出版社, 2008. [2]盛骤,谢式千,潘承毅. 概率论与数理统计习题全解指南(第四版)[M]. 北京: 高等 教育出版社,2008. (三)其它课程资源 1.浙江大学概率论与数理统计慕课 https://www.icourse163.org/course/ZJU-232005?from=searchPage&outVendor=zw_moo c_pcssjg 2.电子科技大学概率论与数理统计慕课 https://www.icourse163.org/course/UESTC-1001590004?from=searchPage&outVendor= zw_mooc_pcssjg 执笔人:袁亮 课程负责人:袁亮 审核人(系/教研室主任):张宗领 审定人(主管教学副院长/副主任):袁晓辉 2023 年 6 月