
试验设计与分析 响应面设计与分析 第六章 响应面试验设计与分析
试验设计与分析 响应面设计与分析

试验设计与分析 响应面设计与分析 1.什么是响应面法 >响应面设计方法(Response Surface Methodology,RSMW是利用合理的试验设 计方法并通过实验得到一定数据,采用多元二次回归方程来拟合因素与响应 值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变 量非线性问题及可视化的一种统计方法。 可分为: >中心复合试验设计(Central Composite Design,CCD); >Box-Behnken试验设计(BB)。 在响应分析中,观察值y可以表述为: y=f(x1,x2…,x1)+8 其中xx,是自变量,2…,的函数,是误差项。 在响应面分析中,首先要得到回归方程,然后通过对自变量x,x2, 的合理取值,求得使少=f(x,x2,…,x,)最优的值,这就是响应面设计 试验的目的
试验设计与分析 响应面设计与分析 Ø响应面设计方法(Response Surface Methodology,RSM)是利用合理的试验设 计方法并通过实验得到一定数据,采用多元二次回归方程来拟合因素与响应 值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变 量非线性问题及可视化的一种统计方法。 可分为: Ø中心复合试验设计(Central Composite Design,CCD); ØBox-Behnken试验设计(BB)。 在响应分析中,观察值y可以表述为: 其中 是自变量 的函数,ε是误差项。 在响应面分析中,首先要得到回归方程,然后通过对自变量 的合理取值,求得使 最优的值,这就是响应面设计 试验的目的。 ( , , , ) l y f x x x 1 2 f(x1,x2,,xl ) l x ,x ,,x 1 2 l x ,x ,,x 1 2 ( , , , )l y f x x x 1 2 ˆ
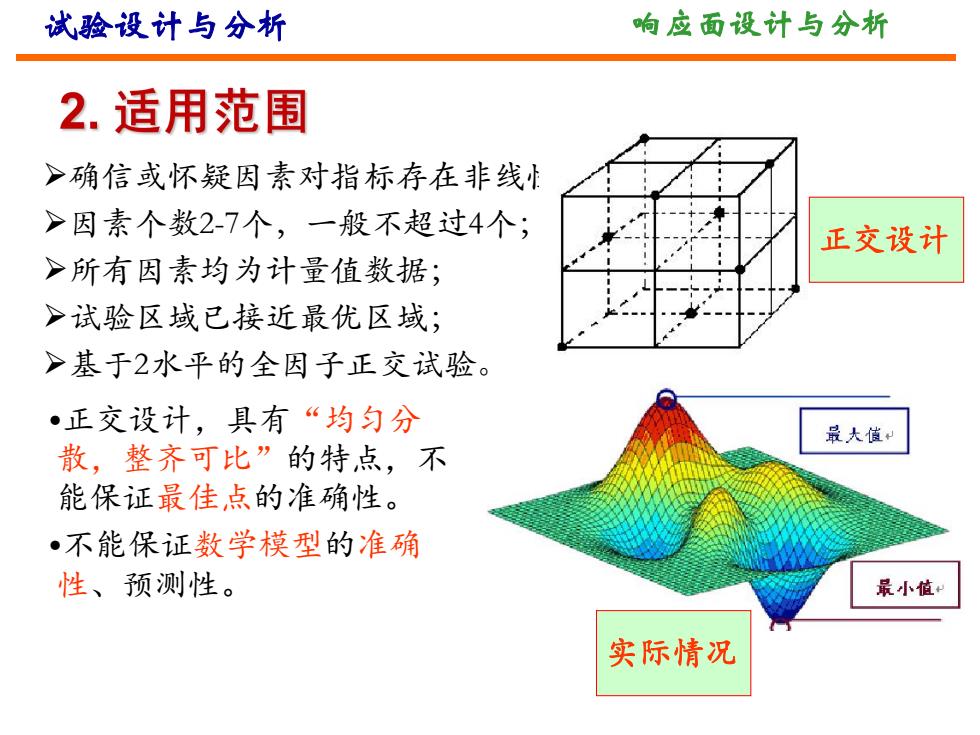
试验设计与分析 响应面设计与分析 2.适用范围 >确信或怀疑因素对指标存在非线 >因素个数2-7个,一般不超过4个; 正交设计 >所有因素均为计量值数据; >试验区域已接近最优区域; >基于2水平的全因子正交试验。 •正交设计,具有“均匀分 最大值 散,整齐可比”的特点,不 能保证最佳点的准确性。 •不能保证数学模型的准确 性、预测性。 最小值 实际情况
试验设计与分析 响应面设计与分析 Ø确信或怀疑因素对指标存在非线性影响; Ø因素个数2-7个,一般不超过4个; Ø所有因素均为计量值数据; Ø试验区域已接近最优区域; Ø基于2水平的全因子正交试验。 正交设计 实际情况 •正交设计,具有“均匀分 散,整齐可比”的特点,不 能保证最佳点的准确性。 •不能保证数学模型的准确 性、预测性

试验设计与分析 响应面设计与分析 3.一般步骤 1.确定因素及水平,注意水平数为2,因素数一 般不超过4个,因素均为计量值数据; 2.创建“中心复合”或“Box-Behnken”设计; 3.确定试验运行顺序(Display Design); 4.进行试验并收集数据; 5.分析试验数据; 6.优化因素的设置水平
试验设计与分析 响应面设计与分析 1. 确定因素及水平,注意水平数为2,因素数一 般不超过4个,因素均为计量值数据; 2. 创建“中心复合”或“Box-Behnken ”设计; 3. 确定试验运行顺序(Display Design); 4. 进行试验并收集数据; 5. 分析试验数据; 6. 优化因素的设置水平

试验设计与分析 响应面设计与分析 4.中心复合试验设计 ●中心复合设计(星点设计, 最大值 Central Composite Designs,CCD) 最小值 是应用得最为广泛的试验设计方法。 ●理解的关键CCD设计布点中心 中央点 点:点数要足够多,保证中央点 ·析因点 即最佳点的准确性。 ★轴点 析因点:构建多元回归模型,一个 立方体的2K顶,点,连续性。 图1CCD组成部分示意图 轴点:延展性,带有参数的2k个 轴向点,不需要准确性
试验设计与分析 响应面设计与分析 l中心复合设计(星点设计, Central Composite Designs,CCD) 是应用得最为广泛的试验设计方法。 l 理解的关键 CCD设计布点 中心 点:点数要足够多,保证中央点 即最佳点的准确性。 析因点:构建多元回归模型,一个 立方体的2 K顶点,连续性。 轴点:延展性,带有参数α的2k个 轴向点,不需要准确性

试验设计与分析 响应面设计与分析 α的选取 在的选取上可以有多种出发,点,旋转性是个很有意义的考 虑。在k个因素的情况下,应取 α=2k/4 当k=2,0=1.414;当k=3,0=1.682; 当k=4,=2.000;当k=5,0=2.378 实例:星点设计-效应面法优选灯盏花乙素超声提取
试验设计与分析 响应面设计与分析 α的选取 在α的选取上可以有多种出发点,旋转性是个很有意义的考 虑。在k个因素的情况下,应取 α=2 k/4 当k=2, α=1.414;当k=3,α =1.682; 当k=4, α=2.000;当k=5,α =2.378 实例:星点设计-效应面法优选灯盏花乙素超声提取
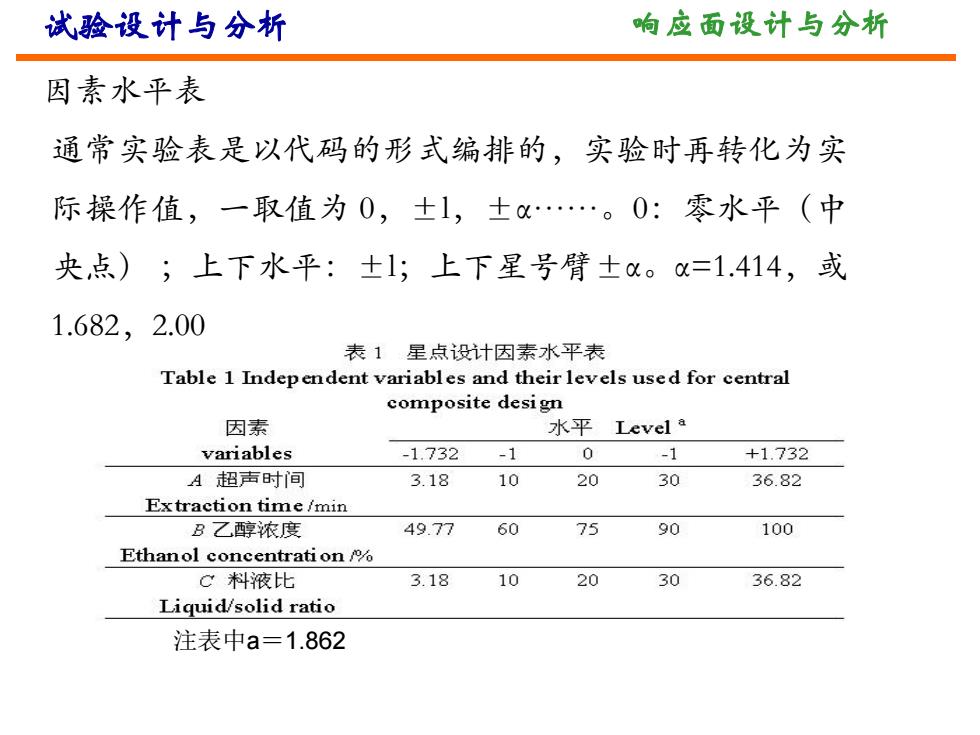
试验设计与分析 响应面设计与分析 因素水平表 通常实验表是以代码的形式编排的,实验时再转化为实 际操作值,一取值为0,±1,士…。0:零水平(中 央点);上下水平:±1;上下星号臂±。=1.414,或 1.682,2.00 表1星点设计因素水平表 Table 1 Independent variables and their levels used for central composite design 因素 水平Levela variables -1.732 -1 0 -1 +1.732 A超声时间 3.18 10 20 30 36.82 Extraction time/min B乙醇浓度 49.77 60 75 90 100 Ethanol concentration C料液比 3.18 10 20 30 36.82 Liquid/solid ratio 注表中a=1.862
试验设计与分析 响应面设计与分析 因素水平表 通常实验表是以代码的形式编排的,实验时再转化为实 际操作值,一取值为 0,±l,±α……。0:零水平(中 央点) ;上下水平:±l;上下星号臂±α。α=1.414,或 1.682,2.00 注表中a=1.862
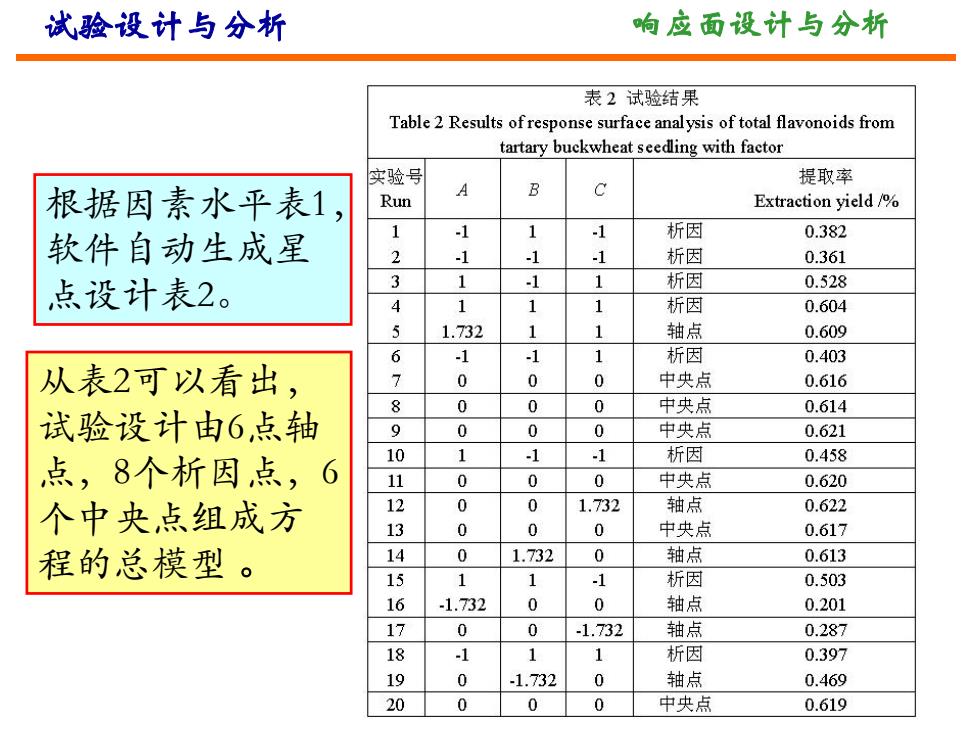
试验设计与分析 响应面设计与分析 表2试验结果 Table 2 Results of response surface analysis of total flavonoids from tartary buckwheat seedling with factor 实验号 提取率 根据因素水平表1 A C Run Extraction yield% 1 软件自动生成星 -1 1 -1 析因 0.382 2 -1 -1 -1 析因 0.361 点设计表2。 1 -1 析因 0.528 析因 0.604 1.732 1 轴点 0.609 1 析因 0.403 从表2可以看出, 0 0 0 中央点 0.616 8 0 0 0 中央点 0.614 试验设计由6,点轴 9 0 0 0 中央点 0.621 10 1 点,8个析因点,6 -1 1 析因 0.458 11 0 0 0 中央点 0.620 个中央点组成方 12 0 1.732 轴点 0.622 13 0 0 0 中央点 0.617 程的总模型。 14 0 1.732 0 轴点 0.613 15 1 1 -1 析因 0.503 16 1.732 0 0 轴点 0.201 17 0 0 -1.732 轴点 0.287 18 2 1 析因 0.397 19 0 -1.732 0 轴点 0.469 20 0 0 0 中央点 0.619
试验设计与分析 响应面设计与分析 根据因素水平表1, 软件自动生成星 点设计表2。 从表2可以看出, 试验设计由6点轴 点,8个析因点,6 个中央点组成方 程的总模型

试验设计与分析 响应面设计与分析 •对表2中的实验数据进行多元线性回归和二项式拟合,获得灯盏花乙 素提取的数学模型如下:E=-0.85615+0.029944A+0.018569B+0.026062C +8.83333×105AB+1.42500×104AC +3.33333×106BC-7.59177×104A2 -1.23708×104B2-5.84168×104C2 表3回归方程的方差分析表 Table 3 Analysis of variance for response surface quadratic mode 方差来源自由度 平方和 均方差 F值 模型显著 Source df Sum of squares Mean Square FValue Prob>F 总模型 9 0.30 0.033 11.49 0.05 1 0.046 0.046 16.04 0.05 AC 1 1.625×10 0.57 0.57 >0.05 BC 1 2.000X10 6.994X10 6.994X10 >0.05 A2 1 0.083 29.05 29.05 0.05 c2 1 0.049 17.20 17.20 <0.05 残差 5 0.029 2.860×10 总变异 19 0.32 *6s954.78,6195广10.15
试验设计与分析 响应面设计与分析 模型显著 交互顶 因素显著性 显著性 •对表2中的实验数据进行多元线性回归和二项式拟合,获得灯盏花乙 素提取的数学模型如下: -5 -4 -6 -4 2 -4 2 -4 2 =-0.85615+0.029944 +0.018569 +0.026062 +8.83333 10 +1.42500 10 +3.33333 10 -7.59177 10 -1.23708 10 -5.84168 10 E A B C AB AC BC A B C

试验设计与分析 响应面设计与分析 内部的误差估计量: >模型的F>F0.o19,),说明回归方程在0.01的水平显著,表 明试验设计可靠 >模型相关系数=0.9549,进一步说明模型具有较好的可信 度。 >失拟度:不显著,说明实验点均能用模型描述。 各因素影响显著性比较: >根据方差分析(离散分析,表3),P值代表了因素的显著性水平,比 较p值,影响的显著性排序,提取时间(A,p料液比(B, ×0.01)>乙醇浓度(C,p方程的交互项的AB、AC和BC均p>0.05表明,交互顶对灯盏花乙素得 率的影响不显著,表明三个因素无交互作用
试验设计与分析 响应面设计与分析 内部的误差估计量: Ø模型的F>F0.01(9,5),说明回归方程在 0.01的水平显著,表 明试验设计可靠. Ø模型相关系数r=0.9549,进一步说明模型具有较好的可信 度。 Ø失拟度:不显著,说明实验点均能用模型描述。 各因素影响显著性比较: Ø根据方差分析(离散分析,表3),p值代表了因素的显著性水平,比 较p值,影响的显著性排序,提取时间( A , p 料液比(B, p乙醇浓度 (C , p0.05表明,交互顶对灯盏花乙素得 率的影响不显著,表明三个因素无交互作用