
粒子图像测速技术 课程讲义 授课人: 杜海 单位:大连理工大学建设工程学部 编制日期:2016年4月5日
粒 子 图 像 测 速 技 术 课 程 讲 义 授课人: 杜 海 单 位:大连理工大学 建设工程学部 编制日期: 2016 年 4 月 5 日

第一章:粒子图像测试技术与摄影测量法 1.1概述 粒子图像测速技术(Particle Image Velocimetry,.PIV)是在流动显示基 础上发展起来的一种散斑图像测速技术。该技术充分利用了像面上所“冻结”的 流场信息来剖析流体运动,具有非接触式测量的特点。PIV技术作为一种具有代 表性的运动追踪测量技术在各个应用研究领域中也显示出其独特的魅力与重要 价值,如在医学研究领域中血液流动测试、在工程领域中的管道测量、在环境研 究领域的搅拌器流动测试、水产养殖领域的人工渔礁周围流场测试、航空领域中 的飞行器风洞测试、汽车研究领域中的车体结构流动测试等等。目前PIV技术作 为一种流体测量技术的价值已在科研与工业中得到了充分的验证,应用举例见图 1-1。 (a)飞行器设计 (b)管道研究 (c)船舶研制 图1-1PIV在给个行业中的应用 在流体测量技术的发展中看粒子图像测速的技术特点 在过去的几十年里,为了满足人们研究流动的物理机理及动力学特性的需要, 流体测量技术取得了很多进展。以流速测量为例,传统的皮托管测速成本低、操 作简单,但它的动态性能差,对流场扰动大,精度不高。热线热膜流速计(WAF) 结合了现代迅猛发展的电子技术,测量精度和频响都大大提高了,但如果流场范 围较小,与探头大小可比时,测量的空间分辨率受到限制,且此时对流场的影响 很大。相比之下,激光多普勒测速仪(LDV)在测量较小的流场时显示出它的非 接触式测量的优点,具有极好的时间分辨率和空间分辨力,可做三维测速,已经 成为流速测量的标准技术并得到了广泛应用。相位多普勒测速仪(PDA或PDAP) 不仅能像LDⅣ那样给出粒子的速度,而且可以给出粒子的粒径,在两相流动的测
第一章:粒子图像测试技术与摄影测量法 1.1 概 述 粒子图像测速技术(Particle Image Velocimetry, PIV)是在流动显示基 础上发展起来的一种散斑图像测速技术。该技术充分利用了像面上所“冻结”的 流场信息来剖析流体运动,具有非接触式测量的特点。PIV 技术作为一种具有代 表性的运动追踪测量技术在各个应用研究领域中也显示出其独特的魅力与重要 价值,如在医学研究领域中血液流动测试、在工程领域中的管道测量、在环境研 究领域的搅拌器流动测试、水产养殖领域的人工渔礁周围流场测试、航空领域中 的飞行器风洞测试、汽车研究领域中的车体结构流动测试等等。目前 PIV 技术作 为一种流体测量技术的价值已在科研与工业中得到了充分的验证,应用举例见图 1-1。 (a) 飞行器设计 (b) 管道研究 (c) 船舶研制 图 1-1 PIV 在给个行业中的应用 在流体测量技术的发展中看粒子图像测速的技术特点 在过去的几十年里,为了满足人们研究流动的物理机理及动力学特性的需要, 流体测量技术取得了很多进展。以流速测量为例,传统的皮托管测速成本低、操 作简单,但它的动态性能差,对流场扰动大,精度不高。热线热膜流速计(HWAF) 结合了现代迅猛发展的电子技术,测量精度和频响都大大提高了,但如果流场范 围较小,与探头大小可比时,测量的空间分辨率受到限制,且此时对流场的影响 很大。相比之下,激光多普勒测速仪(LDV)在测量较小的流场时显示出它的非 接触式测量的优点,具有极好的时间分辨率和空间分辨力,可做三维测速,已经 成为流速测量的标准技术并得到了广泛应用。相位多普勒测速仪(PDA 或 PDAP) 不仅能像 LDV 那样给出粒子的速度,而且可以给出粒子的粒径,在两相流动的测

量中得到了广泛的应用。然而,它和LDV以及热线流速仪一样,都只是孤立点测 量技术。在对流动测量过程中,这些方法的使用或多或少地干扰了流场的自由运 动,而且很难获得细致的流动图像,难以满足瞬态流场测试的需要。流动显示技 术对于提供瞬态流动图案无疑是非常有效的,但在定量上遇到了很大的困难,精 度方面也很难满足测试要求。 随着科学技术的发展,在流体研究需求的刺激下,流动显示技术结合光学、 图像处理及计算机技术,将流动显示所获得的定性图像推向定量化,PIV技术应 运而生。该技术综合了孤立点测量技术和显示测量技术的优点,克服了两种测量 技术的弱点而成,可通过流场图像的分析获得流动结构,因此既具备单点测量技 术的精度和分辨率,又能获得流动显示的瞬态信息和整体结构。PIV技术的这个 特点使得该技术具有获得小尺度结构矢量图的能力,这对于既拥有很宽范围的运 动尺度,又要求具有能分析足够小尺度的空间分辩率的湍流研究无疑是非常重要 的。另外,PV的技术特点也使得它可以满足一些稳定流动的测试需要。所谓稳 定流动指的是速度脉动与平均速度相比很小的流动。实际流动中存在着许多特殊 情况,比如狭窄流场,其流动本身是稳定的,但流场狭小,LDⅣ的分光束难以相 交成可测状态,而FA又会破坏流场的状态,此时粒子图像测速技术便能派上 用场了。 1.2PIV测速原理及系统结构 PIV技术来源于流动显示技术,主要通过图像分析技术追踪散布在流场中小 颗粒,并用这些颗粒的运动来表征流体的运动,其具体操作过程为:首先在流场 中布撒示踪粒子,使用532m的激光或其他光源照亮所测流场区域,通过连续两 次或多次曝光,粒子的图像被记录在底片上或成像在CCD面上:然后采用自相关 法、互相关法以及颗粒跟踪等方法处理粒子图像,计算出流场中各点的流速矢量: 最后根据需求,反演出其他运动参量(包括流场速度矢量图、速度分量图、流线 图等)。从本质上来讲,粒子图像测速测出的是流场中粒子的速度,是利用布撒 在流体中的跟随性较好的示踪粒子来代表粒子所在位置的流场速度。 图1-2PIV测速原理
量中得到了广泛的应用。然而,它和 LDV 以及热线流速仪一样,都只是孤立点测 量技术。在对流动测量过程中,这些方法的使用或多或少地干扰了流场的自由运 动,而且很难获得细致的流动图像,难以满足瞬态流场测试的需要。流动显示技 术对于提供瞬态流动图案无疑是非常有效的,但在定量上遇到了很大的困难,精 度方面也很难满足测试要求。 随着科学技术的发展,在流体研究需求的刺激下,流动显示技术结合光学、 图像处理及计算机技术,将流动显示所获得的定性图像推向定量化,PIV 技术应 运而生。该技术综合了孤立点测量技术和显示测量技术的优点,克服了两种测量 技术的弱点而成,可通过流场图像的分析获得流动结构,因此既具备单点测量技 术的精度和分辨率,又能获得流动显示的瞬态信息和整体结构。PIV 技术的这个 特点使得该技术具有获得小尺度结构矢量图的能力,这对于既拥有很宽范围的运 动尺度,又要求具有能分析足够小尺度的空间分辩率的湍流研究无疑是非常重要 的。另外,PIV 的技术特点也使得它可以满足一些稳定流动的测试需要。所谓稳 定流动指的是速度脉动与平均速度相比很小的流动。实际流动中存在着许多特殊 情况,比如狭窄流场,其流动本身是稳定的,但流场狭小,LDV 的分光束难以相 交成可测状态,而 HWFA 又会破坏流场的状态,此时粒子图像测速技术便能派上 用场了。 1.2 PIV 测速原理及系统结构 PIV技术来源于流动显示技术,主要通过图像分析技术追踪散布在流场中小 颗粒,并用这些颗粒的运动来表征流体的运动,其具体操作过程为:首先在流场 中布撒示踪粒子,使用532nm的激光或其他光源照亮所测流场区域,通过连续两 次或多次曝光,粒子的图像被记录在底片上或成像在CCD面上;然后采用自相关 法、互相关法以及颗粒跟踪等方法处理粒子图像,计算出流场中各点的流速矢量; 最后根据需求,反演出其他运动参量(包括流场速度矢量图、速度分量图、流线 图等)。从本质上来讲,粒子图像测速测出的是流场中粒子的速度,是利用布撒 在流体中的跟随性较好的示踪粒子来代表粒子所在位置的流场速度。 图1-2 PIV测速原理

如图1-2所示,测量粒子经过△1时间的移动,其位置从(x0),),())变化 到(x(+),+),+),当时间间隔△M足够小,以至于小到与受精度约 束的拉格朗日速度场的泰勒微尺度可以比较的程度。此时,粒子的速度可以用位 移与时间间隔的比值来近似,如式(1-1)所示。 =网、+-0 d =m0、+4-地 (1-1) d At Ar 根据式(1-1)可知只要在图像分析过程中获得粒子的位移信息,然后配合摄 像机的定标参数,便可以得到该粒子的空间位移信息,另外由于在一次实验中△“ 是固定的,所以该粒子在笛卡尔坐标系中的速度矢量可以计算得到。当获知足够 多粒子的位移情况即可重建整个流场的速度分布。 PIV技术按照示踪粒子的浓度大小可分为粒子跟踪测速技术(Particle Tracking Velocimetry,,PTV)、粒子图像测速技术(这里指使用区域匹配方法的 PIV)和激光散斑测速技术(Laser Speckle Velocimetry.,LSV)。当粒子浓度极 低时,可以通过识别、跟踪单个粒子的运动,从所采集的粒子图像中直接测得单 个粒子的位移,这种低粒子密度模式的图像测速方法即为PTV技术:当流场中粒 子浓度很高时,以至于粒子在成像系统像平面上形成激光散斑图案(散斑已经掩 盖了真实的粒子图像),这种极高粒子密度模式的图像测速方法即LSV技术:PIV 技术则是指粒子浓度较高的成像模式,但尚未在成像系统像面上形成散斑图案, 仍然是真实的粒子图像的图像测量方法,由于此时粒子的识别工作较为困难,只 能获得一小块兴趣区域内多个粒子位移的统计平均值。LSV技术由于其高粒子浓 度对流场干扰较大,目前己很少采用:PTV技术由于粒子稀疏,可以通过跟踪单 个粒子的运动轨迹测得速度,比PIV测速方法更容易从二维推广到三维,但PTV 技术所提取的流场速度信息较少,这也限制了它在流场细微结构研究中的应用。 根据粒子图像测速技术原理,PIV系统一般包含四个主要部分:示踪粒子、光 学照明部分、图像采集部分以及图像处理部分。如图1-3所示
如图1-2所示,测量粒子经过 t 时间的移动,其位置从( xt() , yt() , zt() )变化 到( x t t ( ) , y t t ( ) , z t t ( ) ),当时间间隔 t 足够小,以至于小到与受精度约 束的拉格朗日速度场的泰勒微尺度可以比较的程度。此时,粒子的速度可以用位 移与时间间隔的比值来近似,如式(1-1)所示。 x y z 0 0 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) lim lim lim dt dt dt dx t x t t x t v dt t dy t y t t y t v dt t dz t z t t z t v dt t (1-1) 根据式(1-1)可知只要在图像分析过程中获得粒子的位移信息,然后配合摄 像机的定标参数,便可以得到该粒子的空间位移信息,另外由于在一次实验中 t 是固定的,所以该粒子在笛卡尔坐标系中的速度矢量可以计算得到。当获知足够 多粒子的位移情况即可重建整个流场的速度分布。 PIV 技术按照示踪粒子的浓度大小可分为粒子跟踪测速技术(Particle Tracking Velocimetry, PTV)、粒子图像测速技术(这里指使用区域匹配方法的 PIV)和激光散斑测速技术(Laser Speckle Velocimetry, LSV)。当粒子浓度极 低时,可以通过识别、跟踪单个粒子的运动,从所采集的粒子图像中直接测得单 个粒子的位移,这种低粒子密度模式的图像测速方法即为 PTV 技术;当流场中粒 子浓度很高时,以至于粒子在成像系统像平面上形成激光散斑图案(散斑已经掩 盖了真实的粒子图像),这种极高粒子密度模式的图像测速方法即 LSV 技术;PIV 技术则是指粒子浓度较高的成像模式,但尚未在成像系统像面上形成散斑图案, 仍然是真实的粒子图像的图像测量方法,由于此时粒子的识别工作较为困难,只 能获得一小块兴趣区域内多个粒子位移的统计平均值。LSV 技术由于其高粒子浓 度对流场干扰较大,目前已很少采用;PTV 技术由于粒子稀疏,可以通过跟踪单 个粒子的运动轨迹测得速度,比 PIV 测速方法更容易从二维推广到三维,但 PTV 技术所提取的流场速度信息较少,这也限制了它在流场细微结构研究中的应用。 根据粒子图像测速技术原理,PIV系统一般包含四个主要部分:示踪粒子、光 学照明部分、图像采集部分以及图像处理部分。如图1-3所示

图像采集卡 ,摄像机与镜头 图像处理设备 图1-3PIV系统组成 示踪粒子:为了提高透明流体的可测性,布撒示踪粒子用来显示流体的流动状态, 通过测量粒子的运动来获取流场信息。 光学照明部分:在PIV系统中,为了获取较好质量的粒子图像,需要外部辅助光 源的配合,用以增强示踪粒子散射光的强度,一般采用532m的激光光源,有时 也采用高亮的LED光源。 图像采集部分:PIV的核心是图像分析,所以采集到合适的图像十分重要,因此 不仅需要高帧率、高分辨率的摄像机,还需要大带宽、高速的图像记录设备(如 CameraLink高速图像采集记录器)以及相关的信号控制设备。 图像处理部分:将粒子图像进行相关匹配分析、追踪分析等处理,以得到粒子散 斑的运动,该部分功能主要在P℃机上完成。 1.3摄影测量原理 粒子图像测速方法在本质上说是一种摄影测量技术在透明柔性体运动测量 上的一种应用。了解摄影测量的相关知识对于PIV技术的把握具有着重要的意 摄影测量是通过对摄像成像系统拍摄的图像进行分析计算,测量出被测物体 在三维空间中的几何参数和运动参数的一种测量方法。空间物体通过成像系统映 射在相机的像平面上,因此所采集的图像包含了物体的结构信息(PIV中的粒子 图像包含了示踪粒子的空间分布信息与颗粒的尺度信息)。数字图像的最小单位 为像素(Pixl),每个像素的值(灰度信息)反映了空间物体表面对应点的光强 大小,而该点的图像位置对应于空间物体表面的几何位置。物体在像面上的位置 与它的实际物体位置的对应关系可由成像系统的几何投影模型(或称成像模型)
散播示踪粒子的 被测流场 图像采集卡 图像处理设备 摄像机与镜头 光源 图1-3 PIV系统组成 示踪粒子:为了提高透明流体的可测性,布撒示踪粒子用来显示流体的流动状态, 通过测量粒子的运动来获取流场信息。 光学照明部分:在 PIV 系统中,为了获取较好质量的粒子图像,需要外部辅助光 源的配合,用以增强示踪粒子散射光的强度,一般采用 532nm 的激光光源,有时 也采用高亮的 LED 光源。 图像采集部分:PIV 的核心是图像分析,所以采集到合适的图像十分重要,因此 不仅需要高帧率、高分辨率的摄像机,还需要大带宽、高速的图像记录设备(如 CameraLink 高速图像采集记录器)以及相关的信号控制设备。 图像处理部分:将粒子图像进行相关匹配分析、追踪分析等处理,以得到粒子散 斑的运动,该部分功能主要在 PC 机上完成。 1.3 摄影测量原理 粒子图像测速方法在本质上说是一种摄影测量技术在透明柔性体运动测量 上的一种应用。了解摄影测量的相关知识对于 PIV 技术的把握具有着重要的意 义。 摄影测量是通过对摄像成像系统拍摄的图像进行分析计算,测量出被测物体 在三维空间中的几何参数和运动参数的一种测量方法。空间物体通过成像系统映 射在相机的像平面上,因此所采集的图像包含了物体的结构信息(PIV 中的粒子 图像包含了示踪粒子的空间分布信息与颗粒的尺度信息)。数字图像的最小单位 为像素(Pixel),每个像素的值(灰度信息)反映了空间物体表面对应点的光强 大小,而该点的图像位置对应于空间物体表面的几何位置。物体在像面上的位置 与它的实际物体位置的对应关系可由成像系统的几何投影模型(或称成像模型)

所决定。各种摄像测量任务中,都是基于成像映射关系,确定各种几何与运动参 数。从几何角度来看,摄像成像过程是从三维空间向二维空间的映射,是从高维 空间向低维空间的投影。 1.3.1中心透视投影模型 中心透视投影又称为针孔模型是立体视觉系统中常用的一种理想的线性摄 像机模型,是对光学成像几何关系的简化。中心透视投影模型假设物体表面的反 射光或发射光都经过一个“针孔”点而投影在像平面上,这个针孔”点称为光心 也即投影中心或摄影中心。受光的直线传播条件约束,物点、光心和对应像点在 一条直线上。图1-4是中心透视投影模型成像,也就是针孔成像的原理示意图 针孔模型主要由光心、成像面和光轴组成。中心透视投影模型中光心到像面的像 距v称为焦距£,物距u等于光心到物体的距离。 图1-4中心透视投影模型成像几何模型 根据图1-4所示的中心透视投影的几何映射关系,物点P到光轴的距离D与 对应像点p到光轴的距离d之间满足式(1-2)。 D_d (1-2) 1.3.2透镜成像模型 图1-5透镜成像几何模型 根据几何光学的基本原理,理想的凸透镜成像光路如图1-5所示,其中物平 面到透镜中心的距离为物距飞,清晰成像的像平面到透镜中心的距离为像距飞 透镜焦距为R三者满足如式(1-3)所示的成像公式:
所决定。各种摄像测量任务中,都是基于成像映射关系,确定各种几何与运动参 数。从几何角度来看,摄像成像过程是从三维空间向二维空间的映射,是从高维 空间向低维空间的投影。 1.3.1 中心透视投影模型 中心透视投影又称为针孔模型是立体视觉系统中常用的一种理想的线性摄 像机模型,是对光学成像几何关系的简化。中心透视投影模型假设物体表面的反 射光或发射光都经过一个“针孔”点而投影在像平面上,这个针孔”点称为光心, 也即投影中心或摄影中心。受光的直线传播条件约束,物点、光心和对应像点在 一条直线上。图 1-4 是中心透视投影模型成像,也就是针孔成像的原理示意图。 针孔模型主要由光心、成像面和光轴组成。中心透视投影模型中光心到像面的像 距 v 称为焦距 f,物距 u 等于光心到物体的距离。 f v u O 光心 像 物 p P 图 1-4 中心透视投影模型成像几何模型 根据图 1-4 所示的中心透视投影的几何映射关系,物点 P 到光轴的距离 D 与 对应像点 p 到光轴的距离 d 之间满足式(1-2)。 D d u f (1-2) 1.3.2 透镜成像模型 O 光心 像 物 p P F V U 焦点 图 1-5 透镜成像几何模型 根据几何光学的基本原理,理想的凸透镜成像光路如图 1-5 所示,其中物平 面到透镜中心的距离为物距 U,清晰成像的像平面到透镜中心的距离为像距 V, 透镜焦距为 F,三者满足如式(1-3)所示的成像公式:

111 UVF (1-3) 从式(1-2)与式(1-3)的对比中可以看出中心透视投影模型中的焦距与透镜 成像模型中的焦距的概念不同,中心投影模型中所称的焦距实际上是成像平面 到光心的距离,而透镜成像中的焦距指的是光心到透镜焦点之间的距离。由式 (1-3)可得: Fu (1-4) 由式(1-4)可知,当物距远大于像距V时,焦距F≈V,可以用像距来近 似焦距,也就是说,只有当透镜模型的物距远大于焦距和像距时,透镜成像模 型与中心透镜投影模型中的焦距的含义近似一致。因此,使用摄影测量技术对 目标物体进行高精度测量时,不能直接取镜头的标称焦距作为成像模型中的焦 距,而要采用通过摄像机参数标定得到的焦距值。 由于针孔成像光量小,实际成像需要很长的曝光时间,很难得到清晰的图 像,没有实际应用价值。实际成像系统都是使用透镜组组成镜头,可以透过大 量光线并能聚集光线,从而缩短曝光时间和获得清晰的图像。然而,中心透视 投影模型中,物、像、物距、像距(焦距)之间存在有相似三角形联系起来的 几何关系,它可以最佳地反映物与像之间的对应关系,同时又有最简单的表达 形式。所以实际镜头中透镜租的复杂设计都是为了既能大光圈地通过大量的 光,又能尽可能地满足中心透视投影模型的成像关系。 这里需要注意的是,由于镜头设计的复杂性和工艺水平等因素的影响,实 际成像系统不可能严格地满足中心透视投影模型,这种镜头不满足中心透视投 影模型的效应称为镜头畸变。这种主要由镜头畸变使得实际成像位置与根据中 心透视投影模型给出的成像位置之间存在的偏差称之为像差。由于像差的存 在,中心透视投影模型只能是实际成像的一种近似。尤其在使用广角镜头时, 远离图像中心处会有较大的成像畸变,因此实际高精度摄像测量中应尽量采用 考虑了像差的非线性成像模型来描述成像关系。 1.3.3摄彩测量中常用的坐标系 在PIV中所使用的摄像测量技术常用的坐标系为笛卡尔直角坐标系,坐标方 向一般采用右手准则来定义。图16表示了四个不同层次的坐标系统:世界坐标 系、摄像机坐标系、图像物理坐标系以及图像像素坐标系,其定义如下:
1 1 1 U V F (1-3) 从式(1-2)与式(1-3)的对比中可以看出中心透视投影模型中的焦距与透镜 成像模型中的焦距的概念不同,中心投影模型中所称的焦距实际上是成像平面 到光心的距离,而透镜成像中的焦距指的是光心到透镜焦点之间的距离。由式 (1-3)可得: UV F U V (1-4) 由式(1-4)可知,当物距 U 远大于像距 V 时,焦距 F V ,可以用像距来近 似焦距,也就是说,只有当透镜模型的物距远大于焦距和像距时,透镜成像模 型与中心透镜投影模型中的焦距的含义近似一致。因此,使用摄影测量技术对 目标物体进行高精度测量时,不能直接取镜头的标称焦距作为成像模型中的焦 距,而要采用通过摄像机参数标定得到的焦距值。 由于针孔成像光量小,实际成像需要很长的曝光时间,很难得到清晰的图 像,没有实际应用价值。实际成像系统都是使用透镜组组成镜头,可以透过大 量光线并能聚集光线,从而缩短曝光时间和获得清晰的图像。然而,中心透视 投影模型中,物、像、物距、像距(焦距)之间存在有相似三角形联系起来的 几何关系,它可以最佳地反映物与像之间的对应关系,同时又有最简单的表达 形式。所以实际镜头中透镜租的复杂设计都是为了既能大光圈地通过大量的 光,又能尽可能地满足中心透视投影模型的成像关系。 这里需要注意的是,由于镜头设计的复杂性和工艺水平等因素的影响,实 际成像系统不可能严格地满足中心透视投影模型,这种镜头不满足中心透视投 影模型的效应称为镜头畸变。这种主要由镜头畸变使得实际成像位置与根据中 心透视投影模型给出的成像位置之间存在的偏差称之为像差。由于像差的存 在,中心透视投影模型只能是实际成像的一种近似。尤其在使用广角镜头时, 远离图像中心处会有较大的成像畸变,因此实际高精度摄像测量中应尽量采用 考虑了像差的非线性成像模型来描述成像关系。 1.3.3 摄影测量中常用的坐标系 在 PIV 中所使用的摄像测量技术常用的坐标系为笛卡尔直角坐标系,坐标方 向一般采用右手准则来定义。图 1-6 表示了四个不同层次的坐标系统:世界坐标 系、摄像机坐标系、图像物理坐标系以及图像像素坐标系,其定义如下:
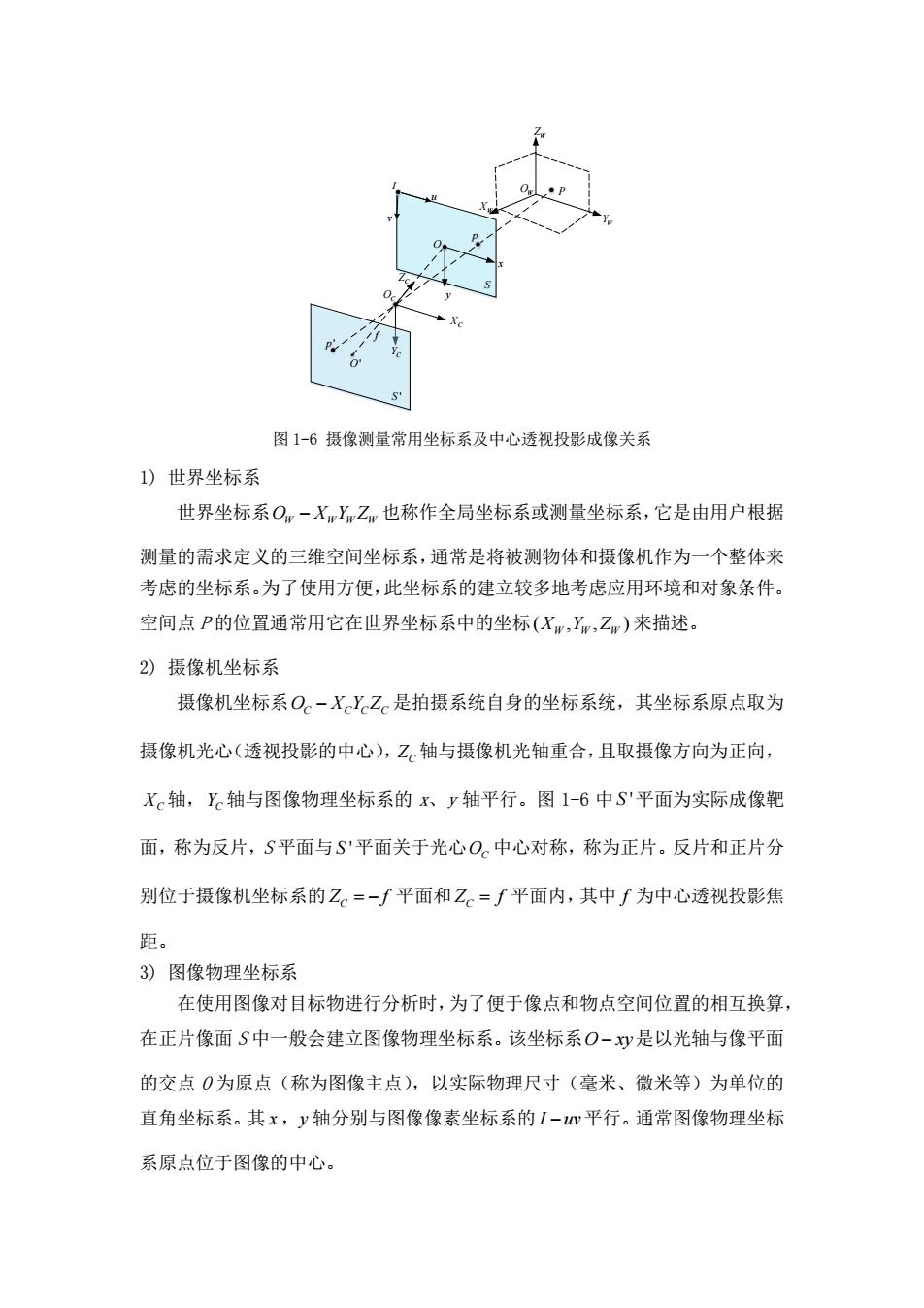
图1-6摄像测量常用坐标系及中心透视投影成像关系 1)世界坐标系 世界坐标系O一XYZ,也称作全局坐标系或测量坐标系,它是由用户根据 测量的需求定义的三维空间坐标系,通常是将被测物体和摄像机作为一个整体来 考虑的坐标系。为了使用方便,此坐标系的建立较多地考虑应用环境和对象条件。 空间点P的位置通常用它在世界坐标系中的坐标(X,Y,Z)来描述。 2)摄像机坐标系 摄像机坐标系O。一XYZ。是拍摄系统自身的坐标系统,其坐标系原点取为 摄像机光心(透视投影的中心),Z。轴与摄像机光轴重合,且取摄像方向为正向, Xc轴,X轴与图像物理坐标系的x、y轴平行。图16中S平面为实际成像靶 面,称为反片,S平面与S平面关于光心O。中心对称,称为正片。反片和正片分 别位于摄像机坐标系的Z。=-∫平面和Z。=∫平面内,其中∫为中心透视投影焦 距。 3)图像物理坐标系 在使用图像对目标物进行分析时,为了便于像点和物点空间位置的相互换算 在正片像面S中一般会建立图像物理坐标系。该坐标系0-y是以光轴与像平面 的交点0为原点(称为图像主点),以实际物理尺寸(毫米、微米等)为单位的 直角坐标系。其x,y轴分别与图像像素坐标系的I-m平行。通常图像物理坐标 系原点位于图像的中心
OC O P XW YW ZW XC YC x y u v p p ' O' OW S S ' I f ZC 图 1-6 摄像测量常用坐标系及中心透视投影成像关系 1) 世界坐标系 世界坐标系 O X Y Z W W W W 也称作全局坐标系或测量坐标系,它是由用户根据 测量的需求定义的三维空间坐标系,通常是将被测物体和摄像机作为一个整体来 考虑的坐标系。为了使用方便,此坐标系的建立较多地考虑应用环境和对象条件。 空间点 P 的位置通常用它在世界坐标系中的坐标 ( , , ) X Y Z W W W 来描述。 2) 摄像机坐标系 摄像机坐标系 O X Y Z C C C C 是拍摄系统自身的坐标系统,其坐标系原点取为 摄像机光心(透视投影的中心),ZC 轴与摄像机光轴重合,且取摄像方向为正向, XC 轴, YC 轴与图像物理坐标系的 x、y 轴平行。图 1-6 中 S ' 平面为实际成像靶 面,称为反片,S 平面与 S ' 平面关于光心 OC 中心对称,称为正片。反片和正片分 别位于摄像机坐标系的 Z f C 平面和 Z f C 平面内,其中 f 为中心透视投影焦 距。 3) 图像物理坐标系 在使用图像对目标物进行分析时,为了便于像点和物点空间位置的相互换算, 在正片像面 S 中一般会建立图像物理坐标系。该坐标系 O xy 是以光轴与像平面 的交点 O 为原点(称为图像主点),以实际物理尺寸(毫米、微米等)为单位的 直角坐标系。其 x ,y 轴分别与图像像素坐标系的 I uv 平行。通常图像物理坐标 系原点位于图像的中心

4)图像像素坐标系 如图16所示,图像像素坐标系1-y是以图像左上角点1为原点,以像素 (Pixel)为坐标单位的直角坐标系。x,y分别表示该像素在数字图像中的列数与 行数,与数字图像像素的常用存储格式一致。图像像素坐标系通常也称为图像坐 标系,该坐标系是进行PIV图像分析程序设计时较为常用的坐标系。 中心透视投影成像的基本关系是所有的成像光线都通过光心,并且物点、像 点和光心三点共线。设物点P在世界坐标系On-XwYrZr中的坐标为 (Xw,Y,Z)。P经过中心透视投影得到的像点P的图像坐标为(化,)。由于存在 像差,实际成像点(代,)与中心透视投影像点(x,)之间会存在偏差,因此,在进 行PIV实验时需要对(住,)进行校正,而点(x,)称为理想像点。 1.3.4二维平面摄像测量 在二维PIV测量中,仅对激光片上的粒子进行追踪,此时有效的粒子均分布 在同一物平面内,即示踪粒子的运动、拓扑变化都在同一平面内,这时用一台摄 像机就可以测量得到各种所需几何结构和运动参数。根据中心透视投影模型,可 以直接导出单台相机测量物平面内目标运动参数的算法。 图1-7单相机平面摄像测量基本原理 如图1-7所示,如果测量平面(如V实验中的激光片)与相机光轴垂直, 即与像面平行,则根据中心透视投影关系可知,目标及其所成的像满足相似关系, 且只相差一个比例系数。此时只要从图像上提取所需目标的几何参数,乘上这个 比例系数,就得到空间物体的实际几何参数。然后再结合序列图像的时间轴信息, 便可以得到物体的运动参数。然而,当物体在同一平面内分布,但此物体平面与 摄像机光轴不垂直时,则不能直接根据一个比例系数便还原物体结构信息。此时 若光轴与物平面的夹角已知,则可以先通过角度投影变换,将图像校正成像面与
4) 图像像素坐标系 如图 1-6 所示,图像像素坐标系 I xy 是以图像左上角点 I 为原点,以像素 (Pixel)为坐标单位的直角坐标系。 x y, 分别表示该像素在数字图像中的列数与 行数,与数字图像像素的常用存储格式一致。图像像素坐标系通常也称为图像坐 标系,该坐标系是进行 PIV 图像分析程序设计时较为常用的坐标系。 中心透视投影成像的基本关系是所有的成像光线都通过光心,并且物点、像 点 和 光 心 三 点 共线。 设 物 点 P 在 世 界坐 标 系 O X Y Z W W W W 中的坐标为 ( , , ) X Y Z W W W 。P 经过中心透视投影得到的像点 p 的图像坐标为 ( , ) x y 。由于存在 像差,实际成像点 ( , ) x y ˆ ˆ 与中心透视投影像点 ( , ) x y 之间会存在偏差,因此,在进 行 PIV 实验时需要对 ( , ) x y ˆ ˆ 进行校正,而点 ( , ) x y 称为理想像点。 1.3.4 二维平面摄像测量 在二维 PIV 测量中,仅对激光片上的粒子进行追踪,此时有效的粒子均分布 在同一物平面内,即示踪粒子的运动、拓扑变化都在同一平面内,这时用一台摄 像机就可以测量得到各种所需几何结构和运动参数。根据中心透视投影模型,可 以直接导出单台相机测量物平面内目标运动参数的算法。 光心 像距 物距 图 1-7 单相机平面摄像测量基本原理 如图 1-7 所示,如果测量平面(如 PIV 实验中的激光片)与相机光轴垂直, 即与像面平行,则根据中心透视投影关系可知,目标及其所成的像满足相似关系, 且只相差一个比例系数。此时只要从图像上提取所需目标的几何参数,乘上这个 比例系数,就得到空间物体的实际几何参数。然后再结合序列图像的时间轴信息, 便可以得到物体的运动参数。然而,当物体在同一平面内分布,但此物体平面与 摄像机光轴不垂直时,则不能直接根据一个比例系数便还原物体结构信息。此时 若光轴与物平面的夹角已知,则可以先通过角度投影变换,将图像校正成像面与

物面平行的情况,使得两者满足相似关系,之后再进行比例变化。 常见的二维平面测量主要有物体二维几何位置、尺寸、形状、变形测量、位 移和速度的测量。其基本原理是利用单幅图像进行目标几何参数测量,或利用不 同时刻在同一角度拍摄的图像,测量图像目标的变化和运动参数。 根据前述内容可知,在二维平面摄像测量中,像与物之间的比例系数的准确 确定至关重要。如果物平面内能够提供某个方向上某对象的已知尺寸,则可以得 到目标在物平面该方向上的几何或运动参数与目标成像之间的比例关系,完成测 量。最常用、简单的方法是在测量物面上放置带有物理尺寸己知的标尺或参照物, 然后在进行摄影测量前先拍照此标尺或参照物,得到此平面测量的比例系数,最 后根据得到的这个比例关系将像素坐标转换为标识物体尺度的物理坐标,这便是 二维摄影测量的一种定标方式。 1.3.5三维交汇测量 如前所述,摄影测量的基本成像模型是中心投影模型(针孔模型)。在满足 针孔模型假设的前提下,像点、光心和物点满足共线方程,即三点共线。对于 单摄像机的情况,如果光心和像点己知,就可以确定一条成像光线,而对应的 物点必然也在此直线上。但是,此时仅能确定成像光线与光轴之间的夹角而无 法确定物点在此直线上的具体位置。因此在没有其他附加条件的约束下,仅用 单个摄像机是无法确定目标的三维位置的。 当使用两台或多台摄像机从不同的角度对同一目标拍摄时,各个摄像机的 光心和其对应同名像点组成的射线应该都通过同一空间物点,即各成像光线应 在物点相交。利用这个原理就可以对空间物点进行交会定位。这就是摄像测量 学三维交会定位的基本原理,也就是三角摄影测量的基本原理。 O,相机1 图18双目交会测量原理 图1-8为两台摄像机对空间某一粒子成像的示意图,该空间粒子为两台摄 像机光心和相应的像点组成的射线的交点。理论上这两射线应该相交与一点。 但是由于实际摄像系统与成像模型之间总存在各种误差,特别是图像上粒子提
物面平行的情况,使得两者满足相似关系,之后再进行比例变化。 常见的二维平面测量主要有物体二维几何位置、尺寸、形状、变形测量、位 移和速度的测量。其基本原理是利用单幅图像进行目标几何参数测量,或利用不 同时刻在同一角度拍摄的图像,测量图像目标的变化和运动参数。 根据前述内容可知,在二维平面摄像测量中,像与物之间的比例系数的准确 确定至关重要。如果物平面内能够提供某个方向上某对象的已知尺寸,则可以得 到目标在物平面该方向上的几何或运动参数与目标成像之间的比例关系,完成测 量。最常用、简单的方法是在测量物面上放置带有物理尺寸已知的标尺或参照物, 然后在进行摄影测量前先拍照此标尺或参照物,得到此平面测量的比例系数,最 后根据得到的这个比例关系将像素坐标转换为标识物体尺度的物理坐标,这便是 二维摄影测量的一种定标方式。 1.3.5 三维交汇测量 如前所述,摄影测量的基本成像模型是中心投影模型(针孔模型)。在满足 针孔模型假设的前提下,像点、光心和物点满足共线方程,即三点共线。对于 单摄像机的情况,如果光心和像点已知,就可以确定一条成像光线,而对应的 物点必然也在此直线上。但是,此时仅能确定成像光线与光轴之间的夹角而无 法确定物点在此直线上的具体位置。因此在没有其他附加条件的约束下,仅用 单个摄像机是无法确定目标的三维位置的。 当使用两台或多台摄像机从不同的角度对同一目标拍摄时,各个摄像机的 光心和其对应同名像点组成的射线应该都通过同一空间物点,即各成像光线应 在物点相交。利用这个原理就可以对空间物点进行交会定位。这就是摄像测量 学三维交会定位的基本原理,也就是三角摄影测量的基本原理。 图 1-8 双目交会测量原理 图 1-8 为两台摄像机对空间某一粒子成像的示意图,该空间粒子为两台摄 像机光心和相应的像点组成的射线的交点。理论上这两射线应该相交与一点。 但是由于实际摄像系统与成像模型之间总存在各种误差,特别是图像上粒子提