第三章测量数据的误差及精度分析 误差理论的基本知识 误差传播定律 衡量精度的指标 权 3 算数平均值计算中误差 误差理论的一些基本应用
第三章 测量数据的误差及精度分析 1 误差理论的基本知识 2 衡量精度的指标 4 误差传播定律 3 算数平均值计算中误差 算数平均值计算中误差 6 误差理论的一些基本应用 5 权权

3.1误差理论的基本知识 大量实践表明,当对某一未知量进行多次观测时,不论 测量仪器多么精密,观测的多么仔细,观测值之间总是存 在差异。 例如:往、返丈量某段距离若干次,或重复观测某一角 度,观测结果都不一致。再如,测量某一平面三角形的三 个内角,其观测值之和常常不等于理论值180°。 对变量进行观测和测量过程中反映出的偏差称为测量误 差。通常把仪器、观测者的技术水平和外界条件三方面称 为观测条件。观测条件相同的各次观测称为等精度观测, 反之称为非精度观测
3.1 误差理论的基本知识 大量实践表明,当对某一未知量进行多次观测时,不论 测量仪器多么精密,观测的多么仔细,观测值之间总是存 在差异。 例如:往、返丈量某段距离若干次,或重复观测某一角 度,观测结果都不一致。再如,测量某一平面三角形的三 个内角,其观测值之和常常不等于理论值180º。 对变量进行观测和测量过程中反映出的偏差称为测量误 差。通常把仪器、观测者的技术水平和外界条件三方面称 为观测条件。观测条件相同的各次观测称为等精度观测, 反之称为非精度观测

3.1.1误差的来源 >观测值的真误差: 真误差=观测值一真值 4=1-L 客观存在(有时未知) 误差来源 0 仪器误差 人的因素 外界环境 观测条件
观测值的真误差: 真误差=观测值-真值 Δ=l - L 3.1.1 误差的来源 客观存在(有时未知) 误差来源 仪器误差 人的因素 外界环境 观测条件

3.1.1误差的来源 (1)仪器误差 测量总是用某种仪器或工具来进行的,仪器或工具不可能十 分完善,因而会对观测结果产生影响。 (2)人的因素 观测或仪器的操作总是需要人来完成,而人的能力是有限 的,会对观测结果带来影响。 (3)外界环境 观测总是在某种特定环境中进行的,且环境在不断变化,因 此会对观测结果造成影响。如电磁波测距会受到空气温度、气 压、湿度、密度分布等的影响。 (4)观测条件 上述仪器条件、人的因素和外界环境的总体称为观测条件或 测量条件
3.1.1 误差的来源 (1) 仪器误差 测量总是用某种仪器或工具来进行的,仪器或工具不可能十 分完善,因而会对观测结果产生影响。 (2) 人的因素 观测或仪器的操作总是需要人来完成,而人的能力是有限 的,会对观测结果带来影响。 (3) 外界环境 观测总是在某种特定环境中进行的,且环境在不断变化,因 此会对观测结果造成影响。如电磁波测距会受到空气温度、气 压、湿度、密度分布等的影响。 (4) 观测条件 上述仪器条件、人的因素和外界环境的总体称为观测条件或 测量条件

3.1.2误差的分类 观测误差按其对测量结果的影响,一般可分为:系统误 差、偶然误差和粗差。 (1)系统误差 系统误差指在相同的观测条件下对某量的一组观测值, 其大小和符号呈现出某种规律性变化的误差。 如:用名义长度为30m的钢尺量距,而该钢尺的实际长 度为30.004m,则每量一尺段会产生-0.004m的系统误差。 系统误差在数值上一般表现为如下几种形式: 1)固定误差项:系统误差的大小和符号保持不变。 2)累积误差项:系统误差随着测量过程不断增加。 3)周期误差项:误差的大小和符号表现为规律性或周期 性的变化
3.1.2 误差的分类 观测误差按其对测量结果的影响,一般可分为:系统误 差、偶然误差和粗差。 (1) 系统误差 系统误差指在相同的观测条件下对某量的一组观测值, 其大小和符号呈现出某种规律性变化的误差。 如:用名义长度为30m的钢尺量距,而该钢尺的实际长 度为30.004m,则每量一尺段会产生-0.004m的系统误差。 系统误差在数值上一般表现为如下几种形式: 1) 固定误差项:系统误差的大小和符号保持不变。 2) 累积误差项:系统误差随着测量过程不断增加。 3) 周期误差项:误差的大小和符号表现为规律性或周期 性的变化

3.1.2误差的分类 (2)粗差 粗差是失误造成的个别大误差,也称错误。主要由于观 测者使用的仪器不合格、观测者的疏忽大意或外界条件发 生意外变动等引起的。 粗差会对最终结果造成很大损害,必须消除。为了杜绝 粗差,除认真仔细作业外,还必须采取必要的检核措施。 例如,对距离进行往、返测量;对角度进行重复观测等。 (3)偶然误差 在相同的观测条件下,对某量进行一系列观测,若误差 出现的大小和符号均不一定,则这种测量误差称为偶然误 差,也称为随机误差
3.1.2 误差的分类 (2) 粗差 粗差是失误造成的个别大误差,也称错误。主要由于观 测者使用的仪器不合格、观测者的疏忽大意或外界条件发 生意外变动等引起的。 粗差会对最终结果造成很大损害,必须消除。为了杜绝 粗差,除认真仔细作业外,还必须采取必要的检核措施。 例如,对距离进行往、返测量;对角度进行重复观测等。 (3) 偶然误差 在相同的观测条件下,对某量进行一系列观测,若误差 出现的大小和符号均不一定,则这种测量误差称为偶然误 差,也称为随机误差
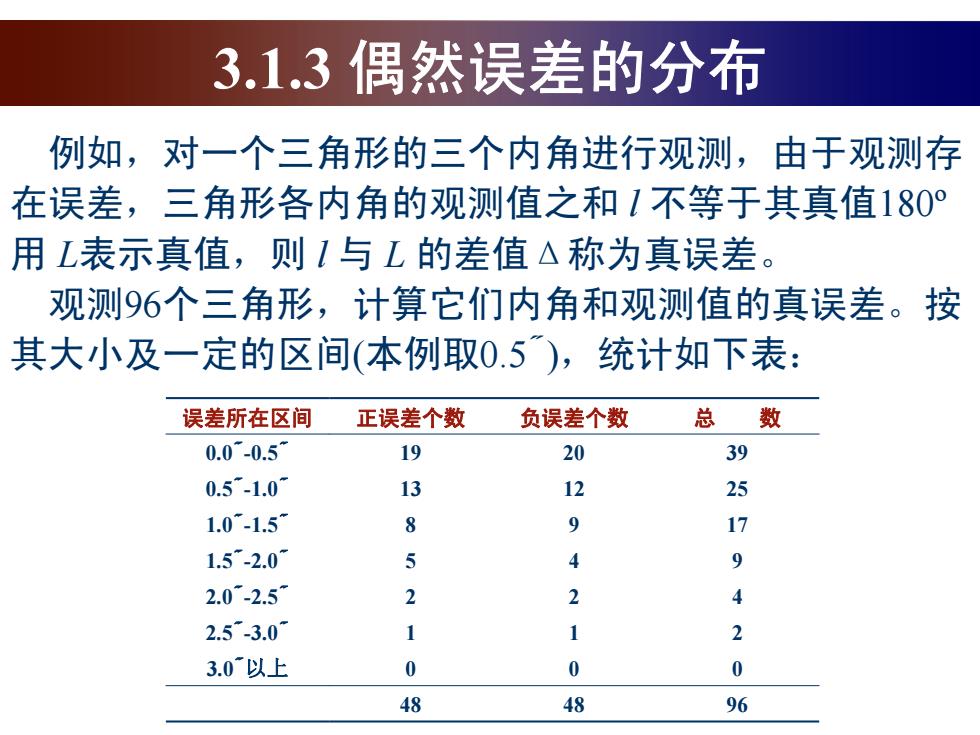
3.1.3偶然误差的分布 例如,对一个三角形的三个内角进行观测,由于观测存 在误差,三角形各内角的观测值之和1不等于其真值180° 用L表示真值,则1与L的差值△称为真误差。 观测96个三角形,计算它们内角和观测值的真误差。按 其大小及一定的区间(本例取0.5),统计如下表: 误差所在区间 正误差个数 负误差个数 总 数 0.0-0.51 19 20 39 0.5-1.0 13 12 25 1.0-1.5 8 9 17 1.5-2.0 5 4 9 2.0-2.5 2 2 4 2.5-3.0 3 3.0以上 0 0 48 48 96
3.1.3 偶然误差的分布 例如,对一个三角形的三个内角进行观测,由于观测存 在误差,三角形各内角的观测值之和 l 不等于其真值180º 用 L表示真值,则 l 与 L 的差值Δ称为真误差。 观测96个三角形,计算它们内角和观测值的真误差。按 其大小及一定的区间(本例取0.5˝),统计如下表: 误差所在区间 正误差个数 负误差个数 总 数 0.0 ˝ -0.5 ˝ 19 20 39 0.5 ˝ -1.0 ˝ 13 12 25 1.0 ˝ -1.5 ˝ 8 9 17 1.5 ˝ -2.0 ˝ 5 4 9 2.0 ˝ -2.5 ˝ 2 2 4 2.5 ˝ -3.0 ˝ 1 1 2 3.0 ˝以上 0 0 0 48 48 96

3.1.3 偶然误差的分布 统计结果一般用频率直方图来表示。以横坐标表示三角 形内角和的偶然误差△,在横坐标轴上自原点向左右截取 误差区间;纵坐标表示各区间内误差出现的相对个数n/n (亦称为频率)除以区间间隔(亦称组距),即频率/组距。 作图时,以横坐标误差区间为底,向上作矩形,使每个 矩形的面积等于该区间误差出现的频率ln。 n:总误差个数,:出现在该区间的误差个数
3.1.3 偶然误差的分布 统计结果一般用频率直方图来表示。以横坐标表示三角 形内角和的偶然误差Δ,在横坐标轴上自原点向左右截取 误差区间;纵坐标表示各区间内误差出现的相对个数 ni/n (亦称为频率)除以区间间隔(亦称组距),即频率/组距。 作图时,以横坐标误差区间为底,向上作矩形,使每个 矩形的面积等于该区间误差出现的频率ni/n。 n:总误差个数,ni:出现在该区间的误差个数

3.1.3偶然误差的分布 显然,图中矩形面积的总和等于1,而每个矩形面积表 示在该区间内偶然误差出现的频率。例如,图中有阴影的 矩形面积,表示误差出现在+0.5”~1.0“之间的频率,其值 为nl/n=13/96=0.136。 如果在相同的观测条件下,观测更多的三角形内角,可 以预期,随着观测次数的不断增多,误差出现在各区间的 频率就趋向一个稳定值一概率。 0-252动5005】051052025西1闭合塑
3.1.3 偶然误差的分布 显然,图中矩形面积的总和等于1,而每个矩形面积表 示在该区间内偶然误差出现的频率。例如,图中有阴影的 矩形面积,表示误差出现在+0.5˝~1.0 ˝之间的频率,其值 为 ni/n=13/96=0.136。 如果在相同的观测条件下,观测更多的三角形内角,可 以预期,随着观测次数的不断增多,误差出现在各区间的 频率就趋向一个稳定值-概率
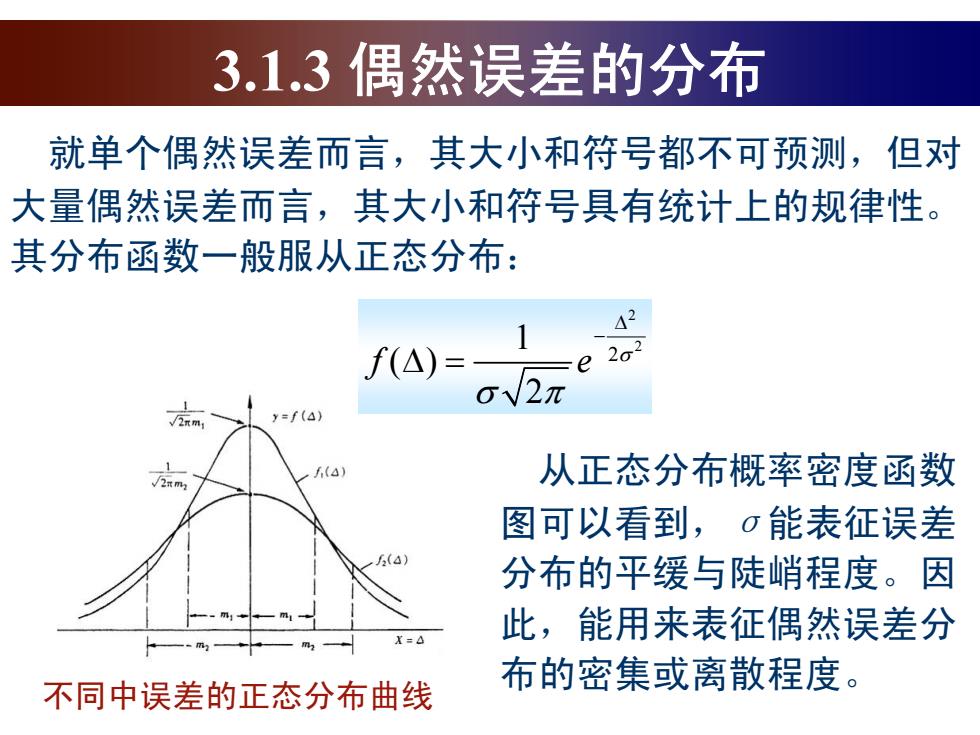
3.1.3偶然误差的分布 就单个偶然误差而言,其大小和符号都不可预测,但对 大量偶然误差而言,其大小和符号具有统计上的规律性。 其分布函数一般服从正态分布: △2 f(△)= 2o2 √2π y=f(4) (4) 从正态分布概率密度函数 图可以看到,σ能表征误差 5(4) 分布的平缓与陡峭程度。因 此,能用来表征偶然误差分 X=△ 不同中误差的正态分布曲线 布的密集或离散程度
不同中误差的正态分布曲线 2 2 2 1 ( ) 2 f e 就单个偶然误差而言,其大小和符号都不可预测,但对 大量偶然误差而言,其大小和符号具有统计上的规律性。 其分布函数一般服从正态分布: 3.1.3 偶然误差的分布 从正态分布概率密度函数 图可以看到, σ能表征误差 分布的平缓与陡峭程度。因 此,能用来表征偶然误差分 布的密集或离散程度