
第二章地面点定位方法 测量基准面与坐标系统 3 数学方法取点空间位置 2 地球曲率的影响 4 水下地形点测量方法
Ѡゴ ഄ䴶⚍ᅮԡᮍ⊩ 1 ⌟䞣ޚ䴶Ϣതᷛ㋏㒳 2 ഄ⧗᳆⥛ⱘᕅડ 33 ᭄ᄺᮍ⊩প⚍ぎ䯈ԡ㕂 4 ∈ϟഄᔶ⚍⌟䞣ᮍ⊩
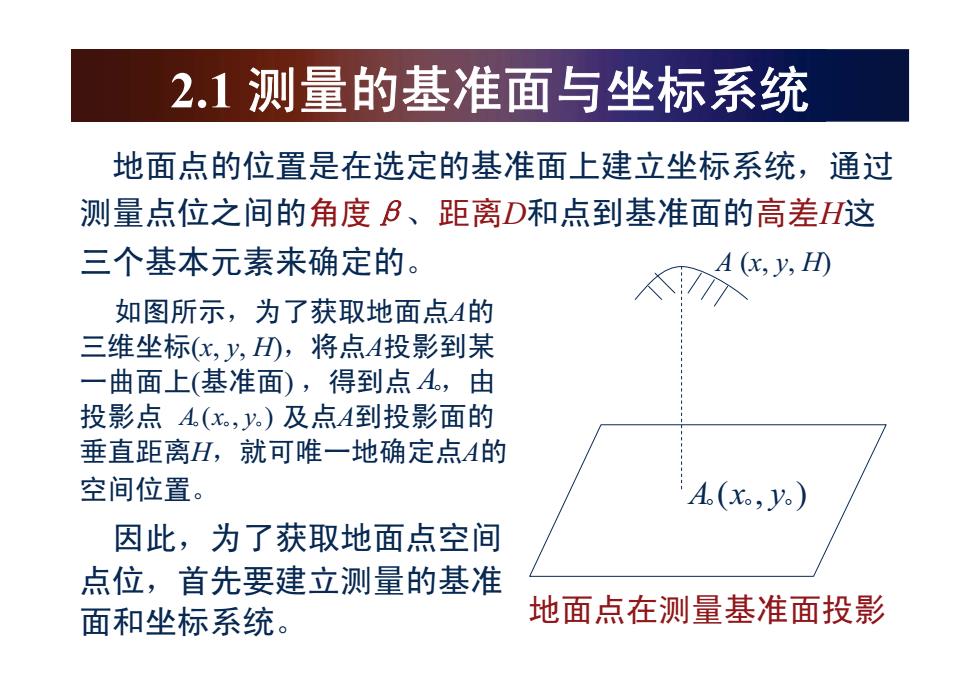
2.1测量的基准面与坐标系统 地面点的位置是在选定的基准面上建立坐标系统,通过 测量点位之间的角度B、距离D和点到基准面的高差H这 三个基本元素来确定的。 A (x,y,H) 如图所示,为了获取地面点A的 三维坐标(x,y,H),将点A投影到某 一曲面上(基准面),得到点A。,由 投影点A(x。,y.)及点A到投影面的 垂直距离H,就可唯一地确定点A的 空间位置。 A(x。,) 因此,为了获取地面点空间 点位,首先要建立测量的基准 面和坐标系统。 地面点在测量基准面投影
2.1 ⌟䞣ⱘޚ䴶Ϣതᷛ㋏㒳 ഄ䴶⚍ⱘԡ㕂ᰃ䗝ᅮⱘޚ䴶Ϟᓎゟതᷛ㋏㒳ˈ䗮䖛 ⌟䞣⚍ԡП䯈ⱘ㾦ᑺ£ǃ䎱⾏D⚍ࠄޚ䴶ⱘ催ᏂH䖭 ϝϾᴀܗ㋴ᴹ⹂ᅮⱘDŽ བ᠔⼎ˈЎњ㦋পഄ䴶⚍Aⱘ ϝ㓈തᷛ(x, y, H)ˈᇚ⚍Aᡩᕅࠄᶤ ϔ᳆䴶Ϟ(ޚ䴶) ˈᕫࠄ⬅ˈ ⚍ ᡩᕅ⚍ ঞ⚍Aࠄᡩᕅ䴶ⱘ ൖⳈ䎱⾏Hˈህৃଃϔഄ⹂ᅮ⚍Aⱘ ぎ䯈ԡ㕂DŽ A A (, ) x y ℸˈЎњ㦋পഄ䴶⚍ぎ䯈 ⚍ԡˈ佪ܜ㽕ᓎゟ⌟䞣ⱘޚ 䴶തᷛ㋏㒳DŽ A (x, y, H) A (, ) x y ഄ䴶⚍⌟䞣ޚ䴶ᡩᕅ�������

2.1测量的基准面与坐标系统 基准面的选择对点位的确定有着关键作用,它是空间点 平面位置定位的前提条件。 在地球表面进行点位测量时,如果将投影曲面作为基准 面,应该具备两个基本条件: ()其形状和大小能与地球总形体相拟合; (2)必须是一个能用简单几何体和方程式描述的规则数学 面,并有利于数据处理
ഄ⧗㸼䴶䖯㸠⚍ԡ⌟䞣ᯊˈབᵰᇚᡩᕅ᳆䴶Ўޚ 䴶ˈᑨ䆹ϸϾᴀᴵӊ˖ (1) ݊ᔶ⢊ᇣ㛑Ϣഄ⧗ᘏᔶԧⳌᢳড়˗ (2) ᖙ乏ᰃϔϾ㛑⫼ㅔऩԧԩᮍᓣᦣ䗄ⱘ㾘᭄߭ᄺ 䴶ˈᑊ᳝߽Ѣ᭄໘⧚DŽ ޚ䴶ⱘ䗝ᢽᇍ⚍ԡⱘ⹂ᅮ᳝ⴔ݇䬂⫼ˈᅗᰃぎ䯈⚍ ᑇ䴶ԡ㕂ᅮԡⱘࠡᦤᴵӊDŽ 2.1 ⌟ 䞣 ⱘ ޚ 䴶 Ϣ ത ᷛ ㋏ 㒳

2.1.1测量基准面 测量工作是在地球表面上进行的,而地球自然表面很不 规则,上面分布有江河湖海,平原丘陵和高山深谷,其中 海洋占地球表面积的71%,陆地占地球表面积的29%。 马里亚纳海沟(-11022m) 两者的高差与地球半径(6371km) 珠穆朗玛峰 相比,可以忽略不计。 (8844.43m)
2.1.1 ⌟䞣ޚ䴶 ⌟䞣Ꮉᰃഄ⧗㸼䴶Ϟ䖯㸠ⱘˈ㗠ഄ⧗㞾✊㸼䴶ᕜϡ 㾘߭ˈϞ䴶ߚᏗ᳝∳⊇⍋ˈᑇॳϬ䱉催ቅ⏅䈋ˈ݊Ё ⍋⋟ऴഄ⧗㸼䴶⿃ⱘ71%ˈ䰚ഄऴഄ⧗㸼䴶⿃ⱘ29%DŽ ϸ㗙ⱘ催ᏂϢഄ⧗ञᕘ(6371km) Ⳍ↨ˈৃҹᗑ⬹ϡ䅵DŽ 偀䞠Ѯ㒇⍋≳ (-11022m) ⦴〚ᳫ⥯ዄ (8844.43m)

2.1.1测量基准面 在测量学中,通常把静止的水面称 为水准面。 海水水位是动态的,因此,水准面 有无穷多个,通常把通过平均海水面 并向大陆、岛屿延伸而形成的闭合曲 大地水准面 面称为大地水准面。大地水准面是测 量工作的基准面。 在地球重力场中水准面处处与重力方向正交,重力的方 向线称为铅垂线,它是测量工作的基准线
⌟䞣ᄺЁˈ䗮ᐌᡞ䴭ℶⱘ∈䴶⿄ Ў∈ޚ䴶 DŽ ⍋∈∈ԡᰃࡼᗕⱘˈℸˈ∈ޚ䴶 ᳝᮴かϾˈ䗮ᐌᡞ䗮䖛ᑇഛ⍋∈䴶 ᑊ䰚ǃቯቓᓊԌ㗠ᔶ៤ⱘ䯁ড়᳆ 䴶⿄Ўഄ∈ޚ䴶DŽഄ∈ޚ䴶ᰃ⌟ 䞣Ꮉⱘޚ䴶 DŽ ഄ⧗䞡എЁ∈ޚ䴶໘໘Ϣ䞡ᮍℷѸˈ䞡ⱘᮍ 㒓⿄Ў䪙ൖ㒓ˈᅗᰃ⌟䞣Ꮉⱘޚ㒓 DŽ 䴶ޚ∋ഄ 2.1.1 ⌟ 䞣 ޚ 䴶
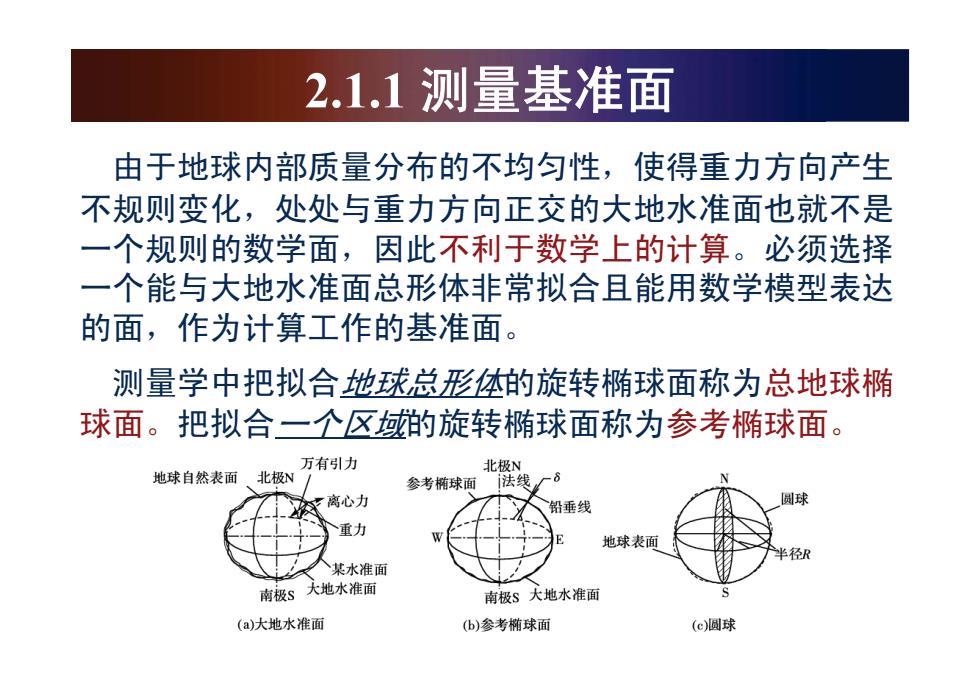
2.1.1测量基准面 由于地球内部质量分布的不均匀性,使得重力方向产生 不规则变化,处处与重力方向正交的大地水准面也就不是 一个规则的数学面,因此不利于数学上的计算。必须选择 一个能与大地水准面总形体非常拟合且能用数学模型表达 的面,作为计算工作的基准面。 测量学中把拟合地球总形体的旋转椭球面称为总地球椭 球面。把拟合一个区域的旋转椭球面称为参考椭球面。 万有引力 北极N 地球自然表面。北极N 参考椭球面法线 离心力 铅垂线 重力 地球表面 半径R 某水准面 南极S 大地水准面 南极S大地水准面 (a)大地水准面 (凸)参考椭球面 (c)圆球
⬅Ѣഄ⧗ݙ䚼䋼䞣ߚᏗⱘϡഛࣔᗻˈՓᕫ䞡ᮍѻ⫳ ϡ㾘߭ব࣪ˈ໘໘Ϣ䞡ᮍℷѸⱘഄ∈ޚ䴶гህϡᰃ ϔϾ㾘߭ⱘ᭄ᄺ䴶ˈℸϡ߽Ѣ᭄ᄺϞⱘ䅵ㅫDŽᖙ乏䗝ᢽ ϔϾ㛑Ϣഄ∈ޚ䴶ᘏᔶԧ䴲ᐌᢳড়Ϩ㛑⫼᭄ᄺൟ㸼䖒 ⱘ䴶ˈЎ䅵ㅫᎹⱘޚ䴶DŽ ⌟䞣ᄺЁᡞᢳড়ഄ⧗ᘏᔶԧⱘᮟ䕀ἁ⧗䴶⿄Ўᘏഄ⧗ἁ ⧗䴶DŽᡞᢳড়ϔϾऎඳⱘᮟ䕀ἁ⧗䴶⿄Ўখ㗗ἁ⧗䴶DŽ 2.1.1 ⌟ 䞣 ޚ 䴶

2.1.1测量基准面 我国坐标目前采用的“80西安坐标”(80国家大地坐标) 我国目前采用的高程基准面是“1985年国家高程基准”, 它是根据青岛验潮站1952~1979年观测资料确定的黄海平 均海水面(其高程为零)作为起算的高程系统,并在青岛观 象山建立了固定水准原点,其高程为72.260m。 永乐镇大地原点 观象山黄海水准原点
៥തᷛⳂࠡ䞛⫼ⱘ“80㽓ᅝതᷛ”˄80ᆊഄതᷛ˅ ៥Ⳃࠡ䞛⫼ⱘ催ޚ䴶ᰃ“1985ᑈᆊ催ޚˈ“ ᅗᰃḍ䴦ቯ偠╂キ1952~1979ᑈ㾖⌟䌘᭭⹂ᅮⱘ咘⍋ᑇ ഛ⍋∈䴶(݊催Ў䳊)Ў䍋ㅫⱘ催㋏㒳ˈᑊ䴦ቯ㾖 䈵ቅᓎゟњᅮ∈ޚ݊ˈ⚍ॳ催Ў72.260mDŽ ⚍ॳޚ∋㾖䈵ቅ咘⍋ 2.1.1 ⌟䞣ޚ䴶 ∌Ф䬛ഄॳ⚍
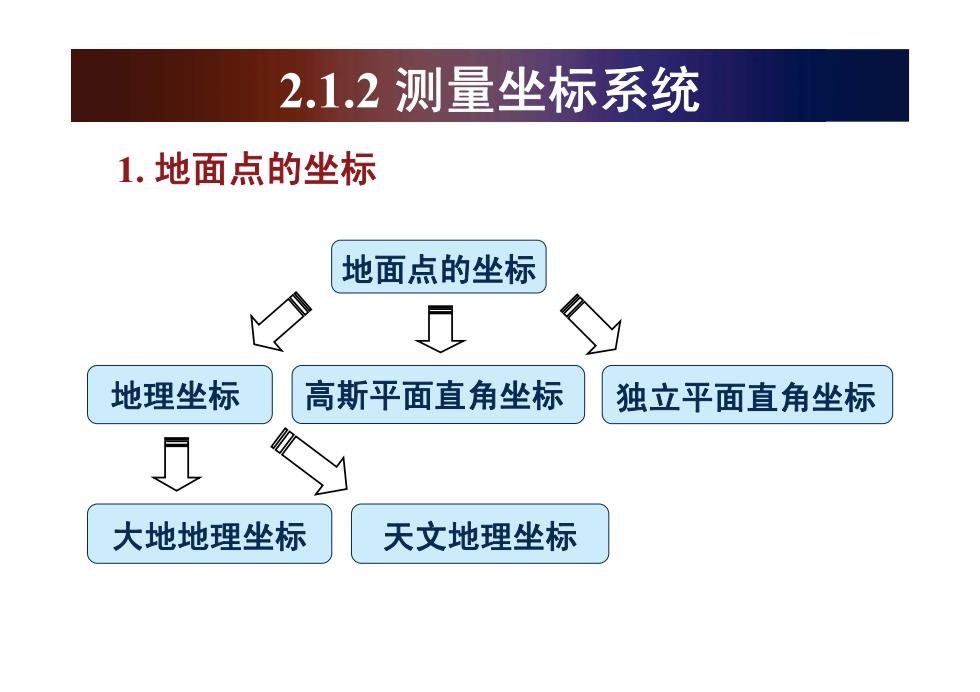
2.1.2测量坐标系统 1.地面点的坐标 地面点的坐标 地理坐标 高斯平面直角坐标 独立平面直角坐标 大地地理坐标 天文地理坐标
2.1.2 ⌟䞣തᷛ㋏㒳 1. ഄ䴶⚍ⱘതᷛ ഄ䴶⚍ⱘതᷛ ഄ⧚തᷛ 催ᮃᑇ䴶Ⳉ㾦തᷛ ⣀ゟᑇ䴶Ⳉ㾦തᷛ ഄഄ⧚തᷛ ᭛ഄ⧚തᷛ

2.1.2测量坐标系统 ()地理坐标: 二位置的坐标系统。 子午面:地面点与 赤道面:通过地心 Q 油的平面。 赤道 子午线:子午面与 0 赤道:赤道面与 经度L:过地球面 KP1与过伦敦格林尼 治天文台的首子午 面角。经度由首子午 面起算,在东半球 0 为西经。 纬度B:过球面某 首 K赤道 戋OL与赤道面EMKO 的夹角
䌸䘧䴶˖䗮䖛ഄᖗOൖⳈѢഄ⧗㞾䕀䕈ⱘᑇ䴶DŽ ᄤज䴶˖ഄ䴶⚍Ϣഄ⧗फ࣫ᵕⱘ݅䴶DŽ ᄤज㒓˖ᄤज䴶Ϣഄ⧗㸼䴶ⳌѸⱘ㒓DŽ 䌸 䘧˖䌸䘧䴶Ϣഄ⧗㸼䴶ⳌѸⱘ㒓DŽ 㒣ᑺL ˖䖛ഄ⧗䴶ᶤ⚍Lⱘᄤज䴶 PLKP1 Ϣ䖛ӺᬺḐᵫሐ ⊏᭛ৄⱘ佪ᄤज䴶 PMP1 㒘៤ⱘѠ䴶㾦DŽ㒣ᑺ⬅佪ᄤज 䴶䍋ㅫˈϰञ⧗Ўϰ㒣ˈ㽓ञ⧗Ў㽓㒣DŽ 㒀ᑺB ˖䖛⧗䴶ᶤ⚍Lⱘ⊩㒓䪙ൖ㒓OLϢ䌸䘧䴶EMKQ ⱘ།㾦DŽ 2.1.2 ⌟䞣തᷛ㋏㒳 (1) ഄ⧚തᷛ˖㸼⼎ഄ䴶⚍⧗䴶Ϟԡ㕂ⱘതᷛ㋏㒳DŽ

2.1.2测量坐标系统 赤道 地理坐标
2.1.2 ⌟䞣തᷛ㋏㒳 ഄ⧚തᷛ