
固定管板换热器壳体应力测定实验 一、实验目的 1.了解换热器壳体在壳程压力作用下产生的应力: 2.了解换热器壳体在压力和温度载荷联合作用下产生的应力: 3.掌握电阻应变片测定应力的原理和方法,熟悉有关应力测定仪器 二、实验装置 过程设备与控制多功能综合实验台,BZ2205C静态电阻应变仪 三、实验内容 测定在壳程压力作用下换热器壳体上的应力,以壳程压力为横坐标,壳体应 力为纵坐标,作σ。一P,的理论与实验曲线,并进行分析:测定在压力和温度载 荷联合作用下换热器壳体上的应力,以温差为横坐标,壳体应力为纵坐标,作 O.-△1实验曲线,并进行分析。 四、实验步骤 (一)应变仪操作: 1.检查各接线是否正确、牢固: 2.打开应变仪电源,预热20分钟: 3.设置测量桥路为1/4桥: 4.设定灵敏系数,本实验中,应变片的灵敏系数为2.07: 5.设置公共补偿点: 6.设置补偿点补偿10个测量点: 7.清空历史数据: 8.确认上述设置有效: 9.进行电桥平衡。 (二)实验台和控制台操作 1.打开冷流体壳程入口阀下7、冷流体壳程出口阀8,关闭其它阀门,使冷流 体走壳程: 2.打开自来水阀门灌泵,保证离心泵中充满水,开排气阀放净空气,关闭自来 水阀门:
固定管板换热器壳体应力测定实验 一、实验目的 1.了解换热器壳体在壳程压力作用下产生的应力; 2.了解换热器壳体在压力和温度载荷联合作用下产生的应力; 3.掌握电阻应变片测定应力的原理和方法,熟悉有关应力测定仪器。 二、实验装置 过程设备与控制多功能综合实验台,BZ2205C 静态电阻应变仪 三、实验内容 测定在壳程压力作用下换热器壳体上的应力,以壳程压力为横坐标,壳体应 力为纵坐标,作σ θ − ps 的理论与实验曲线,并进行分析;测定在压力和温度载 荷联合作用下换热器壳体上的应力,以温差为横坐标,壳体应力为纵坐标,作 t σ z − Δ 实验曲线,并进行分析。 四、实验步骤 (一)应变仪操作: 1.检查各接线是否正确、牢固; 2.打开应变仪电源,预热 20 分钟; 3.设置测量桥路为 1/4 桥; 4.设定灵敏系数,本实验中,应变片的灵敏系数为 2.07; 5.设置公共补偿点; 6.设置补偿点补偿 10 个测量点; 7.清空历史数据; 8.确认上述设置有效; 9.进行电桥平衡。 (二)实验台和控制台操作 1.打开冷流体壳程入口阀 F7、冷流体壳程出口阀 F8,关闭其它阀门,使冷流 体走壳程; 2.打开自来水阀门灌泵,保证离心泵中充满水,开排气阀放净空气,关闭自来 水阀门;
3.向右扳动控制台面板上的总控开关“14”,启动控制台: 4.流量自动/手动控制按钮“3”置于手动位置,顺时针旋转“9”旋钮,打开 电动调节阀: 5.启动组态王程序,进入实验二“换热器壳体应力测定实验”画面,选择“壳 体受压”: 6.扳动选择开关“7”,将水泵运行设置成直接启动方式(全速运行方式): 7.按下冷水泵启动按钮“11”,冷水泵开始运转: 8.清空数据库: 9.调节流量调节阀F6,使压力从0.6到0.9wPa,每隔0.1MPa测量和记录一次: 10.关闭冷水泵,打开热流体管程入口阀下1、热流体管程出口阀2,使热流体 走管程,冷流体走壳程: 11.选择“热应力”,清空数据库按下冷水泵启动按纽“11”,冷水泵开始运转: 12.调节流量调节阀6,使壳程流体压力保持在某一固定的值不变: 13.顺时针旋转热水泵启动旋钮“13”,启动热水泵: 14.改变温度,选三个不同的温度(温差间隔在10℃左右),测量并记录一次: 15.实验结束后,关闭冷、热水泵,进入“换热器壳体应力测定实验数据处理” 程序: 16.点击“导入数据”按钮,选择处理数据文件的类型为1一数据库文件,点击 “计算”按钮,进行数据计算,点击“绘图”按钮,生成实验曲线: 17.点击“导出数据”按钮,可生成实验数据文本文件,输入文件名称及文件类 型后,按“保存”按钮,保存数据文件: 18.点击“打印”按钮,打印实验数据和实验曲线: 19.点击“退出”按钮,退出实验程序。 壳程压力引起的壳体应力(只有冷水走壳程) 表1实验测量结果 P (MPa) p (MPa) 测点 6. 1 3 4 5
3.向右扳动控制台面板上的总控开关“14”,启动控制台; 4.流量自动/手动控制按钮“3”置于手动位置,顺时针旋转“9”旋钮,打开 电动调节阀; 5.启动组态王程序,进入实验二“换热器壳体应力测定实验”画面,选择“壳 体受压”; 6.扳动选择开关“7”,将水泵运行设置成直接启动方式(全速运行方式); 7.按下冷水泵启动按钮“11”,冷水泵开始运转; 8.清空数据库; 9.调节流量调节阀 F6,使压力从 0.6 到 0.9MPa,每隔 0.1MPa 测量和记录一次; 10.关闭冷水泵,打开热流体管程入口阀 F1、热流体管程出口阀 F2,使热流体 走管程,冷流体走壳程; 11. 选择“热应力” ,清空数据库按下冷水泵启动按钮“11”,冷水泵开始运转; 12. 调节流量调节阀 F6, 使壳程流体压力保持在某一固定的值不变; 13.顺时针旋转热水泵启动旋钮“13”,启动热水泵; 14.改变温度,选三个不同的温度(温差间隔在 10℃左右),测量并记录一次; 15.实验结束后,关闭冷、热水泵,进入“换热器壳体应力测定实验数据处理” 程序; 16.点击“导入数据”按钮,选择处理数据文件的类型为 1-数据库文件,点击 “计算”按钮,进行数据计算,点击“绘图”按钮,生成实验曲线; 17.点击“导出数据”按钮,可生成实验数据文本文件,输入文件名称及文件类 型后,按“保存”按钮,保存数据文件; 18.点击“打印”按钮,打印实验数据和实验曲线; 19.点击“退出”按钮,退出实验程序。 壳程压力引起的壳体应力(只有冷水走壳程) 表 1 实验测量结果 psi ( MPa ) pso ( MPa ) 测 点 θ ε z ε 1 2 3 4 5

3 1 2 3 4 5 4 5 表2实验计算结果 测点 P (MPa) Go (MPa)
1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 表 2 实验计算结果 测点 Ps (MPa ) θ ε z ε σ θ (MPa ) 1 2 3 4
压力和温度载荷联合作用引起的壳体应力(热水走管程、冷水走壳程) 表3实验测量结果 p测 (C)(C)(C)(C)(MPa)(MPa)(MPa)(MPa) 1 2 3 5 1 2 4 5 1 3 5 表4验计算结果 测点 1,(C) 1,(C) Ar (C)
5 压力和温度载荷联合作用引起的壳体应力(热水走管程、冷水走壳程) 表 3 实验测量结果 T1 (°C ) T2 (°C ) 1t (°C ) 2t (°C ) pti ( MPa ) pto ( MPa ) psi ( MPa ) pso ( MPa ) 测 点 θ ε z ε 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 表 4 验计算结果 测点 t t (°C ) s t (°C ) Δt (°C ) 1

表5验计算结果 测点 Ar (C) G:(MPa) 五、思考题 1.构件中产生热应力的条件是什么?
2 3 4 5 表 5 验计算结果 测点 Δt (°C ) θ ε z ε σ z ( MPa ) 1 2 3 4 5 五、思考题 1.构件中产生热应力的条件是什么?

2.固定管板换热器中的热应力是否可以消除?是否可以采取措施降低热应力? 3.只受壳程压力作用下,壳体上的轴向应力远小于环向应力,为什么? 六、实验基本原理 1.应力测定中常采用电阻应变仪来测定各点的应变值,然后根据广义虎克定律 换算成相应的应力值。由于换热器壳体受力后可认为是处于二向应力状态,于是 在弹性范围内可用广义虎克定律表示如下: E 轴向应力:,1-6+, (1) E 环向应九:,1,+,) (2) 式中E和4分别为设备材料的弹性模量和泊松比,6,和5。分别为轴向应变和环 向应变,。,和σ。分别为轴向应力和环向应力。 2.电阻应变仪的基本原理是将应变片电阻的微小变化,通过电桥转换成电压的 变化。其过程为: s应变片,B电桥→Av咸A)放大器, R 将A俄△W放大检流计或纪录仪→指示或纪录 我们将应变片粘贴在换热器壳体外壁面上,使它与换热器壳体一起变形。换热 器壳体的伸长或压缩变形将引起应变片电阻值的变化,它们之间有如下关系: △R1=K△=KE R, (3) 式中:K一电阻应变片的灵敏系数: e—试件的应变: △R—电阻应变片电阻值的改变值 R一电阻应变片电阻值未变形时的电阻值
2.固定管板换热器中的热应力是否可以消除?是否可以采取措施降低热应力? 3.只受壳程压力作用下,壳体上的轴向应力远小于环向应力,为什么? 六、实验基本原理 1.应力测定中常采用电阻应变仪来测定各点的应变值,然后根据广义虎克定律 换算成相应的应力值。由于换热器壳体受力后可认为是处于二向应力状态,于是 在弹性范围内可用广义虎克定律表示如下: 轴向应力: 2 ( ) 1 z z E σ θ ε με μ = + − (1) 环向应力: 2 ( ) 1 z E σ θ θ ε με μ = + − (2) 式中 E 和 μ 分别为设备材料的弹性模量和泊松比, z ε 和 θ ε 分别为轴向应变和环 向应变,σ z 和σθ分别为轴向应力和环向应力。 2.电阻应变仪的基本原理是将应变片电阻的微小变化,通过电桥转换成电压的 变化。其过程为: 将 ( ) 指示或纪录 检流计或纪录仪 Δν 或ΔI 放大 → 我们将应变片粘贴在换热器壳体外壁面上,使它与换热器壳体一起变形。换热 器壳体的伸长或压缩变形将引起应变片电阻值的变化,它们之间有如下关系: (3) 式中: K ——电阻应变片的灵敏系数; ε ——试件的应变; ΔR1——电阻应变片电阻值的改变值; R1——电阻应变片电阻值未变形时的电阻值。 ( ) dR I R ε ν → →Δ Δ → 应变片 电桥 放大器 或 1 1 R l K K R L ε Δ Δ = =⋅

换热器壳体应力的实验测定和理论计算 (一)只受壳程压力载荷 (1)实测应力计算 壳程流体压力取壳程流体进出口压力的平均值: R=B+2 2 (4) 式中:P一壳程流体压力: P一壳程流体进口压力: P。一壳程流体出口压力。 作8:-P和8。-P关系曲线,并进行线性拟合。因为当P.=0时,6.=0,6。=0, 可得应变与压力的关系为: 6:=P,6g=1P: 根据式(41)和(42)可以求出应力值。由此能求出各种压力下的应力和应变。 (2)理论应力计算 壳体中环向应力o。由下式计算: o。sB2 21 (5) 式中:D一壳体内径,D=207mm: 1一壳体壁厚,1=6mm。 壳体中轴向应力σ:计算比较复杂,它包括作用在管板上的流体压力引起的 轴向应力以及壳体在压力作用下的经向变形所引起的轴向应力(泊松效应,注意 壳体和管子及管板构成了静不定系统),且和管板的变形有关,这里不作计算。 (二)受壳程压力和温度载荷联合作用 在正常操作条件下,换热器壳体中的应力是流体压力载荷(壳程压力P,、 管程压力P,)、温度载荷及重力与支座反力所引起的。由于换热器的轴向弯曲 刚度大,重力与支座反力在壳体上产生的弯曲应力相对较小,所以可以忽略。 因为温度载荷只引起轴向应力,所以当压力载荷和温度载荷联合作用时有: 0:=0+a (6) 0g=08 (7)
换热器壳体应力的实验测定和理论计算 (一)只受壳程压力载荷 (1)实测应力计算 壳程流体压力取壳程流体进出口压力的平均值: (4) 式中: Ps ——壳程流体压力; Psi ——壳程流体进口压力; Pso ——壳程流体出口压力。 作 z − Ps ε 和 θ − Ps ε 关系曲线,并进行线性拟合。因为当 Ps = 0时,ε z = 0,ε θ = 0, 可得应变与压力的关系为: ε z s = λ1P , θ 2Ps ε = λ ; 根据式(4-1)和(4-2)可以求出应力值。由此能求出各种压力下的应力和应变。 (2)理论应力计算 壳体中环向应力σ θ由下式计算: (5) 式中: Di ——壳体内径, D =i 207mm; t ——壳体壁厚, t = 6mm。 壳体中轴向应力σ z 计算比较复杂,它包括作用在管板上的流体压力引起的 轴向应力以及壳体在压力作用下的经向变形所引起的轴向应力(泊松效应,注意 壳体和管子及管板构成了静不定系统),且和管板的变形有关,这里不作计算。 (二)受壳程压力和温度载荷联合作用 在正常操作条件下,换热器壳体中的应力是流体压力载荷(壳程压力 s p 、 管程压力 pt )、温度载荷及重力与支座反力所引起的。由于换热器的轴向弯曲 刚度大,重力与支座反力在壳体上产生的弯曲应力相对较小,所以可以忽略。 因为温度载荷只引起轴向应力,所以当压力载荷和温度载荷联合作用时有: (6) (7) 2 si so s P P P + = 2 s i p D t σ θ = p t σ zz z = σ σ+ p σ θ = σ θ
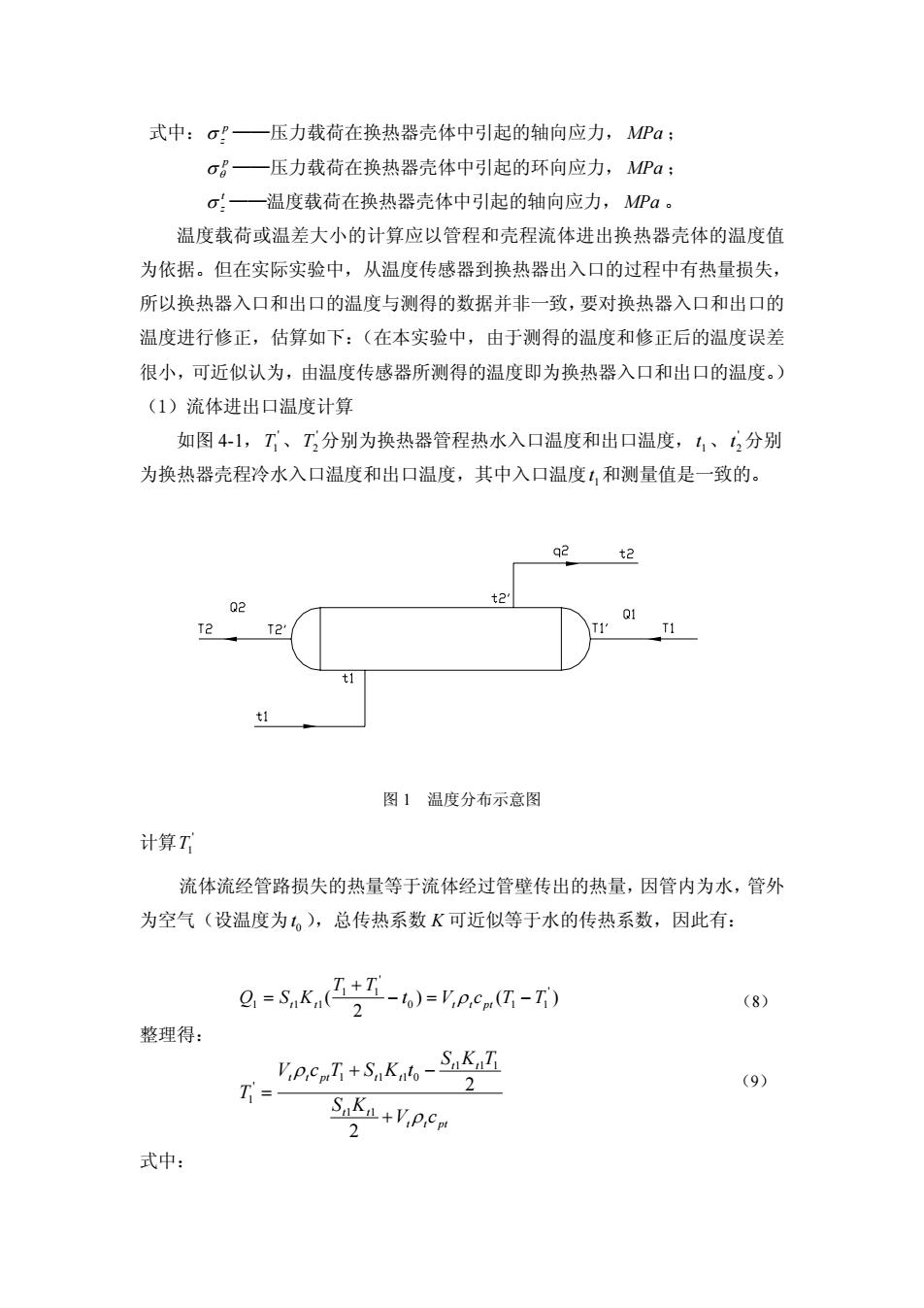
式中:σP一压力载荷在换热器壳体中引起的轴向应力,MPa: σB一压力载荷在换热器壳体中引起的环向应力,MPa: o:—温度载荷在换热器壳体中引起的轴向应力,MPa。 温度载荷或温差大小的计算应以管程和壳程流体进出换热器壳体的温度值 为依据。但在实际实验中,从温度传感器到换热器出入口的过程中有热量损失 所以换热器入口和出口的温度与测得的数据并非一致,要对换热器入口和出口的 温度进行修正,估算如下:(在本实验中,由于测得的温度和修正后的温度误差 很小,可近似认为,由温度传感器所测得的温度即为换热器入口和出口的温度。》 (1)流体进出口温度计算 如图41,T、T分别为换热器管程热水入口温度和出口温度,1、,分别 为换热器壳程冷水入口温度和出口温度,其中入口温度1和测量值是一致的。 q2 t2 T1 、 图1温度分布示意图 计算T 流体流经管路损失的热量等于流体经过管壁传出的热量,因管内为水,管外 为空气(设温度为。),总传热系数K可近似等于水的传热系数,因此有: g=Sk4工-6)=pcng-T0 2 (8) 整理得: T= pcI+SK6-Sk☑ (9) SaKn+VPCm 2 式中:
式中: p σ z ——压力载荷在换热器壳体中引起的轴向应力,MPa ; p σ θ ——压力载荷在换热器壳体中引起的环向应力,MPa ; t σ z ——温度载荷在换热器壳体中引起的轴向应力,MPa 。 温度载荷或温差大小的计算应以管程和壳程流体进出换热器壳体的温度值 为依据。但在实际实验中,从温度传感器到换热器出入口的过程中有热量损失, 所以换热器入口和出口的温度与测得的数据并非一致,要对换热器入口和出口的 温度进行修正,估算如下:(在本实验中,由于测得的温度和修正后的温度误差 很小,可近似认为,由温度传感器所测得的温度即为换热器入口和出口的温度。) (1)流体进出口温度计算 如图 4-1, ' T1 、 ' T2分别为换热器管程热水入口温度和出口温度, 1t 、 ' 2t 分别 为换热器壳程冷水入口温度和出口温度,其中入口温度 1t 和测量值是一致的。 图 1 温度分布示意图 计算 ' T1 流体流经管路损失的热量等于流体经过管壁传出的热量,因管内为水,管外 为空气(设温度为 0t ),总传热系数 K 可近似等于水的传热系数,因此有: (8) 整理得: (9) 式中: ' 1 1 ' 1 11 0 1 1 ( ) () 2 t t t t pt T T Q SK t V c T T ρ + = −= − 1 11 1 1 10 ' 1 1 1 2 2 t t t t pt t t t t t t pt SKT V cT SKt T S K V c ρ ρ + − = +

Q一流体流经管路损失的热量,W: S,—换热面积,m2: K一从传感器到换热器热水入口管程总传热系数,W1m2.: V—体积流量,m31s: p,一流体密度,gm: Cm—比热,J1gK. 注:S=πd。h K=a1=0.023×子×R×P(流体被加热n=04:流体被冷却n=03) d R.=due L,事 d。—管外径,d。0.032m: -从传感器到换热器热水入口的长度,10.3m: d -管内径,d,=0.025m: 4一流体流速,m/5: 4,—粘度,Pa5: 入,—导热系数,W1mK。 根据T查得流体密度P,、比热cm、粘度4,及导热系数入,代入上面公式进行 计算。严格地讲,应取T和T的平均值,然后查物性数据再进行试算,直至相邻 两次计算出的T相接近为止,但这里不作要求。下面的和计算类似。 计算 2-SaKe(-)-Epcp(G:-T) (10) 2 整理得: T= p3-K6+Sa 2 VPEn-Saka (11) 式中: 2 Q一从换热器热水出口到传感器损失的热量,W: S2—换热面积,m2: K,2一从换热器热水出口到传感器的管程总传热系数,W1m2.K: V—体积流量,m1s:
Q1——流体流经管路损失的热量,W ; t1 S ——换热面积, 2 m ; Kt1——从传感器到换热器热水入口管程总传热系数, 2 Wm K / ⋅ ; Vt ——体积流量, 3 m s/ ; ρ t ——流体密度, 3 kg m/ ; pt c ——比热, J kg K / ⋅ 。 注: t ot 1 1 S dl = π (流体被加热 n=0.4;流体被冷却 n=0.3) , , ; o d ——管外径, o d =0.032m; t1 l ——从传感器到换热器热水入口的长度, t1 l =0.3m; di ——管内径,di =0.025m; t u ——流体流速,m s/ ; μ t ——粘度, Pa s⋅ ; λt ——导热系数,W mK / ⋅ 。 根据T1查得流体密度 ρ t 、比热 pt c 、粘度μ t 及导热系数λt 代入上面公式进行 计算。严格地讲,应取T1和 ' T1 的平均值,然后查物性数据再进行试算,直至相邻 两次计算出的 ' T1 相接近为止,但这里不作要求。下面的 ' T2和 ' 2t 计算类似。 计算 ' T2 (10) 整理得: (11) 式中: Q2——从换热器热水出口到传感器损失的热量,W ; t 2 S ——换热面积, 2 m ; Kt 2 ——从换热器热水出口到传感器的管程总传热系数, 2 Wm K / ⋅ ; Vt ——体积流量, 3 m s/ ; 0.8 1 1 0.023 t n tt er i K RP d λ = = ×× × α pt t r t c P μ λ = it t e t d u R ρ μ = 2 4 t t i V u d π = ' 2 2 ' 2 22 0 2 2 ( ) () 2 t t t t pt T T Q SK t V c T T ρ + = −= − 2 22 2 2 20 ' 2 2 2 2 2 t t t t pt t t t t t t pt SKT V cT SKt T S K V c ρ ρ − + = −

p,—流体密度,gm: C—比热,J/g·K。 注:S2=πd,a K:=a。=0023×子×心×((流体技加热n=04:流体技冷知n=03) 44 d。—管外径,d。0.032m: 2一从换热器热水出口到传感器的长度,20.3m: d,—管内径,d,=0.025m: 4一流体流速,m/s: 4,—粘度,Pas: 元,一导热系数,W/mK。 根据Z,查得流体密度P,、比热c、粘度4,及导热系数元,代入上面公式进行计算 计算 q:=S.Ka(-)=V.p.cm(-b) (12) 整理得: 62= V.p.cml-Sk+Sak 2 SK32 (13) V,P.Cm 式中: 92一从换热器冷水出口到传感器损失的热量,W: S2一换热面积,m2: K一从换热器冷水出口到传感器的管程总传热系数,W1m2,K: ,—体积流量,m/s: p,—流体密度,gm2: C—比热,JkgK。 注:S2=πd2 K:=a,=0.023×子×R×P(流体被加热n=04:流体被冷却n=03) 2,=
ρ t ——流体密度, 3 kg m/ ; pt c ——比热, J kg K / ⋅ 。 注: t ot 2 2 S dl = π (流体被加热 n=0.4;流体被冷却 n=0.3) , , ; o d ——管外径, o d =0.032m; t 2 l ——从换热器热水出口到传感器的长度, t 2 l =0.3m; di ——管内径,di =0.025m; t u ——流体流速,m s/ ; μ t ——粘度, Pa s⋅ ; λt ——导热系数,W mK / ⋅ 。 根据T2 查得流体密度 ρ t 、比热 pt c 、粘度μ t 及导热系数λt 代入上面公式进行计算。 计算 ' 2t (12) 整理得: (13) 式中: 2 q —— 从换热器冷水出口到传感器损失的热量,W ; s2 S ——换热面积, 2 m ; Ks2 ——从换热器冷水出口到传感器的管程总传热系数, 2 Wm K / ⋅ ; Vs ——体积流量, 3 m s/ ; ρs——流体密度, 3 kg m/ ; ps c ——比热, J kg K / ⋅ 。 注: s2 2 o s S dl = π (流体被加热 n=0.4;流体被冷却 n=0.3) is s e s d u R ρ μ = , ps s r s c P μ λ = , 2 4 s s i V u d π = ; 0.8 2 2 0.023 t n t t er i K R P d λ = = ×× × α pt t r t c P μ λ = it t e t d u R ρ μ = 2 4 t t i V u d π = ' 2 2 ' 2 22 0 2 2 ( ) () 2 s s s s ps t t q SK t V c t t ρ + = −= − 2 22 2 2 20 ' 2 2 2 2 2 s s s s ps s s s s s s ps SKt V ct SKt t S K V c ρ ρ − + = − 0.8 2 0.023 s n s s er i K R P d λ = = ×× × α