
过程设备设计 2.2回转薄壳应力分析 2.2回转薄壳应力分析 本章重点 教学重点: (1)回转薄壳的无力矩理论: (2)微元平衡方程、区域平衡方程; (3)回转薄壳的不连续分析。 教学难点: (1)储存液体的圆球壳; (2)圆柱壳受边缘力和边缘力矩作用的弯曲解。 2/74
2.2 回转薄壳应力分析 过程设备设计 2.2 回转薄壳应力分析 教学重点: (1)回转薄壳的无力矩理论 )回转薄壳的无力矩理论; (2)微元平衡方程 )微元平衡方程、区域平衡方程 、区域平衡方程; 本章重点 2 / 74 (3)回转薄壳的不连续分析 )回转薄壳的不连续分析。 教学难点: (1)储存液体的圆球壳 )储存液体的圆球壳; (2)圆柱壳受边缘力和边缘力矩作用的弯曲解 )圆柱壳受边缘力和边缘力矩作用的弯曲解

过程设备设计 2.2回转薄壳应力分析 2.2回转薄壳应力分析 2.2.1薄壁圆筒的应力 2.2.2回转薄壳的无力矩理论 2.2.3无力矩理论的基本方程 2.2.4无力矩理论的应用 2.2.5回转薄壳的不连续分析 3/74
2.2 回转薄壳应力分析 过程设备设计 2.2 回转薄壳应力分析 2.2.1 薄壁圆筒的应力 2.2.2 回转薄壳的无力矩理论 2.2.3 无力矩理论的基本方程 2.2.4 3 / 74 2.2.4 无力矩理论的应用 2.2.5 回转薄壳的不连续分析

过程设备设计 2.2回转薄壳应力分析 2.2回转薄壳应力分析 概念 壳体 以两个曲面为界,且曲面之间的距离远比其它方向 尺寸小得多的构件。 壳体中面 与壳体两个曲面等距离的点所组成的曲面。 薄壳 壳体厚度t与其中面曲率半径R的比值(t/R)max≤1/I0。 外直径与内直径的比值 薄壁圆柱壳或薄壁圆筒 (D,/D)max≤1.1-1.2 厚壁圆柱壳或厚壁圆筒 外直径与内直径的比值 (D,/D)max>1.1-1.2 4/74
2.2 回转薄壳应力分析 过程设备设计 2.2 回转薄壳应力分析 概念 壳体 以两个曲面为界,且曲面之间的距离远比其它方向 ,且曲面之间的距离远比其它方向 尺寸小得多的构件。 壳体中面 与壳体两个曲面等距离的点所组成的曲面。 4 / 74 薄壳 壳体厚度t与其中面曲率半径R的比值(t/R)max≤1/10。 外直径与内直径的比值 (Do/Di)max≤1.1-1.2 薄壁圆柱壳或薄壁圆筒 厚壁圆柱壳或厚壁圆筒 外直径与内直径的比值 (Do/Di)max> 1.1-1.2
过程设备设计 2.2回转薄壳应力分析 2.2回转薄壳应力分析 分析思路 特殊壳体(薄壁圆筒) 般壳体(任意回转薄壳) 特殊壳体(球壳、椭球壳、锥壳) 5/74
2.2 回转薄壳应力分析 过程设备设计 2.2 回转薄壳应力分析 分析思路 特殊壳体(薄壁圆筒) 一般壳体(任意回转薄壳) 5 / 74 一般壳体(任意回转薄壳) 特殊壳体(球壳、椭球壳、锥壳)
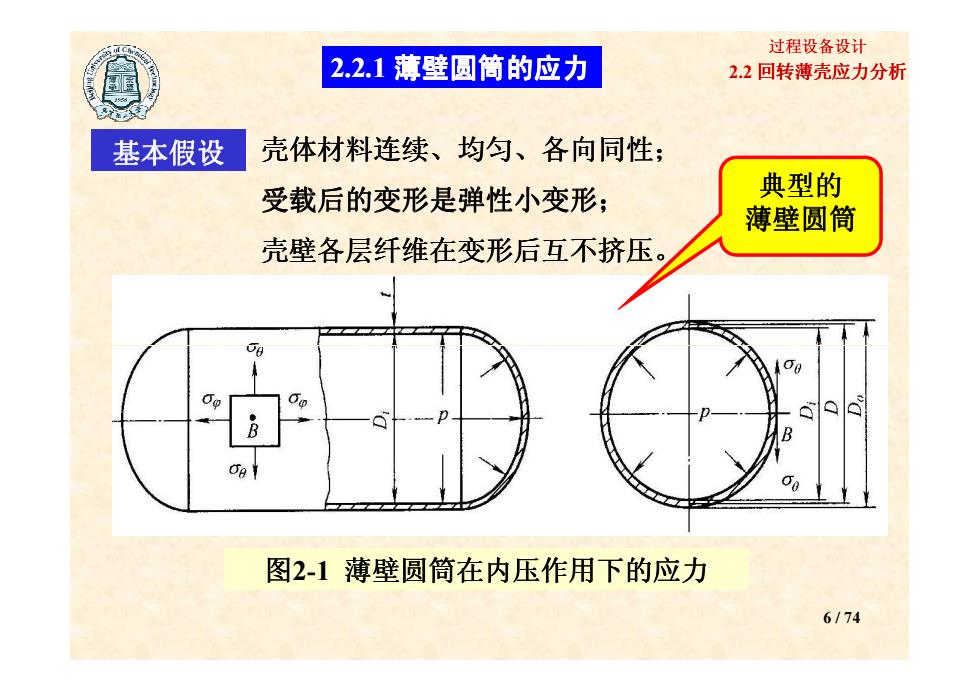
过程设备设计 2.2.1薄壁圆筒的应力 2.2回转薄壳应力分析 基本假设 壳体材料连续、均匀、各向同性: 受载后的变形是弹性小变形: 典型的 薄壁圆筒 壳壁各层纤维在变形后互不挤压。 B 图2-1薄壁圆筒在内压作用下的应力 6/74
2.2 回转薄壳应力分析 过程设备设计 2.2.1 薄壁圆筒的应力 基本假设 壳体材料连续、均匀、各向同性; 受载后的变形是弹性小变形; 壳壁各层纤维在变形后互不挤压。 典型的 薄壁圆筒 6 / 74 图2-1 薄壁圆筒在内压作用下的应力
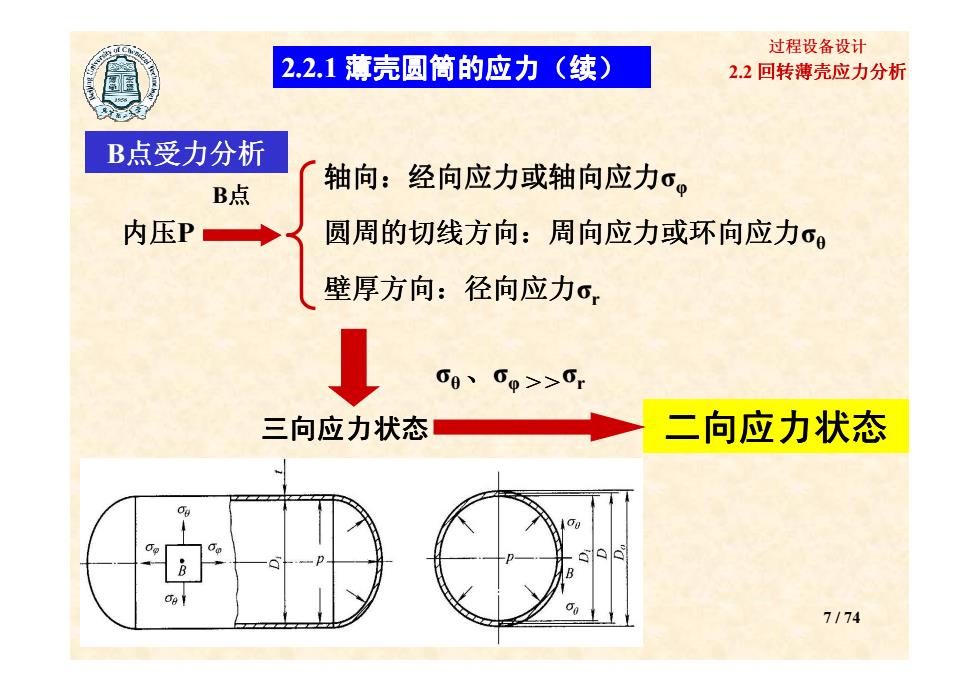
过程设备设计 2.2.1薄壳圆筒的应力(续) 2.2回转薄壳应力分析 B点受力分析 B点 轴向:经向应力或轴向应力σ。 内压P 圆周的切线方向:周向应力或环向应力σ 壁厚方向:径向应力σ 00、0φ>>0 三向应力状态 二向应力状态 7/74
2.2 回转薄壳应力分析 过程设备设计 2.2.1 薄壳圆筒的应力 薄壳圆筒的应力 薄壳圆筒的应力 薄壳圆筒的应力(续) B点受力分析 内压P B点 轴向:经向应力或轴向应力 :经向应力或轴向应力σφ 圆周的切线方向:周向应力或环向应力 :周向应力或环向应力σθ 壁厚方向:径向应力σr 7 / 74 三向应力状态 二向应力状态 σθ 、σφ >>σr
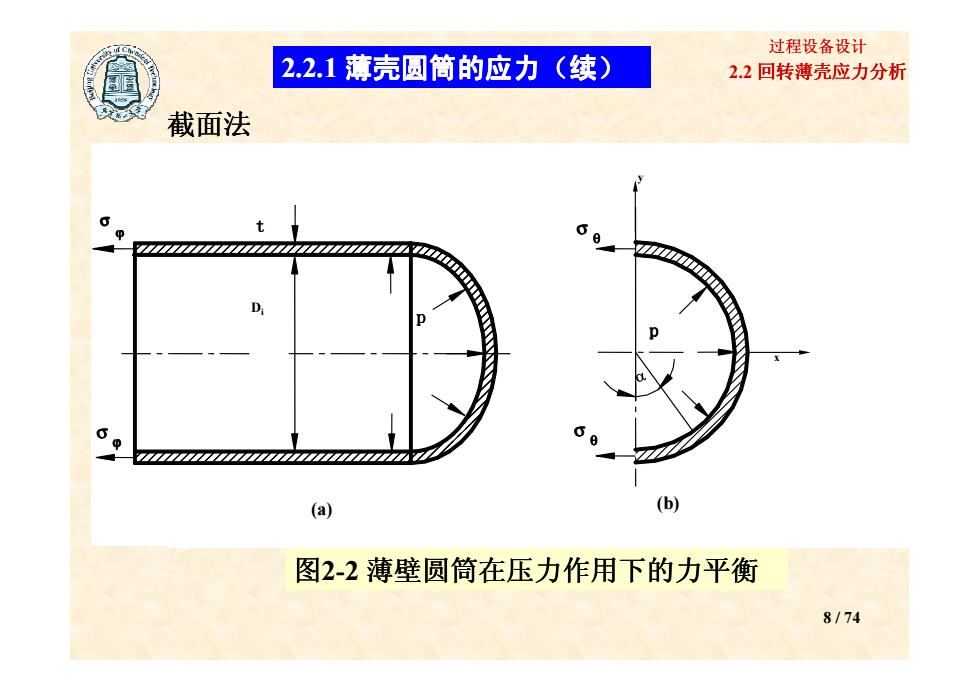
过程设备设计 2.2.1薄壳圆筒的应力(续) 2.2回转薄壳应力分析 截面法 D (a) (b) 图2-2薄壁圆筒在压力作用下的力平衡 8/74
2.2 回转薄壳应力分析 过程设备设计 截面法 σ ϕ σ θ p p y Di t 2.2.1 薄壳圆筒的应力 薄壳圆筒的应力 薄壳圆筒的应力 薄壳圆筒的应力(续) 8 / 74 σ ϕ σ θ (a) (b) x 图2-2 薄壁圆筒在压力作用下的力平衡

过程设备设计 2.2.1薄壳圆筒的应力(续) 2.2回转薄壳应力分析 轴向平衡 元Dp=Dton→0o= 4t 应力 静定 求解 图2-2 周向平衡 PpR,sinoa=2io。→0g= 2t 09=200 9/74 图2-2薄壁圆筒在压力作用下的力平衡
2.2 回转薄壳应力分析 过程设备设计 应力 求解 周向平衡 静定 图2-2 轴向平衡 θ π 2 2 pRi sinαdα 2tσ 0 = ∫ D p2 4π = πDtσ ϕ t pD 2 σ θ = σ ϕ t pD4 = 2.2.1 薄壳圆筒的应力 薄壳圆筒的应力 薄壳圆筒的应力 薄壳圆筒的应力(续) 9 / 74 周向平衡 α α σ θ pR d t i 2 sin 2 0 = ∫ 2t θ σ θ σ ϕ σ ϕ = 2 σ ϕ σ θ σ θ p p α (a) (b) y x Di t σ ϕ σ ϕ σ θ σ θ p p α σ ϕ σ ϕ σ θ σ θ p p α (a) (b) y x Di t 图2-2 薄壁圆筒在压力作用下的力平衡

过程设备设计 2.2回转薄壳应力分析 2.2回转薄壳应力分析 2.2.1薄壁圆筒的应力 2.2.2回转薄壳的无力矩理论 2.2.3无力矩理论的基本方程 2.2.4无力矩理论的应用 2.2.5回转薄壳的不连续分析 10/74
2.2 回转薄壳应力分析 过程设备设计 2.2 回转薄壳应力分析 2.2.1 薄壁圆筒的应力 2.2.2 回转薄壳的无力矩理论 2.2.3 无力矩理论的基本方程 2.2.4 10 / 74 2.2.4 无力矩理论的应用 2.2.5 回转薄壳的不连续分析
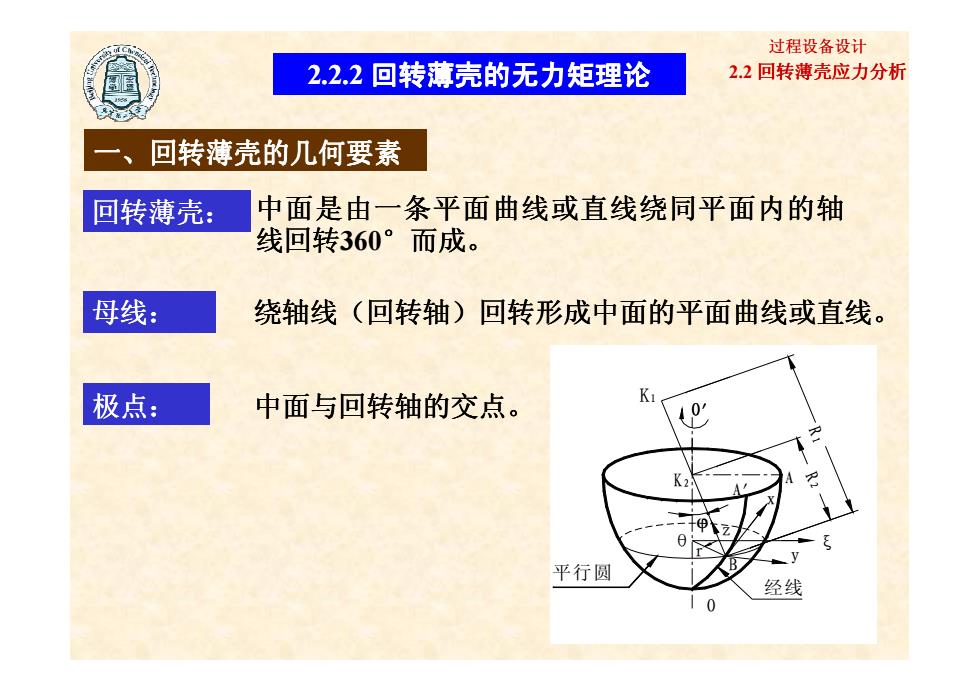
过程设备设计 2.2.2回转薄壳的无力矩理论 2.2回转薄壳应力分析 回转薄壳的几何要素 回转薄壳: 中面是由一条平面曲线或直线绕同平面内的轴 线回转360°而成。 母线: 绕轴线(回转轴)回转形成中面的平面曲线或直线。 极点: 中面与回转轴的交点。 K 0 平行圆 经线 0
2.2 回转薄壳应力分析 过程设备设计 2.2.2 回转薄壳的无力矩理论 一、回转薄壳的几何要素 、回转薄壳的几何要素 回转薄壳的几何要素 回转薄壳的几何要素 回转薄壳: 中面是由一条平面曲线或直线绕同平面内的轴 线回转360°而成。 母线: 绕轴线(回转轴)回转形成中面的平面曲线或直线 )回转形成中面的平面曲线或直线。 11 / 74 极点: 中面与回转轴的交点。 θ A' A x z r y a. R R O' K1 K2 平行圆 经线 ξ O' O ϕ B 1 2 θ A' A x z r y a. R R O' K1 K2 平行圆 经线 ξ O' O ϕ B 1 2