
过程设备设计 2.3厚壁圆筒应力分析 2.3厚壁圆简应力分析 教学重点: (1)厚壁圆筒中三向应力的公式表达 和应力分布图; (2)厚壁圆筒中的弹塑性区的应力分布; (3)提高屈服承载能力的措施。 教学难点: 厚壁圆简中三向应力公式推导。 2/52
2.3 厚壁圆筒应力分析 过程设备设计 教学重点: (1)厚壁圆筒中三向应力的公式表达 )厚壁圆筒中三向应力的公式表达 和应力分布图; (2)厚壁圆筒中的弹塑性区的应力分布; 2.3 厚壁圆筒应力分析 2 / 52 (2)厚壁圆筒中的弹塑性区的应力分布; (3)提高屈服承载能力的措施 )提高屈服承载能力的措施。 教学难点: 厚壁圆筒中三向应力公式推导

过程设备设计 主要内容 2.3厚壁圆筒应力分析 2.3.1弹性应力 2.3.2弹塑性应力 2.3.3屈服压力和爆破压力 2.3.4提高屈服承载能力的措施 3/52
2.3 厚壁圆筒应力分析 过程设备设计 2.3.1 弹性应力 2.3.2 弹塑性应力 主要内容 3 / 52 2.3.3 屈服压力和爆破压力 2.3.4 提高屈服承载能力的措施

过程设备设计 2.3厚壁圆筒应力分析 厚壁容器: D。/D,>1.1-12 应考虑径向应力,是三向应力状态; 应力特征: 应力沿壁厚不均匀分布; 若内外壁间的温差大,应考虑器壁中的热应力。 静不定问题,需平衡、几何、物理等方程 分析方法: 联立求解 厚壁圆简分单层式和组合式两种,本书将只分析单层厚 壁圆筒的弹性应力、弹塑性应力、屈服应力和爆破压力。 4/52
2.3 厚壁圆筒应力分析 过程设备设计 厚壁容器: D o / D i > 1.1 − 2.1 应力特征: 应考虑径向应力,是三向应力状态 ,是三向应力状态; 应力沿壁厚不均匀分布; 若内外壁间的温差大,应考虑器壁中的热应力 ,应考虑器壁中的热应力。 应考虑径向应力,是三向应力状态 ,是三向应力状态; 应力沿壁厚不均匀分布; 若内外壁间的温差大,应考虑器壁中的热应力 ,应考虑器壁中的热应力。 4 / 52 分析方法: 静不定问题,需平衡、几何、物理等方程 联立求解 静不定问题,需平衡、几何、物理等方程 联立求解 厚壁圆筒分单层式和组合式两种,本书将只分析单层厚 ,本书将只分析单层厚 壁圆筒的弹性应力、弹塑性应力、屈服应力和爆破压力 、屈服应力和爆破压力
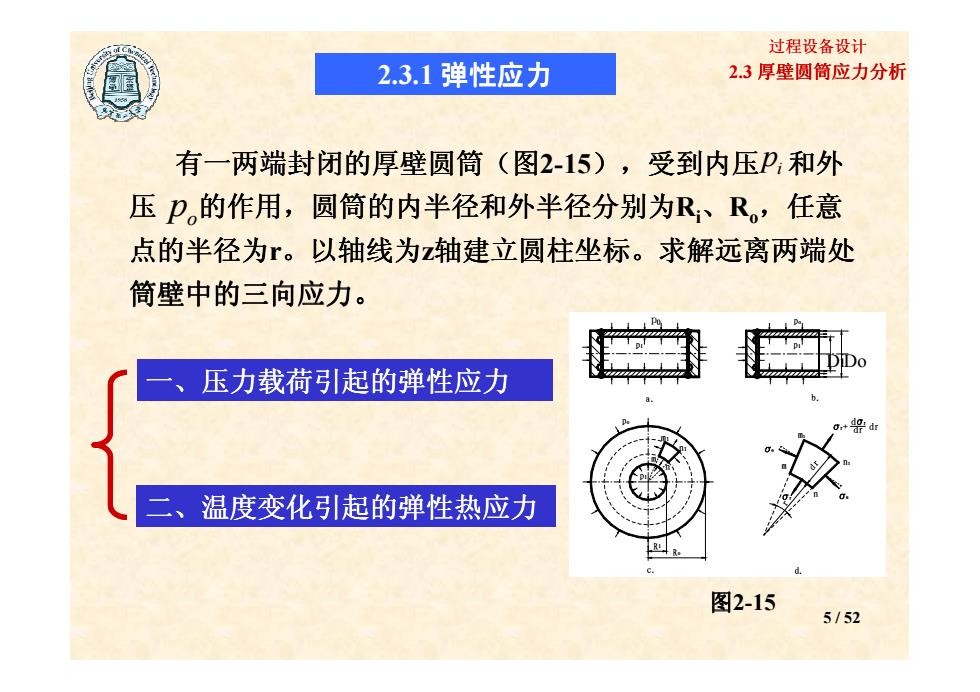
过程设备设计 2.3.1弹性应力 2.3厚壁圆筒应力分析 有一两端封闭的厚壁圆筒(图2-15),受到内压P,和外 压卫的作用,圆筒的内半径和外半径分别为R、R。,任意 点的半径为。以轴线为z轴建立圆柱坐标。求解远离两端处 筒壁中的三向应力。 一、 压力载荷引起的弹性应力 二、温度变化引起的弹性热应力 图2-15 5/52
2.3 厚壁圆筒应力分析 过程设备设计 2.3.1 弹性应力 有一两端封闭的厚壁圆筒(图2-15),受到内压 和外 压 的作用,圆筒的内半径和外半径分别为 ,圆筒的内半径和外半径分别为Ri、Ro,任意 点的半径为r。以轴线为z轴建立圆柱坐标。求解远离两端处 。求解远离两端处 筒壁中的三向应力。 i p o p pi po pi p0 5 / 52 一、压力载荷引起的弹性应力 、压力载荷引起的弹性应力 压力载荷引起的弹性应力 压力载荷引起的弹性应力 二、温度变化引起的弹性热应力 、温度变化引起的弹性热应力 温度变化引起的弹性热应力 温度变化引起的弹性热应力 b. c. d. pi a. po pi m n m1 n1 Ri Ro m1 n1 m r n θ θ r+ d r dr dr r dr pi DiDo 图2-15
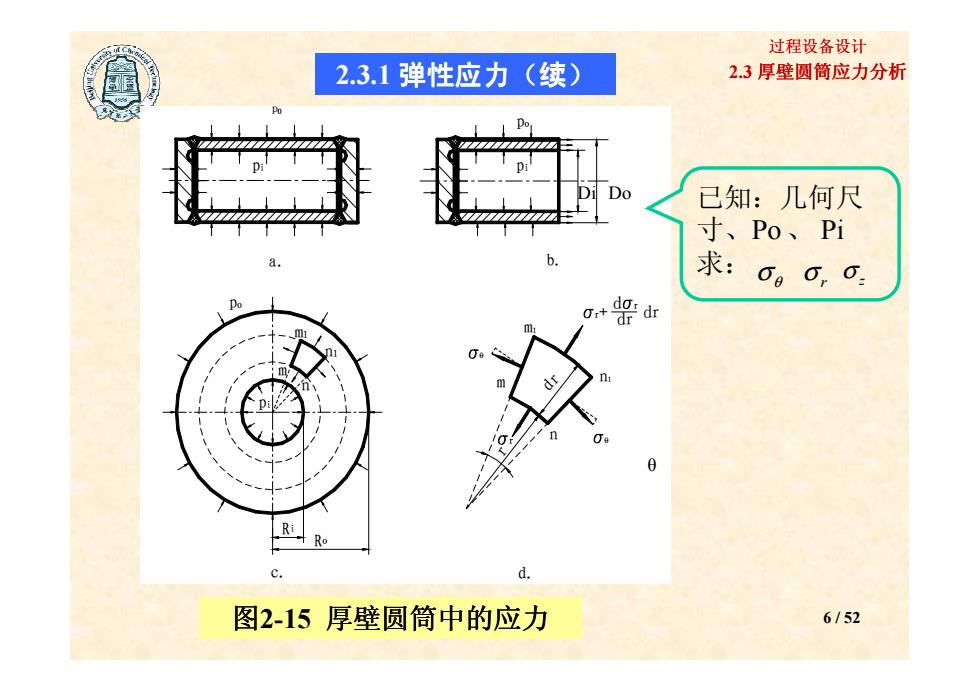
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 Di Do 已知:几何尺 寸、Po、Pi 求: 0.0,0 do, dr dr RR阳 图2-15厚壁圆筒中的应力 6/52
2.3 厚壁圆筒应力分析 过程设备设计 b. pi a. po m1 n m1 r+ d r dr dr po pi p0 Di Do 2.3.1 弹性应力(续) 已知:几何尺 寸、Po、 Pi 求:σθ σ r σ z 图2-15 厚壁圆筒中的应力 6 / 52 c. d. pi m n n1 Ri Ro n1 m r n θ θ r dr θ
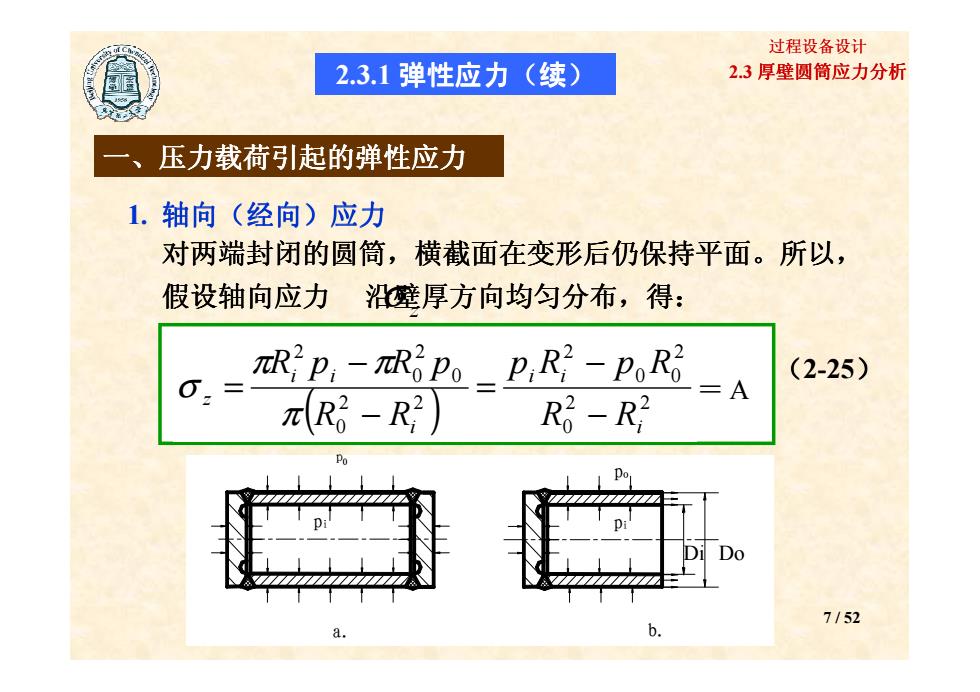
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 一、压力载荷引起的弹性应力 1.轴向(经向)应力 对两端封闭的圆筒,横截面在变形后仍保持平面。所以, 假设轴向应力沿壁厚方向均匀分布,得: πRp,-Rpo-p,R-pR6 (2-25) -A πR-R2) Ro-R2 Po Do 7152
2.3 厚壁圆筒应力分析 过程设备设计 一、压力载荷引起的弹性应力 、压力载荷引起的弹性应力 、压力载荷引起的弹性应力 、压力载荷引起的弹性应力 压力载荷引起的弹性应力 压力载荷引起的弹性应力 压力载荷引起的弹性应力 压力载荷引起的弹性应力 1. 轴向(经向)应力 2 2 2 2 πR p − πR p p R − p R 对两端封闭的圆筒,横截面在变形后仍保持平面 ,横截面在变形后仍保持平面。所以, 假设轴向应力 沿壁厚方向均匀分布 σ z ,得: 2.3.1 弹性应力(续) 7 / 52 ( ) 2 2 0 2 0 0 2 2 2 0 0 2 0 2 i i i i i i z R R p R p R R R R p R p −− = −− = π π π σ (2-25) = A b. pi a. po pi p0 Di Do b. pi a. po pi p0 b. pi a. po pi p0 Di Do

过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆简应力分析 2.周向应力与径向应力 由于应力分布的不均匀性,进行应力分析时,必须从微元体着 手,分析其应力和变形及它们之间的相互关系。 a.微元体 b.平衡方程 c.几何方程:微元体位移与应变之间的关系(用位移法求解) d.物理方程:弹性范围内,微元体的应变与应力的关系 .平衡、几何和物理方程综合一求解应力的微分方程 (求解微分方程,积分,边界条件定常数) 应力 8/52
2.3 厚壁圆筒应力分析 过程设备设计 2. 周向应力与径向应力 由于应力分布的不均匀性,进行应力分析时 ,进行应力分析时,必须从微元体着 ,必须从微元体着 手,分析其应力和变形及它们之间的相互关系 分析其应力和变形及它们之间的相互关系。 a. 微元体 b. 平衡方程 c. 几何方程 :微元体位移与应变之间的关系(用位移法求解) 2.3.1 弹性应力(续) 8 / 52 c. 几何方程 :微元体位移与应变之间的关系(用位移法求解) d. 物理方程:弹性范围内,微元体的应变与应力的关系 ,微元体的应变与应力的关系 e. 平衡、几何和物理方程综合 、几何和物理方程综合—求解应力的微分方程 (求解微分方程 (求解微分方程,积分,边界条件定常数 ,边界条件定常数) 应 力
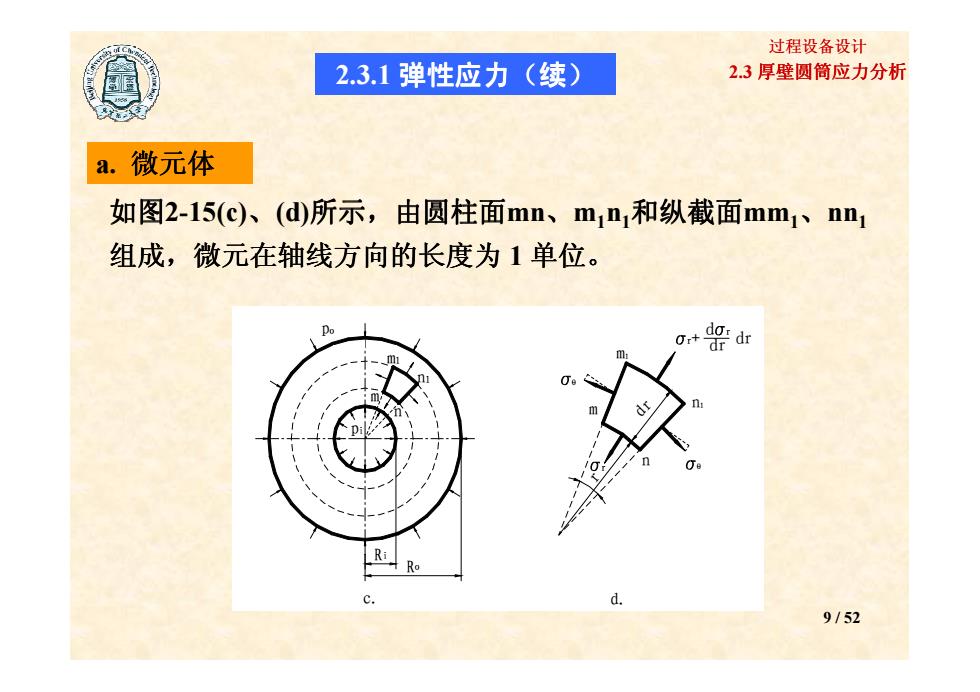
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 a. 微元体 如图2-15(c)、(d)所示,由圆柱面mn、m11和纵截面mm1、nn1 组成,微元在轴线方向的长度为1单位。 Or+ do:dr dr d. 9152
2.3 厚壁圆筒应力分析 过程设备设计 a. 微元体 如图2-15(c)、(d)所示,由圆柱面mn、m1n1和纵截面mm1、nn1 组成,微元在轴线方向的长度为 ,微元在轴线方向的长度为 1 单位。 2.3.1 弹性应力(续) po m r+ d r dr dr po m r+ d r dr dr po m r+ d r dr dr 9 / 52 c. d. pi m n m1 n1 Ri Ro m1 n1 m r n θ θ + dr dr r dr c. d. pi m n m1 n1 Ri Ro m1 n1 m r n θ θ + dr dr r dr c. d. pi m n m1 n1 Ri Ro m1 n1 m r n θ θ + dr dr r dr
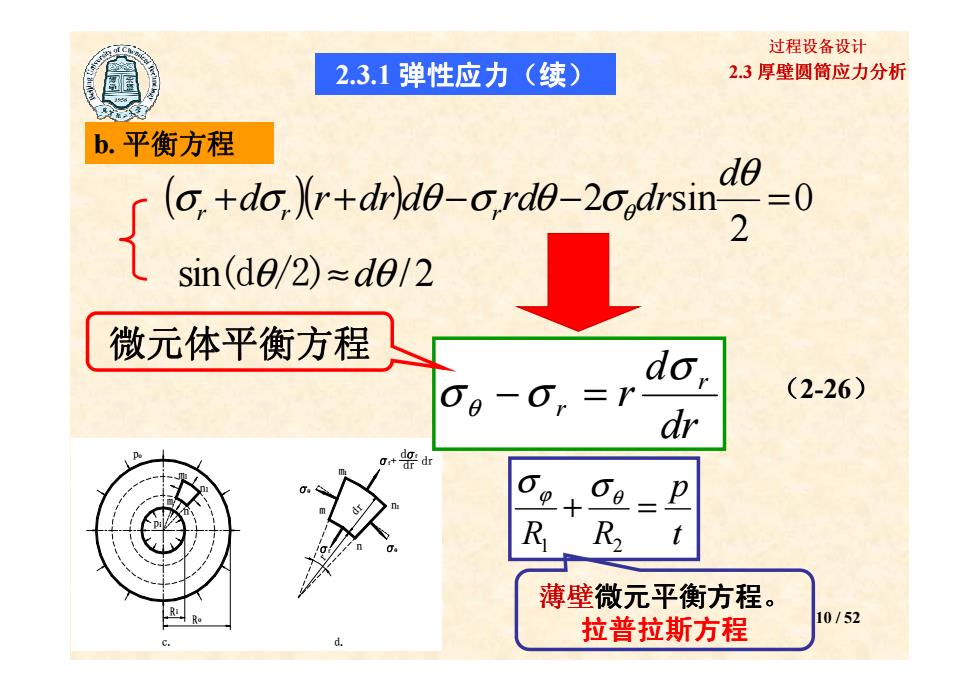
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 b.平衡方程 de de.dro-ordo-20drin sin(d0/2)≈dg/2 微元体平衡方程 do (2-26) dr 6 R R2 薄壁微元平衡方程。 拉普拉斯方程 10/52
2.3 厚壁圆筒应力分析 过程设备设计 b. 平衡方程 2.3.1 弹性应力(续) ( )( ) 0 2 + + − −2 sin = θ σ σ θ σ θ σθ d d r dr d rd dr r r r sin /2 (d /2) θ θ ≈d dσ 微元体平衡方程 10 / 52 t p R R + = 1 2 ϕ σ θ σ c. d. po pi m n m1 n1 Ri Ro m1 n1 m n r θ θ r+ d r dr dr r dr c. d. po pi m n m1 n1 Ri Ro m1 n1 m n r θ θ r+ d r dr dr r dr c. d. po pi m n m1 n1 Ri Ro m1 n1 m n r θ θ r+ d r dr dr r dr dr d r r r σ σ θ −σ = (2-26) 微元体平衡方程 薄壁微元平衡方程。 拉普拉斯方程
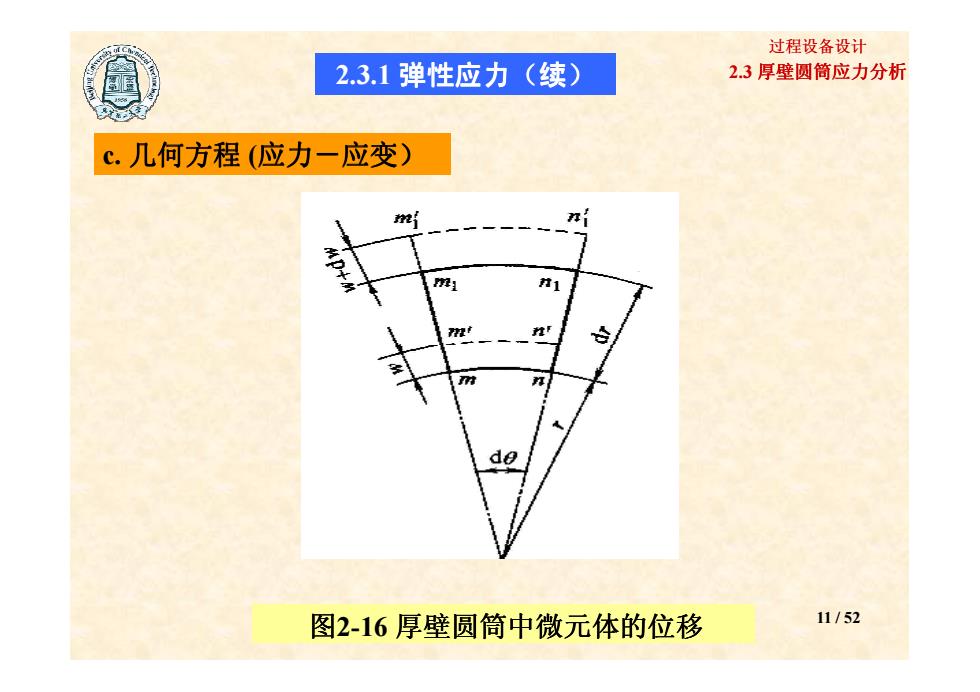
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 c.几何方程(应力一应变) de 图2-16厚壁圆筒中微元体的位移 11/52
2.3 厚壁圆筒应力分析 过程设备设计 c. 几何方程 (应力-应变) 2.3.1 弹性应力(续) 图 11 / 52 2-16 厚壁圆筒中微元体的位移