
第10卷第2期 智能系统学报 Vol.10 No.2 2015年4月 CAAI Transactions on Intelligent Systems Apr.2015 D0:10.3969/j.issn.1673-4785.201312036 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20150302.1105.001.html 一种带有属性偏好的模糊多属性决策方法 吕智颖2,黄天民,梁学章 (1.西南交通大学数学学院,四川成都610031:2.齐齐哈尔大学理学院,黑龙江齐齐哈尔161006:3.吉林大学数 学学院,吉林长春130012) 摘要:结合投资决策的特点给出了一种模糊多属性决策方法,其中属性偏好信息以若干个互补判断矩阵形式给 出,属性值为梯形模糊数。该方法能充分挖掘判断矩阵的特征信息,给出了互补判断矩阵相似度和属性优势度的定 义,从而确定专家权重和属性权重。基于梯形模糊数外接圆的圆心与原点之间所形成的矩形面积来对模糊数排序 的方法对方案进行排序和择优。通过对服务行业的项目评估问题说明该方法是求解模糊多属性决策问题的一种有 效的工具,并且操作简便、易于在计算机上实现。 关键词:多属性决策;梯形模糊数;互补判断矩阵:相似接近度:优先度指数;投资决策 中图分类号:TP18:0159文献标志码:A文章编号:1673-4785(2015)02-0227-07 中文引用格式:吕智颗,黄天民,梁学章.一种带有属性偏好的模糊多属性决策方法[J].智能系统学报,2015,10(2):227-233. 英文引用格式:Lyu Zhiying,HUANG Tianmin,LIANG Xuezhang.A method for fuzz四y multi-attribute decision-making with prefer- ence to attribute[J].CAAI Transactions on Intelligent Systems,2015,10(2):227-233. A method for fuzzy multi-attribute decision-making with preference to attribute LYU Zhiying'2,HUANG Tianmin',LIANG Xuezhang3 (1.College of Mathematics,Southwest Jiaotong University,Chengdu 610031,China;2.Department of Mathematics,Qiqihar Univer- sity,Qiqihar 161006,China;3.College of Mathematics,Jilin University,Changchun 130012,China) Abstract:In this paper,a method for fuzzy multi-attribute decision-making problem considering the characteristics of investment decisions is investigated.The preference information about attribute weights given by the decision makers is in the form of complementary judgment matrixes and the attribute value in the decision matrix is trape- zoidal fuzzy number.The attribute weight and expert vectors are received by exploring the feather information of judgment matrixes given by experts about attribute.A new method for ranking alternatives by using ranking trape- zoidal fuzzy number based on the area between circumcenter of centroids of a fuzzy number and origin is proposed. Finally,a project evaluation problem for services showed that the proposed method is an effective tool to solve the fuzzy multi-attribute decision-making problems,featuring by simple operations and easy implementation on a com- puter. Keywords:multi-attribute decision making;trapezoidal fuzzy number;complementary judgment matrix;similar approach degree;superiority index;investment decision 在多属性决策中,往往需要对方案或属性进行 两两比较,形成判断矩阵。在实际的决策过程中,专 家受到知识结构、评判水平和个人偏好等众多因素 收稿日期:2014-04-01.网络出版日期:2015-0302. 的影响所给出的判断矩阵是不同的,因此需要集结 基金项目:国家自然科学基金资助项目(11271041):中央高校科研业 务费专项资金资助项目(swj如11ZT29). 多个专家给出的判断矩阵进行决策。根据判断矩阵 通信作者:吕智颖.E-mail:lvzhiying1979@163.com
第 10 卷第 2 期 智 能 系 统 学 报 Vol.10 №.2 2015 年 4 月 CAAI Transactions on Intelligent Systems Apr. 2015 DOI:10.3969 / j.issn.1673⁃4785.201312036 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20150302.1105.001.html 一种带有属性偏好的模糊多属性决策方法 吕智颖1,2 , 黄天民1 ,梁学章3 (1.西南交通大学 数学学院,四川 成都 610031; 2. 齐齐哈尔大学 理学院,黑龙江 齐齐哈尔 161006; 3. 吉林大学 数 学学院,吉林 长春 130012) 摘 要:结合投资决策的特点给出了一种模糊多属性决策方法, 其中属性偏好信息以若干个互补判断矩阵形式给 出,属性值为梯形模糊数。 该方法能充分挖掘判断矩阵的特征信息,给出了互补判断矩阵相似度和属性优势度的定 义,从而确定专家权重和属性权重。 基于梯形模糊数外接圆的圆心与原点之间所形成的矩形面积来对模糊数排序 的方法对方案进行排序和择优。 通过对服务行业的项目评估问题说明该方法是求解模糊多属性决策问题的一种有 效的工具,并且操作简便、易于在计算机上实现。 关键词:多属性决策;梯形模糊数;互补判断矩阵;相似接近度;优先度指数; 投资决策 中图分类号: TP18;O159 文献标志码:A 文章编号:1673⁃4785(2015)02⁃0227⁃07 中文引用格式:吕智颖,黄天民,梁学章. 一种带有属性偏好的模糊多属性决策方法[J]. 智能系统学报, 2015, 10(2): 227⁃233. 英文引用格式:Lyu Zhiying, HUANG Tianmin,LIANG Xuezhang. A method for fuzzy multi⁃attribute decision⁃making with prefer⁃ ence to attribute[J]. CAAI Transactions on Intelligent Systems, 2015, 10(2): 227⁃233. A method for fuzzy multi⁃attribute decision⁃making with preference to attribute LYU Zhiying 1,2 , HUANG Tianmin 1 , LIANG Xuezhang 3 (1. College of Mathematics, Southwest Jiaotong University, Chengdu 610031, China; 2. Department of Mathematics, Qiqihar Univer⁃ sity, Qiqihar 161006, China; 3.College of Mathematics, Jilin University, Changchun 130012, China) Abstract:In this paper, a method for fuzzy multi⁃attribute decision⁃making problem considering the characteristics of investment decisions is investigated. The preference information about attribute weights given by the decision makers is in the form of complementary judgment matrixes and the attribute value in the decision matrix is trape⁃ zoidal fuzzy number. The attribute weight and expert vectors are received by exploring the feather information of judgment matrixes given by experts about attribute. A new method for ranking alternatives by using ranking trape⁃ zoidal fuzzy number based on the area between circumcenter of centroids of a fuzzy number and origin is proposed. Finally, a project evaluation problem for services showed that the proposed method is an effective tool to solve the fuzzy multi⁃attribute decision⁃making problems,featuring by simple operations and easy implementation on a com⁃ puter. Keywords: multi⁃attribute decision making; trapezoidal fuzzy number; complementary judgment matrix; similar approach degree; superiority index; investment decision 收稿日期:2014⁃04⁃01. 网络出版日期:2015⁃03⁃02. 基金项目:国家自然科学基金资助项目(11271041); 中央高校科研业 务费专项资金资助项目(swjtu11ZT29). 通信作者:吕智颖. E⁃mail: lvzhiying1979@ 163.com. 在多属性决策中,往往需要对方案或属性进行 两两比较,形成判断矩阵。 在实际的决策过程中,专 家受到知识结构、评判水平和个人偏好等众多因素 的影响所给出的判断矩阵是不同的,因此需要集结 多个专家给出的判断矩阵进行决策。 根据判断矩阵

.228 智能系统学报 第10卷 确定各属性的权重和专家权重的方法在多属性决策 为:1)专家赋权:2)属性赋权。这2个步骤均基于 中得到了广泛应用13】。在对多属性决策问题进行 专家给出的判断矩阵,认为判断矩阵中蕴含了反映 分析时,由于客观事物的复杂性和不确定性,人类思 属性权重和专家权重的全部信息。 维的模糊性以及非人为所能控制的估计不精或测量 首先给出关于属性集C的互补判断矩阵定义。 误差等原因,此时采用模糊数来表示决策中出现的 定义1称矩阵P。=(p)mxm为互补判断矩阵, 不确定信息较为贴切。对模糊数排序[4]问题的研 如果对i∈M,p=0.5且对HiJ∈M,P+ 究已经受到了国内外学者的广泛关注,并取得了丰 P=1,其中0≤p≤1表示专家e认为属性c,对属 富的研究成果。梯形模糊数比三角模糊数的隶属函 性c的相对重要程度,c,S∈C。 数更加复杂,并且将区间数或三角模糊数作为特例, 由互补判断矩阵的定义知: 因此可以更好地反映属性值的不确定性。目前以梯 1)若p>0.5,则专家e.认为属性c:优于属性 形模糊数来表示决策信息的多属性决策方法的研究 引起了人们的重视,并取得了一定的研究成果s0。 9,记为c>g: 2)若0≤pc>c>c的情形,称 数的排序方法对方案进行排序和择优。 这种现象为循环现象,其中i,j,l∈M。若集合C的 元素间的优劣关系具有传递性且不存在循环现象, 1 模糊多属性决策方法 称关于C的互补判断矩阵P:具有可接受一致性。 对带有属性偏好的模糊多属性决策问题基本模 通过定义1可以得出每个专家对属性集的排 型可以描述成: 序,根据定义2可以判断P:是否具有可接受一致 决策问题的备选方案集为A={A1,A2,…,An}, 性,如果不具有可接受一致性,应根据一些办法进行 评价方案的属性集为C={c1,c2,…,c},梯形模糊 相应的调整3],使其具有一致性。 数规范化[9]决策矩阵可表示为F=(f)xm,其中 为了得到属性的优劣排序,给出如下定义。 定义3对于专家ek(k∈T),c,C∈C,记 梯形模糊数f,=(a,b,c,d)为方案A:在属性c 下的属性值,属性权重向量为ω= 1,c>g [ω1w2… 1,∑,=1。决定属性偏好的 =0.5,6=c i=l 0. 其他 专家集为E={e1,e2,…,e,},专家的权重向量为 称= ∑专为c优于G的优先度指数,R,= 入=[入1A2… 入,],∑入,=1,专家e:针对属 性集C给出的偏好信息为互补判断矩阵P= 为c(ieM))在C中的优先度 (P)mxm。假设N=1,2,…,n,M={1,2,…,m}, 为了得到属性的优劣排序,给出如下定义。 T={1,2,…,t},决策的目的是找出最优方案或对 定义4对Hc:,c∈C,e∈E,2个属性间不 方案进行优劣排序。 同的序关系可定义为 1.1权重的确定 1)c:≥c当且仅当对Hk∈T,有c≥c且存 基于判断矩阵信息得到属性权重的方法主要分 在ko∈T满足c>c;
确定各属性的权重和专家权重的方法在多属性决策 中得到了广泛应用[ 1⁃3 ] 。 在对多属性决策问题进行 分析时,由于客观事物的复杂性和不确定性,人类思 维的模糊性以及非人为所能控制的估计不精或测量 误差等原因,此时采用模糊数来表示决策中出现的 不确定信息较为贴切。 对模糊数排序[4⁃7] 问题的研 究已经受到了国内外学者的广泛关注,并取得了丰 富的研究成果。 梯形模糊数比三角模糊数的隶属函 数更加复杂,并且将区间数或三角模糊数作为特例, 因此可以更好地反映属性值的不确定性。 目前以梯 形模糊数来表示决策信息的多属性决策方法的研究 引起了人们的重视,并取得了一定的研究成果[8⁃10] 。 目前对于模糊多属性决策问题的研究主要集中 在属性权重的确定和模糊决策矩阵的排序问题上。 本文在以上研究的基础上,研究一种属性值为梯形 模糊数、属性偏好以互补判断矩阵形式给出的不确 定模糊多属性决策[11 ⁃12 ] 问题。 集结专家们给出的 关于属性两两比较的结果以形成群的偏好,给出了 判断矩阵相似接近度和属性优势度的定义,进而确 定专家权重和属性权重。 基于加权平均法对规范化 的模糊属性值进行集结,根据文献[4]给出的模糊 数的排序方法对方案进行排序和择优。 1 模糊多属性决策方法 对带有属性偏好的模糊多属性决策问题基本模 型可以描述成: 决策问题的备选方案集为 A = {A1 ,A2 ,…,An }, 评价方案的属性集为 C = {c1 ,c2 ,…,cm }, 梯形模糊 数规范化[ 9 ]决策矩阵可表示为 F = ( f ~ ij)n×m , 其中 梯形模糊数 f ~ ij = (aij,bij,cij,dij) 为方案 Ai 在属性 cj 下 的 属 性 值, 属 性 权 重 向 量 为 ω = [ω1 ω2 … ω m ], ∑ m i = 1 ωi = 1。 决定属性偏好的 专家集为 E = {e1 ,e2 ,…,et}, 专家的权重向量为 λ =[λ1 λ2 … λt], ∑ t i = 1 λi = 1, 专家 ek 针对属 性集 C 给 出 的 偏 好 信 息 为 互 补 判 断 矩 阵 Pk = (p k ij) m×m 。 假设 N = {1,2,…,n}, M = {1,2,…,m}, T = {1,2,…,t}, 决策的目的是找出最优方案或对 方案进行优劣排序。 1.1 权重的确定 基于判断矩阵信息得到属性权重的方法主要分 为:1)专家赋权;2)属性赋权。 这 2 个步骤均基于 专家给出的判断矩阵,认为判断矩阵中蕴含了反映 属性权重和专家权重的全部信息。 首先给出关于属性集 C 的互补判断矩阵定义。 定义 1 称矩阵 Pk = (p k ij) m×m 为互补判断矩阵, 如果对 ∀i ∈ M, p k ii = 0.5 且对 ∀i,j ∈ M, p k ij + p k ji =1, 其中 0 ≤p k ij ≤1 表示专家 ek 认为属性 ci 对属 性 cj 的相对重要程度, ci,cj ∈ C 。 由互补判断矩阵的定义知: 1)若 p k ij > 0.5, 则专家 ek 认为属性 ci 优于属性 cj, 记为 c k i > c k j ; 2)若 0 ≤ p k ij < 0.5, 则专家 ek 认为属性 ci 劣于 属性 cj, 记为 c k i < c k j ; 3)若 p k ij = 0.5, 则专家 ek 认为属性 ci 与属性 cj 同样重要,记为 c k i = c k j 。 在应用判断矩阵进行决策的过程中,要求判断 矩阵具有较好的一致性,现给出互补判断矩阵可接 受一致性的定义。 定义 2 若在专家 ek 给出的关于属性集合 C 的比较结果中出现形如 c k i > c k j > c k l > c k i 的情形,称 这种现象为循环现象,其中 i,j,l ∈ M 。 若集合 C 的 元素间的优劣关系具有传递性且不存在循环现象, 称关于 C 的互补判断矩阵 Pk 具有可接受一致性。 通过定义 1 可以得出每个专家对属性集的排 序,根据定义 2 可以判断 Pk 是否具有可接受一致 性,如果不具有可接受一致性,应根据一些办法进行 相应的调整[1 3 ] ,使其具有一致性。 为了得到属性的优劣排序,给出如下定义。 定义 3 对于专家 ek (k ∈ T), ci,cj ∈ C, 记 r k ij = 1, c k i > c k j 0.5, c k i = c k j 0, 其他 ì î í ï ï ï ï 称 rij = ∑ t k = 1 r k ij 为 ci 优于 cj 的优先度指数, Ri = ∑ m j = 1 rij 为 ci(i ∈ M) 在 C 中的优先度指数。 为了得到属性的优劣排序,给出如下定义。 定义 4 对 ∀ci,cj ∈ C, ek ∈ E, 2 个属性间不 同的序关系可定义为 1) ci ≥ cj 当且仅当对 ∀k ∈ T, 有 c k i ≥ c k j 且存 在 k0 ∈ T 满足 c k0 i > c k0 j ; ·228· 智 能 系 统 学 报 第 10 卷

第2期 吕智颖,等:一种带有属性偏好的模糊多属性决策方法 ·229. 2)c:>g,当且仅当对k∈T都有c>G。 由于IR4-R。I>t-1,有:当R>R。时, 定义5设c,为C中的一个属性,则有: R'a>R'g;当Rt-1,则ca 式中:sn=s(P。,P),如果u=v,则有sm=1。专家 和c。的序关系在C'=C\c。中是不变的。 e。的平均相似接近度为 证明因为R,=xR,由引理1中3)知c,为 C中的一个非劣属性。 Ae) (2) 现证明对j∈M,均有。≤t-1。假设不成 通过A(en)来确定专家e.的权重为 立,则存在c。∈C,使得rw=1或者w=t-1/2。因 A(e.) 此对VkE7,都有么≥)且存在,∈T使得 入.= (3) ∑A(e) = 如=1。从而对k∈T,都有c≤统且存在k。∈ 设P:=(p)mm(keT)为专家e给出的关于 T,使得c<c0成立。故由定义4,有c,≤c0。再 属性集C的互补判断矩阵,根据定义1可以得出专 由引理1中的2)有R,<R。与R=四xR矛盾。 家e:给出的属性的优劣顺序。由定义2判断P是 又由于,≥0,对C中任意的属性c,和c,有 否具有可接受一致性,如果P:不具有可接受一致 1-t≤rp-Tp≤t-1 性,必须进行相应的调整,否则无法判断属性的优 相应地, 劣。如果P具有可接受一致性,当考虑到专家的权 R's-R'=(R-Tp)-(R-T)= 重时,可将属性c:优于c,的优先度指数定义为 (R6-R,)+(Tp-Tp) 式中:Ra和R',分别是ca和c,在C'=C\{c,}中的 ,含 优先度指数。 从而得出属性c:在C中的优先度指数R:,即
2) ci > cj 当且仅当对 ∀k ∈ T 都有 c k i > c k j 。 定义 5 设 cp 为 C 中的一个属性,则有: 1)如果存在 ci ∈ C, 使得 cp ≤ ci 成立,则称 cp 为 C 中的劣属性; 2)如果不存在 ci ∈C, 使得 cp ≤ci 成立,则称 cp 为 C 中的非劣属性; 3)如果对 ∀ci ∈ C, 都有 ci ≤ cp, 则称 cp 为 C 中的优属性; 4)如果对 ∀ci ∈ C (i ≠ p), 都有 ci < cp, 则称 cp 为 C 中的最优属性。 从上述的定义可以得到: 引理 1: 1)如果 cp 为 C 中的优属性,则有 Rp = max 1≤j≤m Rj; 2)设 cp,cq ∈ C, 如果 cq ≤ cp, 则有① rqq < rpq; ② Rq < Rp; 3)令 cp 为 C 中的一个属性,如果 Rp = max 1≤j≤m Rj, 则 cp 为 C 中的一个非劣属性。 定理 1 设 cp,cq ∈ C, 如果 Rq = max 1≤j≤m,j≠p Rj, 则 cq 为 C′ = C \{cp} 中的非劣属性。 证明 假设 cq 不是 C′ 中的非劣属性,则存在 ck ∈C′, 使得 cq ≤ ck 。 因此由引理 1 中 2)知 Rq < Rk, 这与 Rq = max 1≤j≤m,j≠p Rj 矛盾,定理 1 得证。 定理 2 设 cp,ch ,cq ∈ C, Rp = max 1≤j≤m Rj, 这里 Rj 是 cj 的优先度指数。 如果 | Rh - Rq | > t - 1, 则 ch 和 cq 的序关系在 C′ = C \cp 中是不变的。 证明 因为 Rp = max 1≤j≤m Rj ,由引理 1 中 3)知 cp 为 C 中的一个非劣属性。 现证明对 ∀j ∈ M, 均有 rjp ≤ t - 1。 假设不成 立,则存在 cj0 ∈C, 使得 rj0 p = t 或者 rj0 p = t - 1 / 2。 因 此对 ∀k ∈ T, 都有 r k j0 p ≥ 1 2 且存在 k0 ∈ T, 使得 r k0 j0 p =1。 从而对 ∀k ∈ T, 都有 c k p ≤ c k j0 且存在 k0 ∈ T, 使得 c k0 p < c k0 j0 成立。 故由定义 4,有 cp ≤ cj0 。 再 由引理 1 中的 2)有 Rp < Rj0 与 Rp = max 1≤j≤m Rj 矛盾。 又由于 rjp ≥ 0, 对 C 中任意的属性 ch 和 cq, 有 1 - t ≤ rhp - rqp ≤ t - 1 相应地, R′h - R′q = (Rh - rhp) - (Rq - rqp) = (Rh - Rq) + (rqp - rhp) 式中: R′h 和 R′q 分别是 ch 和 cq 在 C′ = C \{cp} 中的 优先度指数。 由于 | Rh - Rq | > t - 1, 有:当 Rh > Rq 时, R′h > R′q; 当 Rh < Rq 时, R′h < R′q。 以上 2 个定理表明在属性的优劣排序中,找到 了 C 中最优的属性后,下一个最优属性是剩余属性 中的最优属性。 定理 1 表明如果 ci (i ∈ M) 在 C 中 的优先度指数最大,它就是最优属性。 专家们形成的群体决策应尽量接近于每一个专 家的偏好效用或意见,给专家赋权时,由不同的专家 给出的判断矩阵越接近,表明专家的意见越一致。 因此可以采用互补判断矩阵间的相似性度量来决定 专家的权重。 定义 6 设 Pu 和 Pv 为专家 eu 和 ev 给出的关于 属性偏好的互补判断矩阵,其中 eu ,ev ∈ E, 定义 2 个互补判断矩阵的相似接近度为 s(Pu ,Pv) = ∑ m j = 1 ∑ m i = 1 (p u ij + p v ij) - ∑ m j = 1 ∑ m i = 1 | p u ij - p v ij | ∑ m j = 1 ∑ m i = 1 (p u ij + p v ij) + ∑ m j = 1 ∑ m i = 1 | p u ij - p v ij | (1) 从而可以构造相似性矩阵 S 为 S = 1 s12 … s1t s21 1 … s2t ︙ ︙ ︙ st1 st2 … 1 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú 式中: suv = s(Pu ,Pv), 如果 u = v, 则有 suv = 1。 专家 eu 的平均相似接近度为 A(eu ) = 1 t - 1∑t suv (2) 通过 A(eu ) 来确定专家 eu 的权重为 λu = A(eu ) ∑ t u = 1 A(eu ) (3) 设 Pk = (p k ij) m×m (k ∈ T) 为专家 ek 给出的关于 属性集 C 的互补判断矩阵,根据定义 1 可以得出专 家 ek 给出的属性的优劣顺序。 由定义 2 判断 Pk 是 否具有可接受一致性,如果 Pk 不具有可接受一致 性,必须进行相应的调整,否则无法判断属性的优 劣。 如果 Pk 具有可接受一致性,当考虑到专家的权 重时,可将属性 ci 优于 cj 的优先度指数定义为 rij = ∑ t k = 1 λk r k ij 从而得出属性 ci 在 C 中的优先度指数 Ri, 即 第 2 期 吕智颖,等:一种带有属性偏好的模糊多属性决策方法 ·229·

.230. 智能系统学报 第10卷 (4) 文献[4]将梯形模糊数P分成3个平面图形, 分别为三角形ABP,矩形BPQC和三角形QCD,如 通过属性c:在C中的优先度指数R:来判定属 图2所示。记这3个图形的中心点分别为G,、G,和 性的权重,其中 G3,该文证明了这三点不在一条直线上,从而构成 w,=R,/(∑R),i∈M (5) 了三角形。 综上,专家权重和属性权重的计算过程如图1。 定义84】设P=(a,b,c,d;w)是R上的-个 专家给出的互补判断矩阵 梯形模糊数,三角形G,G,G3的外接圆的圆心坐标为 (xo,o)=(a+26+2e+d 是否具有可接受一致 6 N (2a+b-3c)(2d+c-3b)+5w2 (6) 12w 调整互补判断矩阵,使其具有 可接受一致性 圆心A:与坐标原点之间所形成的矩形面积为 互补判断矩阵的相似接近度 gg=(xa):(yo)月 (7) 确定专家权重 专家对属性集的偏序 属性的优势度 P(b,w)O(c.w) 确定属性权重 图1属性权重的确定 Fig.I The step of determining the attribute weights 1.2方案的排序或择优 梯形模糊数通常用4个参数来表示一个区间 数a,例如P=(a,b,c,d),且a≤b≤c≤d,其中 A(a,0)B(b.0)C(c,0)D(d,0)X a和d分别表示区间数取值的上限和下限,(b,c) 图2梯形模糊数 表示区间数在此范围内可能性最大。 Fig.2 Trapezoidal fuzzy number 当用区间模糊数表示一个模糊量时,为了覆盖 文献[4]根据梯形模糊数P通过式(6)和式(7)得 整个取值范围,区间可能会取得过大并且认为在整 出的g:的值来比较模糊数的大小,g:越大,则相应的 个区间内,取值是均等的,结果容易产生较大的偏 梯形模糊数P越大,并证明了其合理性。因此可以用 差。用梯形模糊数进行决策时,不仅保留了参数的 这种模糊数排序的方法来对方案进行排序或择优。 取值区间,而且还能突出取值可能性最大的范围,可 基于简单加权平均法则对规范化的决策矩阵 以弥补区间数的不足。 下面给出梯形模糊数的定义如下: F=(f)nxm及权重向量w=[ω1w2…wm]进 定义74]一个模糊数P=(a,b,c,d:w)被称 行集结,得到各方案的模糊综合评估值为 为梯形模糊数,如果其隶属函数为 w(t-a) 月=2i -,a≤t≤b b-a j= w,b≤t≤c u(t)= w(t-d) 设将F,分成如图2的3部分后得到的外接圆 c-d ,c≤t≤d 心O:=(f,f)与原点之间形成的矩形面积为S:= 0,其他 ff,则S:越大,方案A:越优。 式中:-n<a≤b≤c≤d<+0,0≤w≤1是- 2应用案例 个常数,如果w=1,则P=(a,b,c,d;1)是一个正 在投资决策过程中,对投资方案进行经济评价 规梯形模糊数,也可记为P=(a,b,c,d)
Ri = ∑ m j = 1 rij = ∑ t k = 1∑ m j = 1 λk rij (4) 通过属性 ci 在 C 中的优先度指数 Ri 来判定属 性的权重,其中 ωi = Ri / (∑ m i = 1 Ri),i ∈ M (5) 综上,专家权重和属性权重的计算过程如图 1。 图 1 属性权重的确定 Fig.1 The step of determining the attribute weights 1.2 方案的排序或择优 梯形模糊数通常用 4 个参数来表示一个区间 数[14] ,例如 P ~ = (a,b,c,d), 且 a ≤ b ≤ c ≤ d, 其中 a 和 d 分别表示区间数取值的上限和下限, (b,c) 表示区间数在此范围内可能性最大。 当用区间模糊数表示一个模糊量时,为了覆盖 整个取值范围,区间可能会取得过大并且认为在整 个区间内,取值是均等的,结果容易产生较大的偏 差。 用梯形模糊数进行决策时,不仅保留了参数的 取值区间,而且还能突出取值可能性最大的范围,可 以弥补区间数的不足。 下面给出梯形模糊数的定义如下: 定义 7 [4 ] 一个模糊数 P ~ = (a,b,c,d;ω) 被称 为梯形模糊数,如果其隶属函数为 μ p ~ (t) = ω(t - a) b - a ,a ≤ t ≤ b ω,b ≤ t ≤ c ω(t - d) c - d ,c ≤ t ≤ d 0,其他 ì î í ï ï ï ï ï ï ï ï 式中: - ¥ < a ≤ b ≤ c ≤ d < + ¥, 0 ≤ ω ≤ 1 是一 个常数,如果 ω = 1, 则 P ~ = (a,b,c,d;1) 是一个正 规梯形模糊数,也可记为 P ~ = (a,b,c,d) 。 文献[4]将梯形模糊数 P ~ 分成 3 个平面图形, 分别为三角形 ABP, 矩形 BPQC 和三角形 QCD, 如 图 2 所示。 记这 3 个图形的中心点分别为 G1 、G2 和 G3 , 该文证明了这三点不在一条直线上,从而构成 了三角形。 定义 8 [ 4 ] 设 P ~ = (a,b,c,d;ω) 是 R 上的一个 梯形模糊数,三角形 G1G2G3 的外接圆的圆心坐标为 (x - 0 ,y - 0 ) = ( a + 2b + 2c + d 6 , (2a + b - 3c)(2d + c - 3b) + 5ω 2 12ω ) (6) 圆心 A P ~ 与坐标原点之间所形成的矩形面积为 g p ~ = (x - 0 ) P ~ (y - 0 ) P ~ (7) 图 2 梯形模糊数 Fig.2 Trapezoidal fuzzy number 文献[4]根据梯形模糊数 P ~ 通过式(6)和式(7)得 出的 gP ~ 的值来比较模糊数的大小, gP ~ 越大,则相应的 梯形模糊数 P ~ 越大,并证明了其合理性。 因此可以用 这种模糊数排序的方法来对方案进行排序或择优。 基于简单加权平均法则对规范化的决策矩阵 F = ( f ~ ij)n×m 及权重向量 ω = [ω1 ω2 … ω m ] 进 行集结,得到各方案的模糊综合评估值为 F ~ i = (ai,bi,ci,di) = ∑ m j = 1 f ~ ijωj = (∑ m j = 1 aijωj,∑ m j = 1 bijωj,∑ m j = 1 cijωj,∑ m j = 1 dijωj),i ∈ N 设将 F ~ i 分成如图 2 的 3 部分后得到的外接圆 心 Oi =(f x i ,f y i ) 与原点之间形成的矩形面积为 Si = f x i f y i ,则 Si 越大,方案 Ai 越优。 2 应用案例 在投资决策过程中,对投资方案进行经济评价 ·230· 智 能 系 统 学 报 第 10 卷
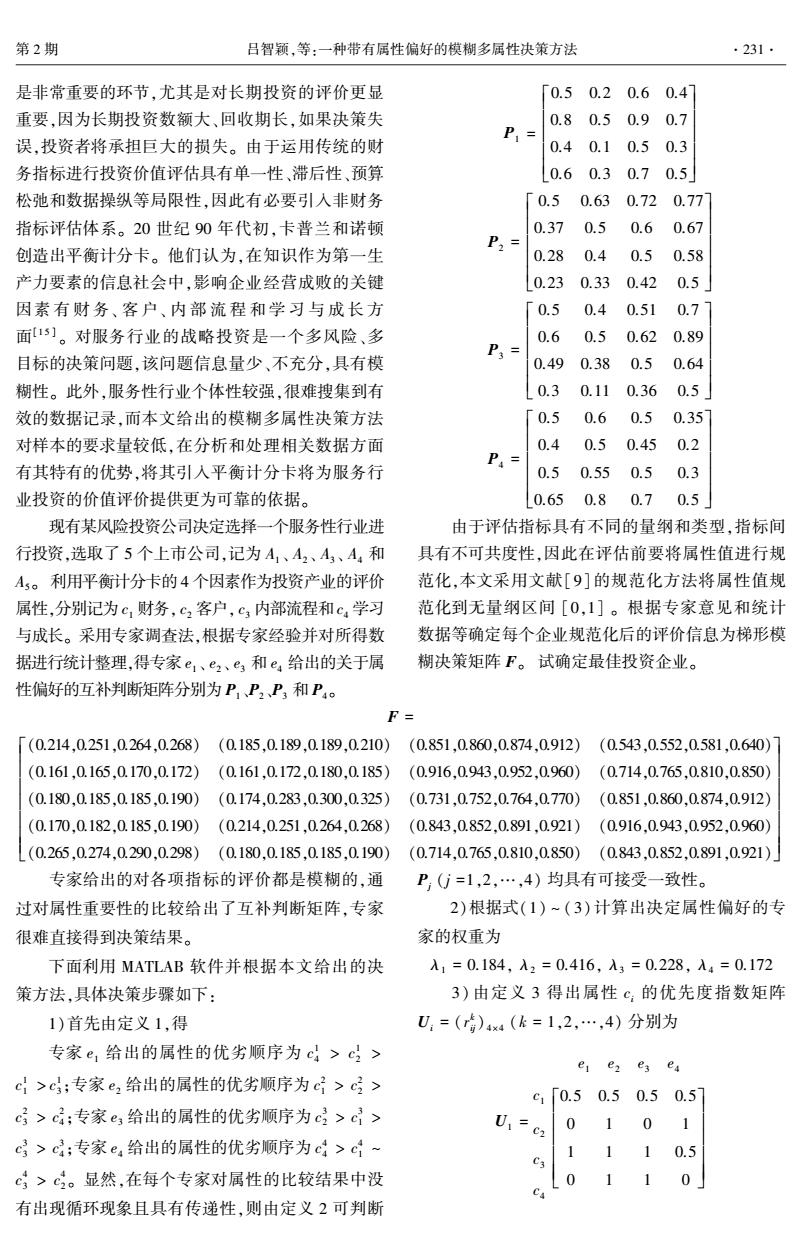
第2期 吕智颖,等:一种带有属性偏好的模糊多属性决策方法 .231· 是非常重要的环节,尤其是对长期投资的评价更显 「0.50.20.60.47 重要,因为长期投资数额大、回收期长,如果决策失 0.80.50.9 0.7 误,投资者将承担巨大的损失。由于运用传统的财 P1= 0.4 0.10.5 0.3 务指标进行投资价值评估具有单一性、滞后性、预算 0.6 0.3 0.70.5 松弛和数据操纵等局限性,因此有必要引入非财务 0.5 0.630.720.77 指标评估体系。20世纪90年代初,卡普兰和诺顿 0.37 0.5 0.60.67 创造出平衡计分卡。他们认为,在知识作为第一生 P2= 0.28 0.4 0.5 0.58 产力要素的信息社会中,影响企业经营成败的关键 0.23 0.330.420.5」 因素有财务、客户、内部流程和学习与成长方 「0.5 0.4 0.51 0.71 面5们。对服务行业的战略投资是一个多风险、多 0.6 0.5 0.620.89 目标的决策问题,该问题信息量少、不充分,具有模 P3= 0.49 0.38 0.5 0.64 糊性。此外,服务性行业个体性较强,很难搜集到有 0.3 0.11 0.36 0.5」 效的数据记录,而本文给出的模糊多属性决策方法 「0.5 0.6 0.5 0.35 对样本的要求量较低,在分析和处理相关数据方面 0.4 0.5 0.45 0.2 有其特有的优势,将其引入平衡计分卡将为服务行 P4= 0.5 0.55 0.5 0.3 业投资的价值评价提供更为可靠的依据。 10.65 0.80.7 0.5」 现有某风险投资公司决定选择一个服务性行业进 由于评估指标具有不同的量纲和类型,指标间 行投资,选取了5个上市公司,记为A1、A2、A、A和 具有不可共度性,因此在评估前要将属性值进行规 A5。利用平衡计分卡的4个因素作为投资产业的评价 范化,本文采用文献[9]的规范化方法将属性值规 属性,分别记为c,财务,c2客户,c3内部流程和c,学习 范化到无量纲区间[0,1]。根据专家意见和统计 与成长。采用专家调查法,根据专家经验并对所得数 数据等确定每个企业规范化后的评价信息为梯形模 据进行统计整理,得专家e、e2、e和e,给出的关于属 糊决策矩阵F。试确定最佳投资企业。 性偏好的互补判断矩阵分别为P,、P2、P,和P4。 F= (0.214,0.251,0.264,0.268)(0.185,0.189,0.189,0.210)(0.851,0.860,0.874,0.912)(0.543,0.552,0.581,0.640) (0.161,0.165,0.170,0.172)(0.161,0.172,0.180,0.185)(0.916,0.943,0.952,0.960)(0.714,0.765,0.810,0.850) (0.180,0.185,0.185,0.190)(0.174,0.283,0.300,0.325)(0.731,0.752,0.764,0.770) (0.851,0.860,0.874,0.912) (0.170.0.182.0.185,0.190)(0.214,0.251,0.264.0.268)(0.843,0.852.0.891,0.921)(0.916.0.943,0.952,0.960) (0.265,0.274,0.290,0.298)(0.180,0.185,0.185,0.190)(0.714,0.765,0.810,0.850)(0.843,0.852,0.891,0.921) 专家给出的对各项指标的评价都是模糊的,通 P(G=1,2,…,4)均具有可接受一致性。 过对属性重要性的比较给出了互补判断矩阵,专家 2)根据式(1)~(3)计算出决定属性偏好的专 很难直接得到决策结果。 家的权重为 下面利用MATLAB软件并根据本文给出的决 入1=0.184,入2=0.416,入3=0.228,入4=0.172 策方法,具体决策步骤如下: 3)由定义3得出属性c:的优先度指数矩阵 1)首先由定义1,得 U=(r)4x4(k=1,2,…,4)分别为 专家e,给出的属性的优劣顺序为c4>c> e e2 es es ci>c3;专家e2给出的属性的优劣顺序为c>c> c1「0.50.50.50.5 c>c;专家e给出的属性的优劣顺序为c>c> U 0 1 0 1 c>c;专家e,给出的属性的优劣顺序为c>c4~ 11 1 0.5 c>©。显然,在每个专家对属性的比较结果中没 1 1 0 Ca 有出现循环现象且具有传递性,则由定义2可判断
是非常重要的环节,尤其是对长期投资的评价更显 重要,因为长期投资数额大、回收期长,如果决策失 误,投资者将承担巨大的损失。 由于运用传统的财 务指标进行投资价值评估具有单一性、滞后性、预算 松弛和数据操纵等局限性,因此有必要引入非财务 指标评估体系。 20 世纪 90 年代初,卡普兰和诺顿 创造出平衡计分卡。 他们认为,在知识作为第一生 产力要素的信息社会中,影响企业经营成败的关键 因素 有 财 务、 客 户、 内 部 流 程 和 学 习 与 成 长 方 面[1 5 ] 。 对服务行业的战略投资是一个多风险、多 目标的决策问题,该问题信息量少、不充分,具有模 糊性。 此外,服务性行业个体性较强,很难搜集到有 效的数据记录,而本文给出的模糊多属性决策方法 对样本的要求量较低,在分析和处理相关数据方面 有其特有的优势,将其引入平衡计分卡将为服务行 业投资的价值评价提供更为可靠的依据。 现有某风险投资公司决定选择一个服务性行业进 行投资,选取了 5 个上市公司,记为 A1、 A2、 A3、 A4 和 A5。 利用平衡计分卡的 4 个因素作为投资产业的评价 属性,分别记为 c1 财务, c2 客户, c3 内部流程和 c4 学习 与成长。 采用专家调查法,根据专家经验并对所得数 据进行统计整理,得专家 e1、 e2、 e3 和 e4 给出的关于属 性偏好的互补判断矩阵分别为 P1、P2、P3 和 P4。 P1 = 0.5 0.2 0.6 0.4 0.8 0.5 0.9 0.7 0.4 0.1 0.5 0.3 0.6 0.3 0.7 0.5 é ë ê ê ê ê ê ù û ú ú ú ú ú P2 = 0.5 0.63 0.72 0.77 0.37 0.5 0.6 0.67 0.28 0.4 0.5 0.58 0.23 0.33 0.42 0.5 é ë ê ê ê ê ê ù û ú ú ú ú ú P3 = 0.5 0.4 0.51 0.7 0.6 0.5 0.62 0.89 0.49 0.38 0.5 0.64 0.3 0.11 0.36 0.5 é ë ê ê ê ê ê ù û ú ú ú ú ú P4 = 0.5 0.6 0.5 0.35 0.4 0.5 0.45 0.2 0.5 0.55 0.5 0.3 0.65 0.8 0.7 0.5 é ë ê ê ê ê ê ù û ú ú ú ú ú 由于评估指标具有不同的量纲和类型,指标间 具有不可共度性,因此在评估前要将属性值进行规 范化,本文采用文献[9]的规范化方法将属性值规 范化到无量纲区间 [0,1] 。 根据专家意见和统计 数据等确定每个企业规范化后的评价信息为梯形模 糊决策矩阵 F。 试确定最佳投资企业。 F = (0.214,0.251,0.264,0.268) (0.185,0.189,0.189,0.210) (0.851,0.860,0.874,0.912) (0.543,0.552,0.581,0.640) (0.161,0.165,0.170,0.172) (0.161,0.172,0.180,0.185) (0.916,0.943,0.952,0.960) (0.714,0.765,0.810,0.850) (0.180,0.185,0.185,0.190) (0.174,0.283,0.300,0.325) (0.731,0.752,0.764,0.770) (0.851,0.860,0.874,0.912) (0.170,0.182,0.185,0.190) (0.214,0.251,0.264,0.268) (0.843,0.852,0.891,0.921) (0.916,0.943,0.952,0.960) (0.265,0.274,0.290,0.298) (0.180,0.185,0.185,0.190) (0.714,0.765,0.810,0.850) (0.843,0.852,0.891,0.921) é ë ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú 专家给出的对各项指标的评价都是模糊的,通 过对属性重要性的比较给出了互补判断矩阵,专家 很难直接得到决策结果。 下面利用 MATLAB 软件并根据本文给出的决 策方法,具体决策步骤如下: 1)首先由定义 1,得 专家 e1 给出的属性的优劣顺序为 c 1 4 > c 1 2 > c 1 1 > c 1 3 ;专家 e2 给出的属性的优劣顺序为 c 2 1 > c 2 2 > c 2 3 > c 2 4 ;专家 e3 给出的属性的优劣顺序为 c 3 2 > c 3 1 > c 3 3 > c 3 4 ;专家 e4 给出的属性的优劣顺序为 c 4 4 > c 4 1 ~ c 4 3 > c 4 2 。 显然,在每个专家对属性的比较结果中没 有出现循环现象且具有传递性,则由定义 2 可判断 Pj (j =1,2,…,4) 均具有可接受一致性。 2)根据式(1) ~ (3) 计算出决定属性偏好的专 家的权重为 λ1 = 0.184, λ2 = 0.416, λ3 = 0.228, λ4 = 0.172 3) 由定义 3 得出属性 ci 的优先度指数矩阵 Ui = (r k ij)4×4 (k = 1,2,…,4) 分别为 U1 = c1 c2 c3 c4 e1 e2 e3 e4 0.5 0.5 0.5 0.5 0 1 0 1 1 1 1 0.5 0 1 1 0 é ë ê ê ê ê ê ù û ú ú ú ú ú 第 2 期 吕智颖,等:一种带有属性偏好的模糊多属性决策方法 ·231·

·232. 智能系统学报 第10卷 05=(0.459,0.416) e e2 es ea 进而又因式(9)得出这些点与坐标原点之间形 c1「1 0 1 07 成的矩形面积即方案的综合评价值分别为S,= U2= 0.50.50.50.5 0.168,S2=0.179,S3=0.189,S4=0.200,S4= 1 1 1 0 C3 0.190。 1 1 0」 CA ee2 es ea 0 0 0 0.51 F U3= 0 0 0 1 0.50.50.50.5 C3 F:- 0 1 1 0 e e2 es 图3梯形模糊数 Fig.3 Trapezoidal fuzzy numbers and their circum- c1「1 0 centers of centroids U,c2 0 0 0 综上,得出方案的优劣顺序为 C3 0 0 1 0.50.50.50.5 A4>A5>A3>A2>A1 Ca 从而得出最佳投资公司为A,其次为A5。 4)由式(4)计算每个属性c:在C中的优先度指 数分别为R1=2.4155,R2=2.564,R3=1.3715, 3结束语 R4=1.649进而由式(5)计算属性的权重为w1= 本文基于判断矩阵信息获得属性权重,并且给 0.302,w2=0.321,w3=0.171,w4=0.206。可见客 出了一种方案排序或择优的方法,从而丰富和发展 户的权重最大,其次是财务指标的权重,这与服务性 了模糊多属性决策方法。采用正的梯形模糊数表达 行业的服务性有很大的联系,因此顾客的满意度对 专家的评估意见并且给出了互补判断矩阵相似度和 投资能否实起到了关键的作用。 属性优势度的定义更能反映专家偏好的模糊性,使 5)由式(8)集结权重向量ω和模糊决策矩阵 模型更加符合实际情况,计算简便,避免了规划求解 F,得到如图3所示的关于每个备选方案A:,i=1, 的繁琐过程。该方法可以弥补平衡计分卡的不足, 2,…,5的模糊评价值为 有助于企业对投资评价做出更为科学准确的判断, F1=(0.381,0.397,0.410,0.436) 便于管理人员在实践中应用。 F2=(0.404,0.424,0.439,0.451) F3=(0.411,0.452,0.463,0.481) 参考文献: F4=(0.453,0.475,0.489,0.499) [1]张荣,刘思峰.一种基于判断矩阵信息的多属性群决策 F3=(0.434,0.448,0.469,0.486) 方法[J].系统工程与电子技术,2009,31(2):373-375. 6)模糊综合评估值F:,(i=1,2,…,5)按照如 ZHANG Rong,LIU Sifeng.Multi-attribute decision making 图2所示的方法分块后得到的外接圆的圆心坐标分 method based on the information of judgment matrixes[J]. 别为 Systems Engineering and Electronics,2009,31(2):373- 01=(0.405,0.416) 375. 02=(0.430,0.416) [2]陈晓红,刘益凡.基于区间数群决策矩阵的专家权重确 03=(0.454,0.416) 定方法及其算法实现[J].系统工程与电子技术,2010, 04=(0.480,0.416) 329(10):2128-2131. CHEN Xiaohong,LIU Yifan.Expert weights determination
U2 = c1 c2 c3 c4 e1 e2 e3 e4 1 0 1 0 0.5 0.5 0.5 0.5 1 1 1 0 1 1 1 0 é ë ê ê ê ê ê ù û ú ú ú ú ú U3 = c1 c2 c3 c4 e1 e2 e3 e4 0 0 0 0.5 0 0 0 1 0.5 0.5 0.5 0.5 0 1 1 0 é ë ê ê ê ê ê ù û ú ú ú ú ú U4 = c1 c2 c3 c4 e1 e2 e3 e4 1 0 0 1 0 0 0 1 1 0 0 1 0.5 0.5 0.5 0.5 é ë ê ê ê ê ê ù û ú ú ú ú ú 4)由式(4)计算每个属性 ci 在 C 中的优先度指 数分别为 R1 = 2.415 5, R2 = 2.564, R3 = 1.371 5, R4 =1.649 进而由式( 5) 计算属性的权重为 ω1 = 0.302, ω2 = 0.321, ω3 = 0.171, ω4 = 0.206。 可见客 户的权重最大,其次是财务指标的权重,这与服务性 行业的服务性有很大的联系,因此顾客的满意度对 投资能否实起到了关键的作用。 5)由式(8) 集结权重向量 ω 和模糊决策矩阵 F, 得到如图 3 所示的关于每个备选方案 Ai,i = 1, 2,…,5 的模糊评价值为 F1 = (0.381,0.397,0.410,0.436) F2 = (0.404,0.424,0.439,0.451) F3 = (0.411,0.452,0.463,0.481) F4 = (0.453,0.475,0.489,0.499) F5 = (0.434,0.448,0.469,0.486) 6)模糊综合评估值 Fi,(i = 1,2,…,5) 按照如 图 2 所示的方法分块后得到的外接圆的圆心坐标分 别为 O1 = (0.405,0.416) O2 = (0.430,0.416) O3 = (0.454,0.416) O4 = (0.480,0.416) O5 = (0.459,0.416) 进而又因式(9)得出这些点与坐标原点之间形 成的矩形面积即方案的综合评价值分别为 S1 = 0.168 , S2 = 0.179, S3 = 0.189, S4 = 0.200, S4 = 0.190。 图 3 梯形模糊数 Fig.3 Trapezoidal fuzzy numbers and their circum⁃ centers of centroids 综上,得出方案的优劣顺序为 A4 > A5 > A3 > A2 > A1 从而得出最佳投资公司为 A4 , 其次为 A5 。 3 结束语 本文基于判断矩阵信息获得属性权重,并且给 出了一种方案排序或择优的方法,从而丰富和发展 了模糊多属性决策方法。 采用正的梯形模糊数表达 专家的评估意见并且给出了互补判断矩阵相似度和 属性优势度的定义更能反映专家偏好的模糊性,使 模型更加符合实际情况,计算简便,避免了规划求解 的繁琐过程。 该方法可以弥补平衡计分卡的不足, 有助于企业对投资评价做出更为科学准确的判断, 便于管理人员在实践中应用。 参考文献: [1]张荣,刘思峰. 一种基于判断矩阵信息的多属性群决策 方法[J]. 系统工程与电子技术, 2009, 31(2): 373⁃375. ZHANG Rong, LIU Sifeng. Multi⁃attribute decision making method based on the information of judgment matrixes[ J]. Systems Engineering and Electronics, 2009, 31( 2): 373⁃ 375. [2]陈晓红,刘益凡. 基于区间数群决策矩阵的专家权重确 定方法及其算法实现[ J].系统工程与电子技术, 2010, 329(10): 2128⁃2131. CHEN Xiaohong, LIU Yifan. Expert weights determination ·232· 智 能 系 统 学 报 第 10 卷

第2期 吕智颖,等:一种带有属性偏好的模糊多属性决策方法 .233. method and realization algorithm based on interval numbers ronment[J].CAAI Transactions on Intelligent Systems, group decision matrices[J].Systems Engineering and Elec- 2010.5(4):283-291. tronics,2010,329(10):2128-2131. [12]赵克勤.基于集对分析的不确定多属性决策模型与算法 [3]宋光兴,邹平.多属性群决策中专家的权重确定方法[J]. [J].智能系统学报,2010,5(1):41-50. 系统工程,2001,19(4):84-89. ZHAO Keqin.Decision making algorithm based on set pair SONG Guangxing,ZOU Ping.The method of determining analysis for use when facing multiple uncertain attributes the weight of the decision-maker in multi-attribute group de- [J].CAAI Transactions on Intelligent Systems,2010,5 cision making[J].Systems Engineering,2001,19(4):84- (1):41-50. 89 [13]樊治平,姜艳萍.互补判断矩阵一致性改进方法[J].东 [4]RAO P B,SHANKAR N R.Ranking fuzzy numbers with 北大学学报:自然科学版,2003,24(1):98-101. an area method using circumcenter of centroids[J].Fuzzy FAN Zhiping,JIANG Yanping.Improving method for the Information and Engineering,2013,1:3-18. consistency of reciprocal judgement matrix[J].Journal of [5]ABBASBANDY S.A new approach for ranking of trapezoidal Northeastern University:Natural Science,2003,24(1): fuzzy numbers[J].Computers and Mathematics with Appli- 98-101. cations,2009,57(3):413-419. [14]朱方霞,陈华友.区间多属性决策问题研究综述[J].模 [6]CHU T C,TASAO C T.Ranking fuzzy numbers with an area 糊系统与数学,2013,27(3):149-159. between the centroid point and original point[].Computers ZHU Fangxia,CHEN Huayou.An review on the interval and Mathematics with Applications,2002,43:111-117. multi-attribute decision making problem[J].Fuzz Systems [7]YU V F,CHI H T X DAT L Q,et al.Ranking general- and Mathematics,2013,27(3):149-159. ized fuzzy numbers in fuzzy decision making based on the [15]罗伯特·卡普兰,大卫·诺顿.平衡计分卡一化战略为 left and right transfer coefficients and areas[J].Applied 行动[M].广州:广东经济出版社,2005:49-59. Mathematics Modeling,2013,37:8106-8117. 作者简介: [8]魏存平,邱菀华,王新哲.一种新的模糊群体决策方法 [J].系统工程理论与实践,2001(7):81-86. 吕智颖.女,1979年生,讲师.博士 WEI Cunping,QIU Wanhua,WANG Xinzhe.A new ap- 研究生,主要研究方向为智能系统决 proach of group decision making under fuzzy preference[] 策、模糊决策,发表学术论文10余篇。 Systems Engineering Theory and Practice,2001(7):81-86. [9]吕智颖,黄天民,靳凤霞.模糊多属性格序决策的冗余指 标的消除策略[J].数学的实践与认识,2013,43(10): 黄天民,男.1958年生,教授,博士 173.181 生导师,主要研究方向为智能系统优化 LV Zhiying,HUANG Tianmin,JIN Fengxia.Fuzzy multiple 与控制、智能信息处理及其在电气系统 attribute lattice decision making method based on the elimi- 中的应用。发表学术论文50余篇,出 nation of redundant similarity index[J].Mathematics in 版著作1部。 Practice and Theory,2013,43(10):173-181 [10]XIAO Z,XIA S,GONG K,et al.The trapezoidal fuzzy soft set and its application in MCDM[J].Appl Math Mod- 梁学章,男,1939年生,教授,博士 el1.2012.36:5844-5855. 生导师,主要研究方向为数值逼近。发 [11]冯珊,郭四海.采办协同工程中的不确定多属性决策技 表学术论文147篇,其中被SCI收录 术[J].智能系统学报,2010,5(4):283-291 18篇,被EI收录32篇,被ISTP收录 FENG Shan,GUO Sihai.Uncertain multiple attribute deci- 27篇,出版专著5部。 sion making techniques in a cooperative engineering envi
method and realization algorithm based on interval numbers group decision matrices[J]. Systems Engineering and Elec⁃ tronics, 2010, 329 (10): 2128⁃2131. [3]宋光兴,邹平.多属性群决策中专家的权重确定方法[ J]. 系统工程, 2001, 19(4): 84⁃89. SONG Guangxing, ZOU Ping. The method of determining the weight of the decision⁃maker in multi⁃attribute group de⁃ cision making[J]. Systems Engineering, 2001, 19(4): 84⁃ 89. [4]RAO P B , SHANKAR N R. Ranking fuzzy numbers with an area method using circumcenter of centroids[ J]. Fuzzy Information and Engineering, 2013, 1: 3⁃18. [5]ABBASBANDY S. A new approach for ranking of trapezoidal fuzzy numbers[J]. Computers and Mathematics with Appli⁃ cations, 2009, 57 (3): 413⁃419. [6]CHU T C, TASAO C T. Ranking fuzzy numbers with an area between the centroid point and original point[J]. Computers and Mathematics with Applications, 2002, 43: 111⁃117. [7]YU V F, CHI H T X , DAT L Q, et al. Ranking general⁃ ized fuzzy numbers in fuzzy decision making based on the left and right transfer coefficients and areas [ J]. Applied Mathematics Modeling, 2013, 37: 8106⁃8117. [8]魏存平,邱菀华,王新哲.一种新的模糊群体决策方法 [J]. 系统工程理论与实践, 2001(7): 81⁃86. WEI Cunping, QIU Wanhua, WANG Xinzhe. A new ap⁃ proach of group decision making under fuzzy preference[J]. Systems Engineering Theory and Practice, 2001(7): 81⁃86. [9]吕智颖,黄天民,靳凤霞. 模糊多属性格序决策的冗余指 标的消除策略[ J]. 数学的实践与认识, 2013, 43(10): 173⁃ 181. LV Zhiying, HUANG Tianmin, JIN Fengxia. Fuzzy multiple attribute lattice decision making method based on the elimi⁃ nation of redundant similarity index [ J ]. Mathematics in Practice and Theory, 2013, 43(10): 173⁃181. [10]XIAO Z, XIA S, GONG K, et al. The trapezoidal fuzzy soft set and its application in MCDM[J]. Appl Math Mod⁃ ell, 2012, 36: 5844⁃5855. [11]冯珊,郭四海. 采办协同工程中的不确定多属性决策技 术[J]. 智能系统学报, 2010, 5(4): 283⁃291. FENG Shan,GUO Sihai. Uncertain multiple attribute deci⁃ sion making techniques in a cooperative engineering envi ronment[ J]. CAAI Transactions on Intelligent Systems, 2010, 5(4): 283⁃291. [12]赵克勤.基于集对分析的不确定多属性决策模型与算法 [J]. 智能系统学报, 2010, 5(1): 41⁃50. ZHAO Keqin. Decision making algorithm based on set pair analysis for use when facing multiple uncertain attributes [J]. CAAI Transactions on Intelligent Systems, 2010, 5 (1): 41⁃50. [13]樊治平,姜艳萍. 互补判断矩阵一致性改进方法[J]. 东 北大学学报: 自然科学版, 2003, 24(1): 98⁃101. FAN Zhiping, JIANG Yanping. Improving method for the consistency of reciprocal judgement matrix[ J]. Journal of Northeastern University: Natural Science, 2003, 24( 1): 98⁃101. [14]朱方霞,陈华友. 区间多属性决策问题研究综述[J]. 模 糊系统与数学, 2013, 27(3): 149⁃159. ZHU Fangxia, CHEN Huayou. An review on the interval multi⁃attribute decision making problem[ J]. Fuzz Systems and Mathematics, 2013, 27(3): 149⁃159. [15]罗伯特·卡普兰,大卫·诺顿.平衡计分卡—化战略为 行动[M]. 广州:广东经济出版社, 2005: 49⁃59. 作者简介: 吕智颖,女,1979 年生,讲师,博士 研究生,主要研究方向为智能系统决 策、模糊决策,发表学术论文 10 余篇。 黄天民,男,1958 年生,教授,博士 生导师,主要研究方向为智能系统优化 与控制、智能信息处理及其在电气系统 中的应用。 发表学术论文 50 余篇,出 版著作 1 部。 梁学章,男,1939 年生,教授,博士 生导师,主要研究方向为数值逼近。 发 表学术论文 147 篇 ,其中被 SCI 收录 18 篇, 被 EI 收录 32 篇, 被 ISTP 收录 27 篇,出版专著 5 部。 第 2 期 吕智颖,等:一种带有属性偏好的模糊多属性决策方法 ·233·