
第10卷第2期 智能系统学报 Vol.10 No.2 2015年4月 CAAI Transactions on Intelligent Systems Apr.2015 D0:10.3969/j.issn.1673-4785.201401022 网络出版地址:htp:/www.cmki.net/kcms/detail/23.1538.TP.20150326.1020.008.html 六子棋中基于局部“路”扫描方式的博弈树生成算法 李学俊2,王小龙,吴蕾,刘慧婷 (1.安徽大学计算机科学与技术学院,安徽合肥230601:2.安徽大学计算智能与信号处理重点实验室,安徽合肥230039) 摘要:针对六子棋博弈比赛中基于“路”的全局扫描方式的博弈树生成算法效率较低问题,首先分析了基于“路”的 全局扫描方式的计算规则和估值分析,然后将博弈树生成算法中的全局扫描方式改进为局部扫描方式,并给出其计 算规则和估值分析,接着设计了基于局部扫描方式的博弈树生成算法,并集成到Alpha-Bta剪枝算法中。最后从搜 索效率和博弈水平2个角度对全局扫描和局部扫描进行实验,实验结果表明,局部扫描方式在比赛时间要求的情况 下,能够大幅度提高搜索效率,并且博弈水平显著优于全局扫描方式。 关键词:机器博弈:六子棋;路:局部扫描:博弈树:剪枝算法:估值 中图分类号:TP31文献标志码:A文章编号:1673-4785(2015)02-0267-06 中文引用格式:李学俊,王小龙,吴蕾,等.六子棋中基于局部“路"扫描方式的博奔树生成算法[J].智能系统学报,2015,10(2): 267-272. 英文引用格式:LI Xuejun,WANG Xiaolong,WU Lei,,etal.Game tree generation algorithm based on local-road scanning method for connect 6[J].CAAI Transactions on Intelligent Systems,2015,10(2):267-272. Game tree generation algorithm based on local-road scanning method for connect 6 LI Xuejun'2,WANG Xiaolong',WU Lei',LIU Huiting' (1.School of Computer Science and Technology,Anhui University,Hefei 230601,China;2.Intelligent Computing and Signal Process- ing Laboratory,Anhui University,Hefei 230039,China) Abstract:Aiming at the problem that the game-tree generation algorithm generated by global scanning method is low in efficiency in the connect 6,this paper analyzes the calculation rules and valuation analysis of the global scanning method based on "road".Secondly,it develops the global scanning method of the game-tree generation al- gorithm into local scanning method,and introduces the calculation rules and valuation analysis.The game-tree gen- eration algorithm is a local scanning method designed and integrated into the alpha-beta pruning search.Finally, the global and local scanning experiments are carried out from the two perspectives of search efficiency and playing skill.The experimental results showed that local scanning could greatly improve search efficiency within the compe- tition time.The game ability is superior to that of the global scanning method. Keywords:computer game;connect 6;road;local scanning;game tree;pruning algorithm;evaluation 机器博弈(即计算机博弈)是人工智能领域的 类从事智能活动。因为存在于棋类博弈的原则或许 分支,同时也是该领域公认的最具挑战性的研究课 就存在于人类的智能活动中。近年来,国内外计 题之一。棋类博弈是人类所能从事的智能活动之 算机博弈比赛,极大地推动了计算机博弈问题的研 一,如果可以掌握博弈的本质,也就说明可以帮助人 究,促进了计算机博弈理论和技术的发展。 棋类计算机博弈涉及的棋种较多,六子棋就是 收稿日期:2014-01-09.网络出版日期:2015-03-26 基金项目:国家自然科学基金资助项目(61202227). 其中之一,它由台湾国立交通大学吴毅成教授发明。 通信作者:李学俊.E-mail:xili@ahu.eu.cn. 六子棋竞赛规则很简单,对弈双方分别执黑子和白
第 10 卷第 2 期 智 能 系 统 学 报 Vol.10 №.2 2015 年 4 月 CAAI Transactions on Intelligent Systems Apr. 2015 DOI:10.3969 / j.issn.1673⁃4785.201401022 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20150326.1020.008.html 六子棋中基于局部“路”扫描方式的博弈树生成算法 李学俊1,2 ,王小龙1 ,吴蕾1 ,刘慧婷1 (1.安徽大学 计算机科学与技术学院,安徽 合肥 230601; 2.安徽大学 计算智能与信号处理重点实验室,安徽 合肥 230039) 摘 要:针对六子棋博弈比赛中基于“路”的全局扫描方式的博弈树生成算法效率较低问题,首先分析了基于“路”的 全局扫描方式的计算规则和估值分析,然后将博弈树生成算法中的全局扫描方式改进为局部扫描方式,并给出其计 算规则和估值分析,接着设计了基于局部扫描方式的博弈树生成算法,并集成到 Alpha⁃Beta 剪枝算法中。 最后从搜 索效率和博弈水平 2 个角度对全局扫描和局部扫描进行实验,实验结果表明,局部扫描方式在比赛时间要求的情况 下,能够大幅度提高搜索效率,并且博弈水平显著优于全局扫描方式。 关键词:机器博弈;六子棋;路;局部扫描;博弈树;剪枝算法;估值 中图分类号:TP31 文献标志码:A 文章编号:1673⁃4785(2015)02⁃0267⁃06 中文引用格式:李学俊,王小龙,吴蕾,等. 六子棋中基于局部“路”扫描方式的博弈树生成算法[ J]. 智能系统学报, 2015, 10( 2): 267⁃272. 英文引用格式:LI Xuejun, WANG Xiaolong, WU Lei, et al. Game tree generation algorithm based on local⁃road scanning method for connect 6[J]. CAAI Transactions on Intelligent Systems, 2015, 10(2): 267⁃272. Game tree generation algorithm based on local⁃road scanning method for connect 6 LI Xuejun 1,2 , WANG Xiaolong 1 , WU Lei 1 , LIU Huiting 1 (1.School of Computer Science and Technology, Anhui University, Hefei 230601, China; 2.Intelligent Computing and Signal Process⁃ ing Laboratory, Anhui University, Hefei 230039, China) Abstract: Aiming at the problem that the game⁃tree generation algorithm generated by global scanning method is low in efficiency in the connect 6, this paper analyzes the calculation rules and valuation analysis of the global scanning method based on " road" . Secondly, it develops the global scanning method of the game⁃tree generation al⁃ gorithm into local scanning method, and introduces the calculation rules and valuation analysis. The game⁃tree gen⁃ eration algorithm is a local scanning method designed and integrated into the alpha⁃beta pruning search. Finally, the global and local scanning experiments are carried out from the two perspectives of search efficiency and playing skill. The experimental results showed that local scanning could greatly improve search efficiency within the compe⁃ tition time. The game ability is superior to that of the global scanning method. Keywords:computer game; connect 6; road; local scanning; game tree; pruning algorithm; evaluation 收稿日期:2014⁃01⁃09. 网络出版日期:2015⁃03⁃26. 基金项目:国家自然科学基金资助项目(61202227). 通信作者:李学俊.E⁃mail:xjli@ ahu.edu.cn. 机器博弈(即计算机博弈)是人工智能领域的 分支,同时也是该领域公认的最具挑战性的研究课 题之一。 棋类博弈是人类所能从事的智能活动之 一,如果可以掌握博弈的本质,也就说明可以帮助人 类从事智能活动。 因为存在于棋类博弈的原则或许 就存在于人类的智能活动中[1] 。 近年来,国内外计 算机博弈比赛,极大地推动了计算机博弈问题的研 究,促进了计算机博弈理论和技术的发展。 棋类计算机博弈涉及的棋种较多,六子棋就是 其中之一,它由台湾国立交通大学吴毅成教授发明。 六子棋竞赛规则很简单,对弈双方分别执黑子和白

·268· 智能系统学报 第10卷 子,在19×19的方格棋盘上,除了黑子先手第1步落 常见的棋形种类较多,且每种棋形又存在多种落子 一颗子外,双方轮流落2颗子,先在水平、垂直或对 方式o,由此文献[11]提出“路”的扫描方式。所 角线上形成连续的6子(或6子以上)的一方为 谓“路”就在棋盘的水平、垂直或对角线上出现连续 胜[]。六子棋由五子棋改良而来,但是其复杂度却 6点连成一线[山。 远大于五子棋[3】,其中博弈树复杂度达到100,状 基于“路”扫描方式能有效降低棋形判断的复 态空间复杂度达到10”,仅次于围棋,与象棋相当 杂度,通过“路”扫描方式的估值相对于通过棋形扫 或略高4。 描方式估值较为简单,实现方面也更加容易,并且搜 作为刚兴起不久的棋类游戏,六子棋的智能搜 索时间较短。文献[12]在传统的基于“路”的全局 索算法研究较少。博弈树搜索为计算机博弈的基本 扫描方式上采用自学习的方法自动调整估值函数的 搜索算法,它是从根节点向下递归搜索而产生的包 参数,提高搜索精度。文献[l3]在应用Alpha-Beta 含双方所有对弈过程的搜索树。由于受搜索时间的 剪枝搜索时引入并行计算,大幅度提高搜索效率。 严格约束,博弈树能够搜索到的叶子节点极少属于 “路”扫描方式的引入避免了精确判断棋形的 末端节点(即根据对弈规则可以判定比赛结果),此 难题,减少了计算量:同时应用面向对象的思想,将 时需要通过估值函数对叶子节点进行量化计算,判 “路”的信息抽象成类,易于实现。基于“路”的扫 断该叶子节点所处的棋局状态是有利于己方还是对 描方式解决了因棋形判断不准确而影响博弈水平的 方,且计算其有利程度大小)。 问题,但是应用博弈树搜索时,在对每个子节点的扩 在博弈树的扩展过程中会将双方可能的对弈过 展时都需要对棋盘进行全局扫描。受博弈竞赛时间 约束,搜索深度和宽度都有所限制,博弈水平也达不 程展示出来,首先对叶子节点进行估值,再倒推计算 根节点各分支节点的值,选择估值最大的分支节点 到理想要求。因此本文在博弈树生成子节点时将基 于“路”的全局扫描方式改进为局部扫描,并设计基 作为最佳解。但是随着搜索深度的增加,博弈树的 节点数量成指数性增长。在极大极小值算法的基础 于局部“路”扫描方式的博弈树生成算法。 上,Alpha-Beta剪枝技术在搜索的过程中忽略了无 1 基于“路”的全局扫描方式 用的节点,并将其删除,不对其估值,删除无用节点 1.1计算规则 时不会造成信息丢失,不影响根节点各分支节点的 估值,提高了搜索速度6。在深层次的递归搜索中 K子棋可用connect(m,n,k,p,g)表示14,对弈 双方为黑方和白方,黑方先走。connect(m,n,k,P,q) 广泛采用Alpha-Beta剪枝算法。为了提高计算速 的规则包括:1)棋盘的方格为m行n列,即含m×n个 度,本文采用Alpha-Beta剪枝技术。 交叉点:2)对弈时双方轮流落p颗棋子(根据六子棋 由于六子棋对弈规则的特殊性,如果只考虑单 比赛黑方先手规则,第1次落g颗棋子):3)在棋盘的 个棋子对棋局的影响进行估值计算,而未考虑棋子 水平、垂直或对角线上先形成k连获胜。若在规定时 间的位置关系,肯定会影响棋局状态的评估效果,由 间内双方均无法获胜,则判为平局。 此产生了基于棋形的扫描方式[。常见的棋形主 K子棋中“路”的计算规则:1)水平方向:m 要分为六连、长连、活五、眠五、死五、活四、眠四、死 行×(n-k+1)路/行,如图1中(a)所示;2)垂直 四、活三、眠三、朦胧三、活二、眠二、朦胧二等。 方向:n列×(m-k+1)路/列,类似于水平方向: 文献[2]提出基于棋形的数据表示方法,数据结构 3)左斜方向:由于k连需要k子连续相连,在左斜方 依赖于棋形,将棋局的数据表示和局面知识结合起 向前k一1行不可能形成k连,故左斜方向路数为 来,提高搜索效率。 (m-k+1)行×(n-k+1)路/行,如图1中(b): 基于棋形的扫描方式将棋子间的位置关系联系 4)右斜方向:(n-k+1)列×(m-k+1)路/列, 起来,通过产生某种棋形来表示对整个棋局状态的 类似于左斜方向。 影响程度,更具有直观性,减少对单个棋子进行估值 六子棋是K子棋的一种15),采用19×19方格 的不稳定性:然而目前棋形是通过经验总结的,人为 棋盘,可表示为connect(19,19,6,2,1),总路数为 因素影响很大,不排除还存在其他种类,这需要通过 大量实验来确定。大部分六子棋的估值计算都是基 Na=∑Nin(i)) (1) i=0 于棋形的扫描方式,但是由于棋形的判断要求很高, 式中:Nd表示六子棋全局扫描总路数
子,在 19×19 的方格棋盘上,除了黑子先手第 1 步落 一颗子外,双方轮流落 2 颗子,先在水平、垂直或对 角线上形成连续的 6 子( 或 6 子以上) 的一方为 胜[2] 。 六子棋由五子棋改良而来,但是其复杂度却 远大于五子棋[3] ,其中博弈树复杂度达到 10 140 ,状 态空间复杂度达到 10 172 ,仅次于围棋,与象棋相当 或略高[4] 。 作为刚兴起不久的棋类游戏,六子棋的智能搜 索算法研究较少。 博弈树搜索为计算机博弈的基本 搜索算法,它是从根节点向下递归搜索而产生的包 含双方所有对弈过程的搜索树。 由于受搜索时间的 严格约束,博弈树能够搜索到的叶子节点极少属于 末端节点(即根据对弈规则可以判定比赛结果),此 时需要通过估值函数对叶子节点进行量化计算,判 断该叶子节点所处的棋局状态是有利于己方还是对 方,且计算其有利程度大小[5] 。 在博弈树的扩展过程中会将双方可能的对弈过 程展示出来,首先对叶子节点进行估值,再倒推计算 根节点各分支节点的值,选择估值最大的分支节点 作为最佳解。 但是随着搜索深度的增加,博弈树的 节点数量成指数性增长。 在极大极小值算法的基础 上,Alpha⁃Beta 剪枝技术在搜索的过程中忽略了无 用的节点,并将其删除,不对其估值,删除无用节点 时不会造成信息丢失,不影响根节点各分支节点的 估值,提高了搜索速度[6] 。 在深层次的递归搜索中 广泛采用 Alpha⁃Beta 剪枝算法。 为了提高计算速 度,本文采用 Alpha⁃Beta 剪枝技术。 由于六子棋对弈规则的特殊性,如果只考虑单 个棋子对棋局的影响进行估值计算,而未考虑棋子 间的位置关系,肯定会影响棋局状态的评估效果,由 此产生了基于棋形的扫描方式[7⁃8] 。 常见的棋形主 要分为六连、长连、活五、眠五、死五、活四、眠四、死 四、活三、眠三、朦胧三、活二、眠二、朦胧二等[9] 。 文献[2]提出基于棋形的数据表示方法,数据结构 依赖于棋形,将棋局的数据表示和局面知识结合起 来,提高搜索效率。 基于棋形的扫描方式将棋子间的位置关系联系 起来,通过产生某种棋形来表示对整个棋局状态的 影响程度,更具有直观性,减少对单个棋子进行估值 的不稳定性;然而目前棋形是通过经验总结的,人为 因素影响很大,不排除还存在其他种类,这需要通过 大量实验来确定。 大部分六子棋的估值计算都是基 于棋形的扫描方式,但是由于棋形的判断要求很高, 常见的棋形种类较多,且每种棋形又存在多种落子 方式[10] ,由此文献[11] 提出“路” 的扫描方式。 所 谓“路”就在棋盘的水平、垂直或对角线上出现连续 6 点连成一线[11] 。 基于“路”扫描方式能有效降低棋形判断的复 杂度,通过“路”扫描方式的估值相对于通过棋形扫 描方式估值较为简单,实现方面也更加容易,并且搜 索时间较短。 文献[12]在传统的基于“路”的全局 扫描方式上采用自学习的方法自动调整估值函数的 参数,提高搜索精度。 文献[13]在应用 Alpha⁃Beta 剪枝搜索时引入并行计算,大幅度提高搜索效率。 “路”扫描方式的引入避免了精确判断棋形的 难题,减少了计算量;同时应用面向对象的思想,将 “路”的信息抽象成类,易于实现。 基于“路” 的扫 描方式解决了因棋形判断不准确而影响博弈水平的 问题,但是应用博弈树搜索时,在对每个子节点的扩 展时都需要对棋盘进行全局扫描。 受博弈竞赛时间 约束,搜索深度和宽度都有所限制,博弈水平也达不 到理想要求。 因此本文在博弈树生成子节点时将基 于“路”的全局扫描方式改进为局部扫描,并设计基 于局部“路”扫描方式的博弈树生成算法。 1 基于“路”的全局扫描方式 1.1 计算规则 K 子棋可用 connect( m,n,k,p,q) 表示[1 4 ] ,对弈 双方为黑方和白方,黑方先走。 connect( m,n,k,p,q) 的规则包括:1)棋盘的方格为 m行n 列,即含m × n 个 交叉点;2) 对弈时双方轮流落 p 颗棋子(根据六子棋 比赛黑方先手规则,第 1 次落 q 颗棋子);3) 在棋盘的 水平、垂直或对角线上先形成 k 连获胜。 若在规定时 间内双方均无法获胜,则判为平局。 K 子棋中“ 路” 的计算规则:1) 水平方向:m 行 ×(n - k + 1) 路 / 行,如图 1 中(a) 所示;2) 垂直 方向:n 列 × (m - k + 1) 路 / 列,类似于水平方向; 3) 左斜方向:由于 k 连需要 k 子连续相连,在左斜方 向前 k - 1 行不可能形成 k 连,故左斜方向路数为 (m -k + 1) 行 × (n - k + 1) 路 / 行,如图 1 中(b); 4) 右斜方向:(n - k + 1) 列 × (m - k + 1) 路 / 列, 类似于左斜方向。 六子棋是 K 子棋的一种[1 5 ] ,采用 19×19 方格 棋盘,可表示为 connect(19,19,6,2,1),总路数为 Nroad = ∑ 3 i = 0 Ndirect (i) (1) 式 中: Nroad 表 示 六 子 棋 全 局 扫 描 总 路 数, ·268· 智 能 系 统 学 报 第 10 卷

第2期 李学俊,等:六子棋中基于局部“路”扫描方式的博弈树生成算法 ·269. Ne()表示第i方向上的路数。根据式(I)可得, 2 六子棋19×19方格全局扫描的总路数为924。 基于“路”的局部扫描方式 012345678… 应用Alpha-Beta剪枝技术搜索时,效率和精确 1×××××X××××××××X××× 度是非常重要又相互影响的因素16]。文献[2]中 )××××X××××××××××××××, 3 XXXXX×XXXX×X×XXXXXx 指出棋局状态的变化均由新增的棋子引起,在棋局 4×××××××X××××X××××××, 中只有新增棋子的水平方向、垂直方向和对角线方 6X××××××××××××××××××, 7××××××××××××××××××× 向上的棋形发生变化,对其他位置棋形无影响。在 8××××x××××××××X×XX×X .××X×××X×××X×X×××XXX 基于“路”的扫描过程中,每步落子对棋局的影响是 :×××X×××XX×XX×XXXX×X ×X×××X×X×××××××××××, 由该两落子在水平方向、垂直方向和对角线方向上 ××××××××XX××XX××××X m-1×××××××××××××××××××, 的“路”所引起,与其他“路”没有关系,故本文在博 (a)水平方向扫描 弈树生成时,优化改进“路”的扫描方式。 012345678… 0×××××××X××××××××× 2.1计算规则 1××××圈X×××X××××X××× 假设在棋盘的(3,7)位置模拟一个落子,由图2 2X×X×××××××××XXXXX, 3×X■X×X××X XX X XXX 1(×××X××X××X×X×XXX 可得在水平方向有6路包含该落子,由此可得在局 6K××××××××××X××X×XX×. 部扫描方式下,每步落子所影响的路数计算如式 (5)所示。 8K××××××××××××××××××. K×××××××X××××××XX×× Vnan=Vait×N.nx N,he (5) K×XX×××X×××××××××××. (××XX×XX×XXX××XXXXx 式中:N表示局部扫描每步落子影响的路数, XXXXXXXxxXXxx×X×XXX, m-k×××××××××XX××XXX Ne表示每个方向所含的路数,Vm表示一个落子 (b)左斜方向扫描 所要扫描的方向数,N表示每步的落子数。 图1水平及左斜方向路数计算示例 012345678… 18 Fig.1 Road number of horizontal and left diagonal di- 1XX×XX×X×X×X×X××××X×, rection 2××××××X××××××××××XX. 1.2估值分析 .XXX0X××X×XX, :×XXXXXX×××××X××××××- 在“路”的信息表示中,设置n∈{0,1,2,3,4,5, ××××××××××××××××××× 18×××××××××××××××X××× 6}表示该路中相同颜色棋子的个数,设置c∈{'B' 图2局部扫描水平方向路数计算示例 '矿}表示路中棋子的颜色。若某路中含2种颜色棋 Fig.2 Road number of horizontal direction by the lo- 子,表示该路不可能成为六连,则初始值不变。 cal-road scanning method 当某路中c为已方棋子颜色时分配不同的价 由式(5)可得,一般情况下局部扫描的总路数 值,计算分配价值公式为 为:6路/方向×4方向/落子×2落子=48路,大大小 V=f(n) (2) 于全局扫描的总路数924。局部扫描棋局估值V' 式中:Vm表示分配的价值,n越大表明己方在该路 即落子后棋盘局部扫描估值V'减去落子前棋盘 越容易形成六连,则分配的价值越大。 局部扫描估值V,可表达为 当某路中c为对方棋子颜色时分配不同的威胁 V'total V'sther V'pre (6) 值,计算威胁值公式为 2.2估值分析 Vuhreat =g(n) (3) 局部扫描方式本质上和全局扫描方式的不同在 式中:V山em表示分配的威胁值,n越大表明对方在 于对每个子节点进行扩展时都要应用“路”进行局部 该路越容易形成六连,则分配的威胁值越大。 扫描而不是全局扫描,它们的估值存在一定的联系。 1)落子前落子点位置影响的局部扫描的“路” 全局扫描估值可用己方所有“路”的价值之和 估值V'与除局部扫描以外的“路”估值V”之和 减去对方所有“路”的威胁值之和表示。全局扫描 相当于落子前棋盘全局扫描估值V,可表达为 棋局估值V可看作是每步落子后对当前棋局的 V'pre Vpre Vpre (7) 影响程度大小,即落子后棋盘全局扫描估值V减 2)落子后落子点位置影响的局部扫描的“路” 去落子前棋盘全局扫描估值V,可表达为 估值V”与除局部扫描以外的“路”估值V"之和 Viotal Vater -Vpre (4) 相当于落子后棋盘全局扫描估值V,可表达为
Ndirect (i) 表示第 i 方向上的路数。 根据式(1)可得, 六子棋 19×19 方格全局扫描的总路数为 924。 图 1 水平及左斜方向路数计算示例 Fig.1 Road number of horizontal and left diagonal di⁃ rection 1.2 估值分析 在“路”的信息表示中,设置 n ∈ {0,1,2,3,4,5, 6} 表示该路中相同颜色棋子的个数,设置 c ∈ {′B′, ′W′} 表示路中棋子的颜色。 若某路中含 2 种颜色棋 子,表示该路不可能成为六连,则初始值不变。 当某路中 c 为已方棋子颜色时分配不同的价 值,计算分配价值公式为 Vown = f(n) (2) 式中: Vown 表示分配的价值, n 越大表明己方在该路 越容易形成六连,则分配的价值越大。 当某路中 c 为对方棋子颜色时分配不同的威胁 值,计算威胁值公式为 Vthreat = g(n) (3) 式中: Vthreat 表示分配的威胁值, n 越大表明对方在 该路越容易形成六连,则分配的威胁值越大。 全局扫描估值可用己方所有“路” 的价值之和 减去对方所有“路”的威胁值之和表示。 全局扫描 棋局估值 Vtotal 可看作是每步落子后对当前棋局的 影响程度大小,即落子后棋盘全局扫描估值 Vafter 减 去落子前棋盘全局扫描估值 Vpre ,可表达为 Vtotal = Vafter - Vpre (4) 2 基于“路”的局部扫描方式 应用 Alpha⁃Beta 剪枝技术搜索时,效率和精确 度是非常重要又相互影响的因素[1 6 ] 。 文献[2] 中 指出棋局状态的变化均由新增的棋子引起,在棋局 中只有新增棋子的水平方向、垂直方向和对角线方 向上的棋形发生变化,对其他位置棋形无影响。 在 基于“路”的扫描过程中,每步落子对棋局的影响是 由该两落子在水平方向、垂直方向和对角线方向上 的“路”所引起,与其他“路”没有关系,故本文在博 弈树生成时,优化改进“路”的扫描方式。 2.1 计算规则 假设在棋盘的(3,7)位置模拟一个落子,由图 2 可得在水平方向有 6 路包含该落子,由此可得在局 部扫描方式下,每步落子所影响的路数计算如式 (5)所示。 Npart = Ndirect × Nscan × Nchess (5) 式中: Npart 表示局部扫描每步落子影响的路数, Ndirect 表示每个方向所含的路数, Nscan 表示一个落子 所要扫描的方向数, Nchess 表示每步的落子数。 图 2 局部扫描水平方向路数计算示例 Fig.2 Road number of horizontal direction by the lo⁃ cal⁃road scanning method 由式(5)可得,一般情况下局部扫描的总路数 为:6 路/ 方向×4 方向/ 落子×2 落子 = 48 路,大大小 于全局扫描的总路数 924。 局部扫描棋局估值 V′total 即落子后棋盘局部扫描估值 V′after 减去落子前棋盘 局部扫描估值 V′pre ,可表达为 V′total = V′after - V′pre (6) 2.2 估值分析 局部扫描方式本质上和全局扫描方式的不同在 于对每个子节点进行扩展时都要应用“路”进行局部 扫描而不是全局扫描,它们的估值存在一定的联系。 1)落子前落子点位置影响的局部扫描的“路” 估值 V′pre 与除局部扫描以外的“路”估值 V″pre 之和 相当于落子前棋盘全局扫描估值 Vpre ,可表达为 V′pre + V″pre = Vpre (7) 2)落子后落子点位置影响的局部扫描的“路” 估值 V′after 与除局部扫描以外的“路”估值 V″after 之和 相当于落子后棋盘全局扫描估值 Vafter ,可表达为 第 2 期 李学俊,等: 六子棋中基于局部“路”扫描方式的博弈树生成算法 ·269·

·270. 智能系统学报 第10卷 V'afet V"ater Vater (8) 前局部扫描估值 3)由于每步落子不会对局部扫描以外的“路” 7)SimulateMove():/模拟落子 估值产生影响,即落子后除局部扫描以外的“路”估 8)scanPart(ListPoints[i].Point,ListPoints[j]. 值。等于落子前除局部扫描以外的“路”估值 Point);/落子后局部扫描 ”,表达为 9)Part_after Value=Caculate():/计算模拟落 V"hr=广"e (9) 子后局部扫描估值 所以,局部扫描的棋局估值为 10)Value=Part_afterValue-Part_preValue; V'total V'sfter V'pre Vster Vpre 11)RestoreMove();//撤销落子 (V'sher V"ahe)-(V'pre V"pre) (10) 12)AddListWay ListPoints[i ]Point,ListPoints 由式(10)可以看出,局部扫描方式和全局扫描 j].Point,Value); 方式的棋盘估值相同,并没有降低精确度,因此在博 13)} 弈树生成时,本文将棋盘扫描方式由全局扫描改进 14)GetList Way(ListWay,Width); 为局部扫描,忽略无用扫描,以提高搜索速度。 4 实验 3局部扫描方式的博弈树生成算法 4.1实验环境 局部扫描方式的博弈树生成算法主要用于子节 基于上述六子棋搜索策略,本文设计并实现了 点的扩展过程。因为搜索的宽度是有限的,根节点 六子棋博弈系统Dragon World(龙行天下)-人机对 递归向下搜索时,先采用局部扫描方式扩展子节点 弈平台。该系统采用C#语言开发,操作系统为 并进行估值,并通过排序选择估值排名靠前的 Windows7,硬件环境为联想(G490)CPU、2.60GHZ Wdh个节点继续递归向下搜索,删除其他不进行 的nter处理器和4G内存。 递归搜索的节点。为了更方便地应用博弈搜索策 4.2实验与分析 略,将“2步”落子并作“一步”,对模拟的2步落子 为比较不同的扫描方式,本文从搜索效率和博 进行综合估值,保证搜索效率和博弈水平。基于局 弈水平2个角度进行实验对比。通过搜索效率的实 部扫描方式的博弈树生成算法伪代码如下。 验,分析不同深度和宽度对搜索效率的影响。通过 基于局部扫描的博弈树生成算法中,输入模拟 博弈水平的实验,在严格遵循竞赛时间要求的前提 落子的棋子颜色Color及搜索宽度Widh,输出估值 下,分析同等条件下不同搜索深度和宽度对博弈水 排名前Width的落子组合点。 平的影响。实验中每局对弈时间不超过l5min。 本文的六子棋搜索算法采用Alpha-Beta剪枝技 表1价值与威胁值分配 术实现,设置深度为Depth,宽度为Width。对弈过 Table 1 The distribution of the value and threat value 程中,根据当前棋局状态扩展子节点时,采用基于局 路数 己方路的价值 对方路的威胁值 部扫描的博弈树生成算法对所有可以进行扩展的子 6路 1000000 1000000 节点进行估值,选择估值为前Widh名的子节点继 5路 200 6000 续扩展,直至扩展深度为Depth为止。通过对叶子 节点估值,倒推计算根部各分支节点的估值,选择最 4路 200 6000 大值节点对应的落子方式为最佳解。 3路 40 50 /*Input:Color,Width Output:listWay(估值排 2路 20 25 名前Widh的2步落子组合)*/ 1路 1 1)Localscanning(int Color,int Width) 2)AddMovePoints(ListPoints);/计算模拟移动 4.2.1搜索效率实验 的落子位置 搜索效率包括深度和宽度2个方面。通过深度 3)for(i=0;i<ListPoints.Count-1;i++) 实验,分析同等宽度情况下不同搜索深度对搜索效 4)for(j=i+1;j<ListPoints.Count;j++) 率的影响:通过宽度实验,分析同等深度情况下不同 5)scanPart(ListPoints[i ]Point,ListPoints[j]. 搜索宽度对搜索效率的影响。 Point);//落子前局部扫描 设置Widh=10,采用深度为3、4、5时,全局扫 6)Part_pre Value=Caculate();/计算模拟落子 描和局部扫描时间进行对比实验,各对弈100局,每
V′after + V″after = Vafter (8) 3)由于每步落子不会对局部扫描以外的“路” 估值产生影响,即落子后除局部扫描以外的“路”估 值 V″after 等于落子前除局部扫描以外的“路” 估值 V″pre ,表达为 V″after = V″pre (9) 所以,局部扫描的棋局估值为 V′total = V′after - V′pre = Vafter - Vpre = V′after + V″after ( ) - V′pre + V″pre ( ) (10) 由式(10)可以看出,局部扫描方式和全局扫描 方式的棋盘估值相同,并没有降低精确度,因此在博 弈树生成时,本文将棋盘扫描方式由全局扫描改进 为局部扫描,忽略无用扫描,以提高搜索速度。 3 局部扫描方式的博弈树生成算法 局部扫描方式的博弈树生成算法主要用于子节 点的扩展过程。 因为搜索的宽度是有限的,根节点 递归向下搜索时,先采用局部扫描方式扩展子节点 并进行 估 值, 并 通 过 排 序 选 择 估 值 排 名 靠 前 的 Width 个节点继续递归向下搜索,删除其他不进行 递归搜索的节点。 为了更方便地应用博弈搜索策 略,将“2 步”落子并作“一步”,对模拟的 2 步落子 进行综合估值,保证搜索效率和博弈水平。 基于局 部扫描方式的博弈树生成算法伪代码如下。 基于局部扫描的博弈树生成算法中,输入模拟 落子的棋子颜色 Color 及搜索宽度 Width,输出估值 排名前 Width 的落子组合点。 本文的六子棋搜索算法采用 Alpha⁃Beta 剪枝技 术实现,设置深度为 Depth,宽度为 Width。 对弈过 程中,根据当前棋局状态扩展子节点时,采用基于局 部扫描的博弈树生成算法对所有可以进行扩展的子 节点进行估值,选择估值为前 Width 名的子节点继 续扩展,直至扩展深度为 Depth 为止。 通过对叶子 节点估值,倒推计算根部各分支节点的估值,选择最 大值节点对应的落子方式为最佳解。 / ∗Input:Color,Width Output:listWay (估值排 名前 Width 的 2 步落子组合)∗/ 1) Localscanning(int Color,int Width){ 2)AddMovePoints(ListPoints); / / 计算模拟移动 的落子位置 3)for( i = 0; i <ListPoints.Count-1; i ++) 4)for(j = i +1; j <ListPoints.Count; j ++){ 5)scanPart(ListPoints[ i ].Point,ListPoints[ j ]. Point); / / 落子前局部扫描 6)Part_preValue = Caculate( ); / / 计算模拟落子 前局部扫描估值 7)SimulateMove(); / / 模拟落子 8)scanPart(ListPoints[ i ].Point,ListPoints[ j ]. Point); / / 落子后局部扫描 9)Part_afterValue = Caculate( ); / / 计算模拟落 子后局部扫描估值 10)Value = Part_afterValue-Part_preValue; 11)RestoreMove(); / / 撤销落子 12)AddListWay(ListPoints[ i ].Point,ListPoints [ j ].Point,Value); 13)} 14)GetListWay(ListWay,Width); 4 实验 4.1 实验环境 基于上述六子棋搜索策略,本文设计并实现了 六子棋博弈系统 DragonWorld(龙行天下) -人机对 弈平台。 该系统采用 C # 语言开发, 操作系统为 Windows 7,硬件环境为联想(G490) CPU、2.60 GHZ 的 Inter 处理器和 4 G 内存。 4.2 实验与分析 为比较不同的扫描方式,本文从搜索效率和博 弈水平 2 个角度进行实验对比。 通过搜索效率的实 验,分析不同深度和宽度对搜索效率的影响。 通过 博弈水平的实验,在严格遵循竞赛时间要求的前提 下,分析同等条件下不同搜索深度和宽度对博弈水 平的影响。 实验中每局对弈时间不超过 15 min。 表 1 价值与威胁值分配 Table 1 The distribution of the value and threat value 路数 己方路的价值 对方路的威胁值 6 路 1 000 000 1 000 000 5 路 200 6 000 4 路 200 6 000 3 路 40 50 2 路 20 25 1 路 1 1 4.2.1 搜索效率实验 搜索效率包括深度和宽度 2 个方面。 通过深度 实验,分析同等宽度情况下不同搜索深度对搜索效 率的影响;通过宽度实验,分析同等深度情况下不同 搜索宽度对搜索效率的影响。 设置 Width = 10,采用深度为 3、4、5 时,全局扫 描和局部扫描时间进行对比实验,各对弈 100 局,每 ·270· 智 能 系 统 学 报 第 10 卷
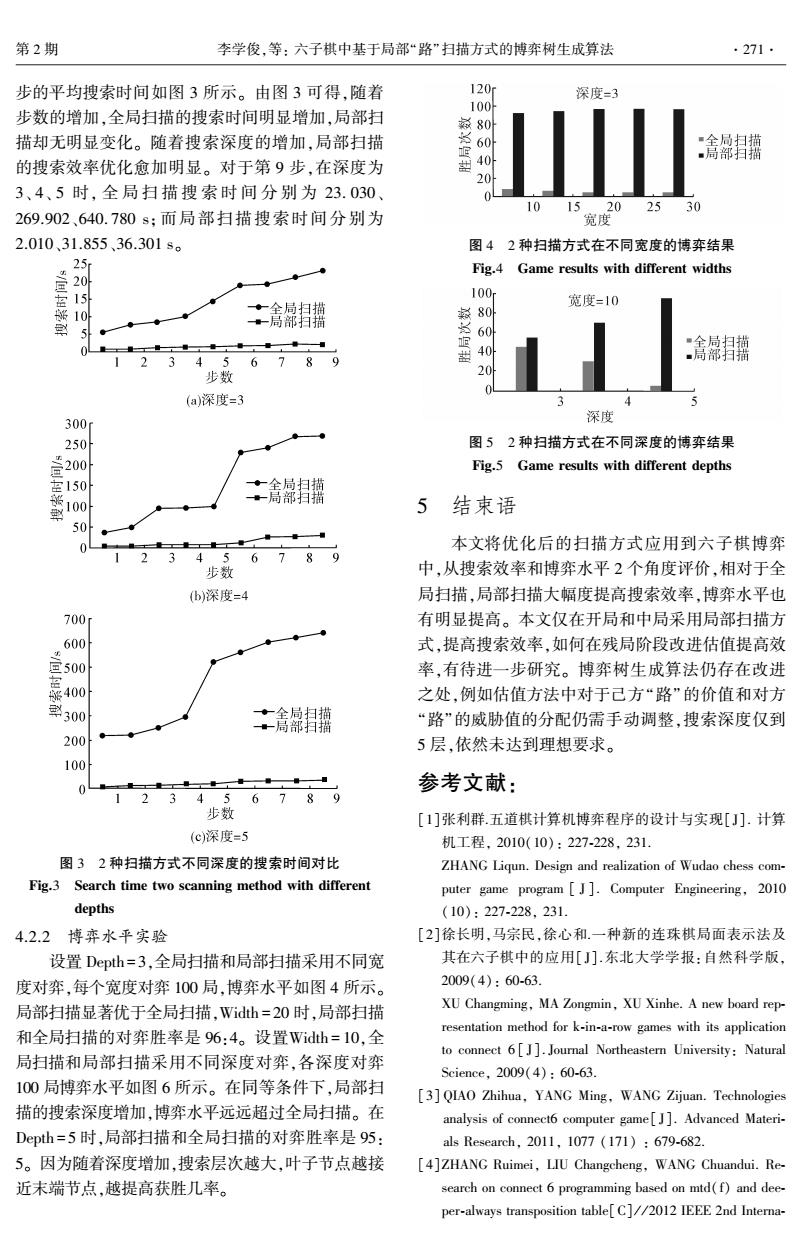
第2期 李学俊,等:六子棋中基于局部“路”扫描方式的博弈树生成算法 .271. 步的平均搜索时间如图3所示。由图3可得,随着 120- 深度-3 步数的增加,全局扫描的搜索时间明显增加,局部扫 100 描却无明显变化。随着搜索深度的增加,局部扫描 的搜索效率优化愈加明显。对于第9步,在深度为 60100 3、4、5时,全局扫描搜索时间分别为23.030、 1015202530 269.902、640.780s;而局部扫描搜索时间分别为 宽度 2.010、31.855、36.301s。 图42种扫描方式在不同宽度的博弈结果 Fig.4 Game results with different widths 20 100r 宽度=10 一全局扫描 一高部扫描 0量工工1 000 “舍局扫描 123456789 .高部扫揣 步数 (a)深度=3 300 深度 0 图52种扫描方式在不同深度的博弈结果 20 Fig.5 Game results with different depths ·全局扫描 。一局部扫描 5 结束语 04 本文将优化后的扫描方式应用到六子棋博弈 3 456789 步数 中,从搜索效率和博弈水平2个角度评价,相对于全 ()深度=4 局扫描,局部扫描大幅度提高搜索效率,博弈水平也 700 有明显提高。本文仅在开局和中局采用局部扫描方 00 式,提高搜索效率,如何在残局阶段改进估值提高效 意50 率,有待进一步研究。博弈树生成算法仍存在改进 之处,例如估值方法中对于己方“路”的价值和对方 300 ◆全局扫描 一局部扫描 “路”的威胁值的分配仍需手动调整,搜索深度仅到 200 5层,依然未达到理想要求。 100 参考文献: 23456789 步数 [1]张利群.五道棋计算机博弈程序的设计与实现[J].计算 (c)深度=5 机工程,2010(10):227-228,231. 图32种扫描方式不同深度的搜索时间对比 ZHANG Liqun.Design and realization of Wudao chess com- Fig.3 Search time two scanning method with different puter game program [J].Computer Engineering,2010 depths (10):227-228.231 4.2.2博弈水平实验 [2]徐长明,马宗民,徐心和.一种新的连珠棋局面表示法及 设置Depth=3,全局扫描和局部扫描采用不同宽 其在六子棋中的应用[J].东北大学学报:自然科学版, 度对弈,每个宽度对弈100局,博弈水平如图4所示。 2009(4):60-63. 局部扫描显著优于全局扫描,Widh=20时,局部扫描 XU Changming,MA Zongmin,XU Xinhe.A new board rep- 和全局扫描的对弈胜率是96:4。设置Widh=10,全 resentation method for k-in-a-row games with its application to connect 6[J].Journal Northeastern University:Natural 局扫描和局部扫描采用不同深度对弈,各深度对弈 Science,,2009(4):60-63. 100局博弈水平如图6所示。在同等条件下,局部扫 [3]QIAO Zhihua,YANG Ming,WANG Zijuan.Technologies 描的搜索深度增加,博弈水平远远超过全局扫描。在 analysis of connect6 computer game[J].Advanced Materi- Depth=5时,局部扫描和全局扫描的对弈胜率是95: als Research,2011,1077(171):679-682. 5。因为随着深度增加,搜索层次越大,叶子节点越接 [4]ZHANG Ruimei,LIU Changcheng,WANG Chuandui.Re- 近末端节点,越提高获胜几率。 search on connect 6 programming based on mtd(f)and dee- per-always transposition table[C]//2012 IEEE 2nd Interna-
步的平均搜索时间如图 3 所示。 由图 3 可得,随着 步数的增加,全局扫描的搜索时间明显增加,局部扫 描却无明显变化。 随着搜索深度的增加,局部扫描 的搜索效率优化愈加明显。 对于第 9 步,在深度为 3、 4、 5 时, 全 局 扫 描 搜 索 时 间 分 别 为 23. 030、 269.902、640. 780 s;而局部扫描搜索时间分别为 2.010、31.855、36.301 s。 图 3 2 种扫描方式不同深度的搜索时间对比 Fig.3 Search time two scanning method with different depths 4.2.2 博弈水平实验 设置 Depth = 3,全局扫描和局部扫描采用不同宽 度对弈,每个宽度对弈 100 局,博弈水平如图 4 所示。 局部扫描显著优于全局扫描,Width = 20 时,局部扫描 和全局扫描的对弈胜率是 96:4。 设置Width = 10,全 局扫描和局部扫描采用不同深度对弈,各深度对弈 100 局博弈水平如图 6 所示。 在同等条件下,局部扫 描的搜索深度增加,博弈水平远远超过全局扫描。 在 Depth = 5 时,局部扫描和全局扫描的对弈胜率是 95: 5。 因为随着深度增加,搜索层次越大,叶子节点越接 近末端节点,越提高获胜几率。 图 4 2 种扫描方式在不同宽度的博弈结果 Fig.4 Game results with different widths 图 5 2 种扫描方式在不同深度的博弈结果 Fig.5 Game results with different depths 5 结束语 本文将优化后的扫描方式应用到六子棋博弈 中,从搜索效率和博弈水平 2 个角度评价,相对于全 局扫描,局部扫描大幅度提高搜索效率,博弈水平也 有明显提高。 本文仅在开局和中局采用局部扫描方 式,提高搜索效率,如何在残局阶段改进估值提高效 率,有待进一步研究。 博弈树生成算法仍存在改进 之处,例如估值方法中对于己方“路”的价值和对方 “路”的威胁值的分配仍需手动调整,搜索深度仅到 5 层,依然未达到理想要求。 参考文献: [1]张利群.五道棋计算机博弈程序的设计与实现[ J]. 计算 机工程, 2010(10): 227⁃228, 231. ZHANG Liqun. Design and realization of Wudao chess com⁃ puter game program [ J ]. Computer Engineering, 2010 (10): 227⁃228, 231. [2]徐长明,马宗民,徐心和.一种新的连珠棋局面表示法及 其在六子棋中的应用[ J].东北大学学报:自然科学版, 2009(4): 60⁃63. XU Changming, MA Zongmin, XU Xinhe. A new board rep⁃ resentation method for k⁃in⁃a⁃row games with its application to connect 6 [ J]. Journal Northeastern University: Natural Science, 2009(4): 60⁃63. [3] QIAO Zhihua, YANG Ming, WANG Zijuan. Technologies analysis of connect6 computer game[ J]. Advanced Materi⁃ als Research, 2011, 1077 (171) : 679⁃682. [4]ZHANG Ruimei, LIU Changcheng, WANG Chuandui. Re⁃ search on connect 6 programming based on mtd(f) and dee⁃ per⁃always transposition table[C] / / 2012 IEEE 2nd Interna⁃ 第 2 期 李学俊,等: 六子棋中基于局部“路”扫描方式的博弈树生成算法 ·271·

.272. 智能系统学报 第10卷 tional Conference on Cloud Computing and Intelligence Sys- XU Changming,MA Zongmin,XU Xinhe.Study of tempo- tems.[S.l.],2012:254-255. ral difference learning in computer games[].Computer [5]徐长明.基于连珠模式的六子棋机器博弈关键技术研究 Science,2010(8):225-229. [D].沈阳:东北大学,2010:15-36. [13]徐心和,邓志立,王骄,等.机器博弈研究面临的各种 XU Changming.Research on key technologies of connection- 挑战[J].智能系统学报,2008,3(4):10-15. pattern based computer connect 6[D].Shenyang:North- XU Xinhe,DENG Zhili,WANG Jiao,et al.Challenging eastern University,2010:15-36. issues facing computer game research[J].CAAI Transac- [6]KNUTH D E,MOORE R W.An analysis of alpha-beta tions on Intelligent Systems,2008,3(4):10-15. pruning[J].Artificial Intelligence,1975,6(4):293-326. [14]闵文杰.六子棋计算机博弈关键技术研究[D].重庆: [7]李翠珠.六子棋计算机博弈系统的研究与实现[D].重 重庆交通大学,2010:12-18. 庆:重庆理工大学,2010:43-46. MIN Wenjie.Research on the key technologies of the con- LI Cuizhu.Research and Implementation of the system of nect 6 computer game[D].Chongqing:Chongqing Jiaotong connect 6 game [D].Chongqing:Chongqing University of University,2010:12-18. Technology,2010:43-46. [15]MARTIN K,SVEN S,RAINER H.Improved tree-based [8]张颖六子棋启发式搜索算法的优化与设计[J].西北师 strategies for a connect 6 threat-based hardware design 范大学学报:自然科学版,2008(4):31-36,58. [C]//2013 IEEE Pacific Rim Conference on Communica- ZHANG Ying.Optimization and design of connect6 heuristic tions,Computers and Signal Processing PACRIM). searching algorithm[J].Journal of Northwest Normal Uni- [S.1.],2013:32-36. versity:Natural Science,2008(4):31-36,58. [16]张明亮,吴俊,李凡长.五子棋机器博弈系统评估函数的 [9]黄继平,苗华,张栋用遗传算法实现六子棋评估函数参 设计[J].计算机应用,2012(7):189-192,210. 数优化[J].重庆工学院学报:自然科学版,2009(11): ZHANG Mingliang,WU Jun,LI Fanchang.Design of eval- 91-95. uation function for computer gobang game system[J].Jour- HUANG Jiping,MIAO Hua,ZHANG Dong.Optimizing the nal of Computer Applications,2012(7):189-192,210. evaluation function parameters of connect6 with genetic algo- 作者简介: rithms[J].Journal of Chongqing Institute of Technology: 李学俊,男,1976年生,副教授,中 Natural Science,2009(11):91-95. 国人工智能学会机器博弈专业委员会 [10]陈光年.基于智能算法的六子棋博弈行为选择的应用研 理事,主要研究方向为智能软件、云工 究[D].重庆:重庆理工大学,2010:20-25. 作流。 CHEN Guangnian.The research and application on the be- havior election of connect 6 based on intelligent algorithms [D].Chongqing:Chongqing University of Technology, 王小龙,男,1989年生,硕士,主要 2010:20-25. [11]张小川,陈光年,张世强,等.六子棋博弈的评估函数 研究方向为机器博弈。 [J].重庆理工大学学报:自然科学版,2010(2):68 72. ZHANG Xiaochuan,CHEN Guangnian,ZHANG Shiqiang. Research on evaluation functions for computer game of con- 吴蕾,女,1978年生,讲师,博士研 nect6[J].Journal of Chongqing University of Technology: 究生,中国人工智能学会机器博弈专业 Natural Science,2010(2):68-72. 委员会理事,主要研究方向为机器博 [12]徐长明,马宗民,徐心和,等.面向机器博弈的即时差 分学习研究[J].计算机科学,2010(8):225-229. 弈,软件测试
tional Conference on Cloud Computing and Intelligence Sys⁃ tems. [S.l.], 2012: 254⁃255. [5]徐长明.基于连珠模式的六子棋机器博弈关键技术研究 [D]. 沈阳: 东北大学, 2010: 15⁃36. XU Changming. Research on key technologies of connection⁃ pattern based computer connect 6 [ D]. Shenyang: North⁃ eastern University, 2010: 15⁃36. [6] KNUTH D E, MOORE R W. An analysis of alpha⁃beta pruning[J]. Artificial Intelligence, 1975, 6(4): 293⁃326. [7]李翠珠.六子棋计算机博弈系统的研究与实现[D]. 重 庆: 重庆理工大学, 2010: 43⁃46. LI Cuizhu. Research and Implementation of the system of connect 6 game [D]. Chongqing: Chongqing University of Technology, 2010: 43⁃46. [8]张颖.六子棋启发式搜索算法的优化与设计[ J]. 西北师 范大学学报: 自然科学版, 2008(4): 31⁃36, 58. ZHANG Ying. Optimization and design of connect6 heuristic searching algorithm[ J]. Journal of Northwest Normal Uni⁃ versity: Natural Science, 2008(4): 31⁃36, 58. [9]黄继平,苗华,张栋.用遗传算法实现六子棋评估函数参 数优化[J]. 重庆工学院学报: 自然科学版, 2009(11): 91⁃95. HUANG Jiping, MIAO Hua, ZHANG Dong. Optimizing the evaluation function parameters of connect6 with genetic algo⁃ rithms [ J]. Journal of Chongqing Institute of Technology: Natural Science, 2009(11): 91⁃95. [10]陈光年.基于智能算法的六子棋博弈行为选择的应用研 究[D]. 重庆: 重庆理工大学, 2010: 20⁃25. CHEN Guangnian. The research and application on the be⁃ havior election of connect 6 based on intelligent algorithms [D]. Chongqing: Chongqing University of Technology, 2010: 20⁃25. [11]张小川, 陈光年, 张世强, 等.六子棋博弈的评估函数 [J]. 重庆理工大学学报: 自然科学版, 2010( 2): 68⁃ 72. ZHANG Xiaochuan, CHEN Guangnian, ZHANG Shiqiang. Research on evaluation functions for computer game of con⁃ nect6[J]. Journal of Chongqing University of Technology: Natural Science, 2010(2): 68⁃72. [12]徐长明, 马宗民, 徐心和, 等. 面向机器博弈的即时差 分学习研究[J]. 计算机科学, 2010(8): 225⁃229. XU Changming, MA Zongmin, XU Xinhe. Study of tempo⁃ ral difference learning in computer games [ J]. Computer Science, 2010(8): 225⁃229. [13]徐心和, 邓志立, 王骄, 等.机器博弈研究面临的各种 挑战[J]. 智能系统学报, 2008, 3(4): 10⁃15. XU Xinhe, DENG Zhili, WANG Jiao, et al. Challenging issues facing computer game research[ J]. CAAI Transac⁃ tions on Intelligent Systems, 2008, 3(4): 10⁃15. [14]闵文杰. 六子棋计算机博弈关键技术研究[D]. 重庆: 重庆交通大学, 2010: 12⁃18. MIN Wenjie. Research on the key technologies of the con⁃ nect 6 computer game[D]. Chongqing: Chongqing Jiaotong University, 2010: 12⁃18. [15] MARTIN K, SVEN S, RAINER H. Improved tree⁃based strategies for a connect 6 threat⁃based hardware design [C] / / 2013 IEEE Pacific Rim Conference on Communica⁃ tions, Computers and Signal Processing ( PACRIM ). [S.l.], 2013: 32⁃36. [16]张明亮,吴俊,李凡长.五子棋机器博弈系统评估函数的 设计[J]. 计算机应用, 2012(7): 189⁃192, 210. ZHANG Mingliang, WU Jun, LI Fanchang. Design of eval⁃ uation function for computer gobang game system[J]. Jour⁃ nal of Computer Applications, 2012(7): 189⁃192, 210. 作者简介: 李学俊,男,1976 年生,副教授,中 国人工智能学会机器博弈专业委员会 理事,主要研究方向为智能软件、云工 作流。 王小龙,男,1989 年生,硕士,主要 研究方向为机器博弈。 吴蕾,女,1978 年生,讲师,博士研 究生,中国人工智能学会机器博弈专业 委员会理事,主要研究方向为机器博 弈,软件测试。 ·272· 智 能 系 统 学 报 第 10 卷