
第9卷第5期 智能系统学报 Vol.9 No.5 2014年10月 CAAI Transactions on Intelligent Systems 0ct.2014 D0:10.3969/j.issn.1673-4785.201305002 集对分析联系数在黑启动vague集决策中的应用研究 赵玉铃,张廉 (浙江水利水电学院,浙江杭州310018) 摘要:vagu集本质上是一种含有不确定性的模糊集,应用时需要做不确定性分析。为此,把集对分析联系数应用 于黑启动vague集决策之中。首先,把用vague集表示的专家权重,指标权重与指标值都改写成联系数的形式,得出 基于联系数的黑启动vgu集决策模型,再对模型的计算结果作不确定性分析,考察不确定性条件下的各方案排序 变化,选出最优方案。实例应用表明,文中所提方法能有效解决用vagu集表示的评价指标之间存在关联性和不确 定性的黑启动多方案选优问题,思路清晰,算法简明,便于现场决策应用。 关键词:黑启动决策;vgue集;指标关联性;不确定性;联系数;集对分析 中图分类号:TM711文献标志码:A文章编号:1673-4785(2014)05-0632-09 中文引用格式:赵玉铃,张廉.集对分析联系数在黑启动vgue集决策中的应用研究[J].智能系统学报,2014,9(5):632-640. 英文引用格式:ZHAO Yuling,ZHANG Lian..Application of the set--pair analysis connection number in decision-making of black- start vague set[J].CAAI Transactions on Intelligent Systems,2014,9(5):632-640. Application of the set-pair analysis connection number in decision-making of black-start vague set ZHAO Yuling,ZHANG Lian (Zhejiang University of Water Resources and Electric Power,Hangzhou 310018,China) Abstract:A vague set is a kind of fuzzy set that contains uncertainty.So uncertainty analysis is required in the ap- plication of it.To solve this problem,the proposed decision-making method of a black-start vague set is based on connection number analysis of set-pair.First,rewrite the expert weights,index weights and targeted values repre- sented by vague sets into the connection number form.Next,obtain the decision model of a vague set for black-start based on connection number,analyze the uncertainty of the model calculations,study the changes in the ranking of each project in conditions of uncertainty and select the optimal project.Practical application shows that the method can deal with the problem of optimizing black-start schemes of the correlation and uncertainty in the selected evalu- ation indexes effectively and clearly.It is simple in algorithm and convenient to make decision on spot. Keywords:black-start decision;vague set;correlation index;uncertainty;connection number;set-pair analysis 现代社会中,电力系统发生突发性的停电事故 杂的事情,快速优选出合理的黑启动方案有助于加 不仅会导致巨大的经济损失,也可能引发社会问题。 速系统的恢复3]。为此,文献[4]提出基于分层案 因此,系统和深入地研究停电后的电力系统快速恢 例推理的黑启动决策方法,文献[5]采用基于数据 复,具有重大理论意义和现实意义[2。 包络分析的层次法评估黑启动决策方案。基于黑启 黑启动是电力系统全部停电后迅速恢复供电的 动决策方案中指标及其权重以及参与决策的专家知 方式。对现代大型电力系统而言,黑启动是一件复 识存在不确定性的问题,文献[6]把直觉模糊集用 于黑启动群决策一致性分析与优化,文献[7]不仅 收稿日期:2013-05-02.网络出版日期: 基金项目:浙江省自然科学基金资助项目(Y505360). 把vague理论用于指标间存在关联性时的黑启动决 通信作者:赵玉铃.E-mail:djs0805@126.com. 策研究,而且还考虑了参与决策的专家间也存在关
第 9 卷第 5 期 智 能 系 统 学 报 Vol.9 №.5 2014 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2014 DOI:10.3969 / j.issn.1673⁃4785.201305002 集对分析联系数在黑启动 vague 集决策中的应用研究 赵玉铃,张廉 (浙江水利水电学院,浙江 杭州 310018) 摘 要:vague 集本质上是一种含有不确定性的模糊集,应用时需要做不确定性分析。 为此,把集对分析联系数应用 于黑启动 vague 集决策之中。 首先,把用 vague 集表示的专家权重、指标权重与指标值都改写成联系数的形式,得出 基于联系数的黑启动 vague 集决策模型,再对模型的计算结果作不确定性分析,考察不确定性条件下的各方案排序 变化,选出最优方案。 实例应用表明,文中所提方法能有效解决用 vague 集表示的评价指标之间存在关联性和不确 定性的黑启动多方案选优问题,思路清晰,算法简明,便于现场决策应用。 关键词:黑启动决策;vague 集;指标关联性;不确定性;联系数;集对分析 中图分类号: TM711 文献标志码:A 文章编号:1673⁃4785(2014)05⁃0632⁃09 中文引用格式:赵玉铃,张廉. 集对分析联系数在黑启动 vague 集决策中的应用研究[J]. 智能系统学报, 2014, 9(5): 632⁃640. 英文引用格式:ZHAO Yuling,ZHANG Lian. Application of the set⁃pair analysis connection number in decision⁃making of black⁃ start vague set[J]. CAAI Transactions on Intelligent Systems, 2014, 9(5): 632⁃640. Application of the set⁃pair analysis connection number in decision⁃making of black⁃start vague set ZHAO Yuling,ZHANG Lian (Zhejiang University of Water Resources and Electric Power, Hangzhou 310018, China) Abstract:A vague set is a kind of fuzzy set that contains uncertainty. So uncertainty analysis is required in the ap⁃ plication of it. To solve this problem, the proposed decision⁃making method of a black⁃start vague set is based on connection number analysis of set⁃pair. First, rewrite the expert weights, index weights and targeted values repre⁃ sented by vague sets into the connection number form. Next, obtain the decision model of a vague set for black⁃start based on connection number, analyze the uncertainty of the model calculations, study the changes in the ranking of each project in conditions of uncertainty and select the optimal project. Practical application shows that the method can deal with the problem of optimizing black⁃start schemes of the correlation and uncertainty in the selected evalu⁃ ation indexes effectively and clearly. It is simple in algorithm and convenient to make decision on spot. Keywords:black⁃start decision; vague set; correlation index; uncertainty; connection number; set⁃pair analysis 收稿日期:2013⁃05⁃02. 网络出版日期:. 基金项目:浙江省自然科学基金资助项目(Y505360). 通信作者:赵玉铃. E⁃mail:dzjs0805@ 126.com. 现代社会中,电力系统发生突发性的停电事故 不仅会导致巨大的经济损失,也可能引发社会问题。 因此,系统和深入地研究停电后的电力系统快速恢 复,具有重大理论意义和现实意义[ 1⁃2] 。 黑启动是电力系统全部停电后迅速恢复供电的 方式。 对现代大型电力系统而言,黑启动是一件复 杂的事情,快速优选出合理的黑启动方案有助于加 速系统的恢复[3 ] 。 为此,文献[4]提出基于分层案 例推理的黑启动决策方法,文献[5]采用基于数据 包络分析的层次法评估黑启动决策方案。 基于黑启 动决策方案中指标及其权重以及参与决策的专家知 识存在不确定性的问题,文献[6]把直觉模糊集用 于黑启动群决策一致性分析与优化,文献[7] 不仅 把 vague 理论用于指标间存在关联性时的黑启动决 策研究,而且还考虑了参与决策的专家间也存在关

第5期 赵玉铃,等:集对分析联系数在黑启动vague集决策中的应用研究 ·633. 联性的问题,但计算复杂,由于vague集是一个含有 (1)类似的归一化处理,则得 不确定性的集合,借用vag如e集可以方便地描述一 u=a bi+cj 个模糊的不确定信息,却为建模计算带来麻烦:而忽 联系数的运算 略vague集的不确定性,虽可以使计算得以具体操 作,但同时也丢失了vague集含带的不确定性信息, 为了便于叙述,这里只介绍本文所用联系数 严重时可能使决策结果偏离实际。 u=a+bi的普通加法与乘法运算[&9,20]。 鉴于此,本文把集对分析联系数用于黑启动 2.1加法运算 vague集决策研究,理由是集对分析联系数作为处理 定义2设有联系数u1=a1+b,i,2=a2+ 系统不确定性信息的数学理论,得到广泛应用s1), b2i,则有 在供配电领域也有不少应用,如文献[11]建立了基 u=u1+2=(a1+a2)+(b1+b2)i=a+bi 于联系数模型的电网灵活规划方法,文献[12]把联 定义2给出的联系数加法运算可以推广到3个或3 系数用于配电系统可靠性评估,文献[13]把联系数 个以上联系数相加,并满足交换律和结合律(证明 用于计及可靠性参数影响的电压暂降频次评估,文 略)。 献[14]把集对分析联系数用于输变电工程风险评 2.2乘法运算 估,文献[15-16]则把集对分析用于电能质量评估。 定义3设有联系数u=a+bi是n个联系数的 此外,文献[17]把集对分析联系数用于直觉模糊多 和,则有 属性决策的改进,而文献[18]在1996年就指出 111, vague集其实就是直觉模糊集。受上述文献启发,本 nu=natmbi=u n n 文把集对分析联系数用于vague数据环境下黑启动 即为μ的平均联系数。 多方案选优排序的分析计算,给出一种既简明又便 定义4设有联系数u1=a1+bi、2=a2+ 于作不确定性分析的黑启动vague集决策新方法。 b2i,则它们的乘积 1集对分析与联系数简介 u=u2=(a1+bi)(a2+b2i)= aja2 (ab2 azb)i+b bi2 (2) 1.1集对分析 由于i∈[-1,1],则”∈[-1,1](n=1,2,…)。 具有一定联系的两个集合组成的系统称集对。 如,某电力系统故障需分2个阶段修复,第1阶段计 用E、F表示集合,H表示集对,则H=(E,F)。 划8h完成,若顺利可提早2h,有意外需增加2h, 集对是一种客观现象,如正电与负电,系统的输 即需时间8+2i;如第2阶段需时5+1i,则共需 入与输出等,都可以在一定条件下看成是一个集对。 13+3i(引起所需时间变化的原因可能不同,但结 在一定的问题背景下,分析集对中两个集合的所有关 果相同,即最少10h,最多16h):如每小时需费用为 系,并把这些关系分成相对确定与相对不确定的关系 1000+150i,则所需全部费用为(13+3i)(1000+ 两类(或分成同异反关系三类或更多),用联系数描述 150i)=13000+1950i+3000i+4502=13000+ 这些关系的多少,该联系数称为集对的特征函数:再 5400i(引起工期变化和所需费用变化的原因可能 建立适当联系数模型,借助模型作进一步的分析。 完全不同,但所需费用范围的分析结果却相同),最 1.2联系数 节约即取i=-1时,需7600元:最大费用即取i=1 集对分析联系数有不同的数学表达式[81]。下 时,需18400元,等等。因此,在不需要计及不确定 面仅列出二元联系数和三元联系数的定义。 性层次性时,为简化分析计算,可以有 定义1设集对H=(E,F)在问题W中的全部 i=i2=i=…=0no0 关系数为N,A、B分别为相对确定和相对不确定的 这一简化公式,据此,可以把式(2)改写成: 关系数,则称u=A+Bi为二元联系数;i为不确定 u=u2=aaz+(ab2 +ab +bb2)i=a bi 系数,在【-1,1]区间视不同情况取值。若令N= 说明两个联系数相乘,其积仍是一个联系数。 A+B,u=/N,a=A/N,b=B/N,即得 3 vague集向联系数的转换 u=a bi (1) 为归一化处理后的二元联系数,a、b为联系数u的 3.1 vague的概念 联系分量。同理,u=A+Bi+G为三元联系数,也 定义5设x是给定论域U上的元素。U上的 称同异反联系数,C表示反关系,j=-1。若采用式 vague集V是指相关的一对隶属函数tv(x)和
联性的问题,但计算复杂,由于 vague 集是一个含有 不确定性的集合,借用 vague 集可以方便地描述一 个模糊的不确定信息,却为建模计算带来麻烦;而忽 略 vague 集的不确定性,虽可以使计算得以具体操 作,但同时也丢失了 vague 集含带的不确定性信息, 严重时可能使决策结果偏离实际。 鉴于此,本文把集对分析联系数用于黑启动 vague 集决策研究,理由是集对分析联系数作为处理 系统不确定性信息的数学理论,得到广泛应用[8⁃10] , 在供配电领域也有不少应用,如文献[11]建立了基 于联系数模型的电网灵活规划方法,文献[12]把联 系数用于配电系统可靠性评估,文献[13]把联系数 用于计及可靠性参数影响的电压暂降频次评估,文 献[14]把集对分析联系数用于输变电工程风险评 估,文献[15⁃16]则把集对分析用于电能质量评估。 此外,文献[17]把集对分析联系数用于直觉模糊多 属性决策的改进,而文献[ 18] 在 1996 年就指出 vague 集其实就是直觉模糊集。 受上述文献启发,本 文把集对分析联系数用于 vague 数据环境下黑启动 多方案选优排序的分析计算,给出一种既简明又便 于作不确定性分析的黑启动 vague 集决策新方法。 1 集对分析与联系数简介 1.1 集对分析 具有一定联系的两个集合组成的系统称集对。 用 E、F 表示集合,H 表示集对,则 H = (E,F) 。 集对是一种客观现象,如正电与负电,系统的输 入与输出等,都可以在一定条件下看成是一个集对。 在一定的问题背景下,分析集对中两个集合的所有关 系,并把这些关系分成相对确定与相对不确定的关系 两类(或分成同异反关系三类或更多),用联系数描述 这些关系的多少,该联系数称为集对的特征函数;再 建立适当联系数模型,借助模型作进一步的分析[19] 。 1.2 联系数 集对分析联系数有不同的数学表达式[8⁃12] 。 下 面仅列出二元联系数和三元联系数的定义。 定义 1 设集对 H = (E,F) 在问题 W 中的全部 关系数为 N,A、B 分别为相对确定和相对不确定的 关系数,则称 u = A + Bi 为二元联系数; i 为不确定 系数,在 [ - 1,1] 区间视不同情况取值。 若令 N = A + B , μ = u / N , a = A / N , b = B / N ,即得 μ = a + bi (1) 为归一化处理后的二元联系数, a 、 b 为联系数 μ 的 联系分量。 同理, u = A + Bi + Cj 为三元联系数,也 称同异反联系数,C 表示反关系, j = - 1。 若采用式 (1)类似的归一化处理,则得 μ = a + bi + cj 2 联系数的运算 为了便于叙述,这里只介绍本文所用联系数 μ =a + bi 的普通加法与乘法运算[8⁃9,20] 。 2.1 加法运算 定义 2 设有联系数 μ1 = a1 + b1 i , μ2 = a2 + b2 i, 则有 μ = μ1 + μ2 = (a1 + a2 ) + (b1 + b2 )i = a + bi 定义 2 给出的联系数加法运算可以推广到 3 个或 3 个以上联系数相加,并满足交换律和结合律(证明 略)。 2.2 乘法运算 定义 3 设有联系数 μ = a + bi 是 n 个联系数的 和,则有 1 n μ = 1 n a + 1 n bi = μ - 即为 μ 的平均联系数。 定义 4 设有联系数 μ1 = a1 + b1 i 、 μ2 = a2 + b2 i, 则它们的乘积 μ = μ1μ2 = (a1 + b1 i)(a2 + b2 i) = a1 a2 + (a1 b2 + a2 b1 )i + b1 b2 i 2 (2) 由于 i ∈ [ - 1,1] ,则 i n ∈ [ - 1,1] (n = 1,2,…) 。 如,某电力系统故障需分 2 个阶段修复,第 1 阶段计 划 8 h 完成,若顺利可提早 2 h,有意外需增加 2 h, 即需时间 8 + 2i ;如第 2 阶段需时 5 + 1i ,则共需 13 +3i (引起所需时间变化的原因可能不同,但结 果相同,即最少 10h,最多 16 h);如每小时需费用为 1 000 +150i ,则所需全部费用为 (13 + 3i)(1 000 + 150i) = 13 000 + 1 950i + 3 000i + 450i 2 = 13 000 + 5 400i (引起工期变化和所需费用变化的原因可能 完全不同,但所需费用范围的分析结果却相同),最 节约即取 i = - 1 时,需 7 600 元;最大费用即取 i = 1 时,需 18 400 元,等等。 因此,在不需要计及不确定 性层次性时,为简化分析计算,可以有 i = i 2 = i 3 = … = i n n → ¥ 这一简化公式,据此,可以把式(2)改写成: μ = μ1μ2 = a1 a2 + (a1 b2 + a2 b1 + b1 b2 )i = a + bi 说明两个联系数相乘,其积仍是一个联系数。 3 vague 集向联系数的转换 3.1 vague 的概念 定义 5 设 x 是给定论域 U 上的元素。 U 上的 vague 集 V 是 指 相 关 的 一 对 隶 属 函 数 tV(x) 和 第 5 期 赵玉铃,等:集对分析联系数在黑启动 vague 集决策中的应用研究 ·633·

·634· 智能系统学报 第9卷 f(x),t(x):U→[0,1]和f(x):U→[0,1]满足 启动路径上变电站的个数、启动时间、被启动机组的 0≤t,(x)+f(x)≤1,tv(x)为vague集V的真隶属 容量等为定量指标,启动路径上负荷的重要性等级、 函数,表示支持x∈V的证据的隶属度下界;f(x) 机组状态等为定性指标,计算时,需要把定性指标化 为vague集V的假隶属函数,表示反对x∈V的证据 为定量指标。又由于指标的量纲不一,所以,还需作 的隶属度下界,如图1所示。下文将vague集V简 规范化处理,处理时要注意指标的属性。当然,这些 记为(x,t(x),f(x))或(t(x)f(x)。 指标数据最后都用vague集表示,设第k个指标c的 1.0 指标数据用p(c)表示。 -f(x) 4.1.2指标权重W(c) 食 0.5 指标权重反映该指标的重要程度,通常用介于 0~1之间的点实数表示,但这里也用vague集表示。 (x) 另外,黑启动方案评价中涉及到的指标一般情 况下并不是相互独立的。如黑启动路径上变电站个 图1 Vague集 数的增大会延长黑启动时间,待启动机组的额定容 Fig.1 Vague set 量与启动电能相关等。为此,用W(c,c+1)表示2 以上是文献[7]对vague集的定义。 个指标的关联权重,用W(c,c+1,c+2)表示3个指 3.2 vague集的不确定度 标的关联权重,依此类推。当然,所有的权重数据也 由于vague集V中0≤t,(x)+f,(x)≤l,可令 都用vague集表示。 T(x)=1-t(x)-f(x) (3) 4.1.3专家人数与专家权重 称Tv(x)为vague集V的不确定度。 黑启动方案选优与决策过程通常需要有多个专 3.3 vague集的不确定性及其特征联系数 家参与,但专家在决策过程中所起的作用有大小之 从定义5可见,vague集V中的t(x)与f(x) 分。因此,需要根据发挥的作用大小给参与黑启动 是相对确定的,可以组成相对确定的集合E= 的专家分配一定的权重,用W(E)表示第j位专家 (t,(x),f(x));π(x)是相对不确定的一个元素, 的权重。但正如文献[7]所指,专家对指标及指标 组成集合F=T,(x)。于是,一个vague集V可以表 数据的偏好受到其知识、经验、权力及社会地位等因 示成一个集对V=(E,F)或 素的影响,相互之间也存在一定的关联性。2个专 V=(t(x)+f(x)),T(x)) 家之间的关联权重用W(E,E1)表示,3个专家之 既然vague集V可以组成一个集对,则这个集对的 间的关联权重用W(E,E1,E+2)表示,依此类推。 特征函数可以用4=a+bi+cg或μ=a+bi的形式 这些专家权重也用vague集表示。 来表示。令t,(x)=a,f(x)=c,T(x)=b,则 4.2群决策模型 vague集V就可以写成 4.2.1基本模型 当黑启动方案评价指标数据p(c:)(k=1,2, vaguev=a bi cj (4) …,n)都是越大越好型数据,越重要的指标权重 结合式(3)得a+b+c=1,故用a+bi描述vague集 W(c)也越大,越重要的专家权重W(E)(j=1,2, V时也完全考虑了“反”f(x)=c的变化情况,因此, …,p)也越大时,黑启动评价基本模型为 也可以把a+bi作为vague集V的特征函数,即 vagueV=a+bii∈[-1,l] (5) M(S)= 立.(G)e) (8) k= 选用式(4)还是式(5)作为vague集V的特征联系 其中 数,由实际问题定。在本文研究中,拟用式(5),称 式(5)是一个vague集向联系数的转换公式,其中: W(c4)=∑W(ca)EW(E,) (9) i=1 a=ty(x) (6) Sn代表第v个方案(v=1,2,…,m),M(Sn)表示第 b=T(x) (7) :个方案的综合评价值,P.(c)表示第,个方案的指 4联系数表示的黑启动决策模型 标k(k=1,2,…,n)的值,W(c)表示指标ck的权 重,W(E)表示专家权重。 4.1黑启动群决策的vague数据 m个方案的优劣评价准则为:M(S,)值大的优 4.1.1黑启动方案的评价指标数据 于M(S)值小的。 这类指标通常有定量指标和定性指标两类,黑 4.2.2关联模型
fV(x),tV(x) :U→[0,1] 和 fV(x) :U→[0,1] 满足 0 ≤tV(x) + fV(x) ≤1, tV(x) 为 vague 集 V 的真隶属 函数,表示支持 x ∈ V 的证据的隶属度下界; fV(x) 为 vague 集 V 的假隶属函数,表示反对 x ∈ V 的证据 的隶属度下界,如图 1 所示。 下文将 vague 集 V 简 记为 (x,tV(x),fV(x)) 或 (tV(x),fV(x)) 。 图 1 Vague 集 Fig.1 Vague set 以上是文献[7]对 vague 集的定义。 3.2 vague 集的不确定度 由于 vague 集 V 中 0 ≤ tV(x) + fV(x) ≤ 1,可令 πV(x) = 1 - tV(x) - fV(x) (3) 称 πV(x) 为 vague 集 V 的不确定度。 3.3 vague 集的不确定性及其特征联系数 从定义 5 可见,vague 集 V 中的 tV(x) 与 fV(x) 是相 对 确 定 的, 可 以 组 成 相 对 确 定 的 集 合 E = (tV(x),fV(x)) ; πV(x) 是相对不确定的一个元素, 组成集合 F = πV(x) 。 于是,一个 vague 集 V 可以表 示成一个集对 V = (E,F) 或 V = ((tV(x) + fV(x)),πV(x)) 既然 vague 集 V 可以组成一个集对,则这个集对的 特征函数可以用 μ = a + bi + cj 或 μ = a + bi 的形式 来表示。 令 tV(x) = a , fV(x) = c , πV(x) = b ,则 vague 集 V 就可以写成 vagueV = a + bi + cj (4) 结合式(3)得 a + b + c = 1,故用 a + bi 描述 vague 集 V 时也完全考虑了“反” fV(x) = c 的变化情况,因此, 也可以把 a + bi 作为 vague 集 V 的特征函数,即 vagueV = a + bi i ∈ [ - 1,1] (5) 选用式(4)还是式(5)作为 vague 集 V 的特征联系 数,由实际问题定。 在本文研究中,拟用式(5),称 式(5)是一个 vague 集向联系数的转换公式,其中: a = tV(x) (6) b = πV(x) (7) 4 联系数表示的黑启动决策模型 4.1 黑启动群决策的 vague 数据 4.1.1 黑启动方案的评价指标数据 这类指标通常有定量指标和定性指标两类,黑 启动路径上变电站的个数、启动时间、被启动机组的 容量等为定量指标,启动路径上负荷的重要性等级、 机组状态等为定性指标,计算时,需要把定性指标化 为定量指标。 又由于指标的量纲不一,所以,还需作 规范化处理,处理时要注意指标的属性。 当然,这些 指标数据最后都用 vague 集表示,设第 k 个指标 c 的 指标数据用 p(ck) 表示。 4.1.2 指标权重 W(ck) 指标权重反映该指标的重要程度,通常用介于 0~1 之间的点实数表示,但这里也用 vague 集表示。 另外,黑启动方案评价中涉及到的指标一般情 况下并不是相互独立的。 如黑启动路径上变电站个 数的增大会延长黑启动时间,待启动机组的额定容 量与启动电能相关等。 为此,用 W(ck,ck+1 ) 表示 2 个指标的关联权重,用 W(ck,ck+1 ,ck+2 ) 表示 3 个指 标的关联权重,依此类推。 当然,所有的权重数据也 都用 vague 集表示。 4.1.3 专家人数与专家权重 黑启动方案选优与决策过程通常需要有多个专 家参与,但专家在决策过程中所起的作用有大小之 分。 因此,需要根据发挥的作用大小给参与黑启动 的专家分配一定的权重,用 W(Ej) 表示 第 j 位 专家 的权重。 但正如文献[7]所指,专家对指标及指标 数据的偏好受到其知识、经验、权力及社会地位等因 素的影响,相互之间也存在一定的关联性。 2 个专 家之间的关联权重用 W(Ej,Ej+1 ) 表示,3 个专家之 间的关联权重用 W(Ej,Ej+1 ,Ej+2 ) 表示,依此类推。 这些专家权重也用 vague 集表示。 4.2 群决策模型 4.2.1 基本模型 当黑启动方案评价指标数据 p(ck) ( k = 1,2, …,n ) 都是越大越好型数据,越重要的指标权重 W(ck) 也越大,越重要的专家权重 W(Ej) ( j = 1,2, …,p )也越大时,黑启动评价基本模型为 M(Sv) = ∑ n k = 1 pv(ck)W(ck) (8) 其中 W(ck) = ∑ p j = 1 W (ck) Ej W(Ej) (9) Sv 代表第 v 个方案( v = 1,2,…,m ), M(Sv) 表示第 v 个方案的综合评价值, pv(ck) 表示第 v 个方案的指 标 k(k = 1,2,…,n) 的值, W(ck) 表示指标 ck 的权 重, W(Ej) 表示专家权重。 m 个方案的优劣评价准则为: M(Sv) 值大的优 于 M(Sv) 值小的。 4.2.2 关联模型 ·634· 智 能 系 统 学 报 第 9 卷

第5期 赵玉铃,等:集对分析联系数在黑启动vgue集决策中的应用研究 ·635. 当计及指标与指标之间的关联性、专家与专家 关于指标的关联权重“平均分摊”给相关联的各个 之间的关联性时,式(8)、(9)变为 指标,第2次平均是指2”/2个被平均分摊后的关联 权重加和后再平均(算术平均)。 M(S)=】 p.(c)W(c4,4…) -1 3)根据上述分析得出每个专家共2/2个平均 W(c)=】 W(e,g…)gw(E,Er1…) 关联权重的平均值: 于是,关键的问题就转化为如何从p个专家给出的 W(E)= 2 关于指标c:的关联权重,计算出该指标的权重,以 Wc(E1,E2,…,Eo),G=1,2,…,2 满足式(8)的计算。 4)用类似于前3步的方法计算各指标的(独 4.3专家关联权重与指标关联权重的计算 立)权重。 设有p(p>0)个相互有关联的专家对n个相 4.4不确定性分析 互有关联的指标赋权,且专家的关联权重和指标的 把给出的各指标值vague集,参照式(5)~(7) 关联权重都用vague集表示。 改写成a+bi形式的联系数,并利用式(8)算得各方 1)利用式(5)~(7)把各vague集转化为a+bi 案的综合评价联系数;再令联系数中的i=-1、 形式的联系数。 -0.5、0、0.5、1等典型值,得到各方案的评价值在不 2)把Q个专家之间的关联权重W(E,E2,…, 同情况下的变动趋势:根据变动趋势,决出最优方 E。)一一折算给各个关联专家,即得平均关联权重 案,并给出被评价诸方案的优劣排序。 很明显,不确定系数i是联系数的关键所在,它 W(E,E2,…,Eo)的计算公式: 形式上是一个数,但同时又是不确定性系统的一个 W(E,B,…,Eo)=Or(E1,E,E) 代号,需要结合问题的实际作系统分析:但是当问题 因为根据集合论知识,一个有p个专家组成的集合, 本身没有提供不确定性系统的具体信息时,只能根 其子集个数为2”个,关联性的子集有2”/2个。为了 据i的定义域作纯数学意义上的取值分析,借此检 计算方便并便于比较待评方案的优劣,必须把这 验黑启动决策结论的可靠性和客观合理性。 2”/2个关联权重折算为某个指标在非关联意义下 5实例 的权重(本文称为独立权重)。由于缺乏关联程度 的具体信息(当专家E,对专家E,的关联权值是R 为便于比较,此处引用文献[7]中的例子说明 时,E,对E,的关联权值不一定是R),只能作平均 前述方法的应用。某地区电力系统事故后需要黑启 分配,即假定所谓关联是相互之间的一种作用,这种 动,共有6个待评价的方案,方案的评价指标数为4 相互作用大小相等,作用在相互关联的专家之间,所 个,各方案在各指标上的vague集数据已经规范化 以作“平均分配”。第1次平均是把给出的每一个 处理成越大越好型数据,见表1。 表1各个候选黑启动方案的指标值 Table 1 The index value of each candidate in black-start 方案 机组状态c, 爬坡速率c2 机组容量c 变电站个数c4 1 (0.30.0.50) (0.96.0.04) (1.00.0.00) (0.20.0.80) 2 (0.60.0.17) (0.53.0.47) (0.67,0.33) (0.25.0.75) 3 (0.45.0.33) (1.00,0.00) (0.42.0.58 (0.33,0.67) 4 (0.30.0.50) (0.50,0.50) (0.42,0.58) (0.33,0.67) 5 (0.60.0.17) (0.27,0.73) (0.42.0.58 (1.00.0.00) 6 (0.90,0.00) (0.91,0.09) (0.67,0.33) (0.25,0.75) 参与黑启动决策专家共3人E=(e1,e2,e3),权 W({e2,e3})=(0.70,0.20) 重、关联权重分别为 w({e1,e2,e3})=(1.00,0.00) w({e1})=(0.30,0.60) 专家e,给出的各指标权重、关联权重如下: W({e2})=(0.40,0.50) W({c1})=(0.10,0.65) W({e3})=(0.40,0.30) W({c2})=(0.25,0.55) W({e1,e2})=(0.60,0.20) W({c3})=(0.20,0.50) W({e1,e3})=(0.70,0.10) W({ca})=(0.20,0.70)
当计及指标与指标之间的关联性、专家与专家 之间的关联性时,式(8)、(9)变为 M(Sv) = ∑ n k = 1 pv(ck)W(ck,ck+q,…) W(ck) = ∑ p j = 1 W (ck,ck+q,…) Ej W(Ej,Ej+1 ,…) 于是,关键的问题就转化为如何从 p 个专家给出的 关于指标 ck 的关联权重,计算出该指标的权重,以 满足式(8)的计算。 4.3 专家关联权重与指标关联权重的计算 设有 p(p > 0) 个相互有关联的专家对 n 个相 互有关联的指标赋权,且专家的关联权重和指标的 关联权重都用 vague 集表示。 1) 利用式(5) ~ (7)把各 vague 集转化为 a + bi 形式的联系数。 2) 把 Q 个专家之间的关联权重 W(E1 ,E2 ,…, EQ) 一一折算给各个关联专家,即得平均关联权重 W - (E1 ,E2 ,…,EQ) 的计算公式: W - (E1 ,E2 ,…,EQ) = 1 Q W(E1 ,E2 ,…,EQ) 因为根据集合论知识,一个有 p 个专家组成的集合, 其子集个数为 2 p 个,关联性的子集有 2 p / 2 个。 为了 计算方便并便于比较待评方案的优劣,必须把这 2 p / 2 个关联权重折算为某个指标在非关联意义下 的权重(本文称为独立权重)。 由于缺乏关联程度 的具体信息(当专家 E1 对专家 E2 的关联权值是 R 时, E2 对 E1 的关联权值不一定是 R),只能作平均 分配,即假定所谓关联是相互之间的一种作用,这种 相互作用大小相等,作用在相互关联的专家之间,所 以作“平均分配”。 第 1 次平均是把给出的每一个 关于指标的关联权重“平均分摊”给相关联的各个 指标,第 2 次平均是指 2 p / 2 个被平均分摊后的关联 权重加和后再平均(算术平均)。 3) 根据上述分析得出每个专家共 2 p / 2 个平均 关联权重的平均值: W(Ej) = 2 2 p∑ 2 p 2 G = 1 WG (E1 ,E2 ,…,EQ),G = 1,2,…, 2 p 2 4) 用类似于前 3 步的方法计算各指标的(独 立)权重。 4.4 不确定性分析 把给出的各指标值 vague 集,参照式(5) ~ (7) 改写成 a + bi 形式的联系数,并利用式(8)算得各方 案的综合评价联系数;再令联系数中的 i = - 1、 -0.5、0、0.5、1 等典型值,得到各方案的评价值在不 同情况下的变动趋势;根据变动趋势,决出最优方 案,并给出被评价诸方案的优劣排序。 很明显,不确定系数 i 是联系数的关键所在,它 形式上是一个数,但同时又是不确定性系统的一个 代号,需要结合问题的实际作系统分析;但是当问题 本身没有提供不确定性系统的具体信息时,只能根 据 i 的定义域作纯数学意义上的取值分析,借此检 验黑启动决策结论的可靠性和客观合理性。 5 实例 为便于比较,此处引用文献[7]中的例子说明 前述方法的应用。 某地区电力系统事故后需要黑启 动,共有 6 个待评价的方案,方案的评价指标数为 4 个,各方案在各指标上的 vague 集数据已经规范化 处理成越大越好型数据,见表 1。 表 1 各个候选黑启动方案的指标值 Table 1 The index value of each candidate in black⁃start 方案 机组状态 c1 爬坡速率 c2 机组容量 c3 变电站个数 c4 1 2 3 4 5 6 (0.30,0.50) (0.60,0.17) (0.45,0.33) (0.30,0.50) (0.60,0.17) (0.90,0.00) (0.96,0.04) (0.53,0.47) (1.00,0.00) (0.50,0.50) (0.27,0.73) (0.91,0.09) (1.00,0.00) (0.67,0.33) (0.42,0.58) (0.42,0.58) (0.42,0.58) (0.67,0.33) (0.20,0.80) (0.25,0.75) (0.33,0.67) (0.33,0.67) (1.00,0.00) (0.25,0.75) 参与黑启动决策专家共 3 人 Ej = (e1 ,e2 ,e3 ), 权 重、关联权重分别为 W( e1 { } ) = (0.30,0.60) W( e2 { } ) = (0.40,0.50) W( e3 { } ) = (0.40,0.30) W( e1 ,e2 { } ) = (0.60,0.20) W( e1 ,e3 { } ) = (0.70,0.10) W( e2 ,e3 { } ) = (0.70,0.20) W( e1 ,e2 ,e3 { } ) = (1.00,0.00) 专家 e1 给出的各指标权重、关联权重如下: W( c1 { } ) = (0.10,0.65) W( c2 { } ) = (0.25,0.55) W( c3 { } ) = (0.20,0.50) W( c4 { } ) = (0.20,0.70) 第 5 期 赵玉铃,等:集对分析联系数在黑启动 vague 集决策中的应用研究 ·635·

·636 智能系统学报 第9卷 W({c1,c2})=(0.30,0.40) 表2黑启动专家的权重W(©)计算 W({c2,c3})=(0.50,0.25) Table 2 The weight calculation of black-start expert W({c2,c})=(0.45,0.35) W(e,) W(e2) W(e3) W({c3,c4})=(0.40,0.30) 0.3+0.1i 0.4+0.1i 0.4+0.3i W({c1,c3})=(0.30,0.30) 1 W({c1,c})=(0.30,0.40) (0.6+0.2) 2a6+02007+020 W({c2,c3,c4})=(0.85,0.10) W({c1,c3,c4))=(0.70,0.20) 07+02)2a7+01n 1 (07+0.1i) 1 W({c1,c2,ca})=(0.65,0.30) 号1+0) 号1+0) 3(1+0) W({c1,c2,c3})=(0.75,0.20) 0.32075+ 0.34575+ 0.35825+ W({c1,c2,c3,c4})=(1.00,0.00) 平均 0.075i 0.0625i 0.1125i 专家e2、©给出的各指标权重、关联权重数据见 附录。计算和决策过程如下: 2)根据式(5)~(7)计算专家e1给出的黑启动 1)根据式(5)~(7)计算3位专家权重如表2。 指标权重及计及专家权重后的各指标权重,见表3。 表3专家©,给出的黑启动指标关联权重联系数 Table 3 The black-start index weight coefficient connection number given by expert e 专家 指标c 指标c2 指标c3 指标c4 0.1+0.25i 0.25+0.20i 0.2+0.3i 0.2+0.1i 2(03+0.3 1 ÷a3+a3刘 2(0.5+0.25i) (045+0.2) 1 (03+Q.4) 1 (0.5+0.25) (0.4+0.30) 1 2(0.4+Q.3) (0.3+Q3) 1 2(045+0.2) 1 (03+0.4) 1 a3+0 7(0.70+0.10) (0.85+0.05) 085+0.0s) 3(0.85+0.05) 3(0.65+Q.050) ,(0.65+0.05i) 号Q0+a1a 5(0.70+0.10i) 3(0.75+Q.05) 3(0.75+Q05) 3(0.75+0.05) 3(0.65+Q05) (1+0) 1 4(1+0) (1+0) 1 1+a) (0.1875+0.1021i)× (0.2344+0.0783i)× (0.227+0.1053i)× (0.2291+0.0709i)× 平均权重 (0.32075+0.075i)= (0.32075+0.075i)= (0.32075+0.075i)= 联系数 (0.32075+0.075i)= 0.0601+0.0546i 0.0752+0.0486i 0.0728+0.0587i 0.0735+0.0452i 专家e2、e3给出的黑启动指标权重以及计及专 表4用联系数表示的各个候选黑启动方案指标值 家权重后的各指标权重见附录。 Table 4 Every candidate black-start scheme index value expressed by connection number 由此得出,把各专家权重计入各指标的权重后 方案 C3 相加得到各指标的权重联系数如下: c2 10.30+0.20i0.96+0i 1+0i 0.2+0i W(c)=0.2034+0.1877i 20.60+0.23i 0.53+0i0.67+0i0.25+0i W(c2)=0.2116+0.1732i 30.45+0.22i 1+0i0.42+0i0.33+0i 40.30+0.20i 0.50+0i0.42+0i0.33+0i W(c3)=0.2144+0.1797i 50.60+0.23i0.27+0i0.42+0i1+0i W(c4)=0.2255+0.1702i 60.90+0.10i0.91+0i0.67+0i0.25+0i 3)把表1中的各vague集数据改写成联系数, 4)利用表4,并结合第2步得到的各指标权重, 得表4。 采用式(8)算得各方案的综合评价值联系数为
W( c1 ,c2 { } ) = (0.30,0.40) W( c2 ,c3 { } ) = (0.50,0.25) W( c2 ,c4 { } ) = (0.45,0.35) W( c3 ,c4 { } ) = (0.40,0.30) W( c1 ,c3 { } ) = (0.30,0.30) W( c1 ,c4 { } ) = (0.30,0.40) W( c2 ,c3 ,c4 { } ) = (0.85,0.10) W( c1 ,c3 ,c4 { } ) = (0.70,0.20) W( c1 ,c2 ,c4 { } ) = (0.65,0.30) W( c1 ,c2 ,c3 { } ) = (0.75,0.20) W( c1 ,c2 ,c3 ,c4 { } ) = (1.00,0.00) 专家 e2 、 e3 给出的各指标权重、关联权重数据见 附录。 计算和决策过程如下: 1) 根据式(5) ~ (7)计算 3 位专家权重如表 2。 表 2 黑启动专家的权重 W(ej) 计算 Table 2 The weight calculation of black⁃start expert W(e1 ) W(e2 ) W(e3 ) 0.3 + 0.1i 1 2 (0.6 + 0.2i) 1 2 (0.7 + 0.2i) 1 3 (1 + 0i) 0.4 + 0.1i 1 2 (0.6 + 0.2i) 1 2 (0.7 + 0.1i) 1 3 (1 + 0i) 0.4 + 0.3i 1 2 (0.7 + 0.2i) 1 2 (0.7 + 0.1i) 1 3 (1 + 0i) 平均 0.32075 + 0.075i 0.34575 + 0.0625i 0.35825 + 0.1125i 2) 根据式(5) ~ (7)计算专家 e1 给出的黑启动 指标权重及计及专家权重后的各指标权重,见表 3。 表 3 专家 e1 给出的黑启动指标关联权重联系数 Table 3 The black⁃start index weight coefficient connection number given by expert e1 专家 指标 c1 指标 c2 指标 c3 指标 c4 e1 0.1 + 0.25i 1 2 (0.3 + 0.3i) 1 2 (0.3 + 0.4i) 1 2 (0.3 + 0.3i) 1 3 (0.70 + 0.10i) 1 3 (0.65 + 0.05i) 1 3 (0.75 + 0.05i) 1 4 (1 + 0i) 0.25 + 0.20i 1 2 (0.3 + 0.3i) 1 2 (0.5 + 0.25i) 1 2 (0.45 + 0.2i) 1 3 (0.85 + 0.05i) 1 3 (0.65 + 0.05i) 1 3 (0.75 + 0.05i) 1 4 (1 + 0i) 0.2 + 0.3i 1 2 (0.5 + 0.25i) 1 2 (0.4 + 0.3i) 1 2 (0.3 + 0.4i) 1 3 (0.85 + 0.05i) 1 3 (0.70 + 0.10i) 1 3 (0.75 + 0.05i) 1 4 (1 + 0i) 0.2 + 0.1i 1 2 (0.45 + 0.2i) 1 2 (0.4 + 0.3i) 1 2 (0.3 + 0.3i) 1 3 (0.85 + 0.05i) 1 3 (0.70 + 0.10i) 1 3 (0.65 + 0.05i) 1 4 (1 + 0i) 平均权重 联系数 (0.1875+0.1021i)× (0.32075+0.075i)= 0.0601+0.0546i (0.2344+0.0783i)× (0.32075+0.075i)= 0.0752+0.0486i (0.227+0.1053i)× (0.32075+0.075i)= 0.0728+0.0587i (0.2291+0.0709i)× (0.32075+0.075i)= 0.0735+0.0452i 专家 e2 、 e3 给出的黑启动指标权重以及计及专 家权重后的各指标权重见附录。 由此得出,把各专家权重计入各指标的权重后 相加得到各指标的权重联系数如下: W(c1 ) = 0.2034 + 0.1877i W(c2 ) = 0.2116 + 0.1732i W(c3 ) = 0.2144 + 0.1797i W(c4 ) = 0.2255 + 0.1702i 3) 把表 1 中的各 vague 集数据改写成联系数, 得表 4。 表 4 用联系数表示的各个候选黑启动方案指标值 Table 4 Every candidate black⁃start scheme index value expressed by connection number 方案 c1 c2 c3 c4 1 2 3 4 5 6 0.30 + 0.20i 0.60 + 0.23i 0.45 + 0.22i 0.30 + 0.20i 0.60 + 0.23i 0.90 + 0.10i 0.96 + 0i 0.53 + 0i 1 + 0i 0.50 + 0i 0.27 + 0i 0.91 + 0i 1 + 0i 0.67 + 0i 0.42 + 0i 0.42 + 0i 0.42 + 0i 0.67 + 0i 0.2 + 0i 0.25 + 0i 0.33 + 0i 0.33 + 0i 1 + 0i 0.25 + 0i 4) 利用表 4,并结合第 2 步得到的各指标权重, 采用式(8)算得各方案的综合评价值联系数为 ·636· 智 能 系 统 学 报 第 9 卷
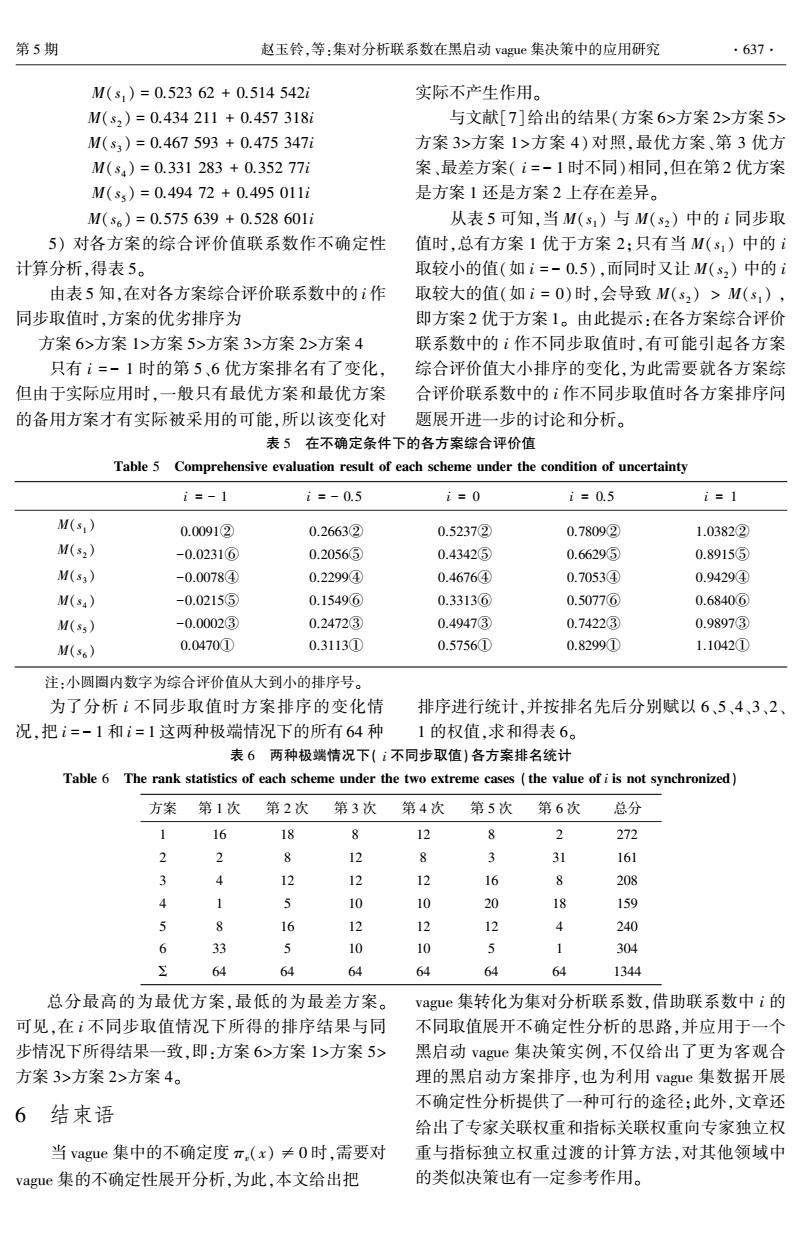
第5期 赵玉铃,等:集对分析联系数在黑启动vgue集决策中的应用研究 ·637. M(s1)=0.52362+0.514542i 实际不产生作用。 M(s2)=0.434211+0.457318i 与文献[7]给出的结果(方案6>方案2>方案5> M(s3)=0.467593+0.475347i 方案3>方案1>方案4)对照,最优方案、第3优方 M(s4)=0.331283+0.35277i 案、最差方案(i=-1时不同)相同,但在第2优方案 M(s5)=0.49472+0.495011i 是方案1还是方案2上存在差异。 M(s6)=0.575639+0.528601i 从表5可知,当M(s1)与M(s2)中的i同步取 5)对各方案的综合评价值联系数作不确定性 值时,总有方案1优于方案2;只有当M(s1)中的i 计算分析,得表5。 取较小的值(如i=-0.5),而同时又让M(s2)中的i 由表5知,在对各方案综合评价联系数中的i作 取较大的值(如i=0)时,会导致M(s2)>M(s1), 同步取值时,方案的优劣排序为 即方案2优于方案1。由此提示:在各方案综合评价 方案6>方案1>方案5>方案3>方案2>方案4 联系数中的i作不同步取值时,有可能引起各方案 只有i=-1时的第5、6优方案排名有了变化, 综合评价值大小排序的变化,为此需要就各方案综 但由于实际应用时,一般只有最优方案和最优方案 合评价联系数中的辶作不同步取值时各方案排序问 的备用方案才有实际被采用的可能,所以该变化对 题展开进一步的讨论和分析。 表5在不确定条件下的各方案综合评价值 Table 5 Comprehensive evaluation result of each scheme under the condition of uncertainty i=-1 i=-0.5 i=0 i=0.5 i=1 M(s1) 0.0091② 0.2663② 0.52372 0.78092 1.0382② M(s2) -0.02316 0.2056⑤ 0.4342⑤ 0.6629⑤ 0.8915⑤ M(s3) -0.00784④ 0.2299④ 0.4676④ 0.70534 0.9429④ M(s4) -0.0215⑤ 0.1549⑥ 0.3313⑥ 0.50776 0.68406 M(s5) -0.00023 0.2472③ 0.49473 0.74223 0.98973 M(s6) 0.0470① 0.3113① 0.5756① 0.8299① 1.1042① 注:小圆圈内数字为综合评价值从大到小的排序号。 为了分析i不同步取值时方案排序的变化情 排序进行统计,并按排名先后分别赋以6、5、4、3、2、 况.把i=-1和i=1这两种极端情况下的所有64种 1的权值,求和得表6。 表6两种极端情况下(i不同步取值)各方案排名统计 Table 6 The rank statistics of each scheme under the two extreme cases (the value of i is not synchronized) 方案第1次第2次第3次第4次第5次 第6次 总分 1 16 18 12 8 2 272 2 2 8 12 8 3 31 161 3 4 12 12 12 16 8 208 4 1 5 10 10 20 18 159 8 16 12 12 4 240 6 33 5 10 10 5 1 304 64 64 64 64 64 64 1344 总分最高的为最优方案,最低的为最差方案。 vague集转化为集对分析联系数,借助联系数中i的 可见,在i不同步取值情况下所得的排序结果与同 不同取值展开不确定性分析的思路,并应用于一个 步情况下所得结果一致,即:方案6>方案1>方案5> 黑启动vague集决策实例,不仅给出了更为客观合 方案3>方案2>方案4。 理的黑启动方案排序,也为利用vague集数据开展 6结束语 不确定性分析提供了一种可行的途径:此外,文章还 给出了专家关联权重和指标关联权重向专家独立权 当vague集中的不确定度π(x)≠0时,需要对 重与指标独立权重过渡的计算方法,对其他领域中 vague集的不确定性展开分析,为此,本文给出把 的类似决策也有一定参考作用
M(s1 ) = 0.523 62 + 0.514 542i M(s2 ) = 0.434 211 + 0.457 318i M(s3 ) = 0.467 593 + 0.475 347i M(s4 ) = 0.331 283 + 0.352 77i M(s5 ) = 0.494 72 + 0.495 011i M(s6 ) = 0.575 639 + 0.528 601i 5) 对各方案的综合评价值联系数作不确定性 计算分析,得表 5。 由表 5 知,在对各方案综合评价联系数中的 i 作 同步取值时,方案的优劣排序为 方案 6>方案 1>方案 5>方案 3>方案 2>方案 4 只有 i = - 1 时的第 5、6 优方案排名有了变化, 但由于实际应用时,一般只有最优方案和最优方案 的备用方案才有实际被采用的可能,所以该变化对 实际不产生作用。 与文献[7]给出的结果(方案 6>方案 2>方案 5> 方案 3>方案 1>方案 4) 对照,最优方案、第 3 优方 案、最差方案( i = - 1 时不同)相同,但在第 2 优方案 是方案 1 还是方案 2 上存在差异。 从表 5 可知,当 M(s1 ) 与 M(s2 ) 中的 i 同步取 值时,总有方案 1 优于方案 2;只有当 M(s1 ) 中的 i 取较小的值(如 i = - 0.5),而同时又让 M(s2 ) 中的 i 取较大的值(如 i = 0)时,会导致 M(s2 ) > M(s1 ) , 即方案 2 优于方案 1。 由此提示:在各方案综合评价 联系数中的 i 作不同步取值时,有可能引起各方案 综合评价值大小排序的变化,为此需要就各方案综 合评价联系数中的 i 作不同步取值时各方案排序问 题展开进一步的讨论和分析。 表 5 在不确定条件下的各方案综合评价值 Table 5 Comprehensive evaluation result of each scheme under the condition of uncertainty i = - 1 i = - 0.5 i = 0 i = 0.5 i = 1 M(s1 ) M(s2 ) M(s3 ) M(s4 ) M(s5 ) M(s6 ) 0.0091② -0.0231⑥ -0.0078④ -0.0215⑤ -0.0002③ 0.0470① 0.2663② 0.2056⑤ 0.2299④ 0.1549⑥ 0.2472③ 0.3113① 0.5237② 0.4342⑤ 0.4676④ 0.3313⑥ 0.4947③ 0.5756① 0.7809② 0.6629⑤ 0.7053④ 0.5077⑥ 0.7422③ 0.8299① 1.0382② 0.8915⑤ 0.9429④ 0.6840⑥ 0.9897③ 1.1042① 注:小圆圈内数字为综合评价值从大到小的排序号。 为了分析 i 不同步取值时方案排序的变化情 况,把 i = - 1 和 i = 1 这两种极端情况下的所有 64 种 排序进行统计,并按排名先后分别赋以 6、5、4、3、2、 1 的权值,求和得表 6。 表 6 两种极端情况下( i 不同步取值)各方案排名统计 Table 6 The rank statistics of each scheme under the two extreme cases (the value of i is not synchronized) 方案 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次 第 6 次 总分 1 2 3 4 5 6 Σ 16 2 4 1 8 33 64 18 8 12 5 16 5 64 8 12 12 10 12 10 64 12 8 12 10 12 10 64 8 3 16 20 12 5 64 2 31 8 18 4 1 64 272 161 208 159 240 304 1344 总分最高的为最优方案,最低的为最差方案。 可见,在 i 不同步取值情况下所得的排序结果与同 步情况下所得结果一致,即:方案 6>方案 1>方案 5> 方案 3>方案 2>方案 4。 6 结束语 当 vague 集中的不确定度 πv(x) ≠ 0 时,需要对 vague 集的不确定性展开分析,为此,本文给出把 vague 集转化为集对分析联系数,借助联系数中 i 的 不同取值展开不确定性分析的思路,并应用于一个 黑启动 vague 集决策实例,不仅给出了更为客观合 理的黑启动方案排序,也为利用 vague 集数据开展 不确定性分析提供了一种可行的途径;此外,文章还 给出了专家关联权重和指标关联权重向专家独立权 重与指标独立权重过渡的计算方法,对其他领域中 的类似决策也有一定参考作用。 第 5 期 赵玉铃,等:集对分析联系数在黑启动 vague 集决策中的应用研究 ·637·

·638. 智能系统学报 第9卷 参考文献: The method of transmission network flexible planning based on the connection number model [J].Proceedings of the [1]LINDENMEYER D,DOMMEL H W,ADIBI MM,Power CSEE,2006,43(12):16-20. system restoration-a bibliographical survey[J].Internation- [12]万官泉,张尧,汪穗峰.基于联系数的配电系统可靠性不 al Journal of Electrical Power and Energy Systems,2001,23 确定性评估[J].电力系统自动化,2008,32(4):31-34. (3):219-227. WAN Guanquan,ZHANG Yao,WANG Suifeng.Uncer- [2]THALE S,AGARWAL V.A smart control strategy for the tainty evaluation for distribution system reliability based on black start of a microgrid based on PV and other auxiliary connection number[J].Automation of Electric Power Sys- sources under islanded condition[Cl//37th IEEE Photovol- tems,2008,32(4):31-34. taie Specialists Conference.[S.1]:IEEE,2011:2454-2459. [13]陈卫东,肖先勇,陈礼频,等.考虑可靠性参数影响的电 [3]ADIBI MM,KAFKA L R J,MILANICZ D P.Expert sys- 压暂降频次联系数评估方法[J].中国电机工程学报, tem requirements for power system restoration [J].IEEE 2010,47(31):35-42. Trans on Power Systems,1994,9(3):1592-1598. CHEN Weidong,XIAO Xianyong,CHEN Lipin,et al. [4]林济铿,蒋越梅,岳顺民,等.基于DEA/AHP模型的电力 Connection number evaluation method of the voltage sag fre- 系统黑启动有效方案评估[J].电力系统自动化,2007,31 quency considered reliability parameters affection[].Pro- (15):65-69 ceedings of the CSEE,2010,47(31):35-42. LIN Jikeng,JIANG Yuemei,YUE Shunmin,et al.Assess- [14]安磊,王绵斌,谭忠富.基于集对故障树法的输变电工程 ment of effective schemes for power system blackstart based 风险评估模型[J].华东电力,2011,40(1):12-18. on EDA/AHP[J].Automation of Electric Power Systems, AN Lei,WANG Mianbin,TAN Zhongfu.The assessment 2007,31(15):65-69. model of power transmission project risk based on fault tree [5]ISLAM S,CHOWDHURY N.A case-base windows graphic analysis method[J].East China Electric Power,2011,40 package for the education and training of power system resto- (1):12-18. ration[J.IEEE Trans on Power Systems,2001,16(2): [15]刘俊华,罗隆福,张志文,等.基于模糊集对分析法的电 181-187 能质量综合评价[J].电网技术,2012,36(7):81-85. [6]刘伟佳,林振智,文福拴,等.基于直觉模糊距离的黑启动 LIU Junhua,LUO Longfu,ZHANG Zhiwen,et al.Com- 群体决策一致性分析与优化[J].电力系统自动化,2012, prehensive evaluation of power quality based on fuzzy set 36(10):1-6. pair analysis [J].Power System Technology,2012,36 LIU Weijia,LIN Zhenzhi,WEN Fushuan,et al.Consisten- (7):81-85. cy analysis and optimization of black-start decision consisten- [16]刘俊华,罗隆福,张志文,等.一种考虑排序稳定分析的 cy based on intutionistic fuzzy distanceJ.Automation of E- 电能质量综合评估新方法[J].中国电机工程学报, lectric Power Systems,2012,36(10):1-6. 2013,33(1):70-76 [7]曾顺奇,林振智,文福拴,等.基于vague集理论的黑启动 LIU Junhua,LUO Longfu,ZHANG Zhiwen,et al.A new 决策模型与方法[J].电力系统自动化,2011,35(2):18- method for power quality comprehensive evaluation consid- 22 ering the analysis of sequence stability[J].Proceedings of ZENG Shungi,LIN Zhenzhi,WEN Fushuan,et al.The the CSEE,2013.33(1):70-76. model and method of black-start decision based on the theory [17]刘秀梅,赵克勤.基于集对分析联系数的信息不完全直 of vague set[J].Automation of Electric Power Systems, 觉模糊多属性决策[J].数学的实践与认识,2010,40 2011,35(2):18-22. (1):67-77. [8]赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术 LIU Xiumei,ZHAO Keqin.Multiple attribute decision 出版社,2000:1-18. making with the incomplete information and intuitionistic [9]赵克勤.二元联系数A+Bi的理论基础和基本算法及在人 fuzzy number based on the connection number of set-pair a- 工智能中的应用J].智能系统学报,2008,3(6):16-22. nalysis[J].Mathematics in Practice and Theory,2010,40 [10]ZHAO Keqin.The two element connection number A+Bi (1):67.77 basic theory and algorithm and its application in artificial [18]BUSTINCE H,BURILLO P.vague sets are intuitionistic intelligence[J].CAAI Transactions on Intelligent Systems, fuzzy sets []]Fuzzy Sets and Systems,1996,79(3): 2008,3(6):16-22. 403-405. [11]金华征,程浩忠,杨晓梅,等.基于联系数模型的电网灵 [19]赵克勤.集对分析的不确定性系统理论在人工智能中的 活规划方法[J].中国电机工程学报,2006,43(12):16- 应用[J].智能系统学报,2006,1(2):18-25. 20. ZHAO Keqin.Application in artificial intelligence of uncer- JIN Huazheng,CHENG Haozhong,YANG Xiaomei,et al. tainty system theory of set-pair analysis[J].CAAI Transac-
参考文献: [1] LINDENMEYER D, DOMMEL H W, ADIBI M M, Power system restoration—a bibliographical survey[J]. Internation⁃ al Journal of Electrical Power and Energy Systems, 2001, 23 (3): 219⁃227. [2]THALE S, AGARWAL V. A smart control strategy for the black start of a microgrid based on PV and other auxiliary sources under islanded condition[C] / / 37th IEEE Photovol⁃ taic Specialists Conference. [S.1]:IEEE, 2011:2454⁃2459. [3]ADIBI M M, KAFKA L R J, MILANICZ D P. Expert sys⁃ tem requirements for power system restoration [ J ]. IEEE Trans on Power Systems, 1994, 9(3): 1592⁃1598. [4]林济铿,蒋越梅,岳顺民,等.基于 DEA/ AHP 模型的电力 系统黑启动有效方案评估[J].电力系统自动化,2007,31 (15):65⁃69. LIN Jikeng, JIANG Yuemei, YUE Shunmin, et al. Assess⁃ ment of effective schemes for power system blackstart based on EDA/ AHP[J] . Automation of Electric Power Systems, 2007, 31(15): 65⁃69. [5]ISLAM S, CHOWDHURY N. A case⁃base windows graphic package for the education and training of power system resto⁃ ration[ J]. IEEE Trans on Power Systems, 2001, 16( 2): 181⁃187. [6]刘伟佳,林振智,文福拴,等.基于直觉模糊距离的黑启动 群体决策一致性分析与优化[ J].电力系统自动化,2012, 36(10):1⁃6. LIU Weijia, LIN Zhenzhi, WEN Fushuan, et al. Consisten⁃ cy analysis and optimization of black⁃start decision consisten⁃ cy based on intutionistic fuzzy distance[J]. Automation of E⁃ lectric Power Systems, 2012, 36(10): 1⁃6. [7]曾顺奇,林振智,文福拴,等.基于 vague 集理论的黑启动 决策模型与方法[ J].电力系统自动化,2011,35(2):18⁃ 22. ZENG Shunqi, LIN Zhenzhi, WEN Fushuan, et al. The model and method of black⁃start decision based on the theory of vague set [ J]. Automation of Electric Power Systems, 2011, 35(2): 18⁃22. [8]赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术 出版社,2000:1⁃18. [9]赵克勤.二元联系数 A+Bi 的理论基础和基本算法及在人 工智能中的应用[J].智能系统学报,2008,3(6):16⁃22. [10]ZHAO Keqin. The two element connection number A+Bi basic theory and algorithm and its application in artificial intelligence[J]. CAAI Transactions on Intelligent Systems, 2008, 3(6): 16⁃22. [11]金华征,程浩忠,杨晓梅,等.基于联系数模型的电网灵 活规划方法[J].中国电机工程学报,2006,43( 12):16⁃ 20. JIN Huazheng, CHENG Haozhong, YANG Xiaomei, et al. The method of transmission network flexible planning based on the connection number model [ J]. Proceedings of the CSEE, 2006, 43(12): 16⁃20. [12]万官泉,张尧,汪穗峰.基于联系数的配电系统可靠性不 确定性评估[J].电力系统自动化,2008,32(4):31⁃34. WAN Guanquan, ZHANG Yao, WANG Suifeng. Uncer⁃ tainty evaluation for distribution system reliability based on connection number[J]. Automation of Electric Power Sys⁃ tems, 2008, 32(4): 31⁃34. [13]陈卫东,肖先勇,陈礼频,等.考虑可靠性参数影响的电 压暂降频次联系数评估方法[ J].中国电机工程学报, 2010,47(31):35⁃42. CHEN Weidong, XIAO Xianyong, CHEN Lipin, et al. Connection number evaluation method of the voltage sag fre⁃ quency considered reliability parameters affection[ J]. Pro⁃ ceedings of the CSEE, 2010, 47(31): 35⁃42. [14]安磊,王绵斌,谭忠富.基于集对故障树法的输变电工程 风险评估模型[J].华东电力,2011,40(1):12⁃18. AN Lei, WANG Mianbin, TAN Zhongfu. The assessment model of power transmission project risk based on fault tree analysis method[J]. East China Electric Power, 2011, 40 (1): 12⁃18. [15]刘俊华,罗隆福,张志文,等.基于模糊集对分析法的电 能质量综合评价[J].电网技术,2012,36(7):81⁃85. LIU Junhua, LUO Longfu, ZHANG Zhiwen, et al. Com⁃ prehensive evaluation of power quality based on fuzzy set pair analysis [ J ]. Power System Technology, 2012, 36 (7): 81⁃85. [16]刘俊华,罗隆福,张志文,等.一种考虑排序稳定分析的 电能质量综合评估新方法 [ J]. 中国电机工程学报, 2013,33(1):70⁃76 LIU Junhua, LUO Longfu, ZHANG Zhiwen, et al. A new method for power quality comprehensive evaluation consid⁃ ering the analysis of sequence stability[ J]. Proceedings of the CSEE, 2013, 33(1): 70⁃76. [17]刘秀梅,赵克勤.基于集对分析联系数的信息不完全直 觉模糊多属性决策[ J]. 数学的实践与认识,2010,40 (1):67⁃77. LIU Xiumei, ZHAO Keqin. Multiple attribute decision making with the incomplete information and intuitionistic fuzzy number based on the connection number of set⁃pair a⁃ nalysis[ J]. Mathematics in Practice and Theory,2010,40 (1):67⁃77. [18] BUSTINCE H, BURILLO P. vague sets are intuitionistic fuzzy sets [ J]. Fuzzy Sets and Systems, 1996, 79 ( 3): 403⁃405. [19]赵克勤.集对分析的不确定性系统理论在人工智能中的 应用[J].智能系统学报,2006,1(2):18⁃25. ZHAO Keqin. Application in artificial intelligence of uncer⁃ tainty system theory of set⁃pair analysis[J]. CAAI Transac⁃ ·638· 智 能 系 统 学 报 第 9 卷

第5期 赵玉铃,等:集对分析联系数在黑启动vgue集决策中的应用研究 639· tions on Intelligent Systems,2006,1(2):18-25. 7({c2,c3})=(0.37,0.43) [20]赵克勤.基于集对分析的不确定性多属性决策模型与算 W({c2,c4})=(0.5,0.3) 法[J刀.智能系统学报,2010,5(1):41-50. W({c3,c4})=(0.45,0.3) ZHAO Keqin.Application in artificial intelligence of uncer- W({c1,c3})=(0.35,0.45) tainty system theory of set-pair analysis[J].CAAI Transac- W({c1,c4})=(0.45,0.30) tions on Intelligent Systems,2010,5(1):41-50. W({c2,c3,c4})=(0.75,0.10) 作者简介: W({c1,c3,c4})=(0.75,0.10) 赵玉铃,女,1963年生,副教授,主 W({c1,c2,ca})=(0.68,0.15) 要研究方向为电子技术课程教学及建 W({c1,c2,c3})=(0.55,0.25) 设、电气技术应用、配电网安全运行,发 W({c1,c2,c3,c4})=(1.00,0.00) 表学术论文20余篇,出版教材4部。 专家e给出的指标权重如下: W({c1})=(0.2,0.5) W({c2})=(0.1,0.65) 张廉,男,1965年生,副教授,主要 W({c3})=(0.15,0.7) 研究方向为工程力学、电力传动的计算 W({c})=(0.15,0.7) 机控制与仿真,发表学术论文10余篇。 W({c1,c2})=(0.35,0.3) W({c2,c3})=(0.3,0.4) W({c2,c4})=(0.3,0.4) W({c3,c4})=(0.35,0.4) W({c1,c3})=(0.42,0.28) 附录专家e2与专家e给出的指标关联权重的计算 W({c1,c4})=(0.42,0.28) 专家e2给出的指标权重如下: W({c2,c3,c4})=(0.6,0.05) W({c1})=(0.15,0.7) W({c1,c3,c4})=(0.65,0.05) W({c2})=(0.2,0.7) W({c1,c2,c4})=(0.55,0.15) W({c3})=(0.15,0.7) W({c1,c2,c3})=(0.6,0.05) W({ca})=(0.25,0.55) W({c1,c2c3,c4})=(1.00,0.00) W({c1,c2})=(0.3,0.5) 专家e,与专家e,给出的指标关联权重联系数如附表。 专家,给出的黑启动指标关联权重联系数 专家 指标c1 指标c2 指标c3 指标ca 0.15+0.15i 0.2+0.1i 0.15+0.15i 0.25+0.2i 2(03+0.2) 2(03+02) 2(037+0.2) 2(05+0.2) a5+02 1 (037+0.2) a5+025 2045+025 2(045+0.250) (0.5+0.2) 1 (0.35+02) 1 (045+0250) 1 3(075+0.15) 3075+015 3(075+0.150) 3(0.75+0.150) 3(068+0.17m 3(068+0.17m 3(0.75+0150) 号075+015 号05+029 号05+02) 号(05+029 3(068+017m 子:+侧 1+侧 1+a 41+时 (0.2013+0.0810i)× 平均权重 (0.2119+0.0716i)× (0.2085+0.0802i)× (0.2409+0.0883i)× 联系数 (0.34575+0.0625i)= (0.34575+0.0625i)= (0.34575+0.0625i)= (0.34575+0.0625i)= 0.0696+0.0457i 0.0733+0.0425i 0.0721+0.0457i 0.0833+0.0510i
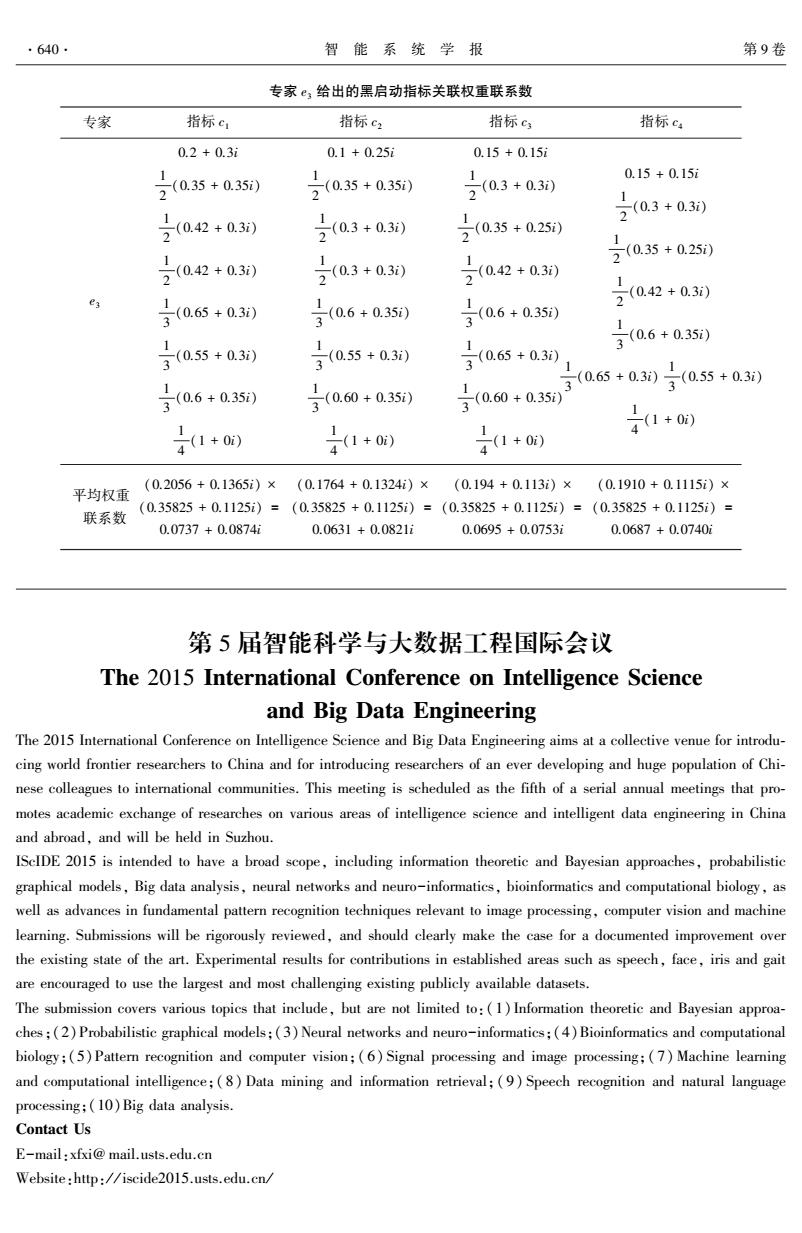
tions on Intelligent Systems, 2006, 1(2): 18⁃25. [20]赵克勤.基于集对分析的不确定性多属性决策模型与算 法[J].智能系统学报,2010,5(1):41⁃50. ZHAO Keqin. Application in artificial intelligence of uncer⁃ tainty system theory of set⁃pair analysis[J]. CAAI Transac⁃ tions on Intelligent Systems, 2010, 5(1): 41⁃50. 作者简介: 赵玉铃,女,1963 年生,副教授,主 要研究方向为电子技术课程教学及建 设、电气技术应用、配电网安全运行,发 表学术论文 20 余篇,出版教材 4 部。 张廉,男,1965 年生,副教授,主要 研究方向为工程力学、电力传动的计算 机控制与仿真,发表学术论文 10 余篇。 附录 专家 e2 与专家 e3 给出的指标关联权重的计算 专家 e2 给出的指标权重如下: W( c1 { } ) = (0.15,0.7) W( c2 { } ) = (0.2,0.7) W( c3 { } ) = (0.15,0.7) W( c4 { } ) = (0.25,0.55) W( c1 ,c2 { } ) = (0.3,0.5) W( c2 ,c3 { } ) = (0.37,0.43) W( c2 ,c4 { } ) = (0.5,0.3) W( c3 ,c4 { } ) = (0.45,0.3) W( c1 ,c3 { } ) = (0.35,0.45) W( c1 ,c4 { } ) = (0.45,0.30) W( c2 ,c3 ,c4 { } ) = (0.75,0.10) W( c1 ,c3 ,c4 { } ) = (0.75,0.10) W( c1 ,c2 ,c4 { } ) = (0.68,0.15) W( c1 ,c2 ,c3 { } ) = (0.55,0.25) W( c1 ,c2 ,c3 ,c4 { } ) = (1.00,0.00) 专家 e3 给出的指标权重如下: W( c1 { } ) = (0.2,0.5) W( c2 { } ) = (0.1,0.65) W( c3 { } ) = (0.15,0.7) W( c4 { } ) = (0.15,0.7) W( c1 ,c2 { } ) = (0.35,0.3) W( c2 ,c3 { } ) = (0.3,0.4) W( c2 ,c4 { } ) = (0.3,0.4) W( c3 ,c4 { } ) = (0.35,0.4) W( c1 ,c3 { } ) = (0.42,0.28) W( c1 ,c4 { } ) = (0.42,0.28) W( c2 ,c3 ,c4 { } ) = (0.6,0.05) W( c1 ,c3 ,c4 { } ) = (0.65,0.05) W( c1 ,c2 ,c4 { } ) = (0.55,0.15) W( c1 ,c2 ,c3 { } ) = (0.6,0.05) W( c1 ,c2 ,c3 ,c4 { } ) = (1.00,0.00) 专家 e2 与专家 e3 给出的指标关联权重联系数如附表。 专家 e2 给出的黑启动指标关联权重联系数 专家 指标 c1 指标 c2 指标 c3 指标 c4 e2 0.15 + 0.15i 1 2 (0.3 + 0.2i) 1 2 (0.35 + 0.2i) 1 2 (0.45 + 0.25i) 1 3 (0.75 + 0.15i) 1 3 (0.68 + 0.17i) 1 3 (0.55 + 0.2i) 1 4 (1 + 0i) 0.2 + 0.1i 1 2 (0.3 + 0.2i) 1 2 (0.37 + 0.2i) 1 2 (0.5 + 0.2i) 1 3 (0.75 + 0.15i) 1 3 (0.68 + 0.17i) 1 3 (0.55 + 0.2i) 1 4 (1 + 0i) 0.15 + 0.15i 1 2 (0.37 + 0.2i) 1 2 (0.45 + 0.25i) 1 2 (0.35 + 0.2i) 1 3 (0.75 + 0.15i) 1 3 (0.75 + 0.15i) 1 3 (0.55 + 0.2i) 1 4 (1 + 0i) 0.25 + 0.2i 1 2 (0.5 + 0.2i) 1 2 (0.45 + 0.25i) 1 2 (0.45 + 0.25i) 1 3 (0.75 + 0.15i) 1 3 (0.75 + 0.15i) 1 3 (0.68 + 0.17i) 1 4 (1 + 0i) 平均权重 联系数 (0.2013 + 0.0810i) × (0.34575 + 0.0625i) = 0.0696 + 0.0457i (0.2119 + 0.0716i) × (0.34575 + 0.0625i) = 0.0733 + 0.0425i (0.2085 + 0.0802i) × (0.34575 + 0.0625i) = 0.0721 + 0.0457i (0.2409 + 0.0883i) × (0.34575 + 0.0625i) = 0.0833 + 0.0510i 第 5 期 赵玉铃,等:集对分析联系数在黑启动 vague 集决策中的应用研究 ·639·
.640. 智能系统学报 第9卷 专家给出的黑启动指标关联权重联系数 专家 指标c1 指标c2 指标c 指标c4 0.2+0.3i 0.1+0.25i 0.15+0.15i 2(0.35+0.350) (0.35+0,35i) 1 2(0.3+0.30) 0.15+0.15i (03) a3+a刘 2(0.3+0.3) ≥3(0.35+0.25i) (0.42+03) 子a3+03刘 042+0.3) 1 2(0.35+0.250 号065+03 号06+0350) 号a6+0350 a2+a3动 3(0.6+0.35i)) 号0s5+03 05+03) 吉065+030 号(06+035列 号(00+035 g060+035 3(Q65+03刘号(055+0.3) 子1+侧 子1+0 子1+a) 1+侧 (0.2056+0.1365i)×(0.1764+0.1324i)× (0.194+0.113i)× (0.1910+0.1115i)× 平均权重 (0.35825+0.1125i)=(0.35825+0.1125i)=(0.35825+0.1125i)=(0.35825+0.1125i)= 联系数 0.0737+0.0874i 0.0631+0.0821i 0.0695+0.0753i 0.0687+0.0740i 第5届智能科学与大数据工程国际会议 The 2015 International Conference on Intelligence Science and Big Data Engineering The 2015 International Conference on Intelligence Science and Big Data Engineering aims at a collective venue for introdu- cing world frontier researchers to China and for introducing researchers of an ever developing and huge population of Chi- nese colleagues to international communities.This meeting is scheduled as the fifth of a serial annual meetings that pro- motes academic exchange of researches on various areas of intelligence science and intelligent data engineering in China and abroad,and will be held in Suzhou. IScIDE 2015 is intended to have a broad scope,including information theoretic and Bayesian approaches,probabilistic graphical models,Big data analysis,neural networks and neuro-informatics,bioinformatics and computational biology,as well as advances in fundamental pattern recognition techniques relevant to image processing,computer vision and machine learning.Submissions will be rigorously reviewed,and should clearly make the case for a documented improvement over the existing state of the art.Experimental results for contributions in established areas such as speech,face,iris and gait are encouraged to use the largest and most challenging existing publicly available datasets. The submission covers various topics that include,but are not limited to:(1)Information theoretic and Bayesian approa- ches;(2)Probabilistic graphical models;(3)Neural networks and neuro-informatics;(4)Bioinformatics and computational biology;(5)Pattern recognition and computer vision;(6)Signal processing and image processing;(7)Machine learning and computational intelligence;(8)Data mining and information retrieval;(9)Speech recognition and natural language processing;(10)Big data analysis. Contact Us E-mail:xfxi@mail.usts.edu.cn Website:http://iscide2015.usts.edu.cn/
专家 e3 给出的黑启动指标关联权重联系数 专家 指标 c1 指标 c2 指标 c3 指标 c4 e3 0.2 + 0.3i 1 2 (0.35 + 0.35i) 1 2 (0.42 + 0.3i) 1 2 (0.42 + 0.3i) 1 3 (0.65 + 0.3i) 1 3 (0.55 + 0.3i) 1 3 (0.6 + 0.35i) 1 4 (1 + 0i) 0.1 + 0.25i 1 2 (0.35 + 0.35i) 1 2 (0.3 + 0.3i) 1 2 (0.3 + 0.3i) 1 3 (0.6 + 0.35i) 1 3 (0.55 + 0.3i) 1 3 (0.60 + 0.35i) 1 4 (1 + 0i) 0.15 + 0.15i 1 2 (0.3 + 0.3i) 1 2 (0.35 + 0.25i) 1 2 (0.42 + 0.3i) 1 3 (0.6 + 0.35i) 1 3 (0.65 + 0.3i) 1 3 (0.60 + 0.35i) 1 4 (1 + 0i) 0.15 + 0.15i 1 2 (0.3 + 0.3i) 1 2 (0.35 + 0.25i) 1 2 (0.42 + 0.3i) 1 3 (0.6 + 0.35i) 1 3 (0.65 + 0.3i) 1 3 (0.55 + 0.3i) 1 4 (1 + 0i) 平均权重 联系数 (0.2056 + 0.1365i) × (0.35825 + 0.1125i) = 0.0737 + 0.0874i (0.1764 + 0.1324i) × (0.35825 + 0.1125i) = 0.0631 + 0.0821i (0.194 + 0.113i) × (0.35825 + 0.1125i) = 0.0695 + 0.0753i (0.1910 + 0.1115i) × (0.35825 + 0.1125i) = 0.0687 + 0.0740i 第 5 届智能科学与大数据工程国际会议 The 2015 International Conference on Intelligence Science and Big Data Engineering The 2015 International Conference on Intelligence Science and Big Data Engineering aims at a collective venue for introdu⁃ cing world frontier researchers to China and for introducing researchers of an ever developing and huge population of Chi⁃ nese colleagues to international communities. This meeting is scheduled as the fifth of a serial annual meetings that pro⁃ motes academic exchange of researches on various areas of intelligence science and intelligent data engineering in China and abroad, and will be held in Suzhou. IScIDE 2015 is intended to have a broad scope, including information theoretic and Bayesian approaches, probabilistic graphical models, Big data analysis, neural networks and neuro-informatics, bioinformatics and computational biology, as well as advances in fundamental pattern recognition techniques relevant to image processing, computer vision and machine learning. Submissions will be rigorously reviewed, and should clearly make the case for a documented improvement over the existing state of the art. Experimental results for contributions in established areas such as speech, face, iris and gait are encouraged to use the largest and most challenging existing publicly available datasets. The submission covers various topics that include, but are not limited to:(1) Information theoretic and Bayesian approa⁃ ches;(2)Probabilistic graphical models;(3)Neural networks and neuro-informatics;(4)Bioinformatics and computational biology;(5)Pattern recognition and computer vision;(6) Signal processing and image processing;(7) Machine learning and computational intelligence;( 8) Data mining and information retrieval;( 9) Speech recognition and natural language processing;(10)Big data analysis. Contact Us E-mail:xfxi@ mail.usts.edu.cn Website:http: / / iscide2015.usts.edu.cn / ·640· 智 能 系 统 学 报 第 9 卷