
Basic Electronics Introductory Lecture Course for Technology and Instrumentation in Particle Physics 2011 Chicago,Illinois June9-14,2011 Presented By Gary Drake Argonne National Laboratory Session 2
Presented By Gary Drake Argonne National Laboratory Basic Electronics Introductory Lecture Course for Technology and Instrumentation in Particle Physics 2011 Chicago, Illinois June 9-14, 2011 Session 2

Session 2 Time-Varying Signals Circuits Basic Electronics-Special Lecture for TIPP 2011 2 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 2 Gary Drake, Argonne National Lab – Session 2 Session 2 Time-Varying Signals & Circuits
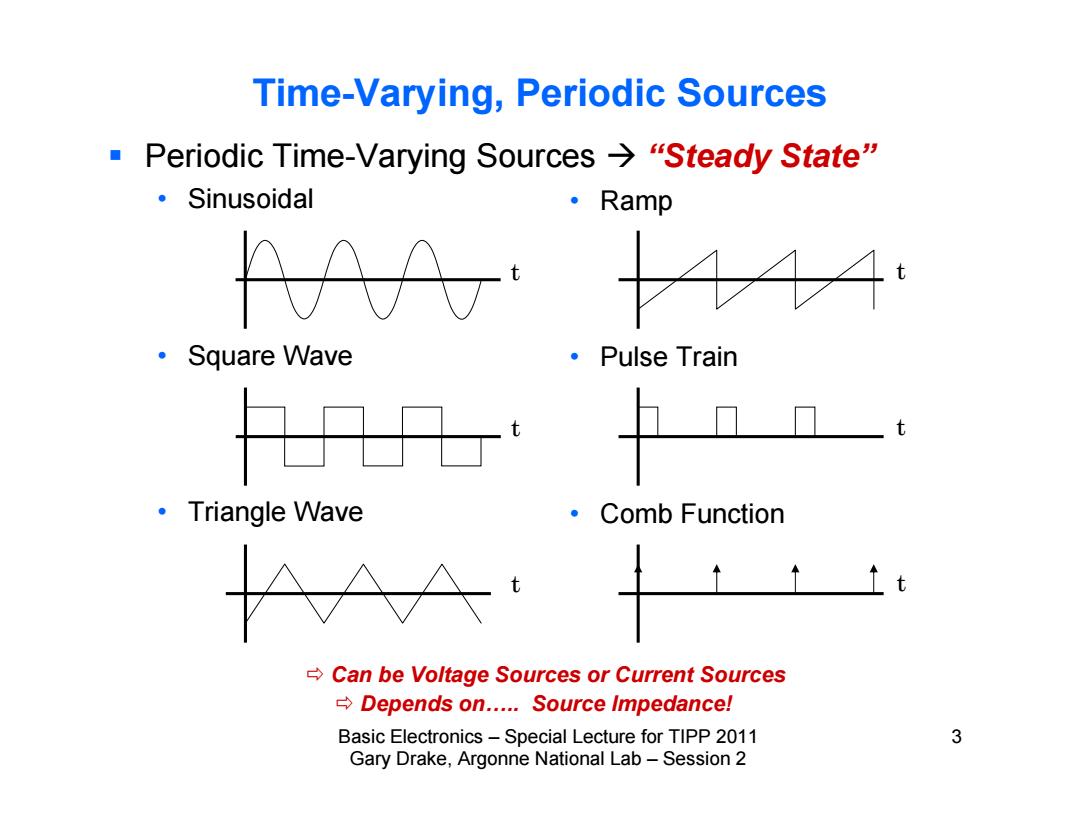
Time-Varying,Periodic Sources ·Periodic Time-Varying Sources→“Steady State” ·Sinusoidal ·Ramp ·Square Wave ·Pulse Train + 。.Triangle Wave ·Comb Function ↑t Can be Voltage Sources or Current Sources Depends on.....Source Impedance! Basic Electronics-Special Lecture for TIPP 2011 3 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 3 Gary Drake, Argonne National Lab – Session 2 Time-Varying, Periodic Sources Periodic Time-Varying Sources “Steady State” • Sinusoidal • Square Wave • Triangle Wave • Ramp • Pulse Train • Comb Function t t t t t t Can be Voltage Sources or Current Sources Depends on….. Source Impedance!

Sinusoidal Sources ■Sinusoidal Sources ·Characterized by frequency(o=2πf,phaseΦ,period T(T=l/fD, and peak amplitude Vp ∀ vo(t)=Vp sin(ot+φ) Is the average value important? VAwe=lT∫vo)dt=l/T∫Vp sin(t)dt=0→Wo,not really.. ·We often use the“Effective Value,”or RMS Vr=V1n∫o2e)dt=√1/n∫Vp2sin2otdt =Vp/V2 →This IS useful. Basic Electronics-Special Lecture for TIPP 2011 images from Wikipedia 4 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 4 Gary Drake, Argonne National Lab – Session 2 Sinusoidal Sources • Characterized by frequency f), phase , period (T = 1 / f), and peak amplitude Vp • Is the average value important? • We often use the “Effective Value,” or RMS VEFF = e 1/T f vO2(t) dt = e 1/T f VP2 sin2(t) dt = VP / S 2 Sinusoidal Sources t VAVG = 1/T f vO(t) dt = 1/T f VP sin(t) dt = 0 0 T vO(t) = VP sin(t + ) VP T -VP Images from Wikipedia 0 T 0 T No, not really… 0 T This IS useful…

Resistive Circuits with Steady State Sources Consider again a resistive network,but this time with a sinusoidal source What is the instantaneous power consumed by R? p()=V()i1() V1(t) Vp sin(@t)[Vp sin(@t)]/RI =[V,2/R]sin2(o。t) V3(t) What is the average power consumed by R? PAvG=1/TPi(t)dt v(t)=V。sin(oot) =1/T [Vp2/R]sin2(t)dt PAVG=VP2/R1 Just as before,we can use Kirchoff's Laws: VEFF2 R1,since VEPF=Vp/V2 In general, i(t)R1-V(t)=0 i(t)=V()/R1 PAVG=VEFF IEFF vo(t)=vs(t) Says that Effective Values of a sinusoid produce average power equivalent to comparable DC values Basic Electronics-Special Lecture for TIPP 2011 5 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 5 Gary Drake, Argonne National Lab – Session 2 Resistive Circuits with Steady State Sources Consider again a resistive network, but this time with a sinusoidal source vs(t) = Vp sin( t) Just as before, we can use Kirchoff’s Laws: i1(t) R1 – vs(t)= 0 i1(t) = vs(t) / R1 vO(t) = vS(t) v1(t) vs(t) What is the instantaneous power consumed by R1? p1(t) = v1(t) i1(t) = Vp sin(o t) [Vp sin(o t)] / R1 = [Vp2 / R1] sin2(o I1 t) R1 What is the average power consumed by R1? PAVG = 1/T f p1(t) dt = 1/T f [VP2/R1] sin2(o t) dt PAVG = ½ VP2 / R1 = VEFF2 / R1, since VEFF = VP / S2 In general, PAVG = VEFF IEFF 0 T 0 T Says that Effective Values of a sinusoid produce average power equivalent to comparable DC values
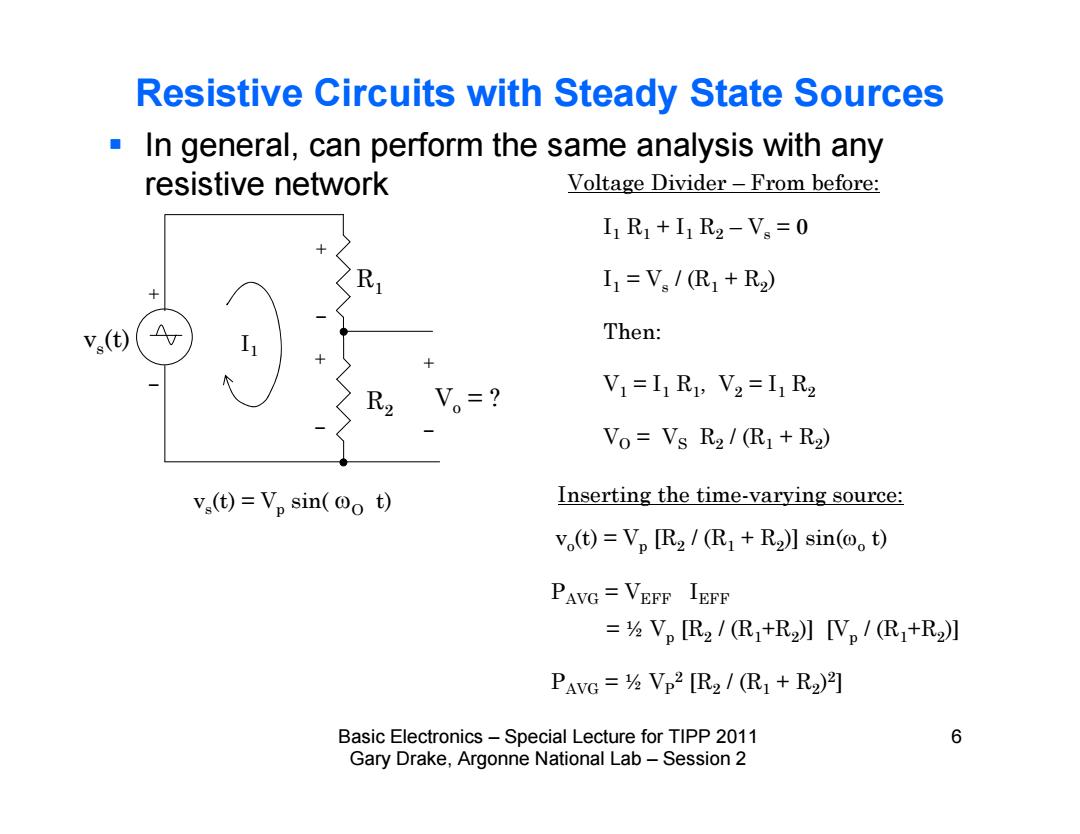
Resistive Circuits with Steady State Sources In general,can perform the same analysis with any resistive network Voltage Divider-From before: I1R1+I1R2-V。=0 I1=V/R1+R2) v(t) Then: V1=I1R1,V2=I1R2 Vo=Vs R2/(R1+R2) vs(t)=Vp sin(@o t) Inserting the time-varying source: v。(t)=VpR2/(R1+R2】sin(o。t) PAVG VEFF IEFF =⅓V,R2/R1+R2】V。/(R+R2] PAVG =Vp2 [R2 /(R1+R2)2] Basic Electronics-Special Lecture for TIPP 2011 6 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 6 Gary Drake, Argonne National Lab – Session 2 Resistive Circuits with Steady State Sources In general, can perform the same analysis with any resistive network vs(t) = Vp sin( t) Voltage Divider – From before: R1 R2 Vo = ? I1 vs(t) I1 R1 + I1 R2 – Vs = 0 I1 = Vs / (R1 + R2) Then: V1 = I1 R1, V2 = I1 R2 VO = VS R2 / (R1 + R2) Inserting the time-varying source: vo(t) = Vp [R2 / (R1 + R2)] sin(o t) PAVG = VEFF IEFF = ½ Vp [R2 / (R1+R2)] [Vp / (R1+R2)] PAVG = ½ VP2 [R2 / (R1 + R2)2]
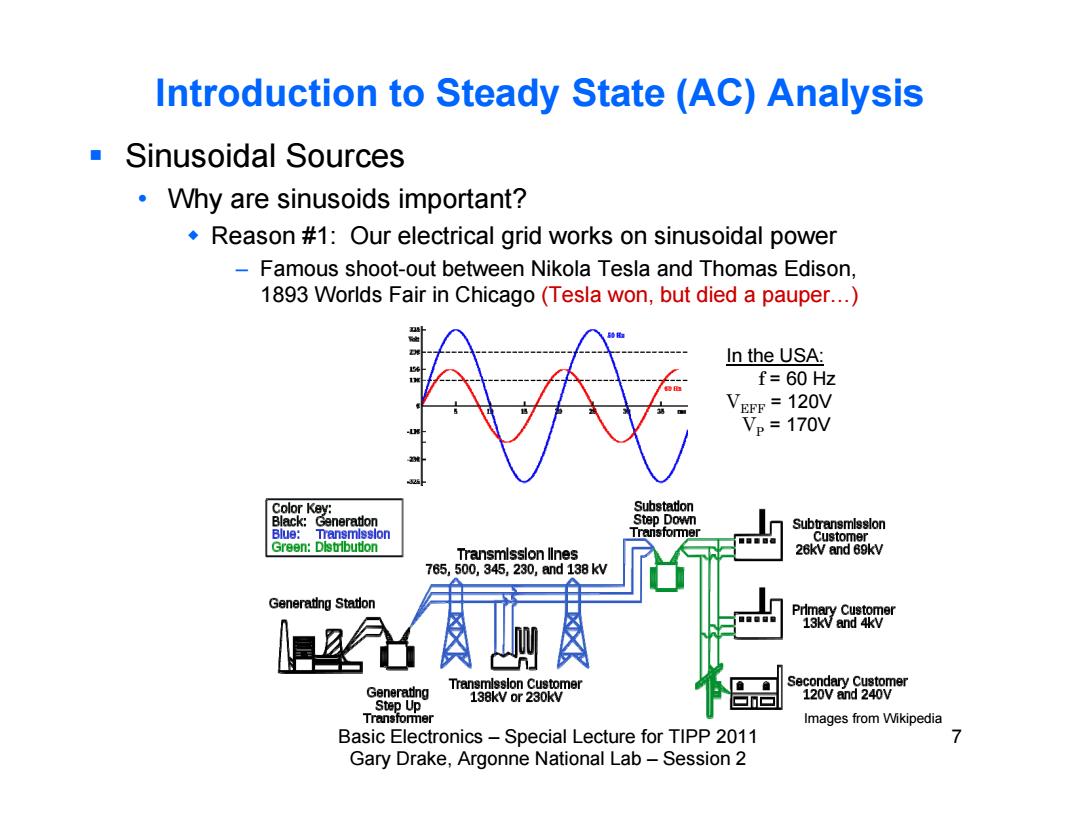
Introduction to Steady State (AC)Analysis ■ Sinusoidal Sources Why are sinusoids important? Reason #1:Our electrical grid works on sinusoidal power Famous shoot-out between Nikola Tesla and Thomas Edison, 1893 Worlds Fair in Chicago (Tesla won,but died a pauper...) In the USA: f=60 Hz VEFF=120V Vp 170V Color Key: Substaton Black: Generaton Step Down Subtransmlsslon Blue: Transmlsslon Transfommer Customer Green:Distrbution Transmlsslon llnes 26kV and 69kV 765,500,345,230,and138kW Generadng Staton Prlmary Customer 13kV and 4kV Generating Transmlsslon Customer Secondary Customer 138kV or 230kV 120V and 240V Step Up ▣▣ Transformer Images from Wikipedia Basic Electronics-Special Lecture for TIPP 2011 7 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 7 Gary Drake, Argonne National Lab – Session 2 Introduction to Steady State (AC) Analysis Sinusoidal Sources • Why are sinusoids important? Reason #1: Our electrical grid works on sinusoidal power – Famous shoot-out between Nikola Tesla and Thomas Edison, 1893 Worlds Fair in Chicago (Tesla won, but died a pauper…) In the USA: f = 60 Hz VEFF = 120V VP = 170V Images from Wikipedia

Introduction to Steady State (AC)Analysis Sinusoidal Sources (Continued) Why are sinusoids important(Cont.)? Reason #2:Convenient representation in the Freguency Domain Time Domain Magnitude Frequency Domain 0 00 Angle 0 v(t)=VP cos(oot+φo) Define phasors:F(@)=Mag Angle If:v(t)=Vp cos(@ot+)Phasor form:V(@)=Vp/o Has connection with Complex Number Analysis...More on this later Basic Electronics-Special Lecture for TIPP 2011 8 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 8 Gary Drake, Argonne National Lab – Session 2 Introduction to Steady State (AC) Analysis Sinusoidal Sources (Continued) • Why are sinusoids important (Cont.)? Reason #2: Convenient representation in the Frequency Domain • Define phasors: t v(t) = VP cos(Ot + O) VP T -VP VP O O Time Domain Frequency Domain Phasor form: V() = VP O Magnitude Angle If: v(t) = VP cos(Ot + O) F() = Mag Angle Has connection with Complex Number Analysis… More on this later

Introduction to Steady State (AC)Analysis Sinusoidal Sources (Continued) Why are sinusoids important (Cont.)? Reason #3:Any periodic waveform can be represented as an infinite sum of sinusoids,with frequencies that are multiples of the fundamental frequency 0o>Fourier Series For any periodic waveform V(t),with fundamental frequency oo 00=(2π)/T v(t)=>E edino.),where j=v-1 The coefficients E are given by: T/2 E=1/T/V(t)e-inoot dt -T/2 n@o are the harmonic frequencies of v(t) Basic Electronics-Special Lecture for TIPP 2011 9 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 9 Gary Drake, Argonne National Lab – Session 2 Introduction to Steady State (AC) Analysis Sinusoidal Sources (Continued) • Why are sinusoids important (Cont.)? Reason #3: Any periodic waveform can be represented as an infinite sum of sinusoids, with frequencies that are multiples of the fundamental frequency O Fourier Series – For any periodic waveform V(t), with fundamental frequency O – The coefficients En are given by: t v(t) = En e(jnot) , where j = S -1 n=-h +h T O = (2 ) / T En = 1/T f V(t) e-jnot dt -T/2 T/2 v(t) n0 are the harmonic frequencies of v(t)

Introduction to Steady State (AC)Analysis Sinusoidal Sources (Continued) Why are sinusoids important(Cont.) Example:Fourier Series of a Square Wave Time Domain Frequency Domain 2Vp/π -70 7a0 90 00=(2)/T 十 Vo=∑EeGno.t) wherej=v-1 n=-00 n=-o where E=(2Vp/nπ)sin(nπ/2) Notice that only the odd harmonics of v(t)are present in this particular example... Basic Electronics-Special Lecture for TIPP 2011 10 Gary Drake,Argonne National Lab-Session 2
Basic Electronics – Special Lecture for TIPP 2011 10 Gary Drake, Argonne National Lab – Session 2 Introduction to Steady State (AC) Analysis Sinusoidal Sources (Continued) • Why are sinusoids important (Cont.)? Example: Fourier Series of a Square Wave where En = (2VP / n) sin(n / 2) 2VP / O Time Domain Frequency Domain t VP VP O O O O O O O O O V(t) = En e(jnot) n=-h +h T O = (2 ) / T Notice that only the odd harmonics of v(t) are present in this particular example… where j = S -1 n=-h +h