
试卷代号:1002 座位号■■ 中央广播电视大学2008一2009学年度第一学期“开放本科”期末考试(半开卷)》 计算机数学基础(1) 试题 2009年1月 题号 二 三 四 总 分 分数 得 分 评卷人 一、单项选择题(每小题4分,共20分) 得分 1. 设P:张国益生病了,Q:张国益出差了.R:我同意他不参加学习.则命题“只有张 国益生病了或出差了,我才同意他不参加学习”符号化的结果为(). A.PVQ→R B.R-(PVQ) C.P∧Q+R D.R-(PAQ) 得分☐2.设P,Q为两个命题,P→Q的真值为0.当且仅当P,Q的赋值为( A.(0,0) B.(0,1) C.(1,0) D.(1,1) 得分☐3.设集合A=1,2,3,4,R是A上的二元关系,其关系矩阵为M®= 10017 1000 则R的关系表达式是(). 0001 L1000j A.{,,,,} B.{,,,,】 C.{,,,,》 D.{,,,,} 7
试卷代号:1002 座位号!二习 中央广播电视大学2008-2009学年度第一学期“开放本科”期末考试(半开卷) 计算机数学基础(1) 试题 2009年 1月 题 号 四 总 分 分 数 4 ft !I一 ‘’小题‘分’共2。分’ 匣王口1·设“:张国益生病了,Q:张国益出差了.*:我同意他不参加学习.则命题“只有张 国益生病了或出差 了 A. P V Q-R C. P A Q->R ,我才同意他不参加学习”符号化的结果为( B. R- (P VQ) D. R- (P AQ) 匣到二」2·设尸,Q为两个命题,P-Q的真值为。.当且仅当尸,Q的赋值为( (0,0) (1,0) B. (0,1) D. (1,1) A C 匣死口3·设集合A一{1, 2 , 3 , 4 } ,*是A上的二元关系,其关系矩阵为、 一 L1 0 )0 一 0- A.{ , , , , } B.{, , , ,} C.{ , , ,‘ 1,4> } n.{ , , , , }

得分 4. 设集合A={1,2,3,4},A上的偏序关系R的关系图如图1所示,那么偏序集 的哈斯图是(). 图 0 4 420 3 20 B. c D. 得分 5.以下命题正确的是( A.n(n≥l)阶完全图K.都是欧拉图 B.n(n≥1)阶完全图K,都是哈密顿图 C.n(n≥5)阶完全图K.都是平面图 D.连通且满足m=n一1的图(V|=n,|E1=m)是树 得 分 评卷人 二、填空题(每小题4分,共20分) 得分 6- 设A,B为任意命题公式,C为重言式,若A∧C白B∧C,那么A+B是 式(重言式、矛盾式或满足式). 得分 1- 设F(x):x是鸟,G(x):x会飞翔.则命题“鸟会飞”符号化为 得分 8. 设A,B,C是三个集合,若ACB且C≠,则有AXC BXC. 得分 9. 无向完全图K的所有非同构生成子图有个 得分 10.数组{1,2,3,4,4}是一个能构成无向简单图的度数序列,此命题的真值是
pit州 卜设集合A=(1,2,3,4),A上的偏序关系R的关系图如图1所示,都么偏序集 的哈斯图是( ) 乞 厂 书 知 犷 夕 D. 针 丫 ,J 1站 C 4 腻 。 k%州 卜 21 A 以 . A 下 . n 命 (n 题 ) 正 l) 确 阶 的 完 是 全 ( 图K二都是欧 R。拉图 B. n(nll)阶完全图K,都是哈密顿图 C. n(n)5)阶完全图 K,都是平面图 D.连通且满足 m=n-1的图(I V I =n, I EI =m)是树 是 , 是 B 一 值 杆 一 真 A - 的 么 一 心 题 邓 - 以 命 滩 一 -B 此 C - - 门 ︿ | - - 贝 B 伪 - 序 幼 讹 - 蜘 0 号 c… 别 竹 符 冲 个. 够 曰 . 产 A: - 的 I A :). 飞 争 一 图 创 若 试 会 峰 一 翔 巧 八 足 鸟 ,Nl - 秘 20 式 洲 卿 乙 ﹂犯 简 铆 ︷协 勃 题 狡 清 向 洪 暗 树 胡 半 图 到 分 重 貂 赊 抓 子 助 州 为 循 I.j 且 成 礴 卜 ︺勺 矛 翔 B 打 构 崛 ,C 饥 形 创 她 脚 *,J 式 ﹂韵 会 A 酬 个 林 公 勤 汉 若 泪 一 傲 题 搜 r)= △中 春 是 空 对 式 (x 豁 和 日 眺 命 -夕 只 集 所 针 旗 黔 一 ,G 怜 蒯 ,4 .︸ 一门介 一 .鸟 二 一 3 4 一一 唯 - 卿 赘 凡 3, 为 - 七 准 图 2, 一 川 C 生 ‘以 B - )= l,( 全 1, ﹁1 -r es J 卜 一 (x ,B 完 1{: 一、 一 一 A 一 叹 气 朽 组 -人 一 - " 一 厂 月 向 挂 -卷 - - 设 - 没 比 到 数
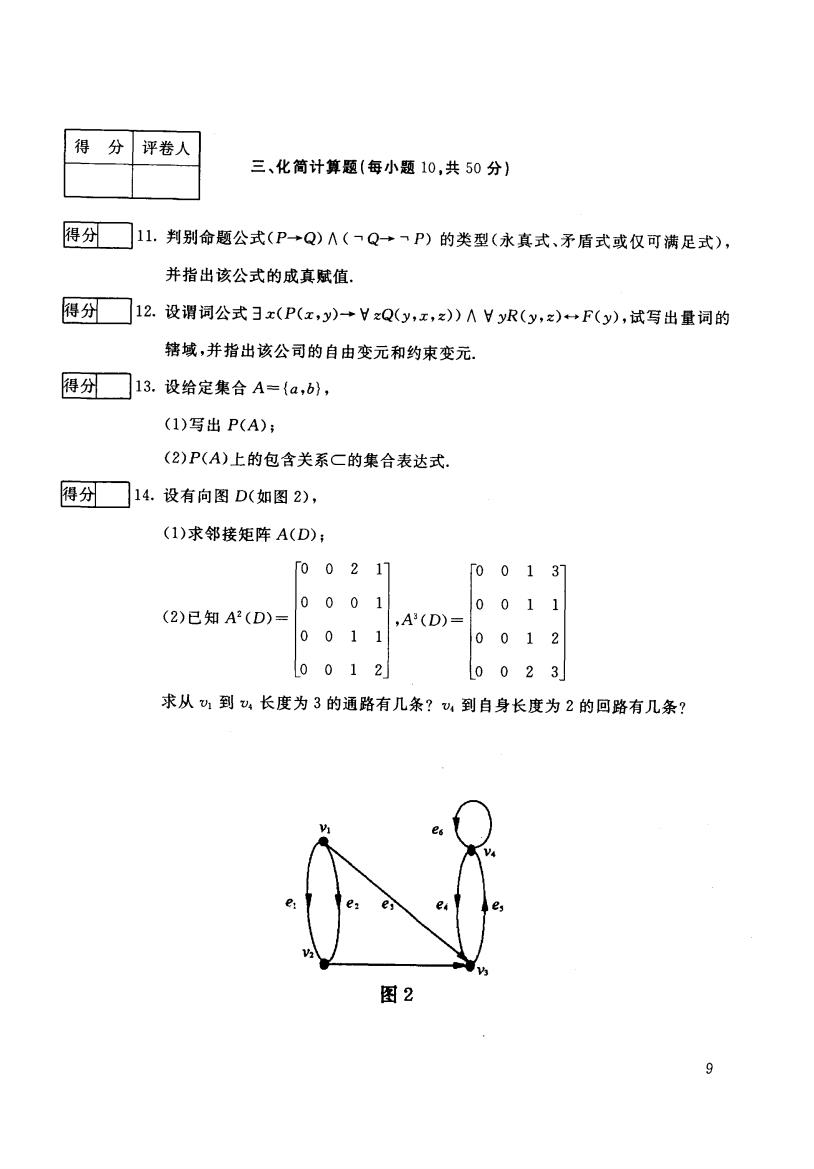
得 分 评卷人 三、化简计算题(每小题10,共50分) 得分 11. 判别命题公式(P+Q)八(一Q→一P)的类型(永真式、矛盾式或仅可满足式), 并指出该公式的成真赋值。 得分 12. 设谓词公式]x(P(x,y)+HxQ(y,x,z)∧yR(y,z)+F(y),试写出量词的 辖域,并指出该公司的自由变元和约束变元. 得分 13.设给定集合A={a,b}, (1)写出P(A); (2)P(A)上的包含关系C的集合表达式. 得分 14.设有向图D(如图2), (1)求邻接矩阵A(D); 「00217 001 > 0001 001 1 (2)已知A2(D)= ,A3(D)= 0011 0012 0012」 002 3 求从到4长度为3的通路有几条?,到自身长度为2的回路有几条? 图2 9
得 分 评卷人 三 、化简计算题(每小题 10,共 50分) 匣三二}11.删命题公式(P-Q) A(,Q-.,尸)的类型(永真式、矛盾式或仅可满足式) 0州 }12. FS州 }13. I4-州 }14. 并指出该公式的成真赋值. 设谓词公式3x(P(x,y)- V zQ(y,x,z)) A `d yR(y,z)HF(y),试写出量词的 辖域 ,并指出该公司的 自由变元和约束变元. 设给定集合 A二{a, b}, (1)写出 P(A) ; (2)P(A)上的包含关系C的集合表达式. 设有向图D(如图2), (1)求邻接矩阵 A(D); A D -- ﹁l es eses les l es es l l l lt l 0 2 1 0 0 1 (2)已知 A'(D)= 0 1 1 0 1 2 0 1 0 1 0 1 0 2 求从 VI到 v;长度为 3的通路有几条?v;到自身长度为 2的回路有几条? e: 1 下e2 e; 图2

得分州 15. 设图G(如图3表示)是6个结点a,b,c,d,e,f的图,试求图G的最小生成树,并 计算它的权. 23 25 28 图3 得分 评卷人 四、证明题(本题共10分) 得分 16. 假设R是非空集合A上的等价关系,证明R的逆关系R-1也是A上的等价关 系 10
匣王口15·设图G(如图3表示)是6个结点。,b,c,d,e,,的图,试求图G的剔生成树,并 计算它的权. 得 分 评卷人 四、证明题(本题共 10分) 匝三口16.假设*。空集合A上的等价关系,证明*的逆关系*一也是A上的等价关

试卷代号:1002 中央广播电视大学2008一2009学年度第一学期“开放本科”期末考试(半开卷) 计算机数学基础(1)试题答案及评分标准 (供参考) 2009年1月 一、单项选择题(每小题4分,共20分)】 1.B 2.C 3.A 4.C 5.D 二、填空题(每小题4分,共20分)】 6.重言 7.Yx(F(z)-G(x)) 8.二 9.4 10.0 三、化简计算题(每小题10分,共50分)】 11.(P→Q)A(Q+P)台(PVQ)A(QVP)=PVQ (4分) 所以,(P→Q)∧(一Q→一P)是仅可满足式 (8分) 该公式的成真赋值:(0,0),(0,1),(1,1) (10分) 或利用真值表法,可参照给分 12.了x的辖域是:P(x,y)→H2Q(y,x,z); Hx的辖域是:Q(y,x,z): Vy的辖域是:R(v,x) (6分) 公式的自由变元是:P(x,y)→HzQ(y,x,z)中的y,R(y,x)中的x,F(y)中的y;约束变 元是:R(x,y)→HzQ(y,xz)中的x、,R(y,x)中的y. (10分) 13.P(A)={,{a},{b},{a,b}} (4分) C={,,,,}(10分) 11
试卷代号:1002 中央广播电视大学2008-2009学年度第一学期“开放本科”期末考试(半开卷) 计算机数学基础(1) 试题答案及评分标准 (供参考) 2009年 1月 一、单项选择题(每小题 4分,共 20分) 1. B 2. C 3. A 4. C 5.D 二、填空题(每小题 4分,共 20分) .重言 .Vx(F(x)一 G(x)) 8. c 9. 4 10. 0 三、化简计算题 (每小题 10分 ,共 50分) 11.(P-Q) A(,Q--,P)#}(,PV Q)A(QV,P)=,PVQ (4分) 所以,(尸~Q)八(,Q~ ,尸)是仅可满足式. (8分) 该公式的成真赋值:(0,0), , ,,} (10分) 11

14.(1) 「021 01 001 0 A(D)= (5分) 0 001 0011 (2)从到山长度为3的通路有3条,到自身长度为2的回路2条 (10分) 15.构造连通无圈的图,即最小生成树,用克鲁斯克尔算法: 第一步:取ab=1;第二步:取af=4;第三步:取fe=3;第四步:取ad=9;第五步:取bc=23 (6分) 图4 如图4.权为1+4+3+9+23=40 (10分) 四、证明题(本题共10分) 16.(1)Hx∈A,则∈R,显然∈R-1,R-1具有自反性. (2分) (2)Hx,y∈A,如果∈R-1台∈R →∈R(R是对称的)台∈RI, R具有对称性. (5分) (3)Hx,y,z∈A,如果∈R-1∧∈R- 台∈R∧∈R台∈R∧∈R →∈R(R是传递的)台R-1, R具有传递性、 (8分) 总之,R是等价关系. (10分) 12
14.(1) A(D)二 2 1 0 1 0 0 0 1 (5分) (2)从 v:到 v,长度为 3的通路有 3条,v,到自身长度为 2的回路 2条. (1。分) 15.构造连通无圈的图,即最小生成树,用克鲁斯克尔算法: 第一步:取ab=1;第二步:取a f}-4;第三步:取fe=3;第四步:取 ad=9;第五步:取be=23 (6分) 如图4.权为1+4+3+9+23=40 (10分) 四、证明题(本题共 10分) 16. (1)VxCEA,则ER,显然 E R-' , R-‘具有自反性. (2分) (2) V x,yEA,如果 E R-' }# E R =}>ER(R是对称的)a E R-', R-‘具有对称性. (5分) (3) V x, y,zEA,如果ER-' AER-' #}ERA ER#} ER八 E R zz>ER(R是传递的)K'R-', R具有传递性. (8分) 总之,R是等价关系. (10分)