
试卷代号:1024 座位号■■ 中央广播电视大学2008一2009学年度第一学期“开放本科”期末考试 信号处理原理 试题 2009年1月 题 号 一 二 三 四 五 六 总 分 分 数 得 分 评卷人 一、判断题(每小题3分,共15分) 1.Sa函数是奇函数。 2.直流信号的傅立叶频谱是阶跃函数。 3.拉普拉斯变换满足线性性。 4.时不变系统的响应与激励施加的时刻无关。 5.单位阶跃序列的Z变换结果是常数。 得分 评卷人 二、单项选择题(每小题5分,共25分) 1.图解法求卷积所涉及的操作有() A.采样、量化、相乘 B.反褶、平移、相乘(积分) C.编码、传输、解码 D.相乘、取对数、相加 182
试卷代号:1024 座位号二 口 中央广播电视大学2008-2009学年度第一学期“开放本科”期末考试 信号处理原理 试题 2009年 1月 题 号 四 五 六 总 分 分 数 得 分 评卷人 一、判断题(每小题 3分,共 15分) Sa函数是奇 函数。 2.直流信号的傅立叶频谱是阶跃函数。 3.拉普拉斯变换满足线性性。 4.时不变系统 的响应与激励施加的时刻无关。 5.单位阶跃序列的 Z变换结果是常数。 得 分 评卷人 二、单项选择题(每小题 5分,共 25分 ) 1.图解法求卷积所涉及 的操作有( A.采样、量化、相乘 B.反褶 、平移、相乘 (积分) C.编码 、传输 、解码 D.相乘 、取对数、相加 182

2.下面关于信号的分解,描述不正确的是() A.直流分量和交流信号 B.确定分量与不确定分量 C.偶分量与奇分量 D.实部分量与虚部分量 3.奇周期信号的傅立叶级数含有() A.余弦项和直流项 B.正弦项 C.正弦项和直流项 D.余弦项 4.单位冲激信号的拉氏变换结果是() A.0 B.1 ci D.-1 5.双边序列ZT的ROC是(.) A.有限的几个点 B.圆形区域 C.圆外区域 D.环形区域 得 分 评卷人 三、填空题(每小题4分,共20分) 2.任一个函数f(t)与信号6(t一to)的卷积等于 3.傅里叶变换的线性特性,包含两部分: 和 4.Z[2u(n)+8(n)]= 5.一个序列是因果序列的充分必要条件是: ;一个序列 是反因果序列的充分必要条件是 183
2.下面关于信号的分解 ,描述不正确的是( A.直流分量和交流信号 B.确定分量与不确定分量 C.偶分量与奇分量 D.实部分量与虚部分量 3.奇周期信号的傅立叶级数含有( ) A.余弦项和直流项 B.正弦项 C.正弦项和直流项 D.余弦项 4.单位冲激信号的拉氏变换结果是( ) A.0 C.生 B. 1 D. 一 1 5.双边序列 ZT的 ROC是( 有限的几个点 圆外 区域 圆形 区域 环形 区域 得 分 评卷人 三、填空题 (每小题 4分 ,共 20分} 1.{几f(t)S(‘一3)dt-— 。 2.任一个函数 f(t)与信号8(t-to)的卷积等于 3·傅里叶变换的线性特性,包含两部分:_ 4. Z[2u(n)+8(n)]= 5.一个序列是因果序列的充分必要条件是: ;一个 序列 是反因果序列的充分必要条件是 183
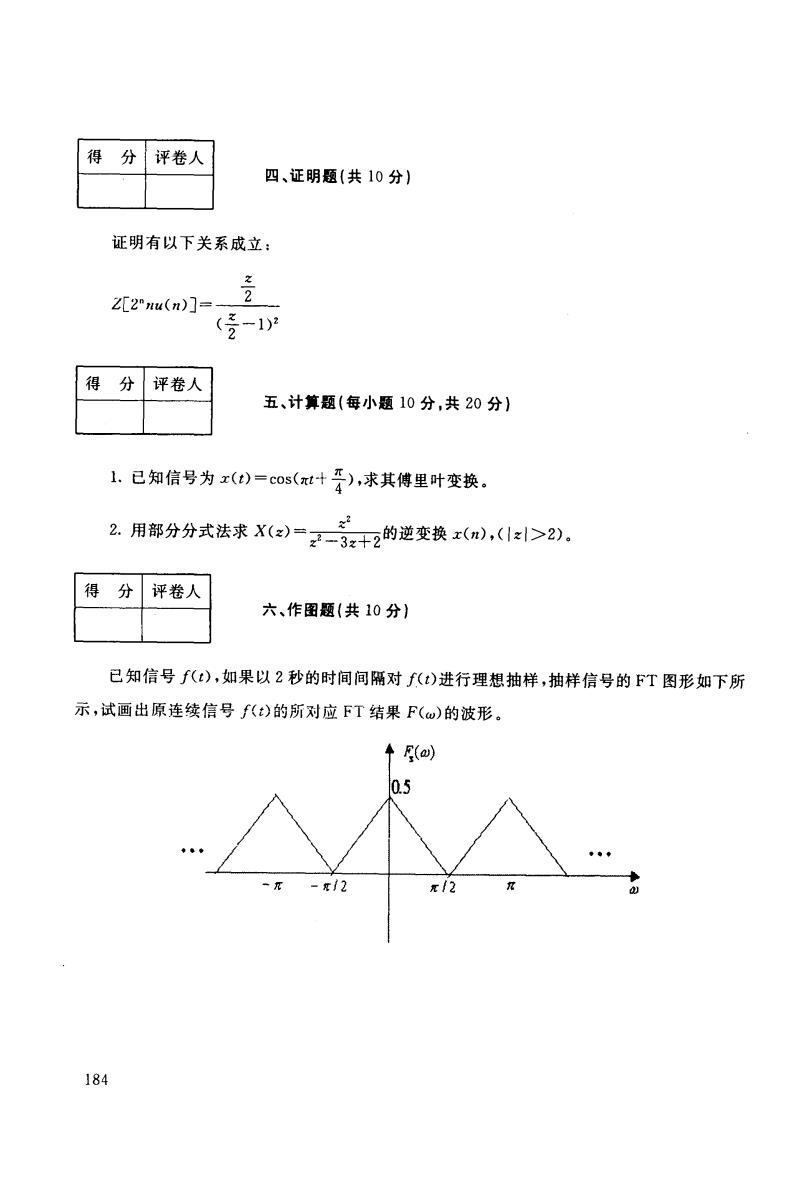
得分 评卷人 四、证明题(共10分】 证明有以下关系成立: 2 Z[2u(n)]=- 2 -1 得 分 评卷人 五、计算题(每小题10分,共20分】 1.已知信号为x()=cos(x+牙),求其傅里叶变换。 2.用部分分式法求X()=2-3十2的逆变换x(m),(>2). 得 分 评卷人 六、作图题(共10分) 已知信号f(t),如果以2秒的时间间隔对f(t)进行理想抽样,抽样信号的FT图形如下所 示,试画出原连续信号f(t)的所对应FT结果F(w)的波形。 F(a) 0.5 -π/2 184
得 分 评卷人 四、证明题(共 10分) 证明有以下关系成立 z ,二。、。 , 、, 2 Z仁2"nu(n)J=一一.一二二一-一 (三一1)2 2 - 得 分 评卷人 五、计算题(每小题 10分,共 20分) ·已知信号为二(t) =Cos(二‘十晋,,求其傅里叶变换。 。用部分分式法求X(二)一了 艺 一井0 z不-了一 ‘ 的逆变换二(。),(}二}>2), 得 分 评卷人 六、作图题(共 10分) 已知信号f(t),如果以2秒的时间间隔对f(t)进行理想抽样,抽样信号的FT图形如下所 示,试画出原连续信号 f (t)的所对应 FT结果 F(co)的波形。 184

试卷代号:1024 中央广播电视大学2008一2009学年度第一学期“开放本科”期末考试 信号处理原理 试题答案及评分标准 (供参考) 2009年1月 、判断题(每小题3分,共15分) 1.错误 2.错误 3.正确 4.正确 5.错误 二、单项选择题(每小题5分,共25分) 1.B 2.B 3.B 4.B 5.D 三、填空题(每小题4分,共20分) 1.f(3) 2.f(t-to) 3.齐次性 叠加性 4.321 x-1 5.x(n)=x(n)·u(n) x(n)=x(n)·u(-n-1) 四、证明题(共10分) 证明有以下关系成立: Z[2"nu(n)]= (2-1)2 证明:根据定义:La“x(n)j= ,∑4x()z -盒m() =x() (5分) 185
试卷代号:1024 中央广播电视大学2008-2009 信号处理原理 学年度第一学期“开放本科”期末考试 试题答案及评分标准 (供参考) 2009年 1月 一、判断题(每小题 3分,共 15分) 1.错误 2.错误 3.正确 4.正确 5.错误 二、单项选择题 (每小题 5分,共 25分) 1.B 2.B 3.B 三、填空题(每小题 4分,共 20分) 1. f(3) 2. f (t一to) 3.齐次性 叠加性 4. B 5.D 3z一 1 z一 1 5. x(n)=x(n)·u(n) 四、证明题 (共 10分 ) 证 明有以下关系成立: x(n) =x(n)·u(一n一1) 。二n。 , 、二 2 乙LL一nuln)j=— 么一1)Z }下 证明:根据定义 :Gnu"xln月 = (5分 ) 185

X(z)=Z[z(m)]=Z[nu(n)]=(1) 所以Z孔2nu(n)]=X(z/2)= 经-10 (5分) 五、计算题(每小题10分,共20分】 1.已知信号为x()=cos(xt+),求其傅里叶变换。 解:x()=cos(rt+王) (neWem) (5分) 利用(对偶性)傅里叶变换关系式e'台2π6(w一h),得 X(w)=π[e46(w一π)+eiW“6(ω十x)] (5分) 2.用部分分式法求X(e)=2-32+2的逆变换x(m),(z>2) 解:把X(x)化成两个分式相乘: X(x)=z-(2-2 利用部分分式法展开为: X-22÷ (5分) 因为≈>2,所以x(n)是因果序列,所以x()是因果序列,于是 x(n)=(2m+1-1)u(n) (5分) 六、作图题(共10分) 答案: ◆F() -π12 π12 (10分) 186
而 X(z)=Z[x(n)〕二Z[nu(n)〕二 z (z一1)2 z 所以Z[2"nu(n)〕二X(二/2)一 止匕一 (菩 乙 一1)Z (5分) 五、计算题(每小题 10分,共20分) 已知信号为x (t) =cos(二,十手 侍 ),求其傅里叶变换。 解 : x(t’一cos(二‘+晋, 一喜 乙 (ejx/4 ejxt+。一jx/4 e-jxt) (5分) 利用(对偶性)傅里叶变换关系式of t a2,r8C。一。。),得 X (co)=二〔ejx/4 S(。一二)+。一j,/4 8(&j+二)〕 (5分) 2.用部分分式法求 X(z)二 z2 z2一3z+2的逆变换 x(n),(IzI>2) 解:把 X(z)化成两个分式相乘: X(之)= z2 (z一1) (z一2) 利用部分分式法展开为 : X(之)= z一2 z一 1 因为 !划 >2,所以 二(,:)是因果序列 ,所以 x(n)二(2n+’一1)u(n) 六、作图题(共 10分) 答案: (5分 ) x(n)是因果序列,于是 (5分 ) F(nl), (10分) 186