
2013-3-6 Chapter 4 Control Volume Analysis Learning Outcomes Demonstrate understanding of key concepts related to control volume analysis including distinguishing between steady-state and transient analysis,distinguishing between mass flow rate and volumetric flow rate,and the meanings of one-dimensional flow and flow work. Apply mass and energy balances to control volumes. 4-2
2013-3-6 1 Chapter 4 Control Volume Analysis Learning Outcomes ►Demonstrate understanding of key concepts related to control volume analysis including distinguishing between steady-state and transient analysis, distinguishing between mass flow rate and volumetric flow rate, and the meanings of one-dimensional flow and flow work. ►Apply mass and energy balances to control volumes. 4-2

2013-3-6 Learning Outcomes,cont. Develop appropriate engineering models for control volumes,with particular attention to analyzing components commonly encountered in engineering practice such as nozzles, diffusers,turbines,compressors,heat exchangers,throttling devices,and integrated systems that incorporate two or more components. Use property data in control volume analysis appropriately. 4-3 Conservation of mass Conservation of mass:Mass,like energy,is a conserved property,and it cannot be created or destroyed during a process. Closed systems(implicitly used):The mass of the system remain constant during a process. Control volumes:Mass can cross the boundaries and so we must keep track of the amount of mass entering and leaving the control volume. 2kg H2 + 16kg 18kg 02 H20 Mass is conserved even during chemical reactions Mass m and energy E equivalence E=mc where c=speed of light in vacuum 108
2013-3-6 2 Learning Outcomes, cont. ►Develop appropriate engineering models for control volumes, with particular attention to analyzing components commonly encountered in engineering practice such as nozzles, diffusers, turbines, compressors, heat exchangers, throttling devices, and integrated systems that incorporate two or more components. ►Use property data in control volume analysis appropriately. 4-3 Conservation of mass Mass is conserved even during chemical reactions. ►Conservation of mass: Mass, like energy, is a conserved property, and it cannot be created or destroyed during a process. ►Closed systems (implicitly used): The mass of the system remain constant during a process. ►Control volumes: Mass can cross the boundaries, and so we must keep track of the amount of mass entering and leaving the control volume. Mass m and energy E equivalence where c = speed of light in vacuum (c = 2.9979 × 108 m/s) The mass change due to energy change is negligible
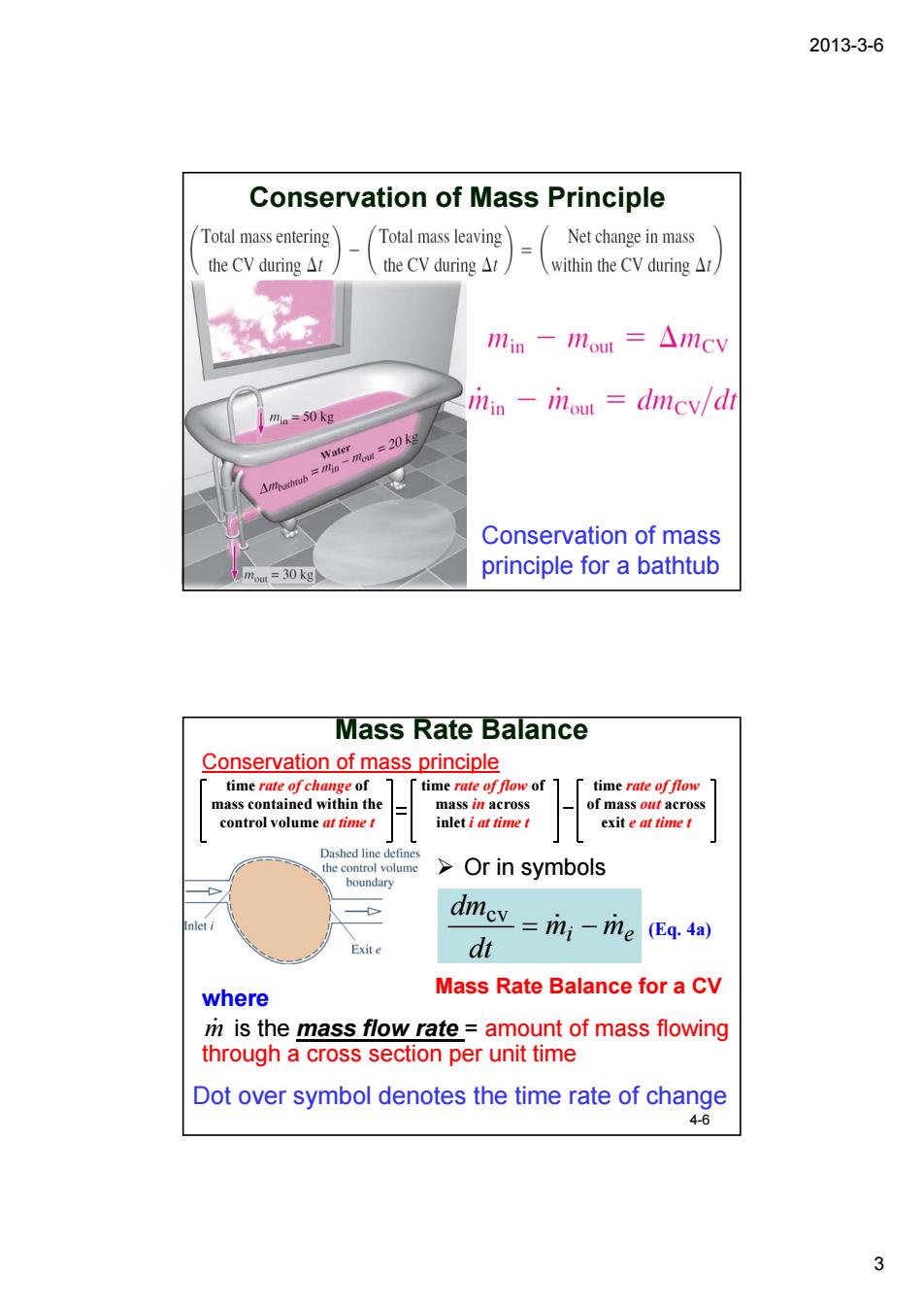
2013-3-6 Conservation of Mass Principle Total mass entering Total mass leaving Net change in mass the CV during△t 、the CV during△i, (within the CV during△r 1in-1mout=△11cy mn=50kg min -mou dmcv/dt =风=20 Conservation of mass :30 kg principle for a bathtub Mass Rate Balance Conservation of mass principle time rate offlow control volume me inleti at timet exit e at timet Dashed line >Or in symbols me (Eq.4a) dt where Mass Rate Balance for a CV ri is the mass flow rate=amount of mass flowing through a cross section per unit time Dot over symbol denotes the time rate of change 4-6 3
2013-3-6 3 Conservation of Mass Principle Conservation of mass principle for a bathtub Mass Rate Balance 4-6 time rate of change of mass contained within the control volume at time t time rate of flow of mass in across inlet i at time t time rate of flow of mass out across exit e at time t mi me dt dm = & − & cv (Eq. 4a) Mass Rate Balance for a CV where is the mass flow rate = amount of mass flowing through a cross section per unit time m& Dot over symbol denotes the time rate of change Conservation of mass principle ¾ Or in symbols

2013-3-6 Mass Rate Balance In practice there may be several locations on the boundary through which mass enters or exits. and its are accounted for by introducing summations: d=∑m-∑m44w dt The above equation represents the mass rate balance for control volumes with several inlets and exits. Total mass contained in CV at time t is so we can(v d d pdW=∑m-∑m 47 Mass Rate Balance-Integral Form The mass flow rate written in integral from is amount of mass Volyme crossing dA during p(v Ar)dA pV dA the time interval△t fluid The general comass can be written as ,pw=(pva)-(pv,dA d Or more general d p(.元)dA = d 元=unit vector More about this in Fluid Dynamics! 48 g
2013-3-6 4 Mass Rate Balance = ∑ −∑ e e i mi m dt dm & & cv (Eq. 4b) The above equation represents the mass rate balance for control volumes with several inlets and exits. ►In practice there may be several locations on the boundary through which mass enters or exits. Multiple inlets and exits are accounted for by introducing summations: 4-7 ►Total mass contained in CV at time t is so we can write Mass Rate Balance- Integral Form 4-8 ►The general conservation of mass can be written as Or more general ►The mass flow rate written in integral from is Æ Distance travelled by fluid Volume = unit vector More about this in Fluid Dynamics! Divide by Δt and integrate over area

2013-3-6 Mass Flow Rate (One-Dimensional Flow) Flow is normal to the boundary at locations where mass enters or exits the control volume All intensive properties are uniform with position over each inlet or exit area(A) through which matter flows. Mi=PAV=AV (Eq.4c) 7) where V is velocity_(not volume v is specific volume 49 Mass Rate Balance (Steady-State Form) Steady-state:all properties are unchanging in time For steady-state control volume,di/dt=0. ∑m;=∑me 1 (Eq.4d) mass rate mass rate OUT For single stream (one input one output) devices:nozzles,turbines,compressors,pumps m=m。 or VA=,A Steady Incompressible flow(single stream) most liquids VA=V24 4-10 5
2013-3-6 5 Mass Flow Rate (One-Dimensional Flow) ►Flow is normal to the boundary at locations where mass enters or exits the control volume. ►All intensive properties are uniform with position over each inlet or exit area (A) through which matter flows. v AV m& = ρAV = (Eq. 4c) where V is velocity (not volume) v is specific volume 4-9 ►For single stream (one input & one output) devices: nozzles, turbines, compressors, pumps: ►Steady Incompressible flow (single stream) Æ most liquids Mass Rate Balance (Steady-State Form) ►Steady-state: all properties are unchanging in time ►For steady-state control volume, dmcv / dt = 0. (Eq. 4d) mass rate IN mass rate OUT 4-10 or ∑ = ∑ e e i m&i m& V1A1 =V2A2 mi me & = & ρ1 V1A1 = ρ 2 V2A2

2013-3-6 Question Geometry Effects on Fluid Flow An incompressible liquid flows through the pipe shown in the fiqure.The velocity at location 2 is (choose one): 20 D iquid 1A=A,3 SOLUTION m=p护 2= pV=pV, 户= 2=4 4-11 us0oas8Pa90n8ti8iy Volumetric flow rate =A. 1 V dA. VMass flow i=pVavs Ac (kg/s) in =pV= rate The average velocity V is The volume flow defined as the average speed rate is the volume Cross section through a cross section. of fluid flowing through a cross section per u .12 6
2013-3-6 6 Question Geometry Effects on Fluid Flow An incompressible liquid flows through the pipe shown in the figure. The velocity at location 2 is (choose one): 2 1 Incompressible Liquid 2D D 1 2 1 2 in out Inlets Outlets m V m m V V V V ρ ρ ρ = = = = ∑ ∑ & & & & & & & & 11 2 2 2 1 1 21 1 2 2 2 2 2 1 21 1 2 2 1 / 4 / 4 2 4 AV A V A D VV V A D D D VVV D D V V π π = = = ⎛ ⎞ ⎛ ⎞ = = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ = r r r r r r r r r r 4-11 SOLUTION The average velocity Vavg is defined as the average speed through a cross section. No slip condition Use average velocity Mass flow rate Volumetric flow rate The volume flow rate is the volume of fluid flowing through a cross section per unit time. 4-12

2013-3-6 Sample problem .2 Liquid propane enters an initially empty cylindrical storage tank at a mass flow rate of 10 kg/s.Flow continues until the tank is filled with propane at 20C.9 bar.The tank is 25-m long and has a 4-m diameter.Determine the time,in minutes, to fill the tank Solution 0 dme=m- Separate variables and integrate between 0 and final time tmal -Read v for p=9 bar and T=20C 4-13 Sample problem .2 Liquid propane enters an initially empty cylindrical storage tank at a mass flow rate of 10 kg/s.Flow continues until the tank is filled with propane at 20C.9 bar.The tank is 25-m long and has a 4-m diameter.Determine the time,in minutes to fill the tank. Detailed Solution An initally-empty stereje tank ir hilled with qurd propane at a constant mars flow mtc.State data and tank dimentionr arc provided. 4-14 7
2013-3-6 7 Sample problem 4-13 = ∑ − ∑ e e i mi m dt dm & & cv 0 Solution - Separate variables and integrate between 0 and final time tfinal - Read v for p=9 bar and T = 20°C - Calculate tfinal Sample problem 4-14 Detailed Solution

2013-3-6 Solution EN长IM21W6 0DEL ANALYSIS: -4 +mcv6)=名:tf G) 4-15 Solution v66o C.99/)g EquaKmCi)jives =262wn io k3/s 4-16 8
2013-3-6 8 Solution 4-15 Solution 4-16

2013-3-6 eReview:Energy Balance for a Closed System Review:Closed Sys.Energy Balance The energy concepts introduced thus far are summarized in words as follows: change in the amount net amount of energy net amount of energy of energy contained trans rred in acros the time interval time interval Using previously defined symbols,this can be expressed as:E2-E1=Q-W Alternatively,△KE+△PE+△U=Q-W Be aware of the signs!A minus sign appears before w because energy transfer by work from the system to the surrounding is taken as positive 4-18 9
2013-3-6 9 Review: Energy Balance for a Closed System http://bcs.wiley.com/he-bcs/Books?action=index&itemId=0470918012&bcsId=6606 ►The energy concepts introduced thus far are summarized in words as follows: change in the amount of energy contained within a system during some time interval net amount of energy transferred in across the system boundary by heat transfer during the time interval net amount of energy transferred out across the system boundary by work during the time interval ►Using previously defined symbols, this can be expressed as: E2 – E1 = Q – W ►Alternatively, ΔKE + ΔPE + ΔU = Q – W Be aware of the signs! A minus sign appears before W because energy transfer by work from the system to the surrounding is taken as positive. 4-18 Review: Closed Sys. Energy Balance

2013-3-6 Review:Energy Rate Balance for CS The energy balance can be written in differential form as dE 60-8W The time rate form of the closed system energy balance is dE =Q-币 dt The rate form expressed in words is et rate contained withi transferred in the syste 4-19 Energy Rate Balance for CV, Comparina a control volume to a clos ed system: also ha ve energy that is carried in and out by the mass crossing its boundary ime rate of nge et rate at which net rate of energy of the en d ou the control volume by heat transfer by wo mass floving For one-inlet one-exit CV with one dir nsional flow =Q-巾+m,(+ g=i)-ite(ue+ +g)E4e) nergy o 10
2013-3-6 10 ►The rate form expressed in words is time rate of change of the energy contained within the system at time t net rate at which energy is being transferred in by heat transfer at time t net rate at which energy is being transferred out by work at time t ►The time rate form of the closed system energy balance is Q W dt dE & & = − 4-19 Review: Energy Rate Balance for CS ►The energy balance can be written in differential form as Energy Rate Balance for CV 4-20 ) 2 V ) ( 2 V ( 2 2 cv e e i e e i Q W mi ui gz m u gz dt dE = − + & + + − & + + & & (Eq. 4e) time rate of change of the energy contained within the control volume at time t net rate at which energy is being transferred in by heat transfer at time t net rate at which energy is being transferred out by work at time t net rate of energy transfer into the control volume accompanying mass flow ►Comparing a control volume to a closed system: we also have energy that is carried in and out by the mass crossing its boundary ►For one-inlet one-exit CV with one dimensional flow Rate of transfer of internal, kinetic and potential energy of entering/exiting streams