
第十二章网络函数和频率特性 前两章讨论了正弦激励频率为给定值时,动 态电路的正弦稳态响应。本章讨论正弦激励频率 变化时,动态电路的特性 一频率特性。为此, 先介绍在正弦稳态条件下的网络函数。然后利用 网络函数研究几种典型RC电路的频率特性。最后 介绍谐振电路及其频率特性。动态电路的频率特 性在电子和通信工程中得到了广泛应用,常用来 实现滤波、选频、移相等功能
第十二章 网络函数和频率特性 前两章讨论了正弦激励频率为给定值时,动 态电路的正弦稳态响应。本章讨论正弦激励频率 变化时,动态电路的特性——频率特性。为此, 先介绍在正弦稳态条件下的网络函数。然后利用 网络函数研究几种典型RC电路的频率特性。最后 介绍谐振电路及其频率特性。动态电路的频率特 性在电子和通信工程中得到了广泛应用,常用来 实现滤波、选频、移相等功能

§12-1网络函数 一、网络函数的定义和分类 动态电路在频率为的单一正弦激励下,正弦稳态响 应(输出)相量与激励(输入)相量之比,称为正弦稳态的网络 函数,记为H(Gw),即 输出相量 H(j@) (12-1) 输入相量 输入(激励)是独立电压源或独立电流源,输出(响应)是 感兴趣的某个电压或电流
§12-1 网络函数 一 、网络函数的定义和分类 (j ) (12-1) 输入相量 输出相量 H 输入(激励)是独立电压源或独立电流源,输出(响应)是 感兴趣的某个电压或电流。 动态电路在频率为ω的单一正弦激励下,正弦稳态响 应(输出)相量与激励(输入)相量之比,称为正弦稳态的网络 函数,记为H(jω),即

若输入和输出属于同一端口, 称为驱动点函数,或策动点函数。 No 以图示双口网络为例 0,1i,和02/i2 称为驱动点阻抗。 图12-1 i,1U和i21U2 称为驱动点导纳。 若输入和输出属于不同端口时,称为转移函数。 0211和0,112 称为转移阻抗。 i21U,和i1U2 称为转移导纳。 U21U1和U11U2 称为转移电压比。 121i1和1,1i2 称为转移电流比
U 1 / I 1 和 U 2 / I 2 称为驱动点阻抗。 若输入和输出属于同一端口, 称为驱动点函数,或策动点函数。 以图示双口网络为例 I 1 /U 1 和 I 2 /U 2 称为驱动点导纳。 若输入和输出属于不同端口时,称为转移函数。 2 1 U / I 和 U 1 / I 2 称为转移阻抗。 I 2 /U 1 和 I 1 /U 2 称为转移导纳。 U 2 /U 1 和 U 1 /U 2 称为转移电压比。 I 2 / I 1 和 I 1 / I 2 称为转移电流比。 图 12-1

二、网络函数的计算方法 输出相量 H(jo)= 输入相量 正弦稳态电路的网络函数是以仙为变量的两个多项式 之比,它取决于网络的结构和参数,与输入的量值无关。 在已知网络相量模型的条件下,计算网络函数的基本 方法是外加电源法:在输入端外加一个电压源或电流源, 用正弦稳态分析的任一种方法求输出相量的表达式,然后 将输出相量与输入相量相比,求得相应的网络函数。对于 二端元件组成的阻抗串并联网络,也可用阻抗串并联公式 计算驱动,点阻抗和导纳,用分压、分流公式计算转移函数
二、网络函数的计算方法 输入相量 输出相量 H(j) 正弦稳态电路的网络函数是以ω为变量的两个多项式 之比,它取决于网络的结构和参数,与输入的量值无关。 在已知网络相量模型的条件下,计算网络函数的基本 方法是外加电源法:在输入端外加一个电压源或电流源, 用正弦稳态分析的任一种方法求输出相量的表达式,然后 将输出相量与输入相量相比,求得相应的网络函数。对于 二端元件组成的阻抗串并联网络,也可用阻抗串并联公式 计算驱动点阻抗和导纳,用分压、分流公式计算转移函数
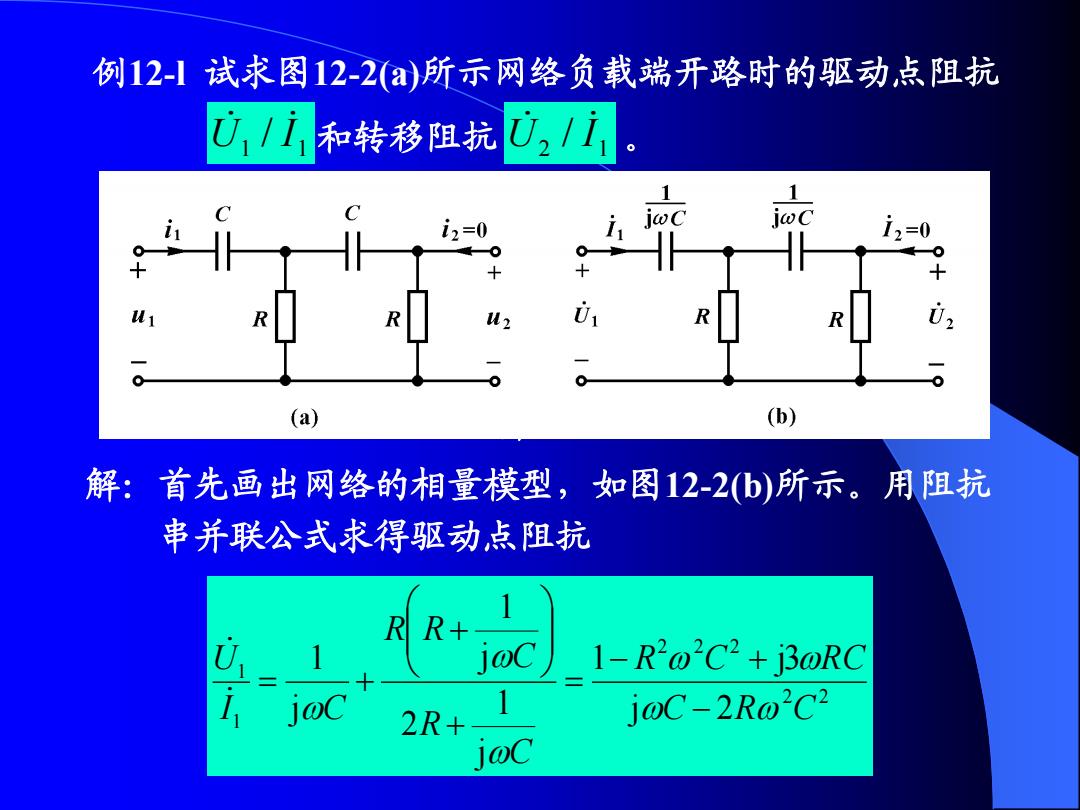
例12-】试求图12-2(a)所示网络负载端开路时的驱动点阻抗 U,/i和转移阻抗U1i jwc I2=0 (a) (b) 解:首先画出网络的相量模型,如图12-2b)所示。用阻抗 串并联公式求得驱动,点阻抗 RR+ U joC 1-R2@2C2+j3@RC 2R+ j@C-2R@2C2 joC
例12-l 试求图12-2(a)所示网络负载端开路时的驱动点阻抗 U 1 / I 1 和转移阻抗 U 2 / I 1 。 图 12-2 解:首先画出网络的相量模型,如图12-2(b)所示。用阻抗 串并联公式求得驱动点阻抗 2 2 2 2 2 1 1 j 2 1 j3 j 1 2 j 1 j 1 C R C R C R C C R C R R I C U
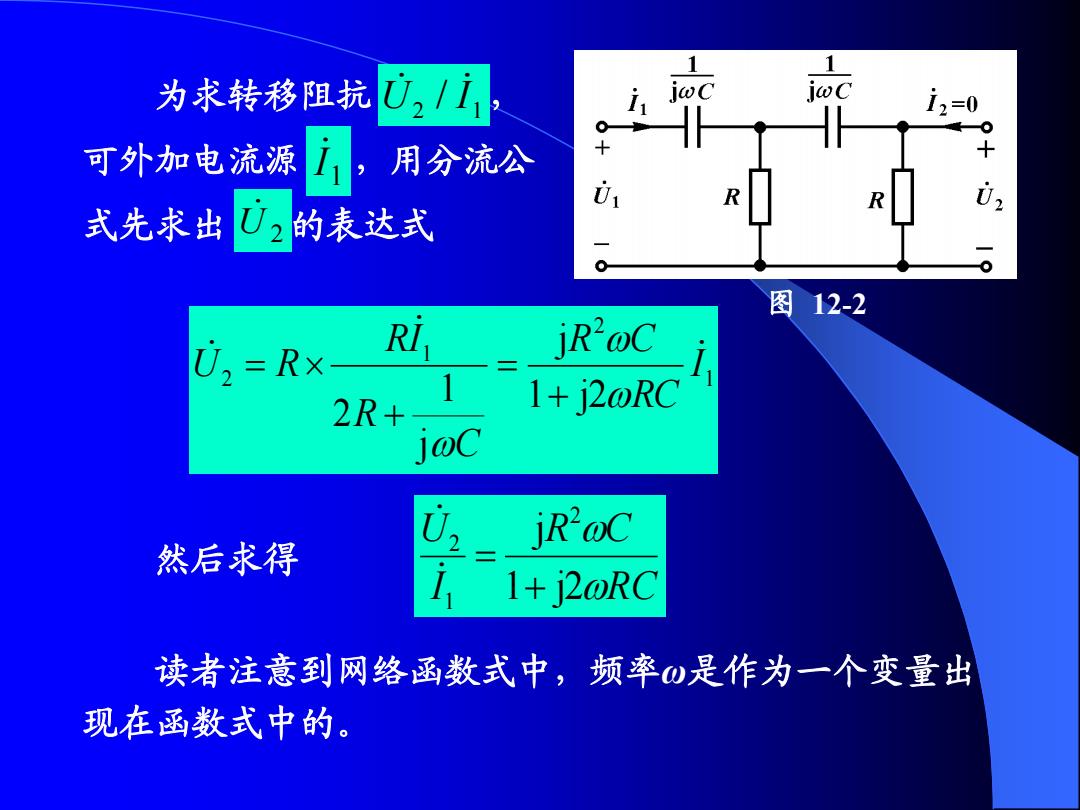
为求转移阻抗U2/i; i jwc 2=0 ,用分流公 。 可外加电流源 U2的表达式 01 R 式先求出 图12-2 U=R× RI jR-@C 2R+ 1 1+j2@RC jwC jR'@C 然后求得 U2= 读者注意到网络函数式中,频率ω是作为一个变量出 现在函数式中的
1 2 1 2 1 j2 j j 1 2 I RC R C C R RI U R 然后求得 RC R C I U 1 j2 j 2 1 2 读者注意到网络函数式中,频率ω是作为一个变量出 现在函数式中的。 为求转移阻抗 , 可外加电流源 ,用分流公 式先求出 U 2 的表达式 1 I 2 1 U / I 图 12-2
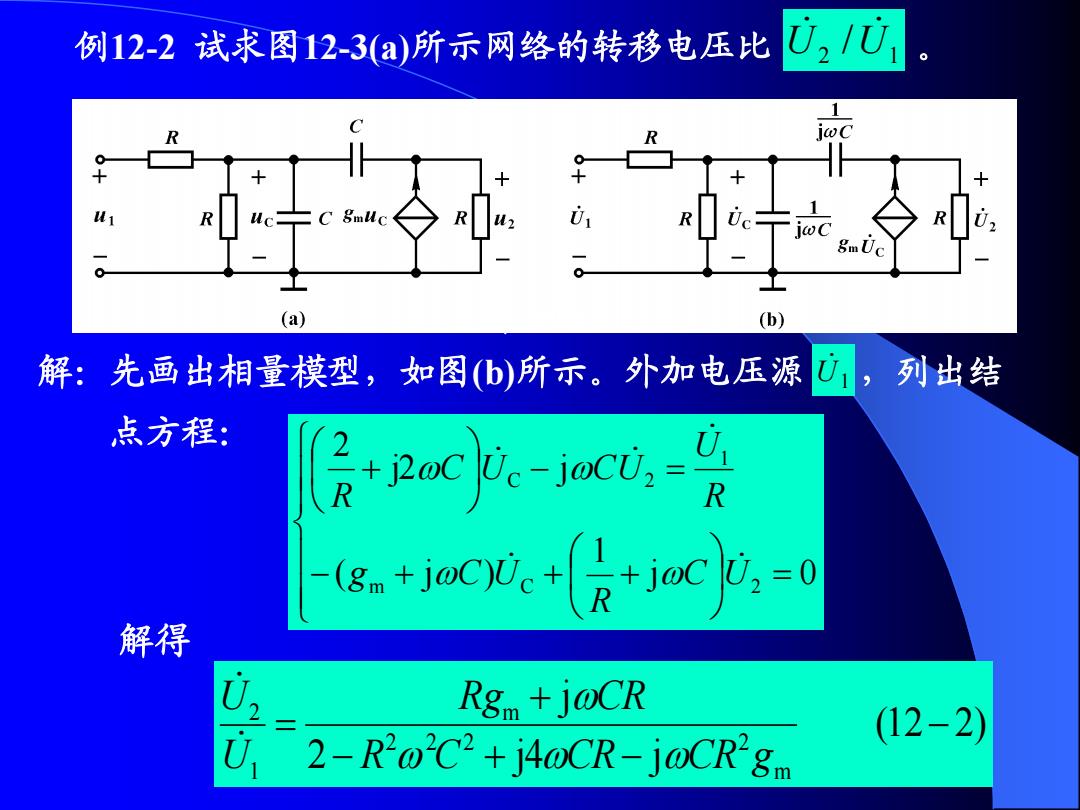
例12-2试求图12-3(a)所示网络的转移电压比 ☑21U个 C8muc gmUc (a) (b) 解:先画出相量模型,如图b)所示。外加电压源 U1,列出结 点方程: 食Rxc.-at-月 -s.+o心.+及+joc4,=0 解得 Rgm+j@CR (12-2) 2-R2@'C2+j4@CR-j@CR8m
解:先画出相量模型,如图(b)所示。外加电压源 ,列出结 点方程: U1 j 0 1 ( j ) j2 j 2 m C 2 1 C 2 C U R g C U R U C U CU R 解得 (12 2) 2 j4 j j m 2 2 2 2 m 1 2 R C CR CR g R g CR U U 例12-2 试求图12-3(a)所示网络的转移电压比 U 2 /U 1 。 图 12-3

三、网络函数与正弦波 网络函数H(Go)是输出相量与输入相量之比,HG0反 映输出正弦波振幅及相位与输入正弦波振幅及相位间的关 系。在已知网络函数的条件下,给定任一频率的输入正弦 波,即可直接求得输出正弦波。例如已知某电路的转移电 压比 HGo=+HGjo)1∠0o (12-3) 其中 12-4) θ(o)=Ψ2-1 (12-5)
(j ) | (j ) | ( ) (12 3) 1 2 H U U H 其中 ( ) (12 5) (j ) (12 4) 2 1 1 2 U U H 三、网络函数与正弦波 网络函数H(j)是输出相量与输入相量之比,H(j)反 映输出正弦波振幅及相位与输入正弦波振幅及相位间的关 系。在已知网络函数的条件下,给定任一频率的输入正弦 波,即可直接求得输出正弦波。例如已知某电路的转移电 压比

式(12-4)表明输出电压u2()的幅度为输入电压u1()幅 度的HGo倍,即 U2H(Ujo)川U1 式(12-5)表明输出电压u,()的相位比输入电压41()的 相位超前o,即 Ψ2=41+0(⊙) 若已知4,()=U1mc0s(ot4),则由41()引起的响应为 u,(t)=H(jo)Uim cos[ot+w+e(@)] (12-6) 对于其它网络函数,也可得到类似的结果
式(12-4)表明输出电压u2 (t)的幅度为输入电压u1 (t)幅 度的|H(j)|倍,即 2 1 U | H( j) |U 式(12-5)表明输出电压u2 (t)的相位比输入电压u1 (t)的 相位超前(),即 ( ) 2 1 若已知u1 (t)=U1mcos(t+1 ),则由u1 (t)引起的响应为 ( ) | (j ) | cos[ ( )] (12 6) u2 t H U1m t 1 对于其它网络函数,也可得到类似的结果
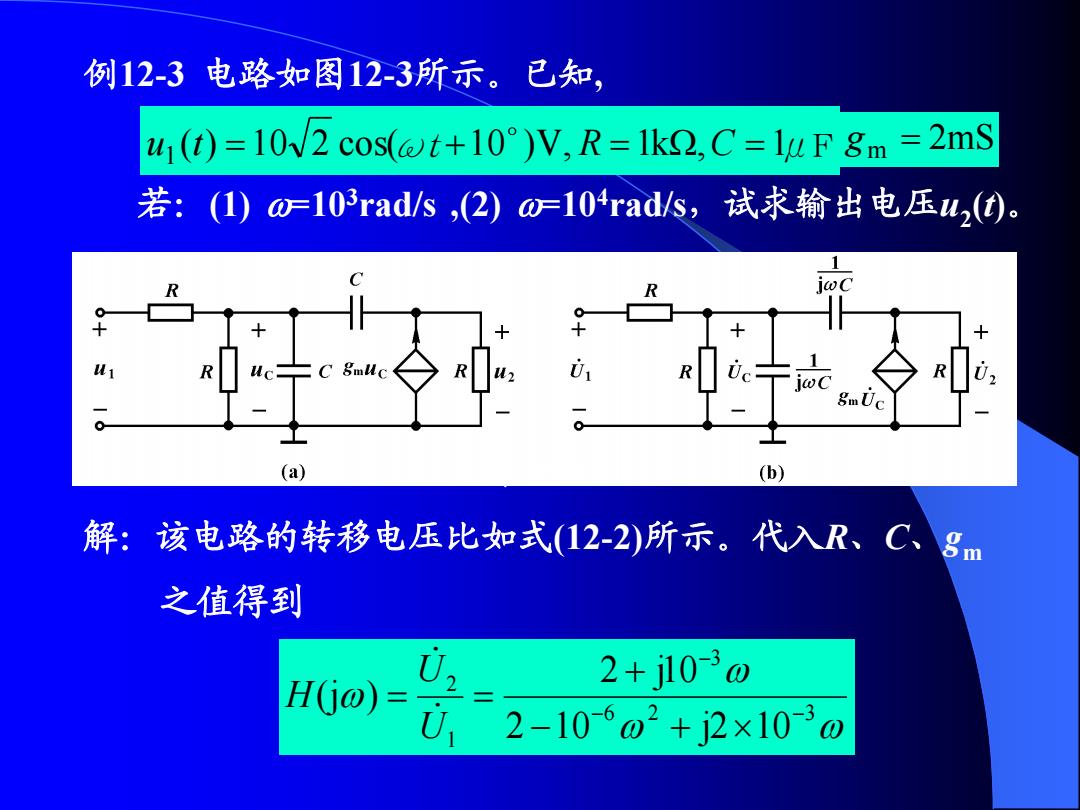
例12-3 电路如图12-3所示。已知, u(t)=10v2 cos(@t+10)V,R=1k,C=luF gm =2mS 若:(1)o103rad/s,(2)o-104rads,试求输出电压42(). o c 8mUc (a) (b) 解:该电路的转移电压比如式(12-2)所示。代入R、C、gm 之值得到 U2 H(j0) 2+j10-3o 02-106o2+j2×1030
例12-3 电路如图12-3所示。已知, 若:(1) =103rad/s ,(2) =104rad/s,试求输出电压u2 (t)。 u1 (t) 1 0 2 cos(ωt 1 0 )V, R 1k,C 1μF g m 2mS 6 2 3 3 1 2 2 10 j2 10 2 j10 ( j ) U U H 解:该电路的转移电压比如式(12-2)所示。代入R、C、gm 之值得到 图 12-3