中国地质大学（武汉）：《数字信号处理 Digital Signal Processing》课程教学资源（试卷习题）各章习题讲解（1/2）

第一章习题讲解

第一章习题讲解

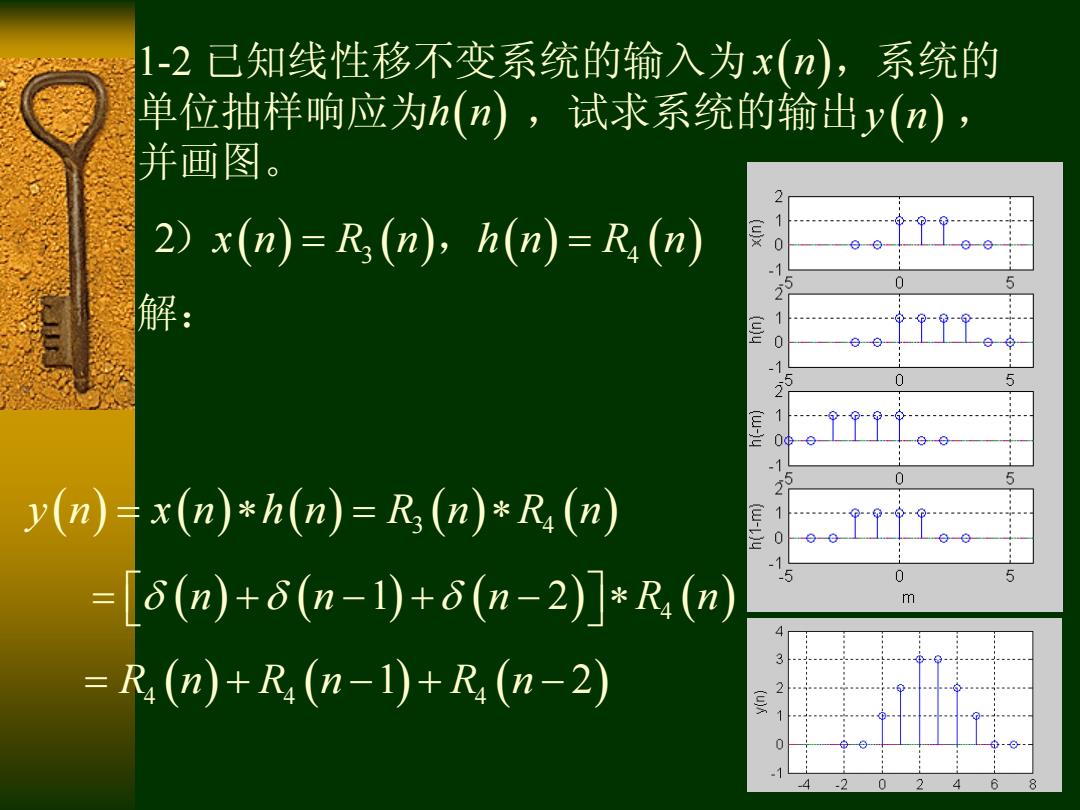
1-2已知线性移不变系统的输入为x(n),系统的 单位抽样响应为h(n,试求系统的输出y(n), 并画图。 2 2)x(n）=R(n),h(nm)=R,(n) 0 5 解： 2 1 0 -1 2 5 (w-jy 1 -1 0 5 y(n)=x(n)*h(n)=R(n)*R,(n) 0 =[8(n)+8(n-1)+δ(n-2)]*R(n) m =R(n)+R(n-1)+R(n-2) 2

解： 2） ， x n R n h n R n     3 4                 3 4 y n x n h n R n R n     1-2 已知线性移不变系统的输入为 ，系统的 单位抽样响应为 ，试求系统的输出 ， 并画图。 x n  h n  y n          4            n n n R n 1 2        R n R n R n 4 4 4    1 2   

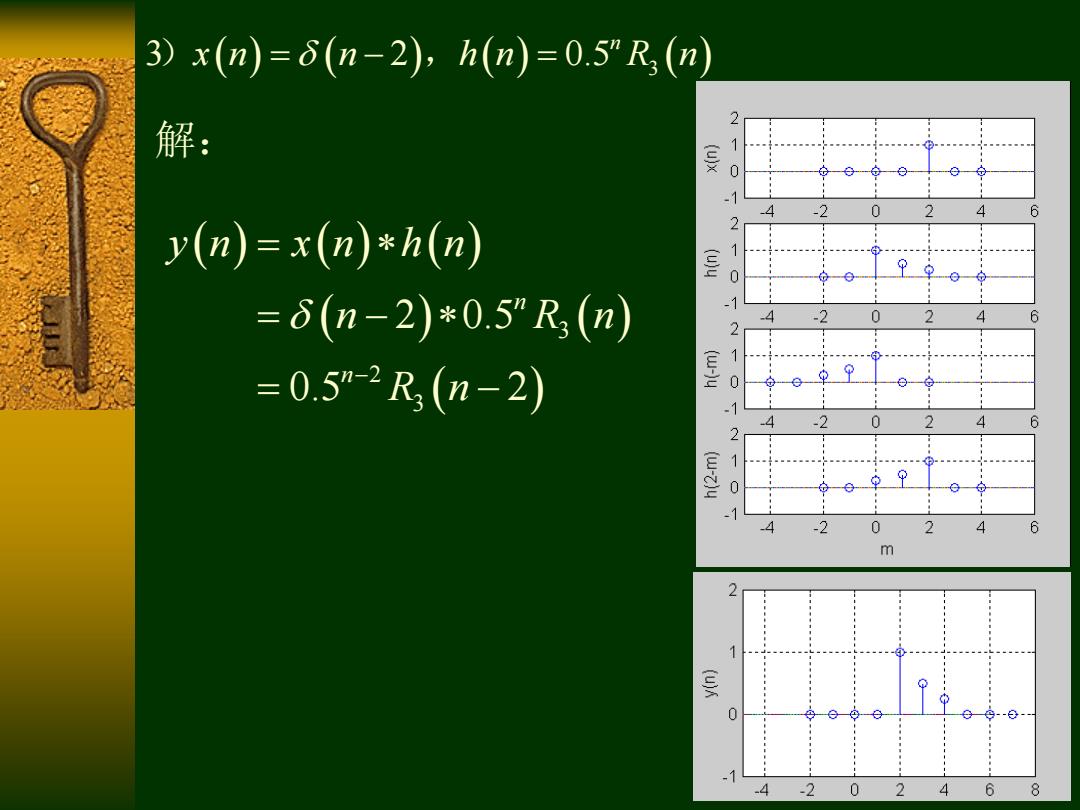
3)x(n)=(n-2),h(n）=0.5”R(n) 解： 2 吴 101 4 2 0 6 y(n)=x(n)*h(n) 2 10 =(n-2)*0.5”R(n） 1 0 2 6 1 =0.5”-2R(n-2) (w)y 0 1 .2 0 A 6 2 E-3= 10 1 -2 0 2 6 m .4 -2 0 2 4 6 8

解： 3 2 0.5       3   n ） ， x n n h n R n                 3 2 3 2 0.5 0.5 2 n n y n x n h n n R n R n         

4)x(nm)=2”(-n-),h(n）=0.5(n) 解：y(m)=∑x(mh(n-m) 0 m=-00 当n≤-1时 1 0.5 0 y(n)=Σ2”0.5m 5 1 E 50 0 5 1 =2∑4 5 0 m=-o0 1 0 n=-1 =2"∑4m 0 5 0 1 m=-n n<-1 0 4” 4 5 0 5 =2-n 2" m 1-4 3

解：       m y n x m h n m      4 2 1 0.5         n n ） ， x n u n h n u n     当 时 n  1   2 0.5 n m n m m y n      2 4 n n m m     2 4 n m m n        1 4 4 2 2 1 4 3 n n n     

当n≥0时 1 复 0 0 5 y(m)=∑2”.0.5m 1 S 0 5 5 0 m=-00 (w-)y 1 5 -2∑4 0 5 (w-u)y n=.1 1=-00 50 P 5 0 5 1 n>.1 =24 50 m 0.8 6 y=2-m-1)+52) 0 -01 -5 0 5

当 时 n  0   1 2 0.5 m n m m y n             4 1 2 1 2 3 3 n n y n u n u n         1 2 4 n m m      1 2 4 n m m       1 1 4 1 2 2 1 4 3 n n        

1-3已知h(n)=a"u(-n-1),0<a<1,通过直 接计算卷积和的办法，试确定单位抽样响 应为h(n)的线性移不变系统的阶跃响应

   1 0 1  n h n a u n a       ， h n  1-3 已知 ，通过直 接计算卷积和的办法，试确定单位抽样响 应为 的线性移不变系统的阶跃响应

解：LSI系统的阶跃响应是指输入为阶跃序列时 系统的输出，即 x(n)=u(n),h(n）=a"u(-n-I),0.1 m=n+] 0 -10 0 5 10 m

解：LSI系统的阶跃响应是指输入为阶跃序列时 系统的输出，即    1 ,0 1  n h n a u n a  x n u n     ,                m y n x n h n x m h n m   求      当 时 n  1 当 时 n  0     0 n m m y n a       1 n a a        1 n m m n y n a        1 a a  

1 .5 中 0 10 5 0 5 10 1 吴 0 5 10 5 5 10 50 5 0 5 10 (E,s× -150 n.1 0 .10 0 5 10 m 5 3 2 ② 5

   1   1 1 n a a y n u n u n a a        

-4判断下列每个序列是否是周期性的，若是周期 性的，试确定其周期 解：为正弦序列其中0，= 3π 2π14 是有理数 3 00 N=14是满足x(n+N)=x(n)的最小正整数 ∴x(n)为周期序列，周期为14

1-4 判断下列每个序列是否是周期性的，若是周期 性的，试确定其周期   3 1 cos 7 8 x n A n           （ ） 0 3 7  其中  0 2 14 3    是有理数 解： 为正弦序列 x n( ) x n 为周期序列，周期为14 N x n N x n    14 ( ) ( ) 是满足 的最小正整数

1-6试判断y(n)=[x(n)]是否是线性系统？ 并判断是否是移不变系统？ 解：设T[x(n=[x(n)T[x(n=[x(n :T[x(n）+x,(n)]=[x(n)+x(n)] =[x(n)了+[x,(m)]+2x(n)x,(n) ≠T[x(n)]+T[x,(n)]不满足可加性 或T[ax(n)]-[ax(m)了=a[x(n)]≠ar[x(n)] 不满足比例性 .不是线性系统 :T[x(n-m)]=[x(n-m)]=y(n-m)=[x(n-m] 是移不变系统

1-6 试判断 是否是线性系统？ 并判断是否是移不变系统？     2 y n x n              2 T x n x n x n x n     1 2 1 2        不满足可加性 或     2 T ax n ax n          不满足比例性  不是线性系统     2 T x n m x n m             是移不变系统         2 2        x n x n x n x n 1 2 1 2 2       T x n T x n     1 2         解：设     2 1 1 T x n x n ( ) ( )      2 2 2 T x n x n ( ) ( )      2 2   a x n aT x n             2  y n m x n m    ( )