中国地质大学（武汉）：《数字信号处理 Digital Signal Processing》课程教学资源（课件讲稿）第二章 z变换

第二章z变换 ◆时域分析方法 ◆变换域分析方法： 连续时间信号与系统 Laplace变换 Fourier变换 离散时间信号与系统 z变换 Fourier变换

第二章 z变换 时域分析方法 变换域分析方法： 连续时间信号与系统 Laplace变换 Fourier变换 离散时间信号与系统 z变换 Fourier变换

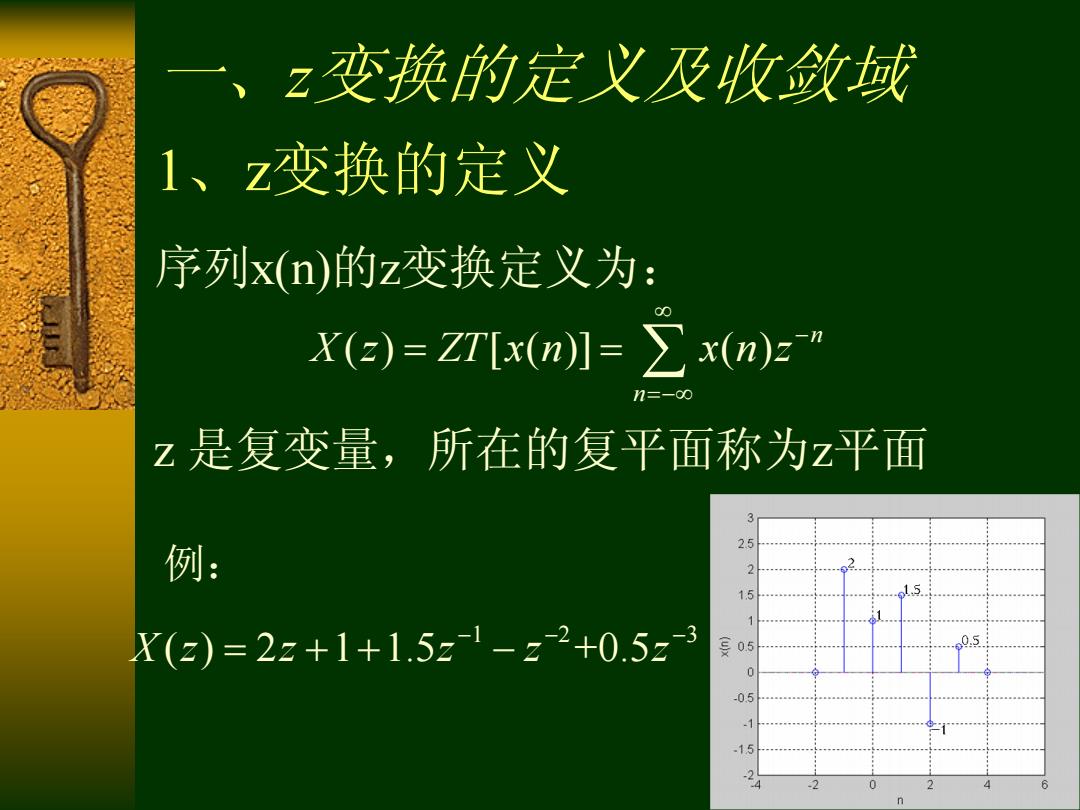
一、z变换的定义及收敛域 1、z变换的定义 序列x(n)的z变换定义为： X(e)=ZT[x(n】=∑x(n)z” n=-o0 Z是复变量，所在的复平面称为z平面 3 例： 25 2 15 X(z)=2z+1+1.5z1-z2+0.5z-3 号05 .5 05

一、z变换的定义及收敛域 1、z变换的定义 序列x(n)的z变换定义为： ( ) [ ( )] ( ) n n X z ZT x n x n z       z 是复变量，所在的复平面称为z平面 例： 1 2 3 X z z z z z ( ) 2 1 1.5 +0.5       

2、z变换的收敛域与零极点 ◆对于任意给定序列x(n),使其z变换X(z) 收敛的所有z值的集合称为X(z)的收敛域 级数收敛的充要条件是满足绝对可和 ∑x(n)z=M<∞ n=-o0 令X(a)= P() 2() 则X(z)的零点：使X(z=O的点 即P(z)=0和当Q(z)阶次高于P(z)时Q(z)→∞ X(Z)的极点：使X(z)→∞的点， 即Q(z)=0和当P(z)阶次高于Q(z)时P(z)→o

2、z变换的收敛域与零极点 对于任意给定序列x(n)，使其z变换X(z) 收敛的所有z值的集合称为X(z)的收敛域。 级数收敛的充要条件是满足绝对可和 ( ) n n x n z M        ( ) ( ) ( ) P z X z Q z 令  X(z) X(z)=0 P z Q z P z Q z ( ) 0 ( ) ( ) ( )    则 的零点：使 的点， 即 和当 阶次高于 时 X(z) X(z) Q z P z Q z P z ( ) 0 ( ) ( ) ( )      的极点：使 的点， 即 和当 阶次高于 时

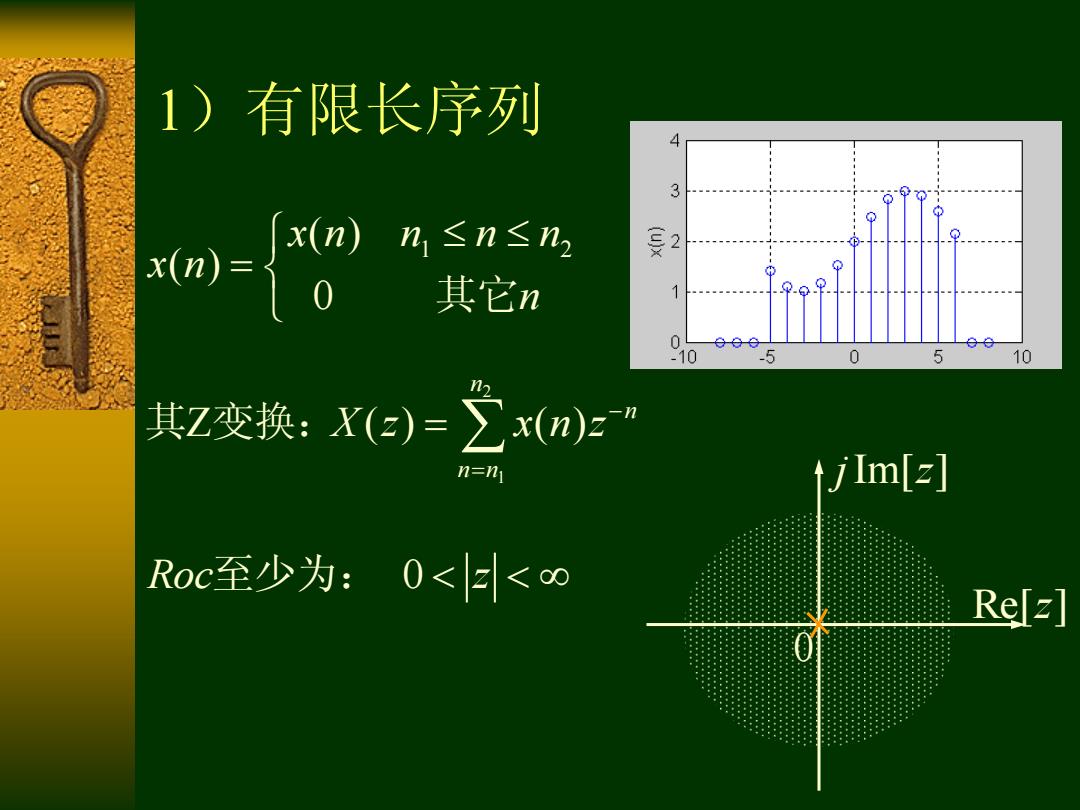
1)有限长序列 3 x(n)n,≤n≤n2 2 其它n 1 0 -10 0 5 10 其Z变换：X(e)=∑x(n)z” n=n tjlm[z] Roc至少为：0<<∞ Refz]

1）有限长序列 1 2 ( ) ( ) 0 x n n n n x n n       其它 2 1 Z ( ) ( ) n n n n X z x n z  其 变换：   Roc z 至少为： 0    Re[ ]z j z Im[ ] 0

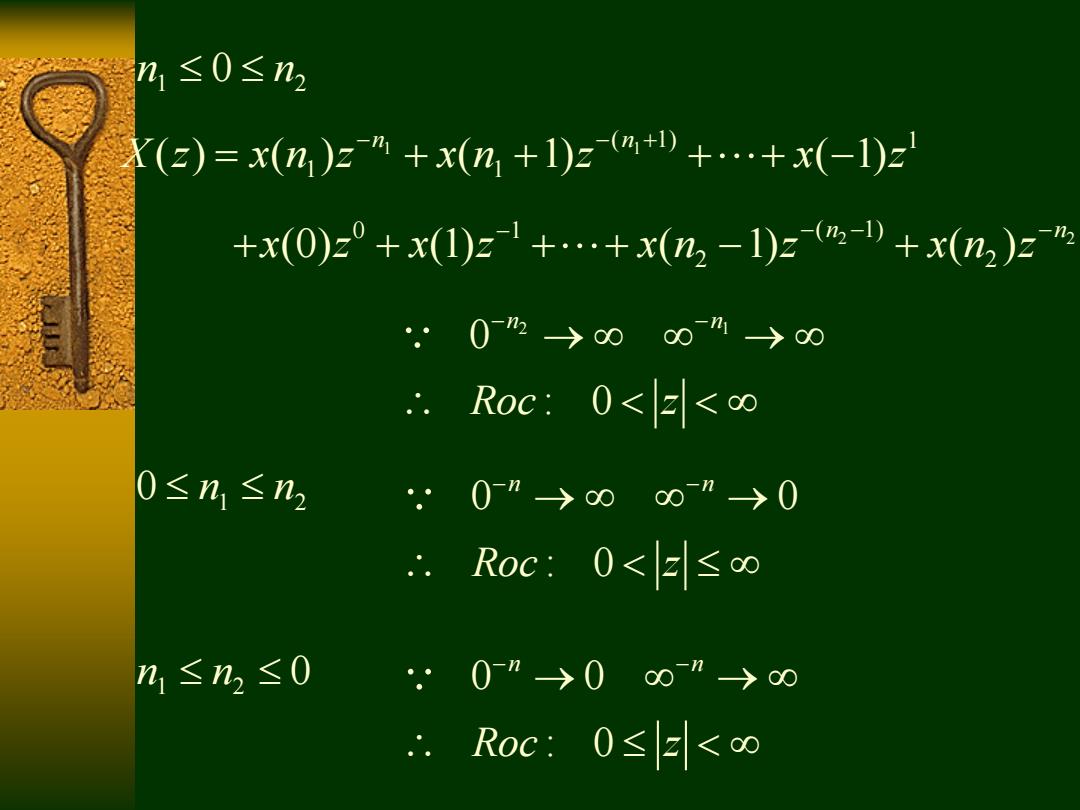
h1≤0≤n2 (a)=x(n)zm+x(n,+1)za+…+x(-1)z +x(0)z°+x(1)z+…+x(n2-1)z,-D+x(n2)z% .0m→0000%>00 Roc:0<E<∞ 0≤n,≤n2 .0-”→00”→0 Roc:0<E≤∞ n1≤n2≤0 .0-”→000”-→00 Roc:0≤E<∞

n n 1 2   0 1 1 ( 1) 1 1 1 ( ) ( ) ( 1) ( 1) n n X z x n z x n z x z         2 2 0 1 ( 1) 2 2 (0) (1) ( 1) ( ) n n x z x z x n z x n z           2 1 0 : 0 n n Roc z            0   n n 1 2 0 0 : 0 n n Roc z           0 0 : 0 n n Roc z           n n 1 2   0

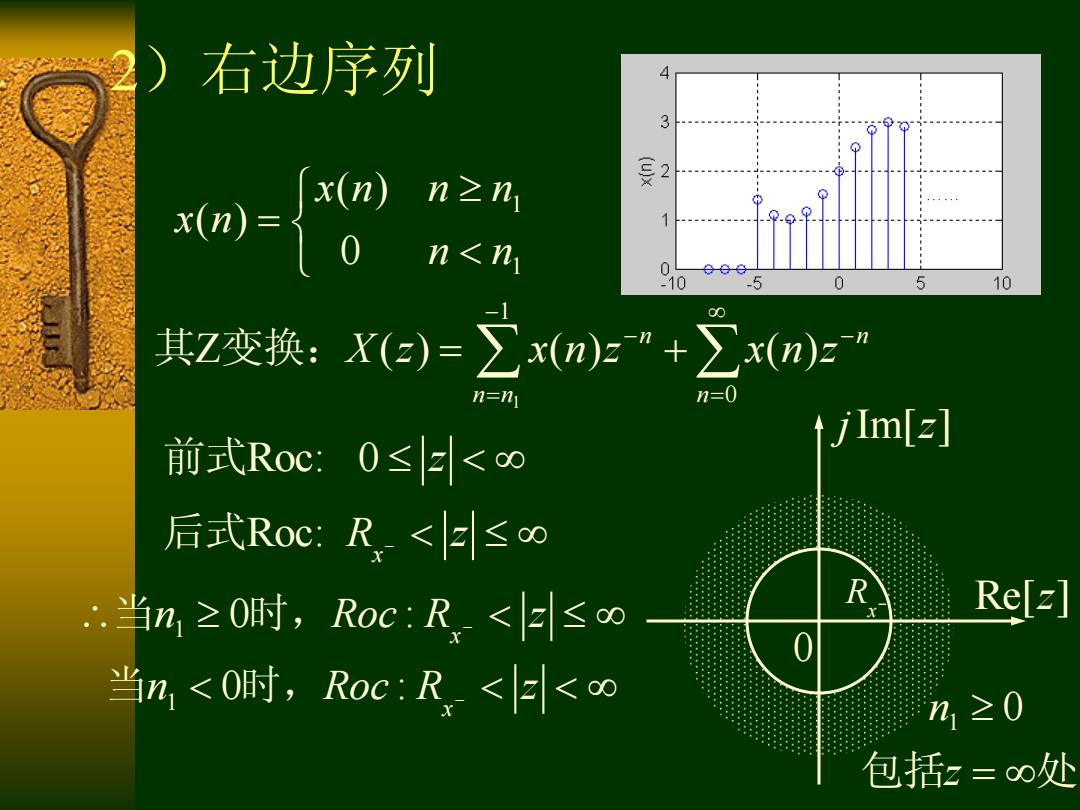
右边序列 4 3 x(n)n≥n 2 x(n) 1 ② n<n 0 10 -5 0 5 10 其Z变换：X(e)=∑x(n)z”+∑x(n)z” n=n n=0 前式Roc:0≤E<∞ tjlm[=] 后式RoCR,<E≤w R .当n,≥0时，Roc:R,<E≤o Re[z] 当h1<0时，Roc:R,<E<oo n,≥0 包括z=∞处

2）右边序列 1 1 ( ) ( ) 0 x n n n x n n n       1 1 0 Z ( ) ( ) ( ) n n n n n X z x n z x n z       其 变换：     前式Roc: 0    z Roc: x 后式 R z     1 1 0 : 0 : x x n Roc R z n Roc R z            当 时， 当 时， Re[ ]z j z Im[ ] 0 x R  包括 处 z   1 n  0

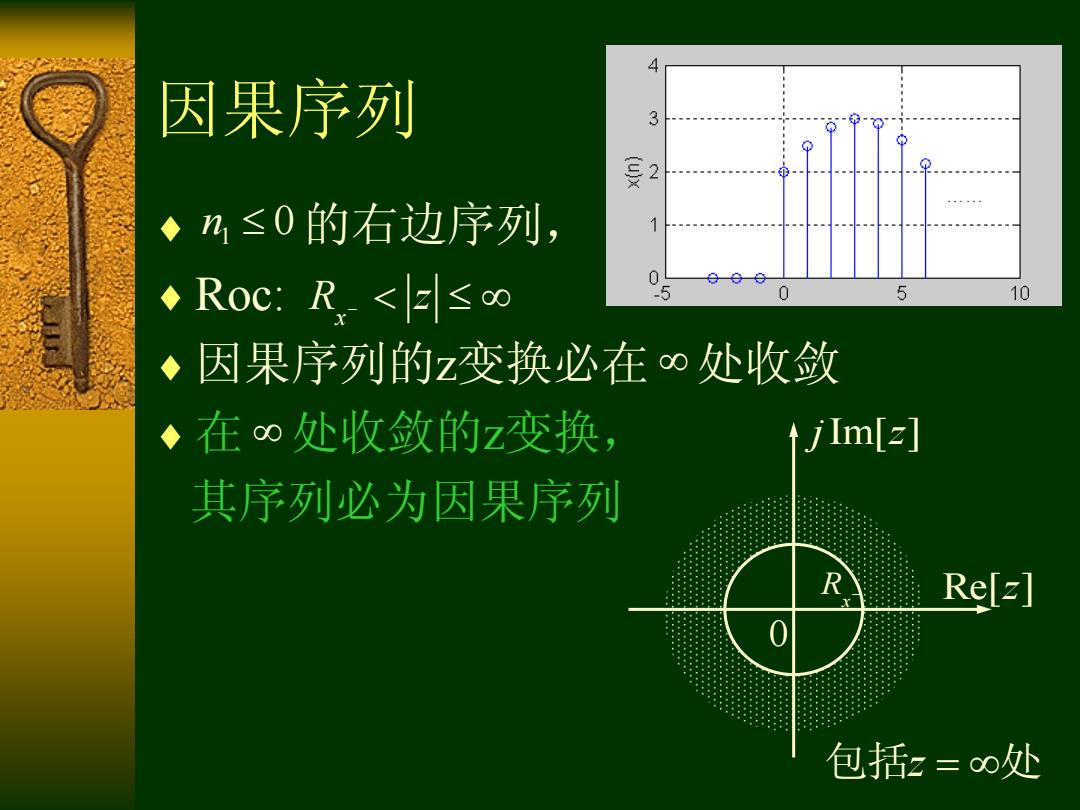
A 因果序列 3 2 ◆n≤0的右边序列， 1 0 ◆RoC:R,<E≤o 5 10 ◆因果序列的z变换必在∞处收敛 ◆在∞处收敛的z变换， jIm[z] 其序列必为因果序列 Re[=] 包括z=∞处

因果序列  的右边序列，  Roc: 因果序列的z变换必在 处收敛 在 处收敛的z变换， 其序列必为因果序列 n1  0 x R z       Re[ ]z j z Im[ ] 0 x R  包括 处 z  

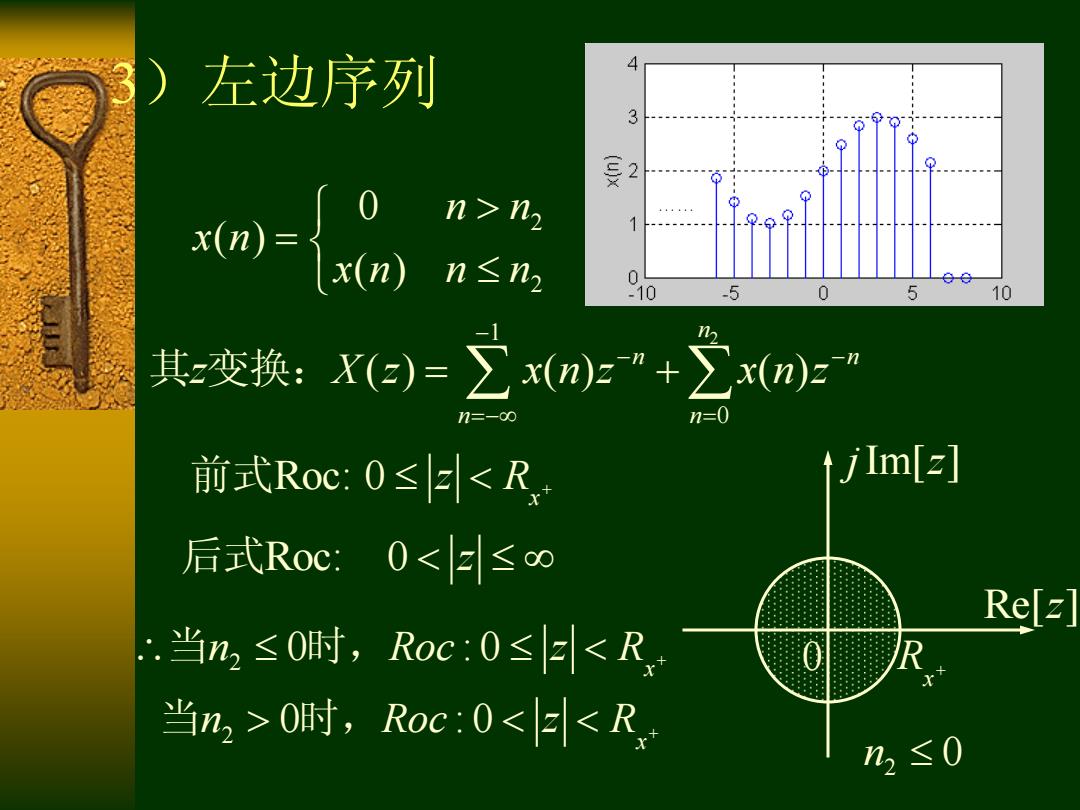
)左边序列 4 3 2 ) n> -10 -5 0 5 10 其-变换：X(e)=∑xn)”+∑xm)z” n=-o∞ n=0 前式Roc:0≤E0时，Roc:0<<R h≤0

3）左边序列 2 2 0 ( ) ( ) n n x n x n n n       1 2 0 ( ) ( ) ( ) n n n n n z X z x n z x n z      其 变换：     Roc: 0 x 前式   z R  后式 Roc: 0    z 2 2 0 : 0 0 : 0 x x n Roc z R n Roc z R          当 时， 当 时， Re[ ]z j z Im[ ] 0 x R  n2  0

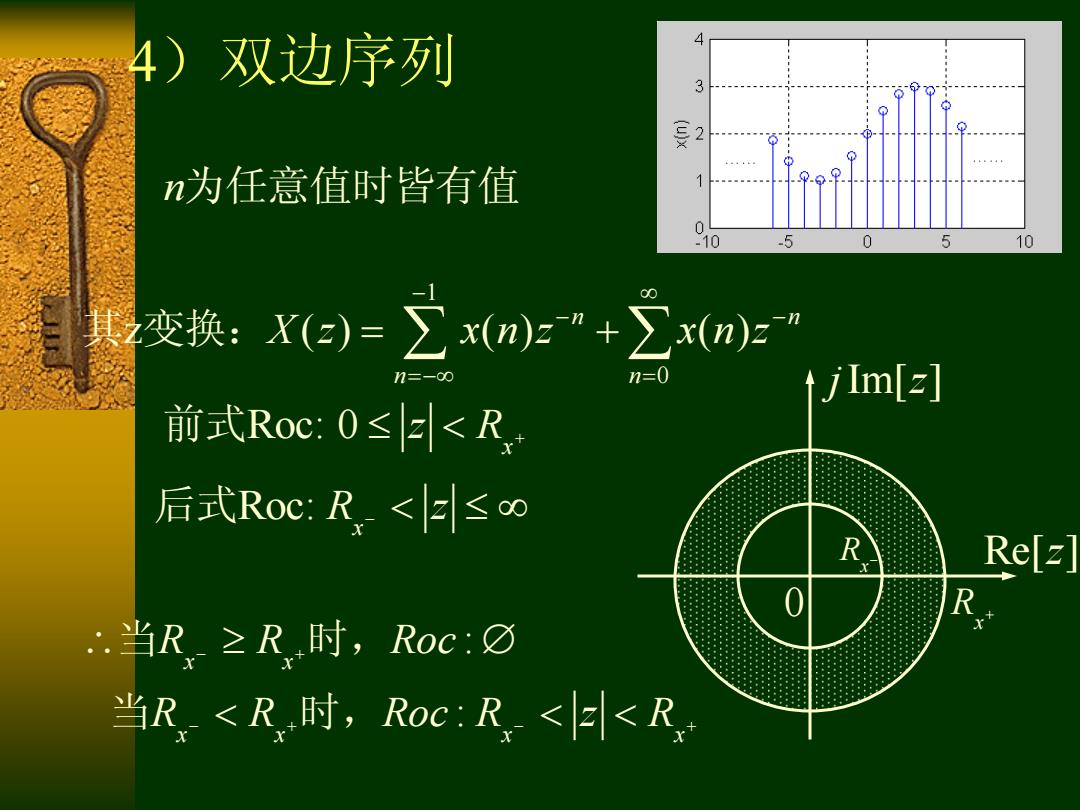
4)双边序列 4 3 2 n为任意值时皆有值 1 10 0 5 10 其 变换：Xa)=∑m)”+∑xnz 11=-00 =0 tjlm[=] 前式Roc:0≤E<R, 后式RoC:R,<≤∞ R Re[z] .当R≥R时，Roc:O 当R<R,时，Roc:R<E<R

4）双边序列 n为任意值时皆有值 1 0 z ( ) ( ) ( ) n n n n X z x n z x n z       其 变换：     Roc: 0 x 前式   z R  Roc: x 后式 R z    : : x x x x x x R R Roc R R Roc R z R             当 时， 当 时， Re[ ]z j z Im[ ] 0 x R  x R 

例求x(n)=Rv(n)的z变换及其收敛域 00 解：X(z∑x(n)"=∑Rv(m)z n=-o∞ n=-o∞ 2- n=n 1-9 h=0 -1-z习 n,→o时须满足9<1 2W-1 z-(z-1) tjlm[z] 2π1 零点：三=eNr=1N-1 Refz] 极点：z=0(N-1)阶 Roc:0<z≤o

1 ( ) ( ) z N 例：求 的 变换及其收敛域 x n R n  Re[ ]z j z Im[ ] 0 X(z)= ( ) = ( ) n n N n n x n z R n z       解：   1 0 = N n n z     2 1,..., 1 r j N z e r N  零点：    极点： （ ）阶 z N   0 1 Roc z : 0    2 1 2 1 1 1 n n n n n n q q q q       1 1 1 N z z      2 n q    时须满足 1 1 1 ( 1) N N z z z    