
第五章数字滤波器的基本结构
第五章 数字滤波器的基本结构

一、数字滤波器结构的表示方法 数字滤波器的系统函数: H(a)= Y() b k=0 X(a) 1-∑az 常系数线性差分方程: 00=∑a0-)+2A,n-) k=0
一、数字滤波器结构的表示方法 数字滤波器的系统函数: 0 1 ( ) ( ) ( ) 1 M k k k N k k k b z Y z H z X z a z 1 0 ( ) ( ) ( ) N M k k k k y n a y n k b x n k 常系数线性差分方程:

M切-立aa-k+立Axn-) k-0 基本运算单元 方框图 流图 单位延时 常数乘法器 加法器
a a 1 z 1 z 1 0 ( ) ( ) ( ) N M k k k k y n a y n k b x n k 加法器 常数乘法器 单位延时 基本运算单元 方框图 流图
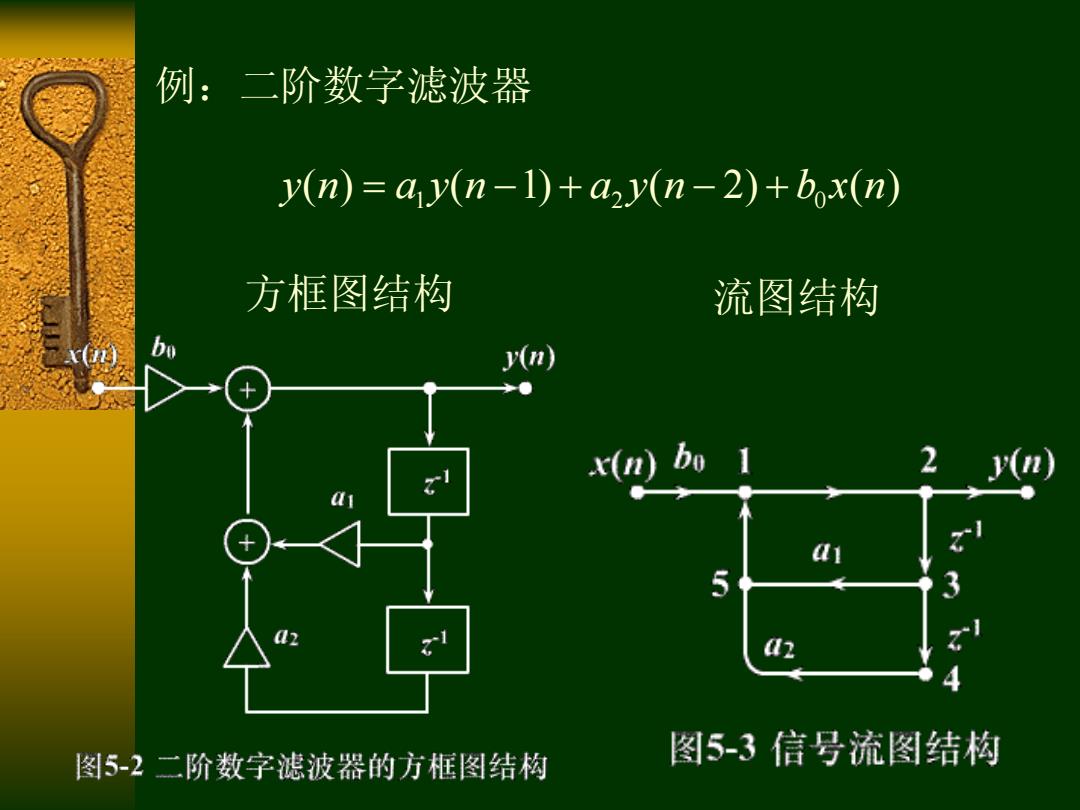
例:二阶数字滤波器 y(m)=ay(n-1)+a2y(n-2)+bx(n) 方框图结构 流图结构 y(n) x(u)bo 1 5 图5-2二阶数字滤波器的方框图结构 图5-3信号流图结构
例:二阶数字滤波器 1 2 0 y n a y n a y n b x n ( ) ( 1) ( 2) ( ) 方框图结构 流图结构
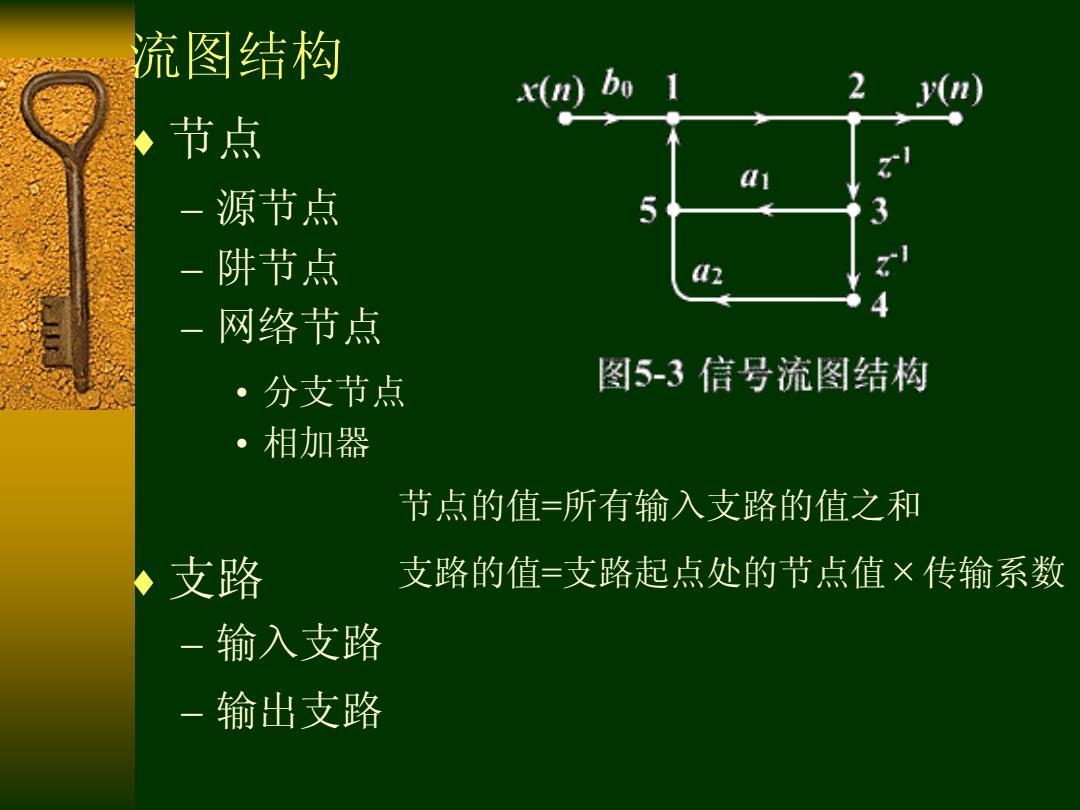
流图结构 x(m)bo 1 节点 -源节点 5 阱节点 网络节点 ·分支节点 图5-3信号流图结构 ·相加器 节点的值=所有输入支路的值之和 ◆支路 支路的值=支路起点处的节点值×传输系数 -输入支路 -输出支路
流图结构 节点 – 源节点 支路 – 阱节点 – 网络节点 • 分支节点 – 输入支路 • 相加器 节点的值=所有输入支路的值之和 – 输出支路 支路的值=支路起点处的节点值 传输系数

二、R数字滤波器的基本结构 R数字滤波器的特点: 系统函数:H()= Y() k=0 X() 1-∑az4 k=1 差分方程:m)=之n-)+之,xn-) k=1 1)系统的单位抽样相应(m)无限长 2)系统函数H)在有限z平面(0<<∞)上有极点存在 3)存在输出到输入的反馈,递归型结构
二、IIR数字滤波器的基本结构 1)系统的单位抽样相应h(n)无限长 IIR数字滤波器的特点: 3)存在输出到输入的反馈,递归型结构 2)系统函数H(z)在有限z平面( 0 z )上有极点存在 0 1 ( ) ( ) ( ) 1 M k k k N k k k b z Y z H z X z a z 系统函数: 1 0 ( ) ( ) ( ) N M k k k k y n a y n k b x n k 差分方程:

◆R数字滤波器的基本结构: 直接I型 -直接Ⅱ型(典范型) 级联型 并联型
IIR数字滤波器的基本结构: – 直接Ⅰ型 – 直接Ⅱ型(典范型) – 级联型 – 并联型

1、直接I型 差分方程:切-立a,n-k)+立40n-) k=0 x(n) bo y(n) x(n-1) br J-1) 需N+M个 b2 2 延时单元 x(n-2) y(1-2) x(n-M+1) ibM-1 AN-I Jy(-N+1) x(n-M) bM aN y(n-)
1、直接Ⅰ型 差分方程: 1 0 ( ) ( ) ( ) N M k k k k y n a y n k b x n k 需N+M个 延时单元
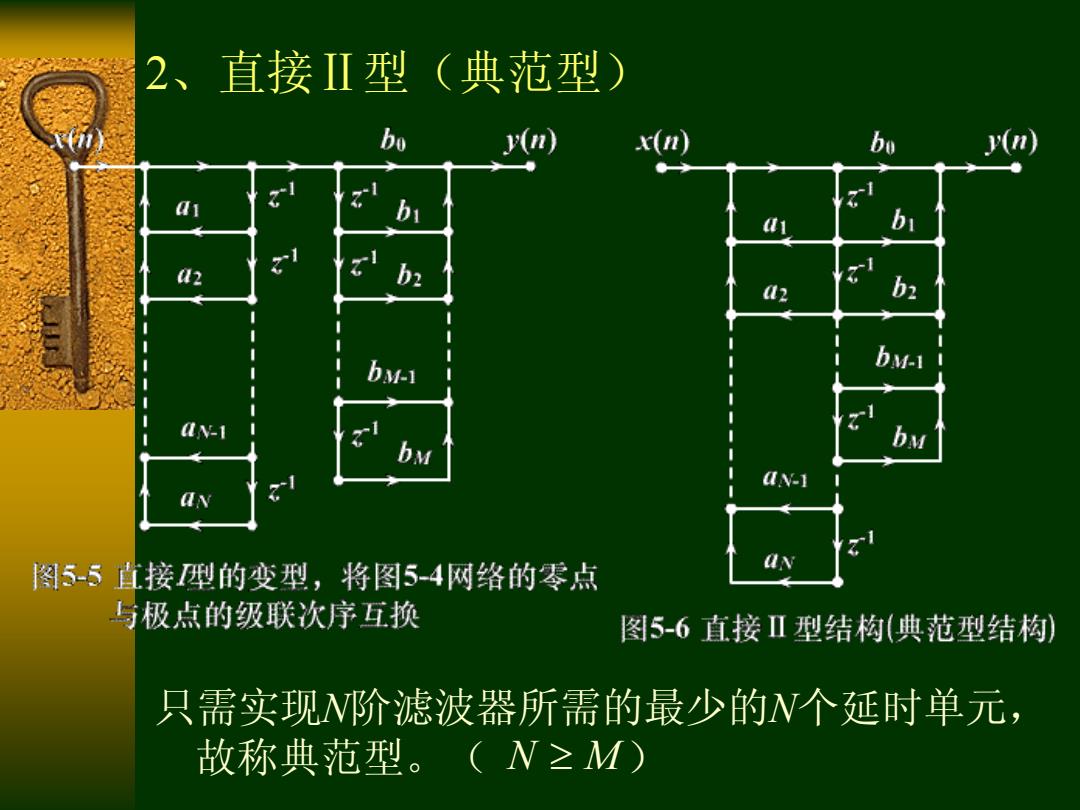
2、直接Ⅱ型(典范型) bo x(n) bo y(n) a 12 b bM-1 bM-i bM bM dN-1 aN 图5-5直接型的变型,将图5-4网络的零点 与极点的级联次序互换 图5-6直接Ⅱ型结构(典范型结构) 只需实现阶滤波器所需的最少的N个延时单元, 故称典范型。(N≥M)
2、直接Ⅱ型(典范型) N M 只需实现N阶滤波器所需的最少的N个延时单元, 故称典范型。( )

直接型的共同缺点: ◆系数4,b对滤波器的性能控制作用不明显 ◆极点对系数的变化过于灵敏,易出现不稳定或 较大误差 ◆运算的累积误差较大
直接型的共同缺点: k a k 系数 , b 对滤波器的性能控制作用不明显 极点对系数的变化过于灵敏,易出现不稳定或 较大误差 运算的累积误差较大