中国地质大学（武汉）：《数字信号处理 Digital Signal Processing》课程教学资源（课件讲稿）第四章 快速傅里叶变换 Fast Fourier Transform（FFT）

第四章快速傅里叶变换 FFT:Fast Fourier Transform 1965年，Cooley,Tukey 《机器计算傅里叶级数的一种算法》

第四章 快速傅里叶变换 FFT: Fast Fourier Transform 1965年，Cooley, Tukey 《机器计算傅里叶级数的一种算法》

一、直接计算DFT的问题及改进途径 N点有限长序列x(n) DFT: X()=DFT[x(m】-∑x(m)WRv(k) n=0 IDFT: Dr7T2g”Rw

一、直接计算DFT的问题及改进途径 1 0 : ( ) [ ( )] ( ) ( ) N nk N N n DFT X k DFT x n x n W R k      1 0 : 1 ( ) [ ( )] ( ) ( ) N nk N N k IDFT x n IDFT X k X k W R n N       N x n 点有限长序列 ( )

运算量 复数乘法 复数加法 一个X) N N-1 o时 N个XE) N2 N(N-1) n=0 (N点DFT) (a+jb)(c+jd)=(ac-bd)+j(ad+cb) 实数乘法 实数加法 一次复乘 4 2 一次复加 2 一个X() 4N 2N+2(N-1)=2(2N-1) N个X() 4N2 2N(2N-1) (N点DFT)

运算量 复数乘法 复数加法 一个X(k) N N – 1 N个X(k) (N点DFT) N 2 N (N – 1) 实数乘法 实数加法 一次复乘 4 2 一次复加 2 一个X (k) 4N 2N+2 (N – 1)=2 (2N – 1) N个X (k) (N点DFT) 4N 2 2N (2N – 1) 1 0 ( ) N nk N n x n W    a jb c jd ac bd j ad cb            

WW的特性， e 对称性（()'=W=W9-=-) W.W成W.W 周期性 WWNmAWN) 可约性W=WwW=W 2π 2πN mnk mN e=em=-1 特殊点：W=1W2=-1W+w2)=-W

nk WN 的特性 * ( ) ( ) ( ) nk nk N n k n N k W W W W N N N N    对称性    ( ) ( ) nk N n k n N k W W W N N N   周期性   nk mnk 可约性 W W N mN  / / nk nk m W W N N m  0 / 2 ( / 2) 1 1 N k N k W W W W N N N N  特殊点：      2 j nk nk N W e N    Nk nk W W N N    nN nk W W N N    2 j mnk mN e    2 2 1 N j N j e e         

FFT算法的基本思想： 利用DFT系数的特性，合并DFT运算中的某些项， 把长序列DFT→短序列DFT,从而减少其运算量。 FFT算法分类： 时间抽选法 DIT:Decimation-In-Time 频率抽选法 DIF:Decimation-In-Frequency

FFT算法分类:  时间抽选法 DIT: Decimation-In-Time  频率抽选法 DIF: Decimation-In-Frequency FFT DFT DFT DFT DFT  算法的基本思想： 利用 系数的特性，合并 运算中的某些项， 把长序列 短序列 ，从而减少其运算量

二、按时间抽选的基2FFT算法 1、算法原理 设序列点数N=2L,L为整数。 若不满足，则补零 N为2的整数幂的FFT算法称基-2FFT算法。 将序列x(n)按n的奇偶分成两组： x(2r)=x(r) r=0,1,.,N/2-1 x(2r+)=x(r)

二 、按时间抽选的基-2FFT算法 1、算法原理 设序列点数 N = 2L ，L 为整数。 若不满足，则补零         1 2 2 2 1 x r x r x r x r    r N   0,1,..., / 2 1 将序列x(n)按n的奇偶分成两组： N为2的整数幂的FFT算法称基-2FFT算法

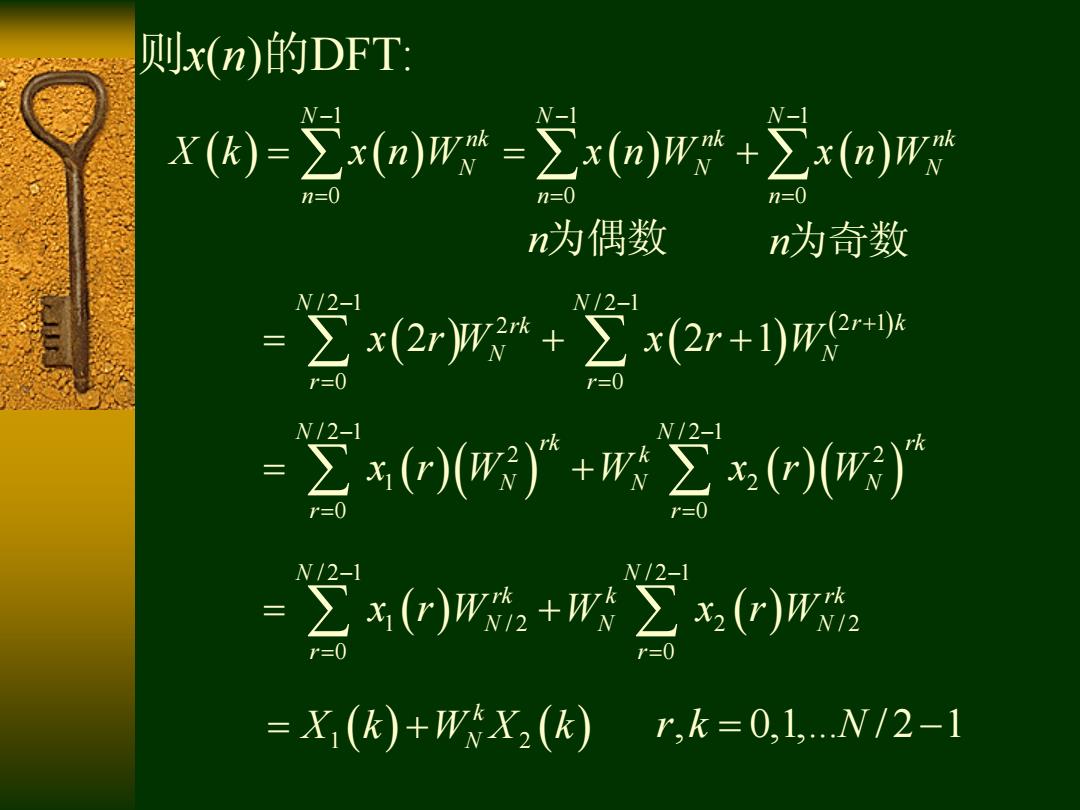
则x(n)的DFT: r)-上xa)g-∑xo)w+2o)w V- n=0 1n=0 n=0 n为偶数 n为奇数 N/2-1 N/2-1 x2rW+∑x(2r+）W r=0 空0对+三u N/2-1 N/2- N/2-1 =Σx(r）W+W∑x(r)W。 r=0 =X(k)+WX2 (k) r,k=0,1,N/2-1

则x(n)的DFT:         1 1 1 0 0 0 N N N nk nk nk N N N n n n X k x n W x n W x n W             n为偶数 n为奇数       / 2 1 / 2 1 2 2 1 0 0 2 2 1 N N rk r k N N r r x r W x r W                 / 2 1 / 2 1 2 2 1 2 0 0 N N rk rk k N N N r r x r W W x r W             / 2 1 / 2 1 1 / 2 2 / 2 0 0 N N rk k rk N N N r r x r W W x r W         1 2     k   X k W X k N r k N , 0,1,... / 2 1  

再利用周期性求()的后半部分 X(k),X2(k)是以N/2为周期的 x》-x因)-x) 又W=W2W攻=-W X(k)=X (k)+WX2(k) k=0,1,.,N/2-1 Xk+今）)=X()-mx,) X() X(因)+WX( X2(k) Xi(k)-W X2(k)

再利用周期性求X(k)的后半部分 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) 2 k N k N X k X k W X k N X k X k W X k           k N   0,1,..., /2 1         1 2 1 1 2 2 , / 2 2 2 X k X k N N N X k X k X k X k                  是以 为周期的 2 / 2 N k N k k W W W W N N N N  又   

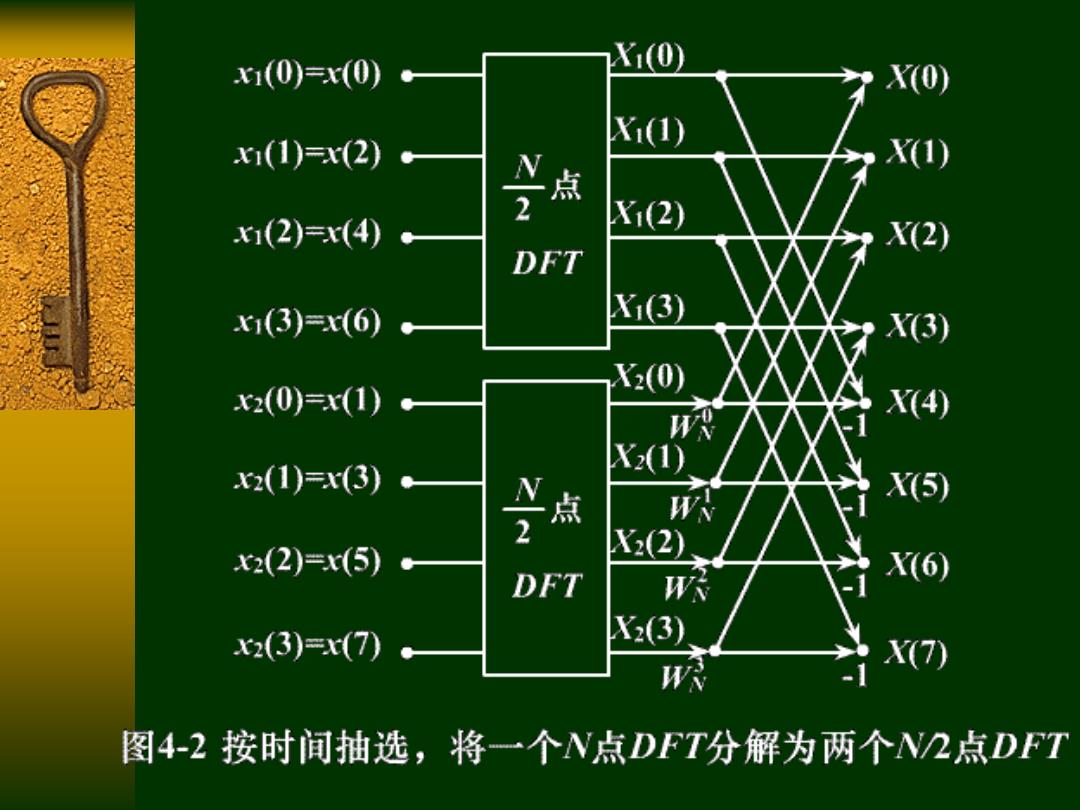
x1(0)=x(0) X(0) x1(1)=x(2) xd 0 点 x1(2)=x(4④) X1(2) DFT X2) x1(3)=x(6) X(3) x2(0)=x(1) x2(1)=x(3) 点 x2(2)=x(5) X(2) DET x2(3)=x(7) xG) X7) W 图4-2按时间抽选，将一个N点DFT分解为两个N2点DFT

分解后的运算量： 复数乘法 复数加法 一个N/2点DFT( N/2)2 N/2(N/2-1) 两个N/2点DFTN2/2 N(W/2-1) 一个蝶形 1 2 N/2个蝶形 N/2 N 总计 N2/2+N/2 N(N/2-1)+N ≈N2/2 ≈N2/2 运算量减少了近一半

分解后的运算量： 复数乘法 复数加法 一个N / 2点DFT (N / 2)2 N / 2 (N / 2 –1) 两个N / 2点DFT N 2 / 2 N (N / 2 –1) 一个蝶形 1 2 N / 2个蝶形 N / 2 N 总计 2 2 / 2 / 2 / 2 N N N     2 / 2 1 / 2 N N N N    运算量减少了近一半