中国地质大学（武汉）：《数字信号处理 Digital Signal Processing》课程教学资源（课件讲稿）第七章 FIR数字滤波器的设计方法

第七章R数字滤波器的设计方法 IR数字滤波器： 可以利用模拟滤波器设计 但相位非线性 FIR数字滤波器： 可以严格线性相位，又可任意幅度特性 因果稳定系统 可用FFT计算 但阶次比R滤波器要高得多

第七章 FIR数字滤波器的设计方法 IIR数字滤波器： 可以利用模拟滤波器设计 但相位非线性 FIR数字滤波器： 可以严格线性相位，又可任意幅度特性 因果稳定系统 可用FFT计算 但阶次比IIR滤波器要高得多

一、线性相位FIR滤波器的特点 FR滤波器的单位冲激响应： h(n)0≤n≤N-1 系统函数： N-1 H(a)=∑h(n)z" n=0 在z平面有N-1个零点 在z=0处是N-1阶极点

一、线性相位FIR滤波器的特点 FIR滤波器的单位冲激响应： h n n N ( ) 0 1    1 0 ( ) ( ) N n n H z h n z      系统函数： 在 z 平面有N –1 个零点 在 z = 0 处是N –1 阶极点

1、线性相位条件 h(n)为实序列时，其频率响应： H(e)=∑m)em=H(oeo)=±Hem)leo n=0 线性相位是指O(o)是0的线性函数 即群延时-@=：是常数 do 第一类线性相位：(0)=-⑩ 第二类线性相位：(0)=阝，-t0

h(n)为实序列时，其频率响应： 1、线性相位条件 ( ) ( ) j j H e e      即群延时 是常数 d ( ) d       0 第二类线性相位：    ( )   第一类线性相位：    ( )   1 0 ( ) ( ) N j j n n H e h n e        ( ) ( ) j H e     线性相位是指    是  的线性函数

2e=水”r38 n=0 第一类线性相位：(o)=-0 ±H(e)cos(or）=∑(n)cos(on) n=0 N- ±H(e)sn(or)=∑h(n)sin(on) h(n）sin(on） 8or)- 网 n=0 N-1 h(n)cos(on) n=0 ∑h(n)）sin(or)cos(om）-∑A(mcos(or)sin(onm）=0 2 Σ)sin[e-mo]-=0

( ) ( ) j j H e e      1 0 ( ) ( ) N j j n n H e h n e        第一类线性相位：    ( )   ( ) j j H e e            1 0 ( ) cos cos N j n H e h n n               1 0 ( ) sin sin N j n H e h n n                       1 0 1 0 sin sin cos cos N n N n h n n tg h n n                          1 1 0 0 sin cos cos sin 0 N N n n h n n h n n                1 0 sin 0 N n h n n           

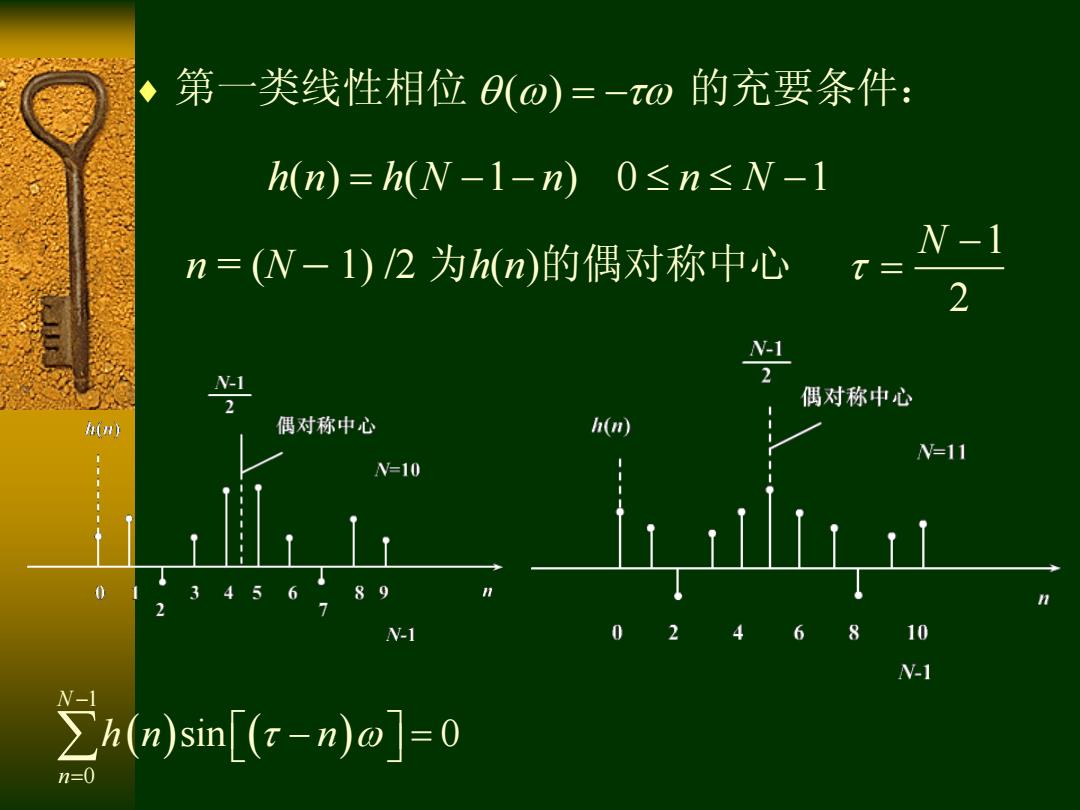
◆第一类线性相位0(o)=-x0的充要条件： h(n)=h(N-1-n0≤n≤N-1 n=(N-1)/2为h(n)的偶对称中心 N-1 t= 2 N-1 N-1 偶对称中心 h(n) 偶对称中心 h(n) N=11 W=10 0 45 89 N-1 2 6 8 10 N-1 ∑n(n)sin[(c-n)o]=0

 第一类线性相位    ( )   的充要条件： h n h N n n N ( ) ( 1 ) 0 1       1 2 N   n = (N – 1) /2 为h(n)的偶对称中心      1 0 sin 0 N n h n n           

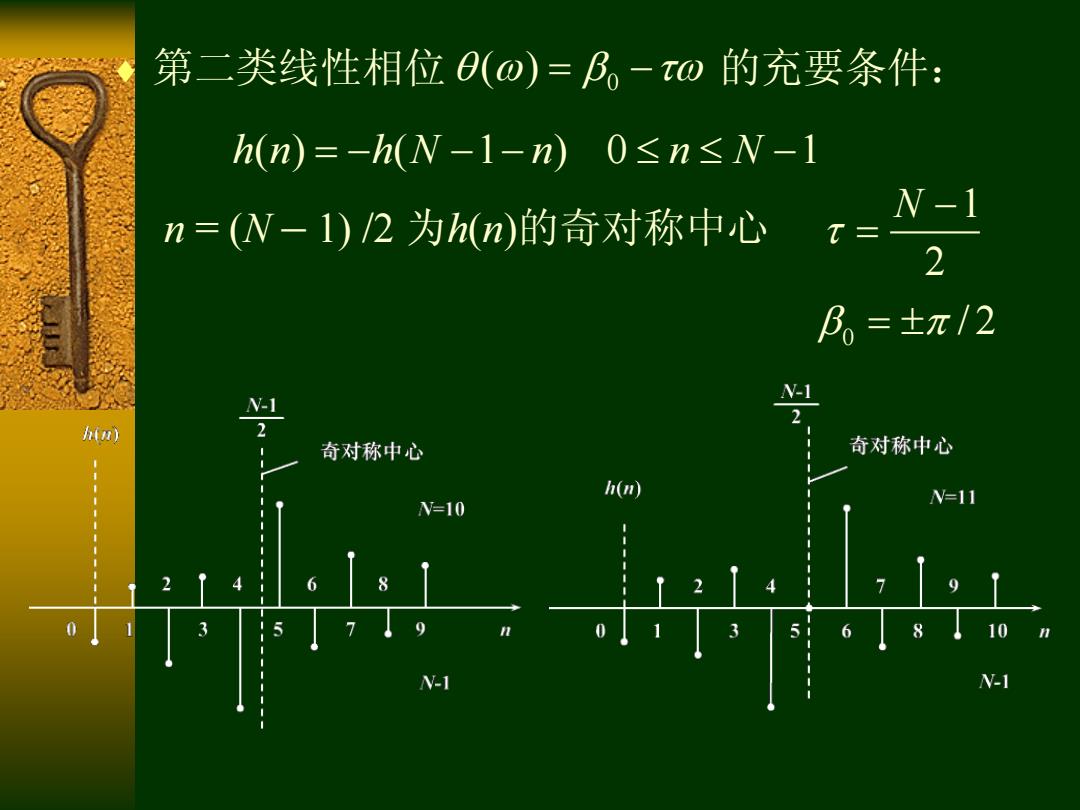
第二类线性相位(0)=B。-t0的充要条件： h(n)=-h(N-1-n)0≤n≤N-1 n=(N-1)2为h(n)的奇对称中心 t- N-1 2 B=±π/2 N-1 -1 hin) 奇对称中心 奇对称中心 h(m N=10 N=11 6 10 N-1 N-1

 第二类线性相位     ( )   0 的充要条件： h n h N n n N ( ) ( 1 ) 0 1        1 2 N    0     / 2 n = (N – 1) /2 为h(n)的奇对称中心

2、线性相位FR滤波器频率响应的特点 由(n)=±h(N-1-m)0≤n≤N-1 系统函数： He=∑hnE"-∑±hN-1-nE· n=0 令m=N-1-n =∑±h0mz- m=0 N-1 =±-w-∑(m)z m=0 =±zN-DH(z1)

2、线性相位FIR滤波器频率响应的特点 1 1 0 0 ( ) ( ) ( 1 ) N N n n n n H z h n z h N n z              1 ( 1 ) 0 ( ) N N m m h m z         ( 1) 1 ( ) N z H z      令m N n   1 系统函数： 由 h n h N n n N ( ) ( 1 ) 0 1        1 ( 1) 0 ( ) N N m m z h m z       

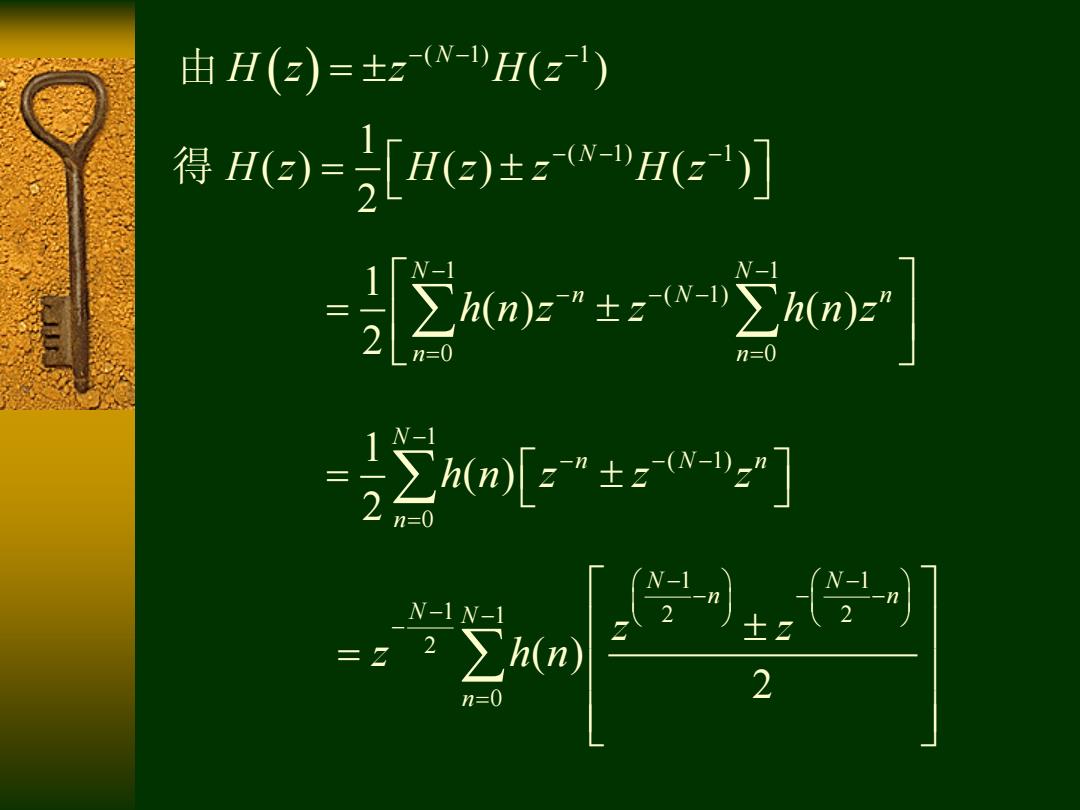
由H(e)=±zw-H(z) 得e)=)±：H] -2a生o] N-1 n=0 -[±] N-1N-1 =z?∑h(n) n=0 2

1 ( 1) 1 ( ) ( ) ( ) 2 N H z H z z H z        得   1 1 ( 1) 0 0 1 ( ) ( ) 2 N N n N n n n h n z z h n z                  1 ( 1) 0 1 ( ) 2 N n N n n h n z z z             1 1 1 1 2 2 2 0 ( ) 2 N N n n N N n z z z h n                                     ( 1) 1 ( ) N H z z H z    由  

N-1N-1 H(e)=z∑n) n=0 2 2 Z=ejo ete COSX= 2 N-1N- e H(e)=H(E) n=0 2as[〔

1 1 2 2 1 cos " " 2 2 1 sin " " 2 j N N n n z e N n z z N j n                                                               1 1 1 1 2 2 2 0 ( ) 2 N N n n N N n z z H z z h n                                   1 1 2 0 1 1 2 0 1 ( )cos 2 ( ) ( ) 1 ( )sin 2 j N N j j n z e N N j n N e h n n H e H z N je h n n                                                       " "  " "  cos 2 jx jx e e x   

1)h(n)偶对称 h(n)=h(N-1-n) ◆频率响应： eelL-:宁2ao W-1N-1 1: 相化图数：o=- o) 2 2π 0 0 为第一类线性相位 N-1 2 -π(N-1)

 频率响应： h n h N n ( ) ( 1 )    1 1 2 0 1 ( ) ( ) ( )cos 2 j N N j j z e n N H e H z e h n n                           1 2 N    1）h(n)偶对称 为第一类线性相位 1 ( ) 2 N     相位函数：  