
电磁场与电磁波 第1章失量分析合☒】 第1章矢量分析 一、矢量和标量的定义 二、矢量的运算法则 三、矢量微分元:线元,面元,体元 四、标量场的梯度 五、矢量场的散度 六、矢量场的旋度 七、重要的场论公式
电磁场与电磁波 第1章 矢量分析 第1章 矢量分析 一、矢量和标量的定义 二、矢量的运算法则 三、矢量微分元:线元,面元,体元 四、标量场的梯度 六、矢量场的旋度 五、矢量场的散度 七、重要的场论公式

电磁场与电磁波 第1章失量分析合☒ 一、矢量和标量的定义 1.标量:只有大小,没有方向的物理量。 如:温度T、长度L等 2.矢量:不仅有大小,而且有方向的物理量。 如:力疗、速度下、电场龙等 矢量表示为:A日Aa 其中:!为矢量的模,表示该矢量的大小。 à为单位矢量,表示矢量的方向,其大小为1。 所以:一个矢量就表示成矢量的模与单位矢量的乘积
电磁场与电磁波 第1章 矢量分析 一、矢量和标量的定义 1.标量:只有大小,没有方向的物理量。 矢量表示为: A A a | | ˆ 所以:一个矢量就表示成矢量的模与单位矢量的乘积。 其中: 为矢量的模,表示该矢量的大小。 为单位矢量,表示矢量的方向,其大小为1。 | A | a ˆ 2.矢量:不仅有大小,而且有方向的物理量。 如:力 F 、速度 v 、电场 E 等 如:温度 T、长度 L 等

电磁场与电磁波 第1章夫量分析 合 例1:在直角坐标系中,x方向的大小为6的矢量如何表示? 6à, y 图示法: 6a, x 力的图示法: F=FN+F G
电磁场与电磁波 第1章 矢量分析 例1:在直角坐标系中, x 方向的大小为 6 的矢量如何表示? 6 ˆ x a 图示法: 6 ˆ x a G FN Ff x y 力的图示法: F F F F N f
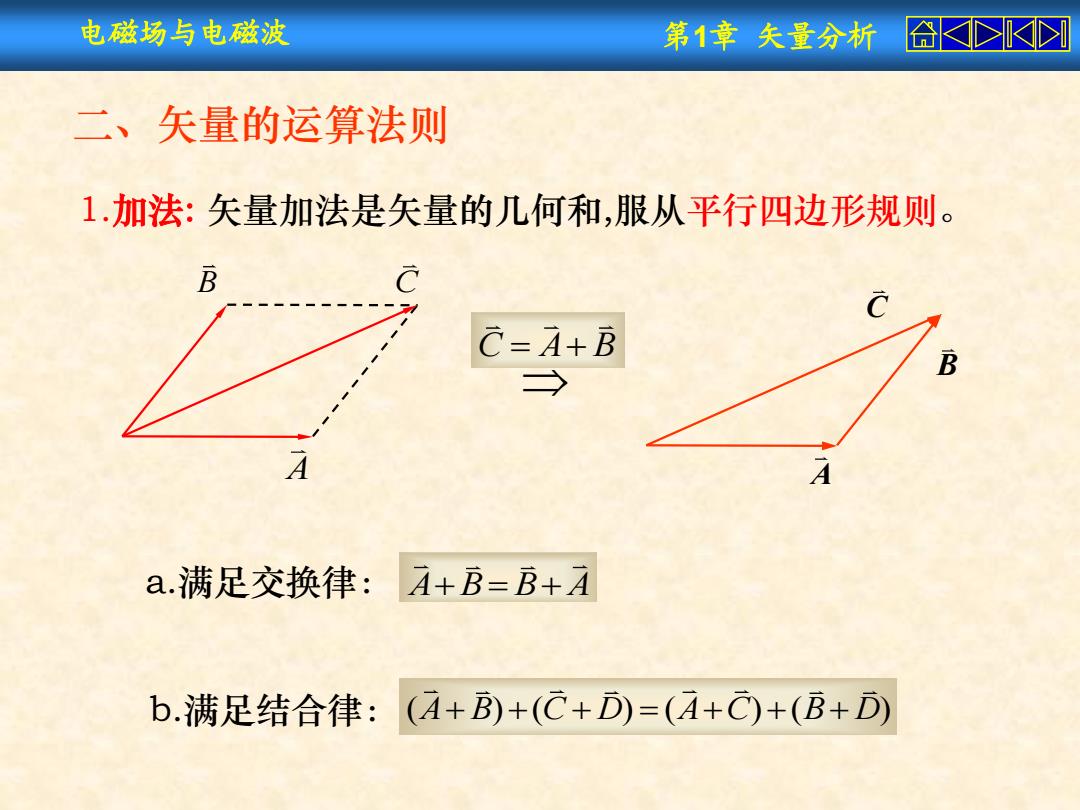
电磁场与电磁波 第1章失量分析合 二、矢量的运算法则 1.加法:矢量加法是矢量的几何和,服从平行四边形规则。 B C=4+B B → A a.满足交换律:A+B=B+A b.满足结合律:(A+B)+(C+D)=(A+C)+(B+D)
电磁场与电磁波 第1章 矢量分析 二、矢量的运算法则 1.加法: 矢量加法是矢量的几何和,服从平行四边形规则。 a.满足交换律: A B B A b.满足结合律: C A B B A C B A C ( ) ( ) ( ) ( ) A B C D A C B D

电磁场与电磁波 第1章失量分析囧 在直角坐标系下的矢量表示: 三个方向的单位矢量用ax,av,a表示。 A 根据矢量加法运算: 4=7+4,+4 其中: A=Aà,A=A,a,A=Aà 所以:A=Aa+A,a,+Aa
电磁场与电磁波 第1章 矢量分析 z o y x 三个方向的单位矢量用 a a a ˆ x y z , , ˆ ˆ 表示。 根据矢量加法运算: A A A A x y z ˆ , , ˆ ˆ A A a A A a A A a x x x y y y z z z 所以: ˆ ˆ ˆ A A a A a A a x x y y z z 在直角坐标系下的矢量表示: A A x Ay Az 其中:

电磁场与电磁波 第1章失量分析合☒】 矢量:A=Aa+A,a,+Aà ◆模的计算:1A=V4++A A +单位头量: 子合a+a清2 y =cosaa,+cos Ba,+cosya. +方向角与方向余弦:,阝,Y cosa 条= cosy= A 在直角坐标系中三个矢量加法运算: A+B+C=(A+B,+Cx)a+(A,+B,+C,)a,+(A+B.+C:)a
电磁场与电磁波 第1章 矢量分析 矢量: ˆ ˆ ˆ A A a A a A a x x y y z z 模的计算: 222 | | A A A A x y z 单位矢量: ˆ ˆ ˆ ˆ | | | | | | | | x y z x y z A A A A a a a a A A A A 方向角与方向余弦: , , | | , cos | | , cos | | cos A A A A A Ax y z cos cos cos ˆ ˆ ˆ x y z a a a 在直角坐标系中三个矢量加法运算: ( ) ( ) ( ) ˆ ˆ ˆ A B C A B C a A B C a A B C a x x x x y y y y z z z z z o y x A A x Ay Az

电磁场与电磁波 第1章失量分析 合 2减法:换成加法运算 D=4-B=4+(-B) 逆矢量:B和(-®)的模相等,方向相反,互为逆矢量。 B B 4+B+C=0 A 推论: 任意多个矢量首尾相连组成闭合多边形,其矢量和必为零。 在直角坐标系中两矢量的减法运算: A-B=(A.-B.)a+(A,-B,)a,+(A.-B.)a
电磁场与电磁波 第1章 矢量分析 2.减法:换成加法运算 D A B A B ( ) A B C B A B 逆矢量: B 和 ( ) B 的模相等,方向相反,互为逆矢量。 D B A D A B C 0 在直角坐标系中两矢量的减法运算: ( ) ( ) ( ) ˆ ˆ ˆ A B A B a A B a A B a x x x y y y z z z 推论: 任意多个矢量首尾相连组成闭合多边形,其矢量和必为零

电磁场与电磁波 第1章失量分析合☒】 3.乘法: (1)标量与矢量的乘积: k>0方向不变,大小为倍 kA=kAla k=0 k<0方向相反,大小为倍 (2)矢量与矢量乘积分两种定义 a.标量积(点积): A.B日A|B|cosO A +两矢量的点积含义: 一矢量在另一矢量方向上的投影与另一矢量模的乘积, 其结果是一标量
电磁场与电磁波 第1章 矢量分析 3.乘法: (1)标量与矢量的乘积: 0 | | 0 ˆ 0 k kA k A a k k 方向不变,大小为|k|倍 方向相反,大小为|k|倍 (2)矢量与矢量乘积分两种定义 a. 标量积(点积): A B A B | | | | cos B A 两矢量的点积含义: 一矢量在另一矢量方向上的投影与另一矢量模的乘积, 其结果是一标量

电磁场与电磁波 第1章夫量分析 合 推论1:满足交换律 A.B=B.A 推论2:满足分配律A·(B+C)=AB+A.C 推论3:当两个非零矢量点积为零,则这两个矢量必正交。 在直角坐标系中,已知三个坐标轴是相互正交的,即 a.·av=0,a.·a.=0,a,·a.=0 ax·ax=1,a·ay=1,aa.=1 有两矢量点积: A.B=(Aa+Aa+Aa)(B a,+B a,+Ba) =AxBx+A.By+4.B. 结论:两矢量点积等于对应分量的乘积之和
电磁场与电磁波 第1章 矢量分析 •在直角坐标系中,已知三个坐标轴是相互正交的,即 ˆ ˆ 0, 0, 0 ˆ ˆ ˆ ˆ ˆ ˆ 1, 1, 1 ˆ ˆ ˆ ˆ x y x z y z x x y y z z a a a a a a a a a a a a 有两矢量点积: ( ) ( ) ˆ ˆ ˆ ˆ ˆ ˆ A B A a A a A a B a B a B a x x y y z z x x y y z z Ax Bx Ay By Az Bz •结论: 两矢量点积等于对应分量的乘积之和。 推论1:满足交换律 推论2:满足分配律 推论3:当两个非零矢量点积为零,则这两个矢量必正交。 A B B A A B C A B A C ( )

电磁场与电磁波 第1章失量分析合 b.矢量积(叉积) B 4xB=4B|sina。 含义: A 两矢量叉积,结果得一新矢量,其大小为这两个矢量 组成的平行四边形的面积,方向为该面的法线方向,且三 者符合右手螺旋法则。 推论1:不服从交换律:A×B≠B×A AxB=-BxA 推论2:服从分配律:Ax(B+C)=AxB+AxC 推论3:不服从结合律:Ax(BxC)≠(A×B)×C 推论4:当两个非零矢量叉积为零,则这两个矢量必平行
电磁场与电磁波 第1章 矢量分析 推论1:不服从交换律: A B B A A B B A , 推论2:服从分配律: A B C A B A C ( ) 推论3:不服从结合律: A B C A B C ( ) ( ) 推论4:当两个非零矢量叉积为零,则这两个矢量必平行。 b.矢量积(叉积): | | | | sin ˆ A B A B a c •含义: 两矢量叉积,结果得一新矢量,其大小为这两个矢量 组成的平行四边形的面积,方向为该面的法线方向,且三 者符合右手螺旋法则。 B A ˆ c a