
第四章 网络定理 前几章介绍了几种常用的电路元件,电路的 基本定律和各种分析方法。本章介绍线性电阻电 路的几个网络定理,以便进一步了解线性电阻电 路的基本性质。利用这些定理可以简化电路的分 析和计算
第四章 网络定理 前几章介绍了几种常用的电路元件,电路的 基本定律和各种分析方法。本章介绍线性电阻电 路的几个网络定理,以便进一步了解线性电阻电 路的基本性质。利用这些定理可以简化电路的分 析和计算

§4-1叠加定理 由独立电源和线性电阻元件(线性电阻、线性受控源等) 组成的电路,称为线性电阻电路。描述线性电阻电路各电 压电流关系的各种电路方程,是以电压电流为变量的一组 线性代数方程。作为电路输入或激励的独立电源,其、和 i、总是作为与电压电流变量无关的量出现在这些方程的右 边。求解这些电路方程得到的各支路电流和电压(称为输出 或响应)是独立电源、和的线性函数。电路响应与激励之 问的这种线性关系称为叠加性,它是线性电路的一种基本 性质
§4-l 叠加定理 由独立电源和线性电阻元件(线性电阻、线性受控源等) 组成的电路,称为线性电阻电路。描述线性电阻电路各电 压电流关系的各种电路方程,是以电压电流为变量的一组 线性代数方程。作为电路输入或激励的独立电源,其uS和 i S总是作为与电压电流变量无关的量出现在这些方程的右 边。求解这些电路方程得到的各支路电流和电压(称为输出 或响应)是独立电源uS和i S的线性函数。电路响应与激励之 间的这种线性关系称为叠加性,它是线性电路的一种基本 性质
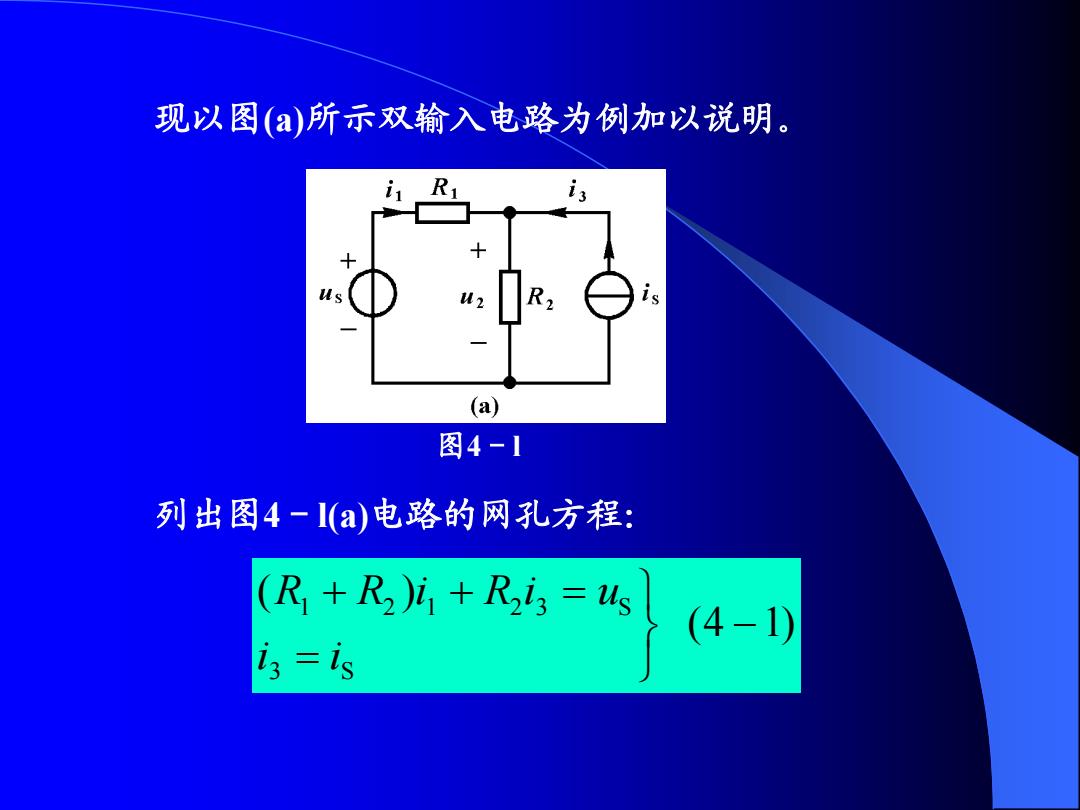
现以图(a)所示双输入电路为例加以说明。 us (a) 图4-1 列出图4-l(a)电路的网孔方程: (R1+R2)i1+R243=4s 13=is 4-)
现以图(a)所示双输入电路为例加以说明。 列出图4-l(a)电路的网孔方程: (4 1) ( ) 3 S 1 2 1 2 3 S i i R R i R i u 图4-l

(R,+R2)i1+R23=“s (4-1) is =is 求解上式可得到电阻R的电流,和电阻R2上电压42 -R2 4s+ s=1+i (4-2)》 R+R R+R 其中 =li+R 一ls R+R
求解上式可得到电阻R1的电流i 1和电阻R2上电压u2 (4 2) 1 " 1 ' S 1 1 2 2 S 1 2 1 i i i R R R u R R i 其中 S 1 2 2 1 0 " 1 S 1 2 1 0 ' 1 S S 1 i R R R i i u R R i i u i (4 1) ( ) 3 S 1 2 1 2 3 S i i R R i R i u
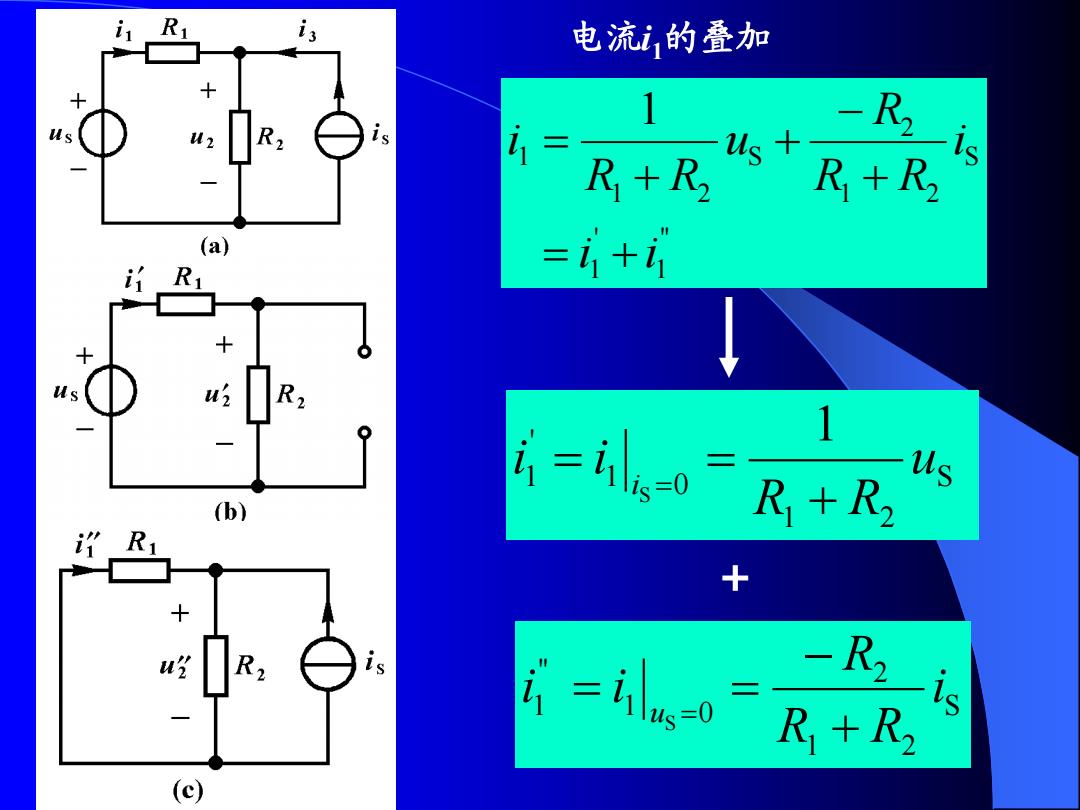
i R is 电流i,的叠加 1 -R2 us R+R s+ R+R2 9 (a) =1+i i=+ us (b) ”R1 + -R2 R+R2 (c)
" 1 ' 1 S 1 2 2 S 1 2 1 1 i i i R R R u R R i + S 1 2 2 1 0 " 1 S i R R R i i u 1 S 1 2 1 0 ' 1 S u R R i i i 电流i1的叠加
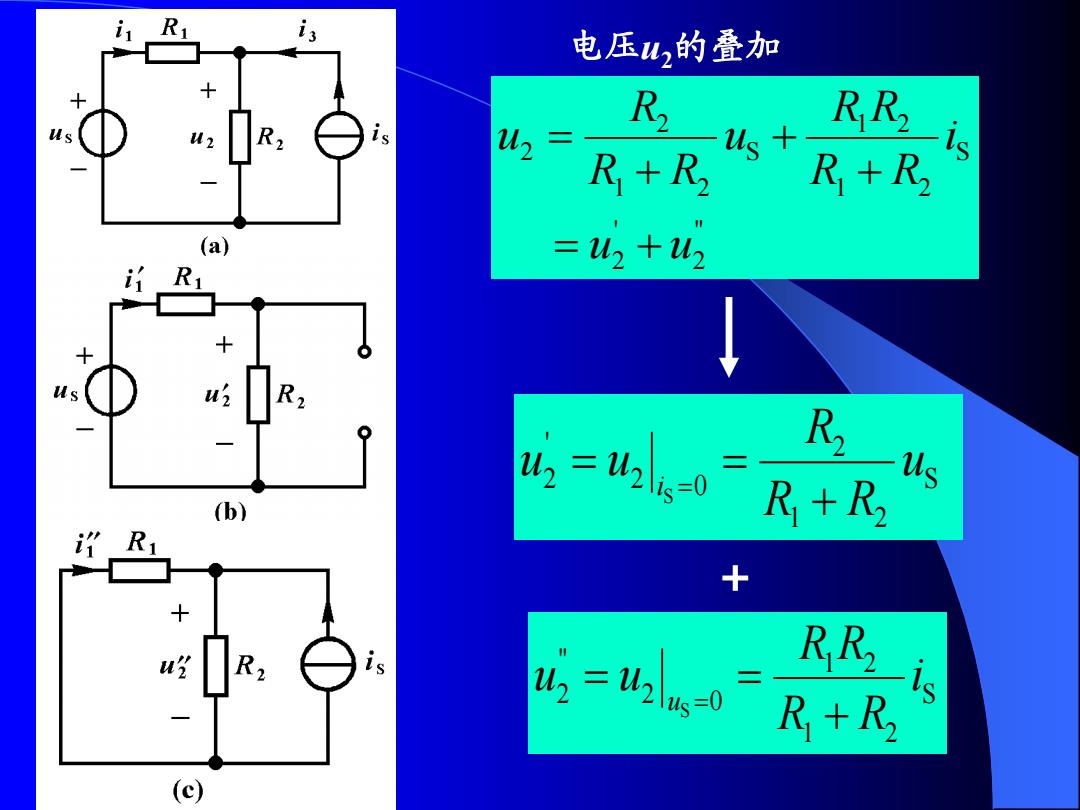
i is 电压u2的叠加 R RR2 us 2= R+R2 us R+R2 (a) =u2+u2 =460 R2一ls (b) R+R, ”R1 + + 4=42s-0 RR2 R+R2 (c)
+ " 2 ' 2 S 1 2 1 2 S 1 2 2 2 u u i R R R R u R R R u S 1 2 2 0 2 ' 2 S u R R R u u i S 1 2 1 2 0 2 " 2 S i R R R R u u u 电压u2的叠加

从上可见:电流i和电压42均由两项相加而成。 第一项i和?是该电路在独立电流源开路(、=0)时, 由独立电压源单独作用所产生的i,和42。 第二项i”和u%是该电路在独立电压源短路(4、=0)时, 由独立电流源单独作用所产生的和42 以上叙述表明,由两个独立电源共同产生的响应,等 于每个独立电源单独作用所产生响应之和。线性电路的这 种叠加性称为叠加定理
从上可见:电流i 1和电压u2均由两项相加而成。 第一项i 1 和u 2是该电路在独立电流源开路(i S =0)时, 由独立电压源单独作用所产生的i 1和u2。 第二项i 1和u 2是该电路在独立电压源短路(uS =0)时, 由独立电流源单独作用所产生的i 1和u2。 以上叙述表明,由两个独立电源共同产生的响应,等 于每个独立电源单独作用所产生响应之和。线性电路的这 种叠加性称为叠加定理

叠加定理陈述为:由全部独立电源在线性电阻电路中 产生的任一电压或电流,等于每一个独立电源单独作用所 产生的相应电压或电流的代数和。 也就是说,只要电路存在惟一解,线性电阻电路中的 任一结,点电压、支路电压或支路电流均可表示为以下形式 y=H4s1+H24s2+…+Hnm4sm+Ks1+K2is2+…+Kns (4-4 式中4sx(k-1,2,m)表示电路中独立电压源的电压; isx(=1,2,,n)表示电路中独立电流源的电流。 Hx(k=1,2,,m)和Kk(k=1,2,,m)是常量,它们取决 于电路的参数和输出变量的选择,而与独立电源无关
叠加定理陈述为:由全部独立电源在线性电阻电路中 产生的任一电压或电流,等于每一个独立电源单独作用所 产生的相应电压或电流的代数和。 也就是说,只要电路存在惟一解,线性电阻电路中的 任一结点电压、支路电压或支路电流均可表示为以下形式 (4 - 4) 1 S1 2 S2 m Sm 1 S1 2 S2 n Sn y H u H u H u K i K i K i 式中uSk (k=1,2,…,m)表示电路中独立电压源的电压; i Sk (k=1,2,…,n)表示电路中独立电流源的电流。 Hk (k=1,2,…,m)和Kk (k=1,2,…,n)是常量,它们取决 于电路的参数和输出变量的选择,而与独立电源无关

在计算某一独立电源单独作用所产生的电压或电流时, 应将电路中其它独立电压源用短路(、=O)代替,而其它独 立电流源用开路(、=0)代替。 式(4-4)中的每项(us尸H4s或s尺K,s是该独 立电源单独作用,其余独立电源全部置零时的响应。这表 明r(usx)与输入4s或y(is)与输入isx之间存在正比例关系, 这是线性电路具有“齐次性” 的一种体现。 式(4一4)还表明在线性电阻电路中,由几个独立电源 共同作用产生的响应,等于每个独立电源单独作用产生的 响应之和,这是线性电路具有可“叠加性”的一种体现。 利用叠加定理反映的线性电路的这种基本性质,可以简化 线性电路的分析和计算,在以后的学习中经常用到
在计算某一独立电源单独作用所产生的电压或电流时, 应将电路中其它独立电压源用短路(uS =0)代替,而其它独 立电流源用开路(i S =0)代替。 式(4-4)中的每一项y(uSk )=Hk uSk或y(i Sk )=Kk i Sk是该独 立电源单独作用,其余独立电源全部置零时的响应。这表 明y(uSk )与输入uSk或y(i Sk )与输入i Sk之间存在正比例关系, 这是线性电路具有“ 齐次性” 的一种体现。 式(4-4)还表明在线性电阻电路中,由几个独立电源 共同作用产生的响应,等于每个独立电源单独作用产生的 响应之和,这是线性电路具有可“ 叠 加性” 的一种体现。 利用叠加定理反映的线性电路的这种基本性质,可以简化 线性电路的分析和计算,在以后的学习中经常用到

需要说明的是叠加定理仅仅适用于存在惟一解的线性电路。 值得注意的是:线性电路中元件的功率并不等于每个独 立电源单独产生功率之和。例如在双输入电路中某元件吸收 的功率 =ui=(u +u )(i +i) =ui+ui+ui+ui ≠ui+ui=p1+P2
值得注意的是:线性电路中元件的功率并不等于每个独 立电源单独产生功率之和。例如在双输入电路中某元件吸收 的功率 1 2 ' ' " " ' ' ' " " ' " " ' " ' " ( )( ) u i u i p p u i u i u i u i p ui u u i i 需要说明的是叠加定理仅仅适用于存在惟一解的线性电路