
数字电子技术基础 第一章 数字逻辑基础
数字电子技术基础 第一章 数字逻辑基础

1.1脉冲信号及其参数 模拟信号和数字信号 模拟量一自然界存在的随时间连续变化的 物理量, ■ 1、模拟信号 与自然物理量成线性关系的 电信号,幅度随时间连续变化。 例: 非周期性模拟信号(温度、压力等) 主要参数:幅度的大小 周期性模拟信号(正弦信号、锯齿波信号) 一主要参数:幅度、频率和周期
1.1脉冲信号及其参数 模拟信号和数字信号 模拟量——自然界存在的随时间连续变化的 物理量, 1、模拟信号——与自然物理量成线性关系的 电信号,幅度随时间连续变化。 例: 非周期性模拟信号(温度、压力等) ——主要参数:幅度的大小 周期性模拟信号(正弦信号、锯齿波信号) ——主要参数:幅度、频率和周期

2.数字信号---幅度大小在时间上离散变化 脉冲信号 周期性的、具有高、低两种幅值的离散电信。 参数: 1、周期T 信号变化一个循环的时间。 频率f (脉冲重复率PRR),每秒时间中的脉冲周期数。 2、脉冲幅度Vm—信号的最大变化值。 低电平VL一信号的低幅值 高电平V 信号的高幅值 Vm=Vn-VL 3、) 脉冲宽度Tw 信号从上升到50%Vm至下降到50%Vm所需的 时间(或高电平时间) 4、上升时间tr、-信号从10%Vm起上升到90%Vm所需的时间 5、下降时间tf.--信号从90%Vm起下降到10%Vm所需的时间 6、 占空比q--脉宽与周期之百分比:q=(Tw/T)%
2.数字信号------幅度大小在时间上离散变化 脉冲信号 ——周期性的、具有高、低两种幅值的离散电信。 参数: 1、周期T——信号变化一个循环的时间。 频率f——(脉冲重复率PRR),每秒时间中的脉冲周期数。 2、脉冲幅度Vm——信号的最大变化值。 低电平VL——信号的低幅值 高电平VH——信号的高幅值 Vm=VH-VL 3、脉冲宽度Tw——信号从上升到50%Vm至下降到50%Vm所需的 时间(或高电平时间) 4、上升时间tr、-----信号从10%Vm起上升到90%Vm所需的时间 5、下降时间tf-----信号从90%Vm起下降到10%Vm所需的时间 6、占空比q------脉宽与周期之百分比:q = (Tw / T) %

1.2数字乐统中数的表示方法 1.2.1 数制 进位计数制基本表示法 基本要素 基数和位权 1、位置记数法: 每个数码K所代表的数值与其所在位有关, 括 号外的下标表示其计数制(基数)值。 (N)R=(Kn-Kn-2.....KK0.KK2...)R 整数部分 小数部分 基数=数码的个数 位权=数码所在位的数值大小, 第i位的位权为基数的次幂。 整数部分为正幂、小数部分为负幂
1.2数字系统中数的表示方法 1.2.1 数制 一、进位计数制基本表示法 基本要素——基数和位权 1、位置记数法: 每个数码Ki所代表的数值与其所在位有关,括 号外的下标表示其计数制(基数)值。 (N)R=(Kn-1Kn-2…..K1K0 . K-1K-2……) R 整数部分 小数部分 基数 = 数码的个数 位权= 数码所在位的数值大小,第i位的位权为基数的i 次幂。 整数部分为正幂、小数部分为负幂

2、多项式展开表示法 各位数码乘以其所在位的位权相加后得其数 值(用十进制表示)。 (N)R=Kn-1Rm-1+Kn-2Rm-2+.....+KR1+KoRO 整数部分 +KR1+K2R2+. 小数部分 二、常用计数体制 l、十进制(Decimal) (N)10=(Dn-iDn-2D0D.D-2…)10 (271.59)10= 2×102十7×101十1×100十5×10-1十9×10-2
2、多项式展开表示法 各位数码乘以其所在位的位权相加后得其数 值(用十进制表示)。 (N)R=Kn-1Rn-1+Kn-2Rn-2+….. + K1R1+ K0R0 整数部分 + K-1R-1 + K-2R-2 +…… 小数部分 二、常用计数体制 1、十进制(Decimal) (N)10= (Dn-1Dn-2...D0.D-1D-2.. ) 10 (271.59)10= 2×102十7×101十1×100十5×10-1十9×10-2

2、二进制(Binary) 基数:2 位权:2 数符B:0、1(可以用低、高电平表示) 位置表示法:(N)2=(Bn-1Bn-2B0BB2.)2 按权展开式: (N)2=Bm-12n-1+Bn-22n-2++B20+B12-1+B.22-2+ 例:(1101.101)2= 1×23+1×22+0×21+1×20+1×21+0×2-2+1×2-3 =8+4+0+1+0.5+0+0.125=(13.625)10
2、二进制(Binary) 基数 : 2 位权:2 i 数符Bi: 0、1 (可以用低、高电平表示) 位置表示法:(N)2 =( Bn-1Bn-2...B0.B-1B-2.. ) 2 按权展开式: (N)2=Bn-12 n-1+Bn-22 n-2+...+B02 0+B-12 -1+B-22 -2+... 例: (1101.101)2= 1×2 3+1×2 2+0×2 1+1×2 0+1×2 -1+0×2 -2+1×2 -3 =8+4+0+1+0.5+0+0.125 = (13.625)10
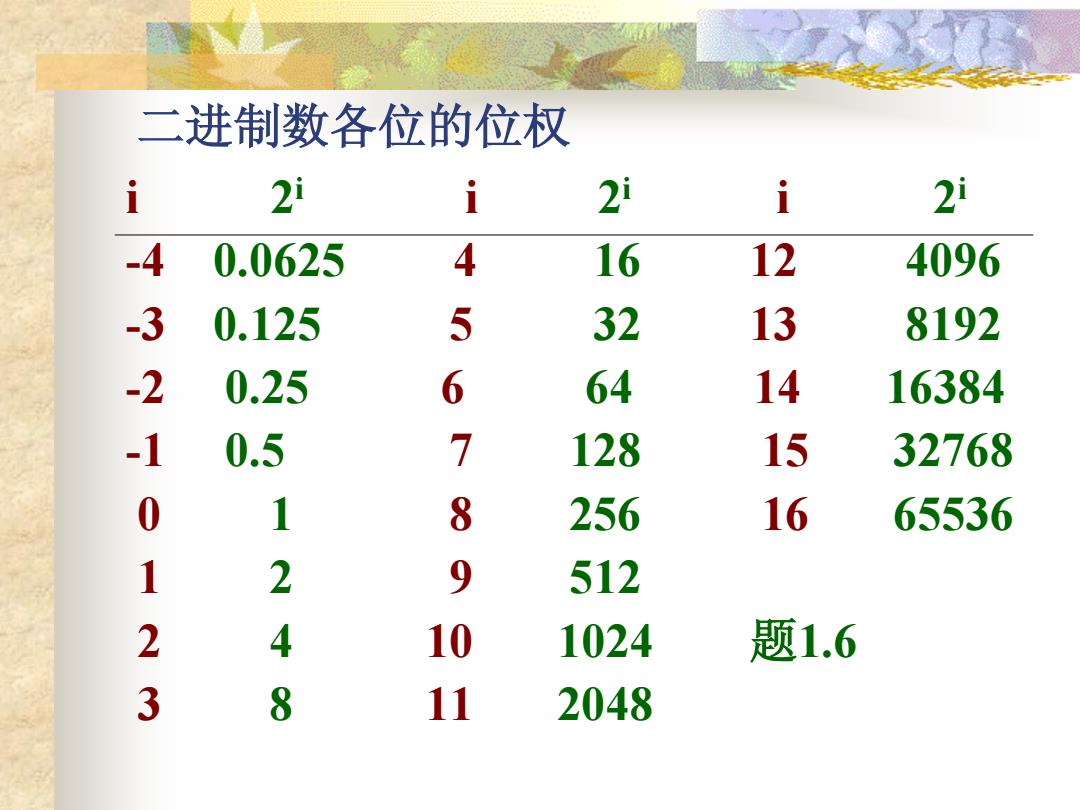
二进制数各位的位权 i 2i i 21 i 2i -4 0.0625 4 16 12 4096 -3 0.125 5 32 13 8192 -2 0.25 6 64 14 16384 -1 0.5 7 128 15 32768 0 1 8 256 16 65536 1 2 9 512 2 4 10 1024 题1.6 3 8 11 2048
二进制数各位的位权 i 2 i i 2 i i 2 i -4 0.0625 4 16 12 4096 -3 0.125 5 32 13 8192 -2 0.25 6 64 14 16384 -1 0.5 7 128 15 32768 0 1 8 256 16 65536 1 2 9 512 2 4 10 1024 题1.6 3 8 11 2048

二进制数的运算: 加法:逢二本位归零,高位加一。 (10110)2+(1101)2=(100011)2 减法:不够减本位借二,高位退一。 (10110)2-(1101)2=(1001)2 乘法:被乘数根据乘数各位为1的数码的位序移位 次并相加。 积的位数等于被乘数位数及乘数位数之和。 (10110)2×(1101)2=(100011110)2
二进制数的运算: 加法:逢二本位归零,高位加一。 (10110)2+(1101)2= (100011)2 减法:不够减本位借二,高位退一。 (10110)2-(1101)2= (1001)2 乘法:被乘数根据乘数各位为1的数码的位序i移位 i次并相加。 积的位数等于被乘数位数及乘数位数之和。 (10110)2× (1101)2= (100011110)2

3、八进制(Octal) 基数:8 位权:8i 数码0: 0、1、2、3、4、5、6、7 位置表示法:(N)8=(0m-10n-2000.102.)8 按权展开式: (N)8=0m-18m-1+0n-28m-2+.+0080+0.18-1+0.28-2+. 例: (172.54)8= 1×82+7×81+2×80+5×8-1+4×8-2 =64+56+2+0.625+0.0625=(122.6875)10
3、八进制(Octal) 基数:8 位权: 8 i 数码Oi: 0、1、2、3、4、5、6、7 位置表示法:(N)8 = (On-1On-2...O0.O-1O-2.. ) 8 按权展开式: (N)8=On-18 n-1+On-28 n-2+...+O08 0+O-18 -1+O-28 -2+... 例: (172.54)8= 1×8 2+7×8 1+2×8 0+5×8 -1+4×8 -2 =64+56+2+0.625+0.0625 = (122.6875)10

4、十六进制数(Hexadecimal) 基数:16 位权:161 数码H: 0、1、2、3、4、5、6、7、8、9、 A、B、C、D、E、F (10、11、12、13、14、15) 位置表示法:N)16=(Hn-Hn-2H0HH2)16 按权展开式: N2=Hn-116m-1+Hm-216m-2+.+H016+HL116-1+H216-2+.… (C07.A4)16=(C07.A4)HFC07.A4H= 12×162+0×161+7×160+10×16-1+4×16-2 =3072+0+7+0.625+0.015625=(3079.640625)10
4、十六进制数(Hexadecimal) 基数:16 位权: 16 i 数码Hi: 0、1、2、3、4、5、6、7、8、9、 A、 B、 C、 D、 E、 F (10、11、12、13、14、15) 位置表示法:(N)16 = (Hn-1Hn-2...H0.H-1H-2..) 16 按权展开式: (N)2=Hn-116n-1+Hn-216n-2+...+H0160+H-116-1+H-216-2+... (C07.A4)16= (C07.A4)H= C07.A4H= 12×162+0×161+7×160+10×16-1+4×16-2 =3072+0+7+0.625+0.015625 = (3079.640625)10