中国地质大学（武汉）：《电磁场与电磁波 Electromagntic Fields and Electromagntic waves》课程教学资源（课件讲稿）第8章 电磁波的辐射

电磁场与电磁波 第8章电磁波的辐射 合≤KI 第8章1 电磁波的辐射 一、辐射的基本概念 二、滞后位 三、电偶极子的辐射 四、磁偶极子的辐射 五、对称振子天线的辐射 六、天线阵的辐射

电磁场与电磁波 第8章 电磁波的辐射 第8章 电磁波的辐射 一、辐射的基本概念 二、滞后位 三、电偶极子的辐射 四、磁偶极子的辐射 五、对称振子天线的辐射 六、 天线阵的辐射

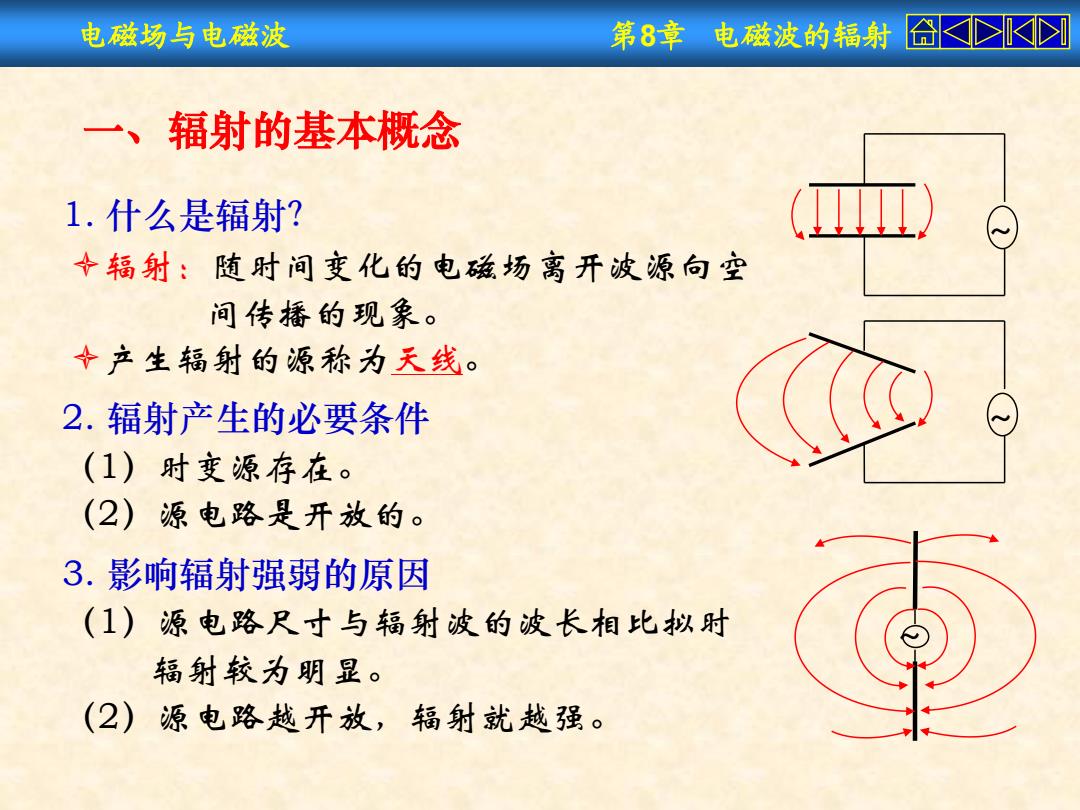
电磁场与电磁波 第8章电磁波的辐射合≤K 一、辐射的基本概念 1.什么是辐射？ 十辐射：随时间变化的电磁场离开波源向空 间传播的现象。 +产生辐射的源称为天线。 2.辐射产生的必要条件 (1)时变源存在。 (2)源电路是开放的。 3.影响辐射强弱的原因 (1)源电路尺寸与辐射波的波长相比拟时 辐射较为明显。 (2)源电路越开放，辐射就越强

电磁场与电磁波 第8章 电磁波的辐射 1. 什么是辐射？ 辐射：随时间变化的电磁场离开波源向空 间传播的现象。 产生辐射的源称为天线。 2. 辐射产生的必要条件 （1）时变源存在。 （2）源电路是开放的。 3. 影响辐射强弱的原因 （1）源电路尺寸与辐射波的波长相比拟时 辐射较为明显。 （2）源电路越开放，辐射就越强。 ~ ~ ~ 一、辐射的基本概念

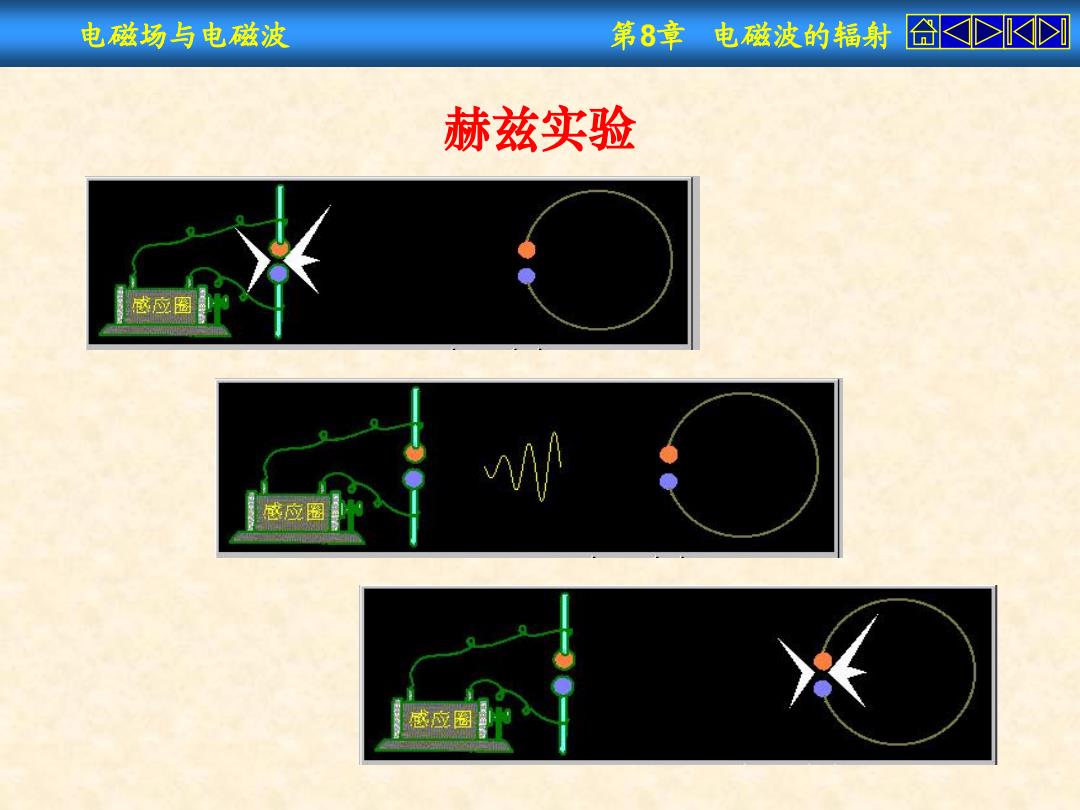
电磁场与电磁波 第8章电磁波的辐射 合≤KI 赫兹实验 感应圈 感应圈 感应圈

电磁场与电磁波 第8章 电磁波的辐射 赫兹实验

电磁场与电磁波 第8章 电磁波的辐射 合≤KI 电，偶极子的辐射演示 雷达探测且标演示

电磁场与电磁波 第8章 电磁波的辐射 电偶极子的辐射演示 雷达探测目标演示

电磁场与电磁波 第8章电磁波的辐射 合KDKI 二、滞后位 1.在静态场情况下，矢量位和标量位方程为 V2A=-uJ 70=- P 其解为：A∫dy [eav' 4πJ'R = 、JR 2.在时变场情况下，动态矢量位和动态标量位满足的方程 麦克斯韦方程： 7xH=Je+ε E 已知：B=V×AA=(V×) 龙=-7φ- 8t VXE 6B -E-0xA-x+=0一E+ A 8t 得：rw×动=+(w2 L

电磁场与电磁波 第8章 电磁波的辐射 二、滞后位 2. 在时变场情况下，动态矢量位和动态标量位满足的方程 1. 在静态场情况下，矢量位和标量位方程为 2    A J  d 4π V J A V R      1 d 4π V V R        其解为: 2       C t t              E H J B E 麦克斯韦方程： B A   E A ( ) t       ( ) 0 A E t      A E t      + A E t      = 1 H A   ( )  得： 1 ( ) ( ) C A A J t t               + 已知：

电磁场与电磁波 第8章电磁波的辐射 合≤K 利用矢量恒等式：V×V×A=V(V.①-VA xn=人+-0一7--氏+8s曾 62A I 洛仑兹规范：又·A+u a9=0 2A 8t V2A-u8 --HJc) 达朗贝尔方程 同理：V.E=PLVb-6 20 对于正弦时变场，时间因子为：ejo1 令：k2=o2u8 V2A+k2A=-uJc 1 dy' 方程的解为： R V2b+kb=-匹 川起发d

电磁场与电磁波 第8章 电磁波的辐射 2 2 2 V t            对于正弦时变场，时间因子为： j e  t 2 2 C 2 2 V k k              A A J 令： 2 2 k   利用矢量恒等式： 2        A A A ( ) 2 2 2 C ( ) A A J A t t                + A 0 t        洛仑兹规范： C 1 ( ) ( ) A A J t t               + 2 2 2 C t         A A J V E   同理：   达朗贝尔方程   j( ) C e d ' 4 t kR V R,t V R        J A   j( t ) 1 e , d ' 4 kR V V R t V R          方程的解为：

电磁场与电磁波 第8章电磁波的辐射 合KDKI 3.由A(R,)和(R)的表示式可知 acar 观察点 R R 人A dv' R 波源 ◆场点R处的A和中变化的相位较其源方和P落后ot-kR。 +该相位用时间表示：m-kR=t-人风)=o-=o-t) 式中t'=R/v就是波源j或P的变化传递到观察点所需 要的时间。 ◆距离波源R处在t时刻A(R,)和(R,)由前一时刻(t-t)的电流j 和电荷密度p的值决定。因此将A(R,)和(R,)称为滞后位

电磁场与电磁波 第8章 电磁波的辐射 3. 由 AR t,  和  R t,  的表示式可知  场点R处的 A 和  变化的相位较其源 J 和  落后 t kR  。  该相位用时间表示： ( ) ( ) ( ') k R t kR t R t t t v             式中 就是波源 或 的变化传递到观察点所需 要的时间。 t R v ' /  J  距离波源R处在t 时刻 和 由前一时刻 的电流 和电荷密度 的值决定。因此将 和 称为滞后位。 AR t,  J  AR t,   R t,   R t,  t t   波源 观察点 R   j( ) C e d ' 4 t kR V R,t V R        J A   j( ) 1 e , d ' 4 t kR V V R t V R         

电磁场与电磁波 第8章电磁波的辐射囧≤K】 三、电偶极子的辐射 1.什么是电偶极子？ +一段通有高频电流的直导线，当导线长度远远小于波长时， 该导线被称为电偶极子。 +当：1/九<<1，可近似地认为导线上每一点的电流都是 等幅同相的。 2.电偶极子的辐射场 （Ⅻ）电每极子的滞后位A约=会上' -dv R 如图所示，已知电流元

电磁场与电磁波 第8章 电磁波的辐射 三、电偶极子的辐射 1. 什么是电偶极子？ 一段通有高频电流的直导线，当导线长度远远小于波长时， 该导线被称为电偶极子。 当： , 可近似地认为导线上每一点的电流都是 等幅同相的。 l / 1   2. 电偶极子的辐射场 （1）电偶极子的滞后位   j C e d ' 4 kR V R V R       J A 如图所示, 已知电流元 C d d d ˆ ˆ z z I I l S l V S a a J     x y z l  P R  A

电磁场与电磁波 第8章电磁波的辐射 合≤DK>I A- dla.=ull e-ikR A 4元R AR Ag =A.cos0 在球坐标系 Ao=-A.sin A。=0 y Ax= ull e-ikR coSθ 4元 R 4,=- Lill e-ik sin O 4元R

电磁场与电磁波 第8章 电磁波的辐射 x y z l  P R  j j e e d ˆ ˆ 4π 4π kR kR z z l I Il l R R         A a a 在球坐标系 cos sin 0 R z z A A A A A              j e cos 4π kR R Il A R      j e sin 4π kR Il A R        A z AR a ˆ  A

电磁场与电磁波 第8章电磁波的辐射 合KDK (2)电偶极子的电磁场 aR Rao Rsinea 磁场由： B-x利R a a u R2sin aR a0 00 AR RAp 0 「HR=H。=0 得： 你气k日0 电场由： 7×i= 一E=d a龙 VxH 8t ER=-j cos@ 得： + E。=-j4元0sR sin E。=0

电磁场与电磁波 第8章 电磁波的辐射 磁场由：      E H = t j 0 e 1 j sin 4 R kR H H Il H k R R                得: （2）电偶极子的电磁场 2 ˆ ˆ sin ˆ 1 1 1 ( ) sin 0 R R R R R R A RA                    a a a H A 电场由： 得: j 2 j 2 2 e 1 j j cos 2 e j 1 j sin 4 0 kR R kR Il E k R R Il k E k R R R E                                1 j E H   