
第六节逻辑函数的卡诺图化简法 2.6.1用卡诺图表示逻辑函数 利用卡诺图化简逻 必什么是卡诺图 辑函数,简捷直观 逻辑函数的卡诺图是一个特定 灵活方便且易于确 的方格图。每一个小方格代表 定是否已得到最简 了逻辑函数的最小项,且任意 结果。 两个相邻小方格所代表的最小 卡诺图是真值 项只有一个变量之差 表的一种特殊形式 ®卡洛图把逻辑函数中的逻辑相 是化简逻辑函数的 邻与几何相邻一一对应在方格 重要工具。 图
第六节 逻辑函数的卡诺图化简法 ❖ 什么是卡诺图 逻辑函数的卡诺图是一个特定 的方格图。每一个小方格代表 了逻辑函数的最小项,且任意 两个相邻小方格所代表的最小 项只有一个变量之差。 卡洛图把逻辑函数中的逻辑相 邻与几何相邻一一对应在方格 图。 利用卡诺图化简逻 辑函数,简捷直观, 灵活方便且易于确 定是否已得到最简 结果。 卡诺图是真值 表的一种特殊形式, 是化简逻辑函数的 重要工具。 2.6.1 用卡诺图表示逻辑函数
1、卡诺图的构成 将逻辑函数真值表中的最小项重新排列成矩阵形式,并且 使矩阵的横方向和纵方向的逻辑变量的取值按照格雷码的顺序 排列,这样构成的图形就是卡诺图。 项与它相邻 00 01 11 小项有两个最小 B 10 每个2变量的最 m 项与它相邻 m5 小项有3个最小 每个3变量的最 变量卡诺图 3交量卡诺图 卡诺图的特点是任意两个相邻的最小项在图中也是相邻的 。 (相邻项是指两个最小项只有一个因子互为反变量,其余因子均 相同,又称为逻辑相邻项)
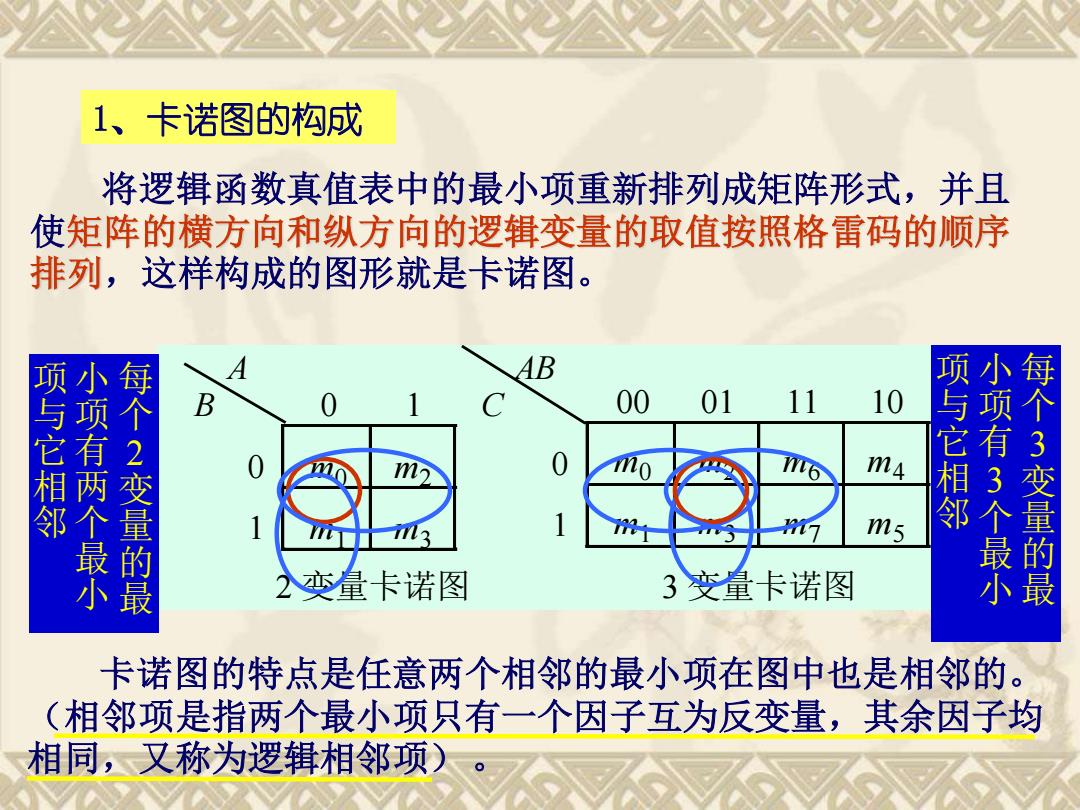
1、卡诺图的构成 将逻辑函数真值表中的最小项重新排列成矩阵形式,并且 使矩阵的横方向和纵方向的逻辑变量的取值按照格雷码的顺序 排列,这样构成的图形就是卡诺图。 卡诺图的特点是任意两个相邻的最小项在图中也是相邻的。 (相邻项是指两个最小项只有一个因子互为反变量,其余因子均 相同,又称为逻辑相邻项)。 A B 0 1 0 m0 m2 1 m1 m3 AB C 00 01 11 10 0 m0 m2 m6 m4 1 m1 m3 m7 m5 2 变量卡诺图 3 变量卡诺图 每 个 2 变 量 的 最 小 项 有 两 个 最 小 项 与 它 相 邻 每 个 3 变 量 的 最 小 项 有 3 个 最 小 项 与 它 相 邻
每个4变量的最小项有4个最小项与它相邻 B 项也是相邻的 00 10 最右列的相应最小 最左列的最小项与 00 m m8 01 mo 11 m3 m15 m11 袭 的 项与最下面一行的 最上面一行的最小 10 m2 m6 m14 m10 4变量卡诺图 两个相邻最小项可以合并消去一个变量 ABC+ABC =AB(C+C)=AB ABCD+ABCD-ACD 逻辑函数化简的实质就是相邻最小项的合并
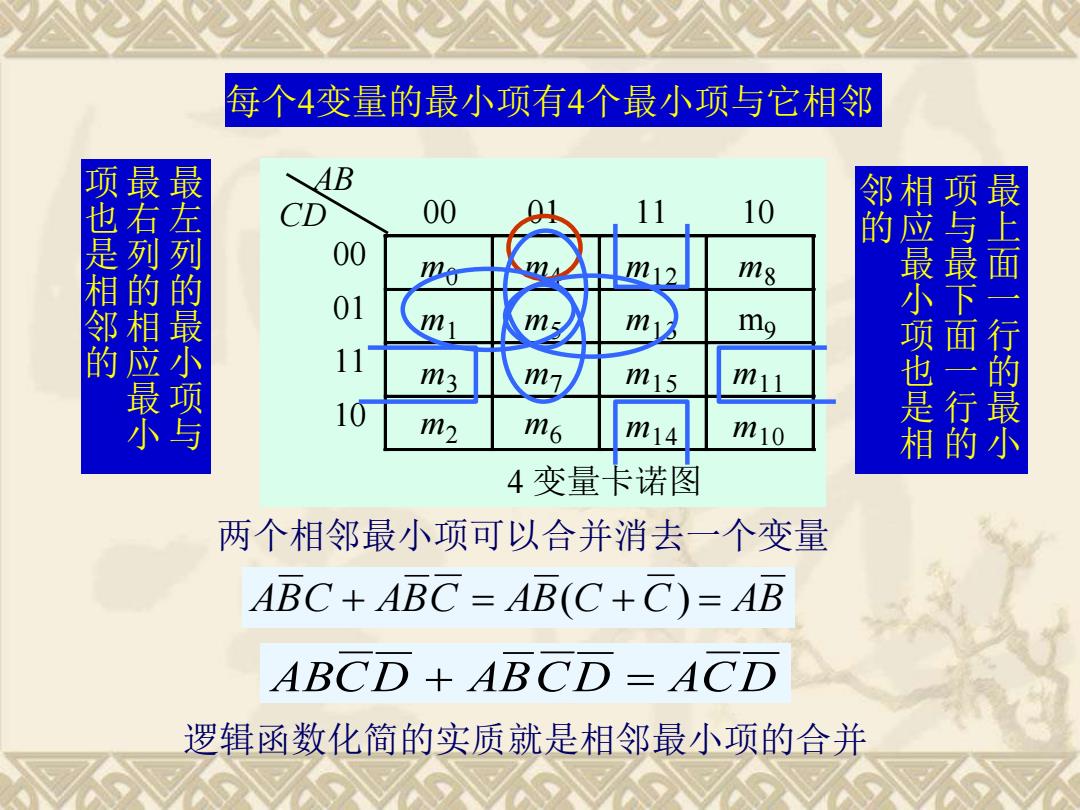
AB CD 00 01 11 10 00 m0 m4 m1 2 m8 01 m1 m5 m1 3 m9 11 m3 m7 m1 5 m11 10 m2 m6 m1 4 m10 4 变量卡诺图 每个4变量的最小项有4个最小项与它相邻 最 左 列 的 最 小 项 与 最 右 列 的 相 应 最 小 项 也 是 相 邻 的 最 上 面 一 行 的 最 小 项 与 最 下 面 一 行 的 相 应 最 小 项 也 是 相 邻 的 两个相邻最小项可以合并消去一个变量 ABC + ABC = AB(C + C) = AB ABCD + ABCD = ACD 逻辑函数化简的实质就是相邻最小项的合并

2、卡诺图构图思想: (1)n变量函数就有2n个小方格。每个小方格相当于 真值表中的一个最小项。小方格的编号就是最小项的编号。 (2)每个相邻小方格彼此只允许一个变量不同。通常采 用格雷码排列。保证逻辑相邻,几何位置相邻。 (3) 卡诺图小方格相邻数=变量数
(3) 卡诺图小方格相邻数 = 变量数。 (2) 每个相邻小方格彼此只允许一个变量不同。通常采 用格雷码排列。保证逻辑相邻,几何位置相邻。 2、卡诺图构图思想: (1) n 变量函数就有 2 n 个小方格。每个小方格相当于 真值表中的一个最小项。小方格的编号就是最小项的编号
1变量卡诺图 变量数n=1在卡诺图上有21=2个 小方格,对应mo、m两个最小项。 1 0表示A的反变量。 AB AB mo m 1表示A的原变量。 A AB AB 2变量卡诺图 mo m, 变量数n=2在卡诺图上有22=4个小方格,对应 m0、m1、m2、m3四个最小项。 每个小方格有二个相邻格:m0和m1、m2相邻 B 二变量格雷码排列: 任何相邻码组之间只有一个码元不同。 逻辑相邻,几何位置相邻
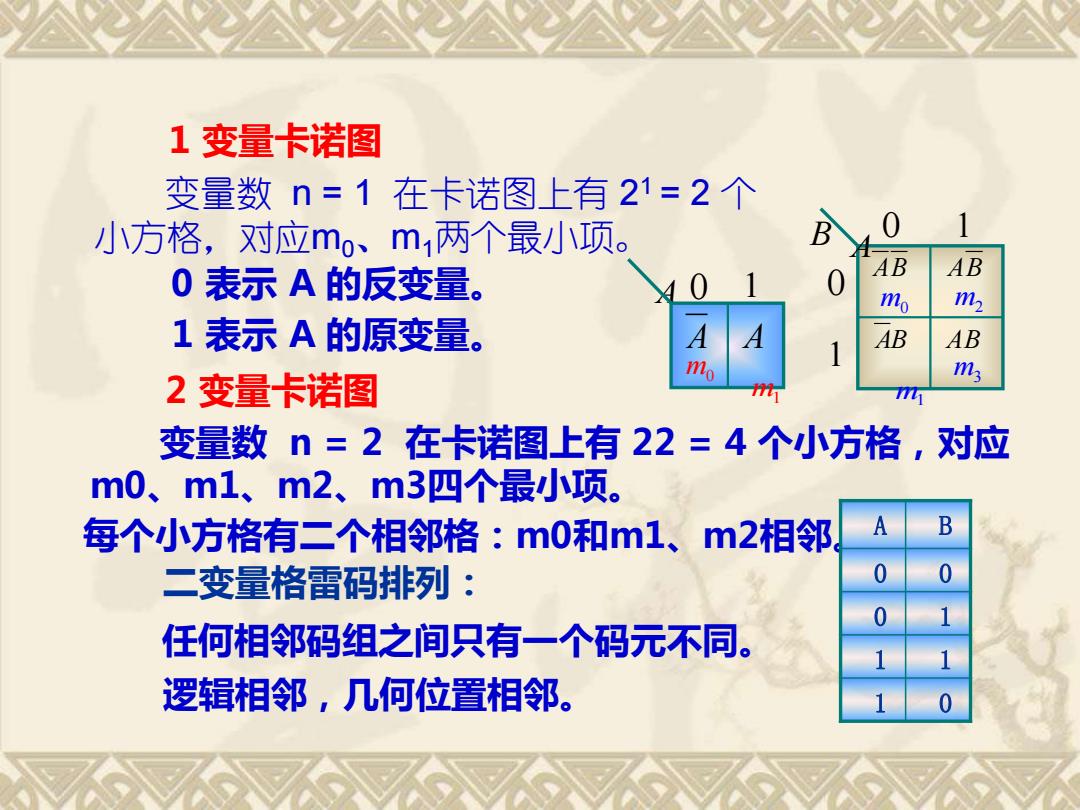
1 变量卡诺图 变量数 n = 1 在卡诺图上有 2 1 = 2 个 小方格,对应m0、m1两个最小项。 0 表示 A 的反变量。 1 表示 A 的原变量。 2 变量卡诺图 变量数 n = 2 在卡诺图上有 22 = 4 个小方格,对应 m0、m1、m2、m3四个最小项。 每个小方格有二个相邻格:m0和m1、m2相邻。A B 0 0 0 1 1 1 1 0 二变量格雷码排列: 任何相邻码组之间只有一个码元不同。 逻辑相邻,几何位置相邻。 A B AB AB AB AB m1 m0 m2 m3 0 1 0 1 A 0 1 m0 m1 A A

3变量卡诺图 AB 00 01 11 19 变量数n=3在卡诺图上 ABC ABC AB 有23=8个小方格,对应八个最 7l6 m A m 每个小方格有三个相邻格。 ABC ABC AB① AB 17 m mo和m1、m2、m4相邻。 m1和mo、m3、m5相邻。 m2和m0、m3、m6相邻。 ☆ 小方格的编号就是最小项的编号。 ☆ 卡诺图小方格相邻数=变量数。 ☆ 逻辑相邻,几何位置也相邻。 三变量格雷码排列顺序: 要求掌握格雷码排列规律
AB C 00 01 11 10 1 0 ABC ABC ABC ABC ABC ABC ABC ABC m0 m2 m1 m3 m4 m5 m6 m7 A B C 0 0 0 0 0 1 0 1 1 0 1 0 1 1 0 1 1 1 1 0 1 1 0 0 3 变量卡诺图 变量数 n = 3 在卡诺图上 有 2 3 = 8 个小方格,对应八个最。 每个小方格有三个相邻格。 m0 和m1、m2、m4 相邻。 m1 和m0、m3、m5 相邻。 m2 和m0、m3、m6 相邻。 三变量格雷码排列顺序: ☆ 卡诺图小方格相邻数 = 变量数。 ☆ 小方格的编号就是最小项的编号。 ☆ 逻辑相邻,几何位置也相邻。 要求掌握格雷码排列规律

4变量卡诺图 AB A A 变量数n=4在卡诺图上有 CD 24=16个小方格,对应十六个 BCD ABCD BCDABC 加 最小项。每个小方格有四个相邻 BCD 格 Q1 ABCD.ABCD ABCI 2 11 m 01。 0和m1、m2、m4、mg相邻。 ABCD ABCD ABCD ABCD m m5和m1、m4、m7、m13相邻。 0 BCD BC D ABCD mg和m1、m8、m11、m13相邻。 四变量格雷码排列: B A B
AB CD 00 01 11 10 00011110 ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD m0 m1 m2 m3 m4 m5 m7 m6 m8 m9 m11 m10 m12 m13 m15 m14 4 变量卡诺图 变量数 n = 4 在卡诺图上有 24 = 16 个小方格,对应十六个 最小项。每个小方格有四个相邻 格。 m0 和m1、m2、m4 、m8 相邻。 m5 和m1、m4、m7 、m13 相邻。 m9 和m1、m8、m11 、m13 相邻。 四变量格雷码排列: A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 B 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 C 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 D 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 A A C C B B D D
5变量卡诺图 ABC 000 001 011 010 110 DE 101 100 变量数n=5在卡诺图 00 mo 12 1m12 m s 1m24 1m28 m 20 m 16 上有25=32个小方格,对 01 m ms 1m5 ms 1m25 11机29 11机2i 1机7 应32个最小项。每个小方格 有5个相邻格。 1m3 m z 1m5 m i 1l27 13 1m23 1m19 10 m 1m6 mi4 m 10 11m26 1m30 1m22 m和m1、m2、m4、mg、及对称相m16 m5和m1、m4、m7、m13、及对称相m21o 找相邻格的方法 先按四变找 m23和m19、m21、m22、m31、及对称相m70 再找对称相 m27和m25、m26、m19、m31、及对称相m110 随着输入变量的增加,小方格数以2n倍增加。若 N=6有64个)小方格,使卡诺图变得十分复杂,相邻关系 难以寻找。所以卡诺图一般多用于5变量以内
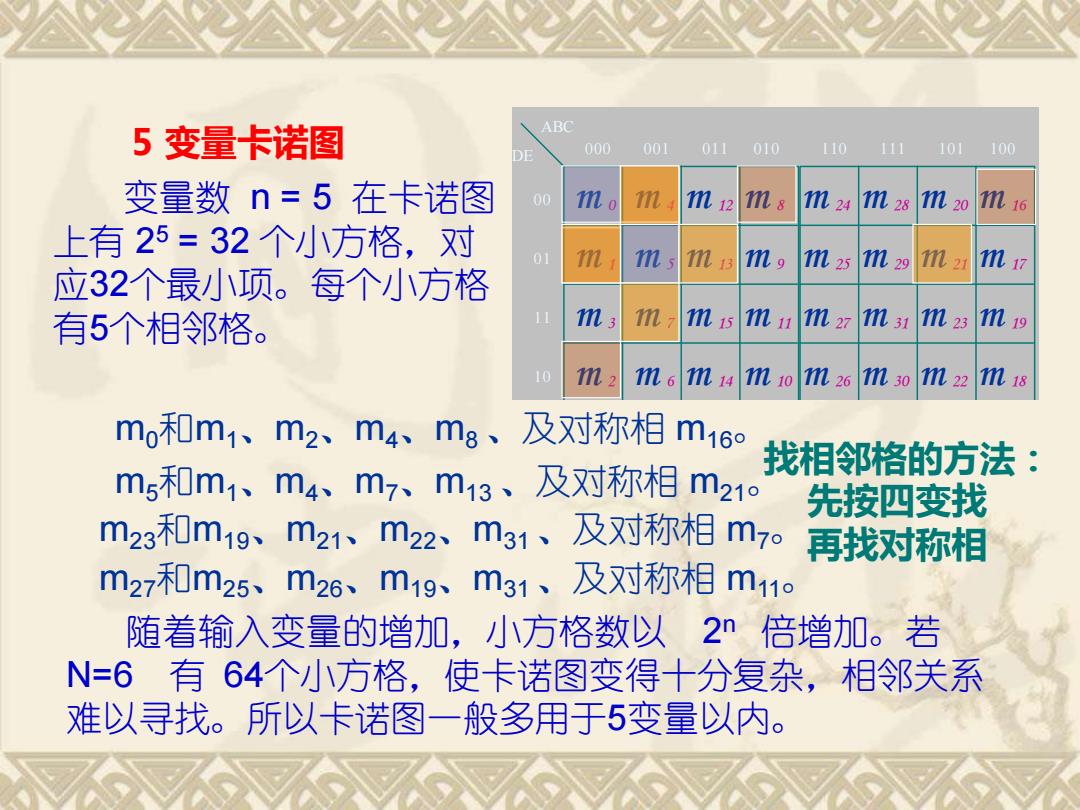
000 001 011 010 0 0 0 1 1 1 1 0 ABC DE 110 111 101 100 m 0 m 1 m 4 m 5 m 12 m 13 m 8 m 9 m 24 m 25 m 28 m 29 m 7 m 15 m 11 m 27 m 31 m 20 m 16 m 21 m 17 m 23 m 19 m 6 m 14 m 10 m 26 m 30 m 22 m 18 m 3 m 2 5 变量卡诺图 变量数 n = 5 在卡诺图 上有 2 5 = 32 个小方格,对 应32个最小项。每个小方格 有5个相邻格。 m0和m1、m2、m4、m8 、及对称相 m16。 m5和m1、m4、m7、m13 、及对称相 m21。 m23和m19、m21、m22、m31 、及对称相 m7。 m27和m25、m26、m19、m31 、及对称相 m11。 找相邻格的方法: 先按四变找 再找对称相 随着输入变量的增加,小方格数以 2 n 倍增加。若 N=6 有 64个小方格,使卡诺图变得十分复杂,相邻关系 难以寻找。所以卡诺图一般多用于5变量以内
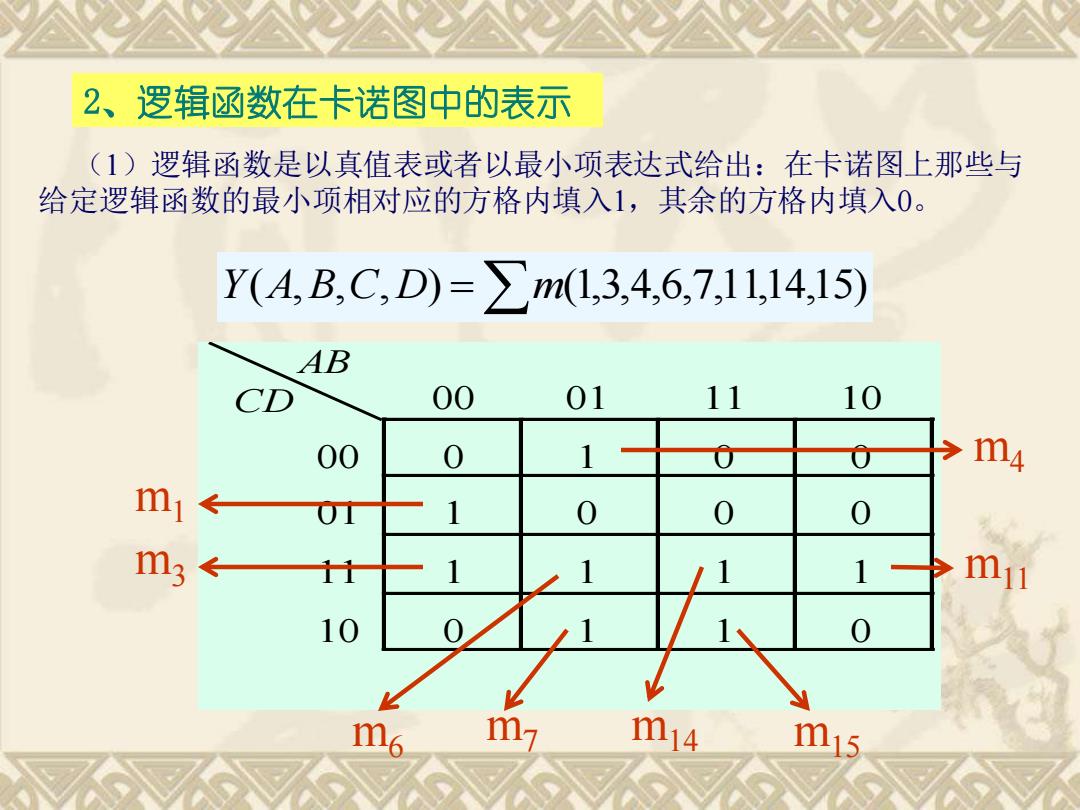
2、逻辑函数在卡诺图中的表示 (1)逻辑函数是以真值表或者以最小项表达式给出:在卡诺图上那些与 给定逻辑函数的最小项相对应的方格内填入1,其余的方格内填入0。 Y(A,B,C,D)=>m(1,3,4,6,7,11,14,15) AB CD 00 01 11 10 00 1 m4 mi 0 0 0 m3 m11 10 m7 m14 m15
2、逻辑函数在卡诺图中的表示 (1)逻辑函数是以真值表或者以最小项表达式给出:在卡诺图上那些与 给定逻辑函数的最小项相对应的方格内填入1,其余的方格内填入0。 AB CD 00 01 11 10 00 0 1 0 0 01 1 0 0 0 11 1 1 1 1 10 0 1 1 0 Y(A,B,C,D) =m(1,3,4,6,7,11,14,15) m1 m3 m4 m6 m7 m11 m14 m15

(2)逻辑函数以一般的逻辑表达式给出:先将函数变换为与或表达式(不 必变换为最小项之和的形式),然后在卡诺图上与每一个乘积项所包含的那 些最小项(该乘积项就是这些最小项的公因子)相对应的方格内填入1,其余 的方格内填入0。 Y=(A+D)(B+C) AD的公因子 圉 AB CD 11 10 00 Y=AD +BC 01 说明:如果求得了 110 函数Y的反函数Y,则 对Y中所包含的各个最 小项,在卡诺图相应方 格内填入0,其余方格内 BC的公因子 填入1
(2)逻辑函数以一般的逻辑表达式给出:先将函数变换为与或表达式(不 必变换为最小项之和的形式),然后在卡诺图上与每一个乘积项所包含的那 些最小项(该乘积项就是这些最小项的公因子)相对应的方格内填入1,其余 的方格内填入0。 Y = (A + D)(B + C) Y = AD + BC AB CD 00 01 11 10 00 1 1 0 0 01 0 0 0 0 11 1 0 0 1 10 1 1 0 1 变 换 为 与 或 表 达 式 AD的公因子 BC的公因子 说明:如果求得了 函数Y的反函数Y,则 对Y中所包含的各个最 小项,在卡诺图相应方 格内填入0,其余方格内 填入1