
第4章组合逻辑电路
第4章 组合逻辑电路

数字电路按逻辑功能的不同特点,可分为两大类, 一类称为组合逻辑电路,简称组合电路。另一类 称为时序逻辑电路,简称时序电路。 组合电路的特点是电路任意时刻输出状态,只取 决于该时刻的输入状态。而与该时刻前的电路输 入状态无关。 因为组合电路的特点所致,电路不需要包含有记 忆性的器件。所以组合电路中由各种门电路构成
❖ 数字电路按逻辑功能的不同特点,可分为两大类, 一类称为组合逻辑电路,简称组合电路。另一类 称为时序逻辑电路,简称时序电路。 ❖ 组合电路的特点是电路任意时刻输出状态,只取 决于该时刻的输入状态,而与该时刻前的电路输 入状态无关。 ❖ 因为组合电路的特点所致,电路不需要包含有记 忆性的器件。所以组合电路中由各种门电路构成

本章重点介绍组合逻辑电路的特点、以及组合电路的 分析方法和设计方法。 首先介绍组合逻辑电路的共同特点和一般分析方法及 设计方法。然后介绍常用的各种中规模集成电路的组合逻 辑电路的工作原理和使用方法。 最后从物理概念上说明竞争一冒险现象及其形成原因 并简单介绍消除竞争一冒险现象的常用方法。 常用组合电路有:全加器、译码器、 编码器、多路选 择器、多路分配器、 数值比较器、奇偶检验电路等。这些 组合电路经常使用,因此,均有中规模集成组件产品
本章重点介绍组合逻辑电路的特点、以及组合电路的 分析方法和设计方法。 首先介绍组合逻辑电路的共同特点和一般分析方法及 设计方法。然后介绍常用的各种中规模集成电路的组合逻 辑电路的工作原理和使用方法。 最后从物理概念上说明竞争-冒险现象及其形成原因, 并简单介绍消除竞争-冒险现象的常用方法。 常用组合电路有:全加器、译码器、编码器、多路选 择器、多路分配器、数值比较器、奇偶检验电路等。这些 组合电路经常使用,因此,均有中规模集成组件产品
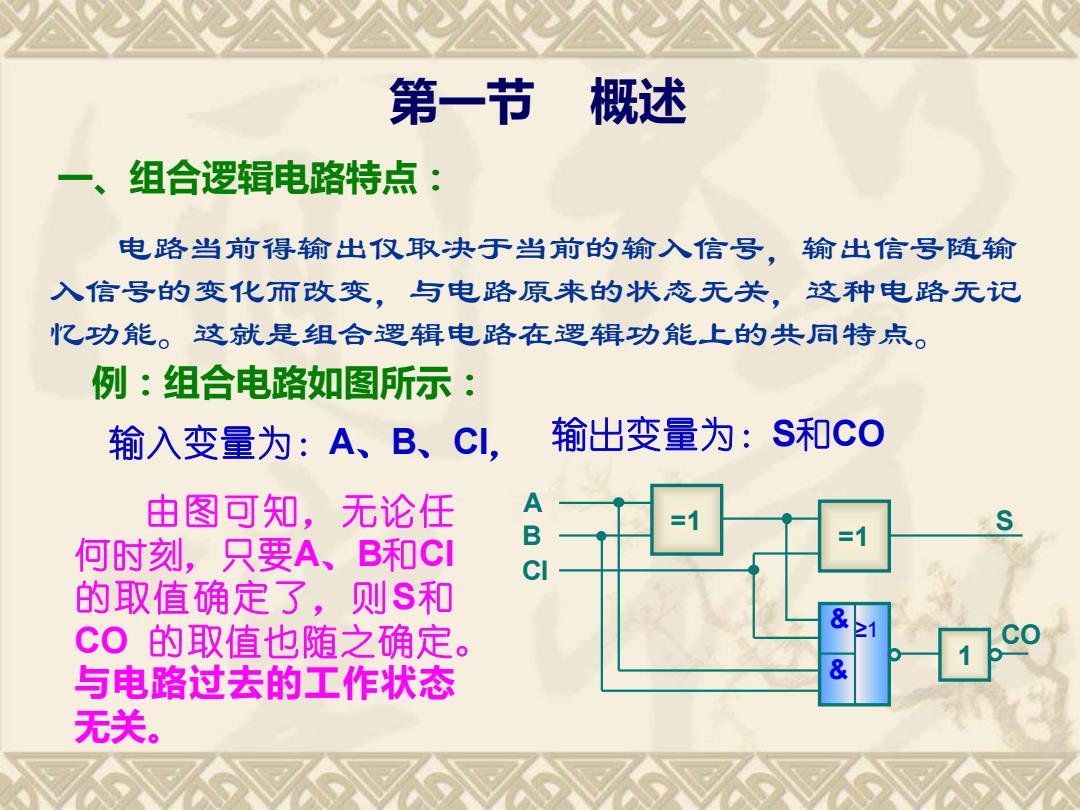
第一节 概述 一、组合逻辑电路特点 电路当前得输出仅取决于当前的输入信号,输出信号随输 入信号的变化而改变,与电路原来的状态无关, 这种电路无记 忆功能。这就是组合逻辑电路在逻辑功能上的共同特点。 例:组合电路如图所示: 输入变量为:A、B、Cl, 输出变量为:S和CO 由图可知,无论任 A B =1 何时刻,只要A、B和CI ci 的取值确定了,则$和 & CO的取值也随之确定。 与电路过去的工作状态 无关
一、组合逻辑电路特点: 电路当前得输出仅取决于当前的输入信号,输出信号随输 入信号的变化而改变,与电路原来的状态无关,这种电路无记 忆功能。这就是组合逻辑电路在逻辑功能上的共同特点。 例:组合电路如图所示: 输入变量为:A、B、CI, 输出变量为:S和CO 由图可知,无论任 何时刻,只要A、B和CI 的取值确定了,则S和 CO 的取值也随之确定。 与电路过去的工作状态 无关。 CO =1 =1 & & ≥1 1 A B CI S 第一节 概述

对于任何一个多输入、多输出的组合逻辑电路都可以 用一个框图来表示。 a y a1a2…an表示输入变量, 组合逻辑 y2 y1y2…ym表示输出变量。 电路 a m 输出与输入之间的逻辑关系可以用一组函数表示: y1=f(aa2、an) 组合电路逻辑功能特点 y2=f2(a个a2an) 是:输出只取决于当前输入状 态,与电路过去状态无关。所 yim=fm(aa2.…、an) 以,组合电路中,不包含有存 储单元。这就是组合电路在电 或者写成向量函数的形式: 路结构上的共同特点。 Y=F(A)
对于任何一个多输入、多输出的组合逻辑电路都可以 用一个框图来表示。 组合逻辑 电路 a1 a2 n a 1 y 2 y m y 1 2 n a 、a 、 a 表示输入变量, 1 2 m y 、y 、 y 表示输出变量。 输出与输入之间的逻辑关系可以用一组函数表示: ) 1 1 1 2 n y = f(a、a 、、a ) 2 2 a1 a2 an y = f( 、 、、 ) m m a1 a2 an y = f( 、 、、 或者写成向量函数的形式: Y = F(A) 组合电路逻辑功能特点 是:输出只取决于当前输入状 态,与电路过去状态无关。所 以,组合电路中,不包含有存 储单元。这就是组合电路在电 路结构上的共同特点

第二节 组合逻辑电路的分析和设计 4.2.1 组合逻辑电路的分析 从给定组合逻辑电路图找出输出和输入之间的逻辑关 系,分析其逻辑功能。 组合电路分析步骤: (1)根据给定逻辑电路图,从电路的输入到输出逐级写 出输出变量对应输入变量的逻辑表达式。 (2)由写出的逻辑逻辑表达式,列出真值表。 (3)从逻辑表达式或真值表.分析出组合逻辑电路的 逻辑功能
从给定组合逻辑电路图找出输出和输入之间的逻辑关 系,分析其逻辑功能. 组合电路分析步骤: (1)根据给定逻辑电路图,从电路的输入到输出逐级写 出输出变量对应输入变量的逻辑表达式。 (2)由写出的逻辑逻辑表达式,列出真值表。 (3)从逻辑表达式或真值表.分析出组合逻辑电路的 逻辑功能。 第二节 组合逻辑电路的分析和设计 4.2.1 组合逻辑电路的分析
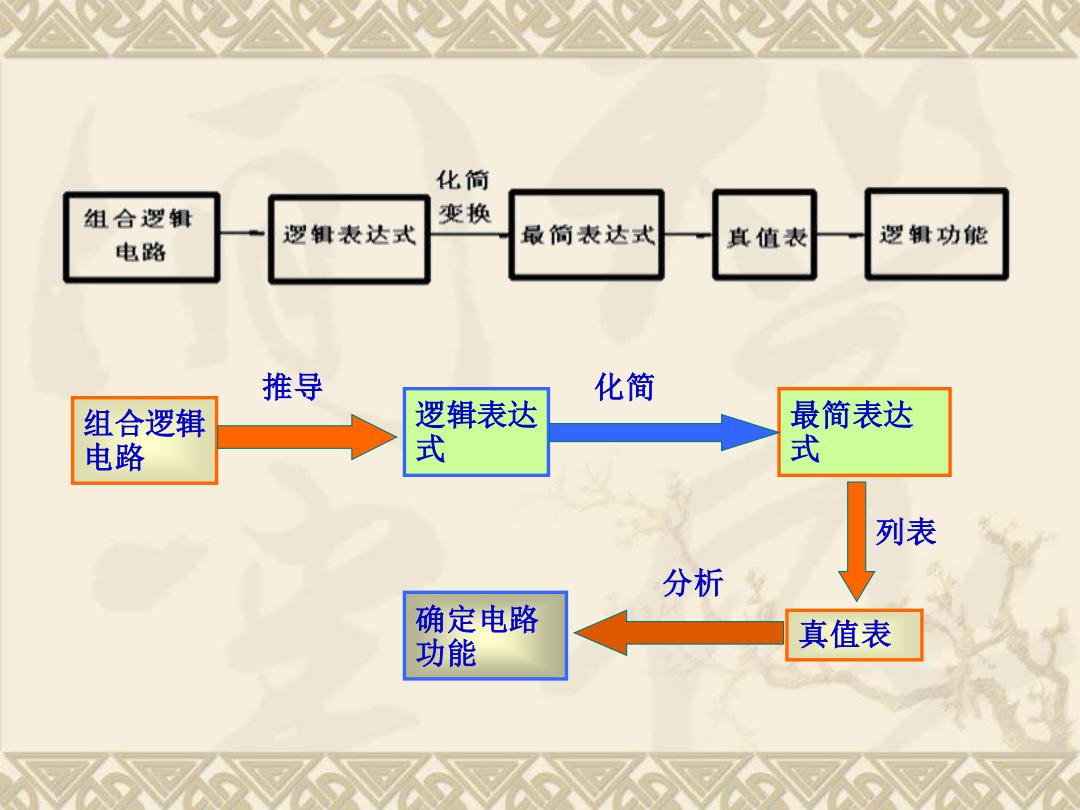
化简 组合逻辑 变换 逻辑表达式 最简表达式 逻辑功能 电路 其值表 推导 化简 组合逻辑 逻辑表达 简表达 电路 式 式 列表 分析 确定电路 功能 真值表
组合逻辑 电路 逻辑表达 式 最简表达 式 确定电路 真值表 功能 推导 化简 列表 分析
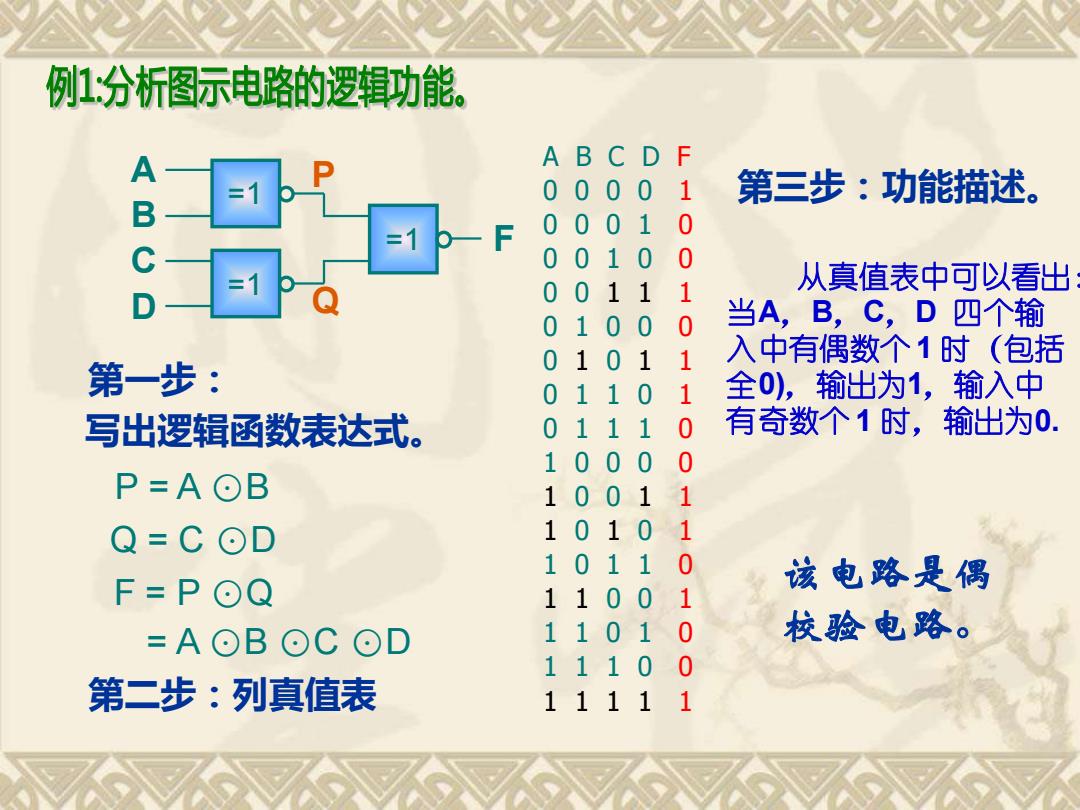
例1:分析图示电路的逻辑功能。 A AB C D F 0000 1 第三步:功能描述。 B 0001 0 0010 0 1 从真值表中可以看出 D 0011 0100 0 当A,B,C,D四个输 入中有偶数个1时(包括 第一步: 0101 1 0110 1 全0),输出为1,输入中 写出逻辑函数表达式。 0111 0 有奇数个1时,输出为0. 1000 0 P=A⊙B 1001 1 Q=C⊙D 10101 1011 0 F=P⊙Q 该电路是偶 11001 =A⊙B⊙C⊙D 11010 校验电路。 1110 0 第二步:列真值表 11111
第一步: P = A ⊙B Q = C ⊙D F = P ⊙Q A B C D F 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 1 1 1 1 该电路是偶 校验电路。 第三步:功能描述。 从真值表中可以看出: 当A,B,C,D 四个输 入中有偶数个 1 时(包括 全0),输出为1,输入中 有奇数个 1 时,输出为0. 第二步:列真值表 写出逻辑函数表达式。 = A ⊙B ⊙C ⊙D =1 =1 =1 A B C D F P Q
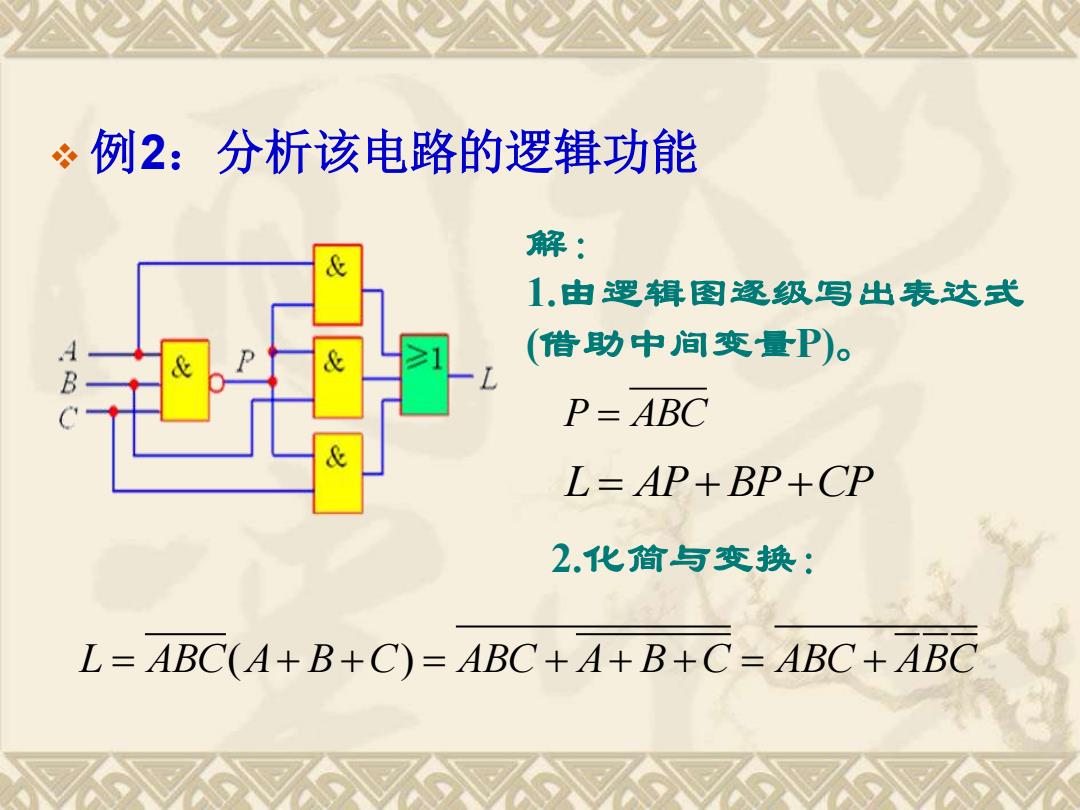
。例2:分析该电路的逻辑功能 解 & 1.由逻辑图逐级写出表达式 (借助中间变量P)。 P=ABC L=AP+BP+CP 2.化简与变换: L=ABC(A+B+C)=ABC+4+B+C=ABC+ABC
❖ 例2:分析该电路的逻辑功能 P ABC = L AP BP CP = + + L ABC A B C ABC A B C ABC ABC = + + = + + + = + ( ) 解: 1.由逻辑图逐级写出表达式 (借助中间变量P)。 2.化简与变换:

真值表 3.由表达式列出真值表。 A BC L 000 0 001 1 《4.分析逻辑功能: 010 1 当A、B、C三个变量不一 011 1 致时,输出为《1”,所以这个 100 1 电路称为“不一致电路”。 101 1 110 1 111 0
❖ 3.由表达式列出真值表。 ❖ 4.分析逻辑功能 : 当A、B、C三个变量不一 致时,输出为“1”,所以这个 电路称为“不一致电路