
第二章基本概念与基础知识
第二章 基本概念与基础知识

内容提要 信源(Information Source) 冬二进制与多进制 冬确定信号与随机信号 冬能量信号与功率信号 。频谱密度 基带与带通 冬带宽问题
内容提要 信源(Information Source) 二进制与多进制 确定信号与随机信号 能量信号与功率信号 频谱密度 基带与带通 带宽问题

通信术语 信源(Information Source) 模拟:An analogue signal is defined as a physical time varying quantity and is usually smooth and continuous, e.g.acoustic pressure variation when speaking.The performance of an analogue communications system is often specified in terms of its fidelity or quality,hence the term HIFI-HIgh FIdelity. ■ 数字:A digital signal on the other hand is made up of discrete symbols selected from a finite set,e.g.letters from the alphabet or binary data.The performance of a T digital system is specified in terms of accuracy of transmission e.g.Bit Error Rate (BER)and Symbol Error Rate (SER)
通信术语 信源(Information Source) 模拟:An analogue signal is defined as a physical time varying quantity and is usually smooth and continuous, e.g. acoustic pressure variation when speaking. The performance of an analogue communications system is often specified in terms of its fidelity or quality, hence the term HIFI – HIgh FIdelity. 数字:A digital signal on the other hand is made up of discrete symbols selected from a finite set, e.g. letters from the alphabet or binary data. The performance of a digital system is specified in terms of accuracy of transmission e.g. Bit Error Rate (BER) and Symbol Error Rate (SER)

二进制与多进制 冬二进制: ■比特(bit),为0,1;信息(数据)速率的单位bps 。多进制 ■码元或信元(symbol),为0,1,..,M-1;码元速率的单位:波特 (baud) 例如:当是四进制时,信元集合为{0,1,2,3},每个信元可以用二进制 表示成2bit,如0一00,1一01,2一10,3一11。当是M进制时(M一 般是2的n次方),包含了log2M个bit。 单位时间内传输一个二进制信元(即1个bit),数据传输速率就是 1bps;单位时间内传输一个M进制信元(相当于传输了1og2M个bit), 信元速率为1baud,数据传输速率为log2Mbps
二进制与多进制 二进制: 比特(bit),为0,1;信息(数据)速率的单位bps 多进制 码元或信元(symbol),为0,1,…,M-1;码元速率的单位:波特 (baud) 例如:当是四进制时,信元集合为{0,1,2,3},每个信元可以用二进制 表示成2bit,如0-00,1-01,2-10,3-11。当是M进制时(M一 般是2的n次方),包含了log2M个bit。 单位时间内传输一个二进制信元(即1个bit),数据传输速率就是 1bps;单位时间内传输一个M进制信元(相当于传输了log2M个bit), 信元速率为1baud,数据传输速率为log2M bps

确定信号与随机信号 冬确定信号:可以用明确的数学公式表示出来,在任何时间 的值都是确定已知的; 。随机信号:无法用一个明确的数学公式进行表示,在信号 实际发生前,值是不确定的。 通信系统中,需要处理的对象很多都是随机信号,因此 《概率论》和《随机过程》这两门课是通信信号处理的基 础,当然处理对象不同,还需要掌握其他知识,比如《矩 阵论》等
确定信号与随机信号 确定信号:可以用明确的数学公式表示出来,在任何时间 的值都是确定已知的; 随机信号:无法用一个明确的数学公式进行表示,在信号 实际发生前,值是不确定的。 通信系统中,需要处理的对象很多都是随机信号,因此 《概率论》和《随机过程》这两门课是通信信号处理的基 础,当然处理对象不同,还需要掌握其他知识,比如《矩 阵论》等

能量信号与功率信号 电信号可以用瞬时功率p()表示, p(t)=v2(t)/R p()=i2(t)R ■其中v()和()分别是流过电阻的电压和电流。 ·归一化后可统一表示成p()=x2() 在时间间隔(-T,T2》内的能量为E=小r(h 平均功率为:P= T 当且仅当信号在所有时间上的能量不为零且有限(0<E<∞)时,该 信号为能量信号;其中 E,=m2rut=小x(eh 当且仅当信号的平均功率不为零且有限(0<P<∞)时,该信号为功 率信号;其中 B=把7arua
能量信号与功率信号 电信号可以用瞬时功率p(t)表示, p(t)=v2 (t)/R p(t)=i2 (t)R 其中v(t)和i(t)分别是流过电阻的电压和电流。 归一化后可统一表示成p(t)=x2 (t) 在时间间隔(-T/2,T/2)内的能量为 平均功率为: 当且仅当信号在所有时间上的能量不为零且有限(0<Ex <∞)时,该 信号为能量信号;其中 当且仅当信号的平均功率不为零且有限(0<Px <∞)时,该信号为功 率信号;其中 / 2 2 / 2 ( ) T T x T E x t dt T T x x E P T / 2 2 2 / 2 lim ( ) ( ) T x T T E x t dt x t dt / 2 2 / 2 1 lim ( ) T x T T P x t dt T

很显然,能量信号的能量有限而平均功率为0,功率信号的 平均功率有限而能量无穷大。 。我们一般将模拟信号归为功率信号,因为模拟波形的持续时 间为无限长,能量是无穷大的,不能用能量来描述该信号, 功率(能量传输速率)更有意义; 冬数字系统中,一般都是用码元间隔为Ts的波形来发送和接收 码元,每个码元的平均功率(在整个时间轴上取平均)为0, 所以功率不能用于描述数字信号。因此,对于数字信号应该 采用能在时间窗内度量信号的测度,即码元能量(功率在Ts 上的积分)更有意义。 一般来说,周期信号和随机信号是功率信号,非周期的确定 信号是能量信号
很显然,能量信号的能量有限而平均功率为0,功率信号的 平均功率有限而能量无穷大。 我们一般将模拟信号归为功率信号,因为模拟波形的持续时 间为无限长,能量是无穷大的,不能用能量来描述该信号, 功率(能量传输速率)更有意义; 数字系统中,一般都是用码元间隔为Ts的波形来发送和接收 码元,每个码元的平均功率(在整个时间轴上取平均)为0, 所以功率不能用于描述数字信号。因此,对于数字信号应该 采用能在时间窗内度量信号的测度,即码元能量(功率在Ts 上的积分)更有意义。 一般来说,周期信号和随机信号是功率信号,非周期的确定 信号是能量信号

频谱密度 频谱密度:信号的能量或功率在频域上的分布特性。 能量谱密度(ESD) 利用Parsevals定理,信号x()在时域和频域的能量表达式为: E.=∫x2(dt=X(f)f 其中X0是x(0的傅立叶变换,设平.f)=X(f乃则平(f)就是x的能 量谱密度。 冬功率谱密度(PSD) ■设x()是周期为T的周期信号(功率信号),则在信号周期T。上的平均功 率为: 1=-o0 其中c是周期信号傅立叶级数的复系数的幅值。 功率谱密度 G,(f)=∑c2δf-nf%)
频谱密度 频谱密度:信号的能量或功率在频域上的分布特性。 能量谱密度(ESD) 利用Parseval定理,信号x(t)在时域和频域的能量表达式为: 其中X(f)是x(t)的傅立叶变换,设 ,则 就是x(t)的能 量谱密度。 功率谱密度(PSD) 设x(t)是周期为T0的周期信号(功率信号),则在信号周期T0上的平均功 率为: 其中|cn |是周期信号傅立叶级数的复系数的幅值。 功率谱密度 2 2 ( ) ( ) E x t dt X f df x 2 ( ) ( ) x f X f ( ) x f 0 0 / 2 2 2 / 2 0 1 ( ) T x n T n P x t dt c T 2 0 ( ) ( ) x n n G f c f nf

G()的几个性质 1.G(①20,且为实数; 2.Gx(①=Gx(-f),对实值x): 3.Gx(⑤←→R(T),PSD与自相关函数是傅立叶变换对; 4.P=G,(f)f,归一化平均功率与PSD之间的关系。 研究平,(f)和G,(f)的目的,主要为研究信号能量或功 率在频域内的分布规律,以便合理地选择信号的通频带, 对传输电路提出恰当的频带要求,尽量做到在信号不失 真或失真不大的条件下提高信噪比
研究 和 的目的,主要为研究信号能量或功 率在频域内的分布规律,以便合理地选择信号的通频带, 对传输电路提出恰当的频带要求,尽量做到在信号不失 真或失真不大的条件下提高信噪比。 ( ) x f ( ) G f x 1. Gx (f) ≥0,且为实数; 2. Gx (f)=Gx (-f),对实值x(t); 3. Gx (f) Rx ( ) ,PSD与自相关函数是傅立叶变换对; ( ) P G f df x x 4. ,归一化平均功率与PSD之间的关系。 Gx (f)的几个性质
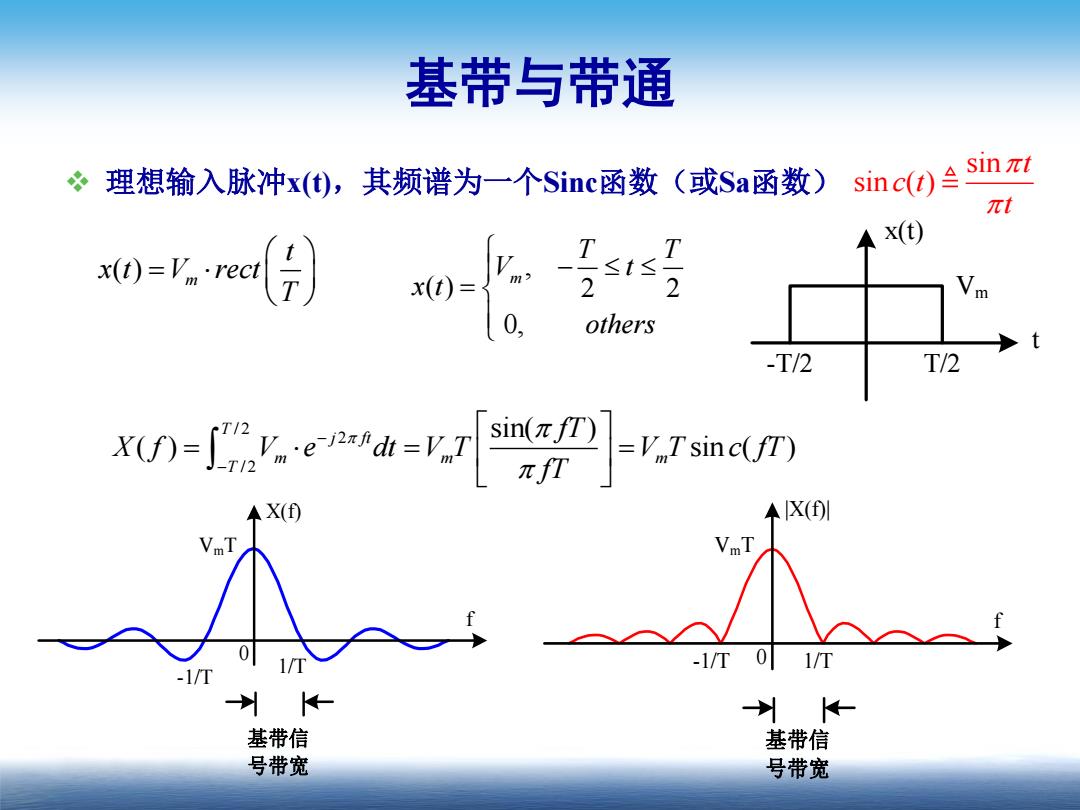
基带与带通 理想输入脉冲x(),其频谱为一个Sinc函数(或Sa函数)sinc(t)会 lnπt πt x(t) x(t)=Vrect 2 Vm 0, others -T/2 T/2 F.T sncUt) ◆X(f ◆X() VmT VmT 0 -1/T01/T 州← 基带信 基带信 号带宽 号带宽
基带与带通 理想输入脉冲x(t),其频谱为一个Sinc函数(或Sa函数) , ( ) 2 2 0, m T T V t x t others ( ) m t x t V rect T sin sin ( ) t c t t / 2 2 / 2 sin( ) ( ) sin ( ) T j ft m m m T fT X f V e dt V T V T c fT fT x(t) t -T/2 T/2 Vm VmT f X(f) 0 -1/T 1/T 基带信 号带宽 VmT f |X(f)| -1/T 0 1/T 基带信 号带宽