中国科学技术大学：《编码理论》课程教学资源（课件讲义）第九章 Polar码

第九章Polart码

第九章 Polar码

本章内容 冬Polar码简介 。信道极化 冬Polar码的编码 Polar码的译码

本章内容 Polar码简介 信道极化 Polar码的编码 Polar码的译码 2

Polar码简介 Polar码是由土耳其Bilkent大学教授Erdal Arikan于 2007年基于信道极化理论提出的一种线性信道编码方法 ，该码字是唯一能够从理论上达到香农限的编码方法，并 具有较低的编译码复杂度，当码长为N时，复杂度为 O(NlogN)。Polar码的核心思想就是信道极化理论， 不同的信道对应的极化方法也有区别

Polar码简介  Polar码是由土耳其Bilkent大学教授Erdal Arikan于 2007年基于信道极化理论提出的一种线性信道编码方法 ，该码字是唯一能够从理论上达到香农限的编码方法，并 具有较低的编译码复杂度，当码长为N时，复杂度为 O(NlogN)。Polar码的核心思想就是信道极化理论， 不同的信道对应的极化方法也有区别。 3

。Pola码的理论基础就是信道极化，它包括信道合并和信 道分解两部分。当合并信道的数目趋于无穷大时，则会出 现极化现象：一部分信道将趋于无噪信道，另外一部分则 趋于全噪信道，这种现象就是信道极化。无噪信道的传输 速率会达到信道容量I(W),而全噪信道的传输速率趋于 0。Poar码的编码策略正是应用了这种现象的特性，利 用无噪信道传输用户的有用信息，全噪信道传输约定的信 息或者不传信息。 基于信道极化理论提出的极化码，是第一类被证明在码长 无限长时、采用逐次消除译码算法可严格达到二元对称信 道容量的信道编码方案

 Polar码的理论基础就是信道极化，它包括信道合并和信 道分解两部分。当合并信道的数目趋于无穷大时，则会出 现极化现象：一部分信道将趋于无噪信道，另外一部分则 趋于全噪信道，这种现象就是信道极化。无噪信道的传输 速率会达到信道容量I(W)，而全噪信道的传输速率趋于 0。Polar码的编码策略正是应用了这种现象的特性，利 用无噪信道传输用户的有用信息，全噪信道传输约定的信 息或者不传信息。  基于信道极化理论提出的极化码，是第一类被证明在码长 无限长时、采用逐次消除译码算法可严格达到二元对称信 道容量的信道编码方案。 4

二进制离散无记忆信道(BDMC)有两个主要的信道参数：信道容量 和Bhattacharyya参数。 给定一个BDMC信道W:X→Y,X和Y为输入和输出，令P(YI)为 信道转移概率，其中X∈0,1}。对于信道W,信道容量I(W)和 Bhattacharyya参数Z(W)（简记为Z参数)分别为： 1w-Σoa P(y x) vEYx∈X 2PU1092PoID Z(W)=∑VPy10PyII) y∈V 这两个参数分别用于速率和可靠性的衡量。I(W)是等概信源通过信道 W可靠传输的最高速率。巴氏参数Z(W)是信道使用一次最大似然判 决错误概率的上限。I(W)和Z(W)的取值范围都为[0,1]，当 I(W)≈1时，Z(W)=0;Z(W)≈1时，I(W)=0

 给定一个BDMC信道W：XY，X和Y为输入和输出，令P(Y|X)为 信道转移概率，其中X∈{0,1}。对于信道W，信道容量I(W)和 Bhattacharyya参数Z(W)（简记为Z参数）分别为： 5 1 (|) ( ) ( | )log 2 1 1 ( | 0 ) ( |1) 2 2 y Yx X Py x IW Py x Py Py ∈ ∈ = + ∑∑ ( ) ( | 0 )( |1) y Y ZW Py Py ∈ = ∑  这两个参数分别用于速率和可靠性的衡量。I(W)是等概信源通过信道 W可靠传输的最高速率。巴氏参数Z(W)是信道使用一次最大似然判 决错误概率的上限。 I(W)和 Z(W)的取值范围都为[0,1]， 当 I(W)≈1时，Z(W)=0; Z(W)≈1时，I(W)=0。  二进制离散无记忆信道（BDMC）有两个主要的信道参数：信道容量 和Bhattacharyya参数

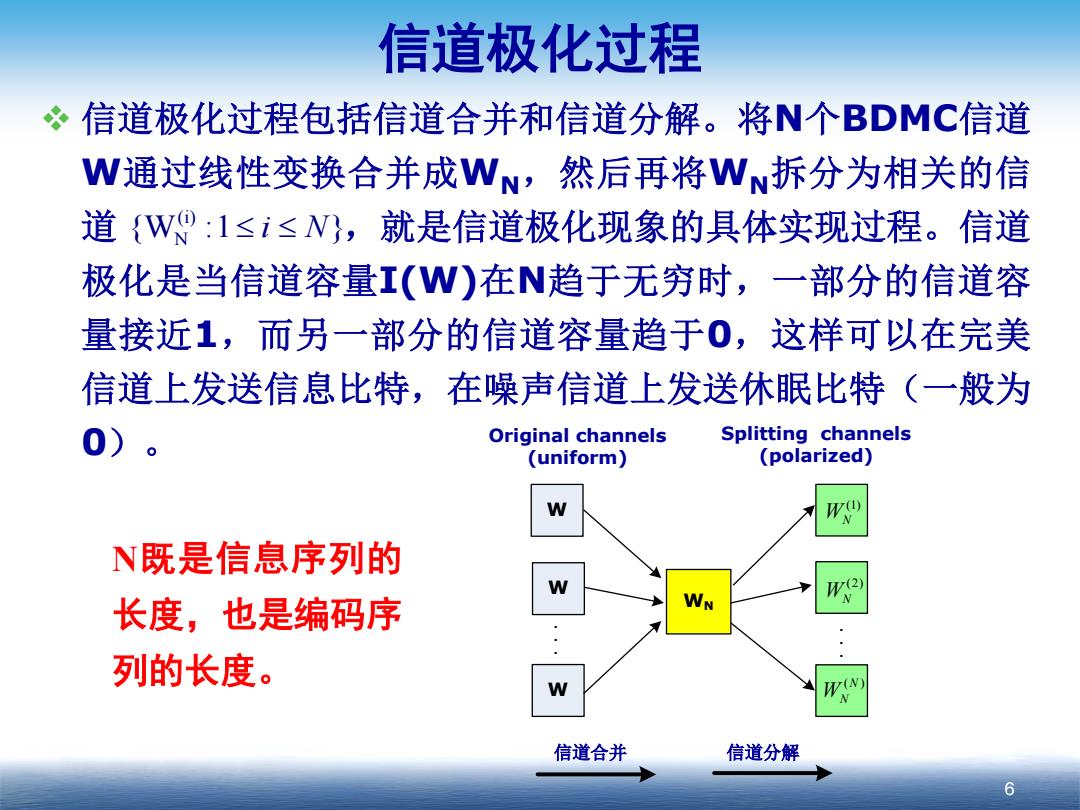
信道极化过程 信道极化过程包括信道合并和信道分解。将N个BDMC信道 W通过线性变换合并成WN,然后再将WN拆分为相关的信 道{W0:1≤i≤W,就是信道极化现象的具体实现过程。信道 极化是当信道容量I(W)在N趋于无穷时，一部分的信道容 量接近1，而另一部分的信道容量趋于0，这样可以在完美 信道上发送信息比特，在噪声信道上发送休眠比特（一般为 0) Original channels Splitting channels (uniform) (polarized) N既是信息序列的 长度，也是编码序 WN 列的长度。 (N 信道合并 信道分解 6

信道极化过程  信道极化过程包括信道合并和信道分解。将N个BDMC信道 W通过线性变换合并成WN，然后再将WN拆分为相关的信 道 ，就是信道极化现象的具体实现过程。信道 极化是当信道容量I(W)在N趋于无穷时，一部分的信道容 量接近1，而另一部分的信道容量趋于0，这样可以在完美 信道上发送信息比特，在噪声信道上发送休眠比特（一般为 0）。 6 (i) N {W :1 } ≤ ≤i N W W W WN (1) WN (2) WN ( ) N WN 信道合并 信道分解 Original channels (uniform) Splitting channels (polarized) . . . . . . N既是信息序列的 长度，也是编码序 列的长度

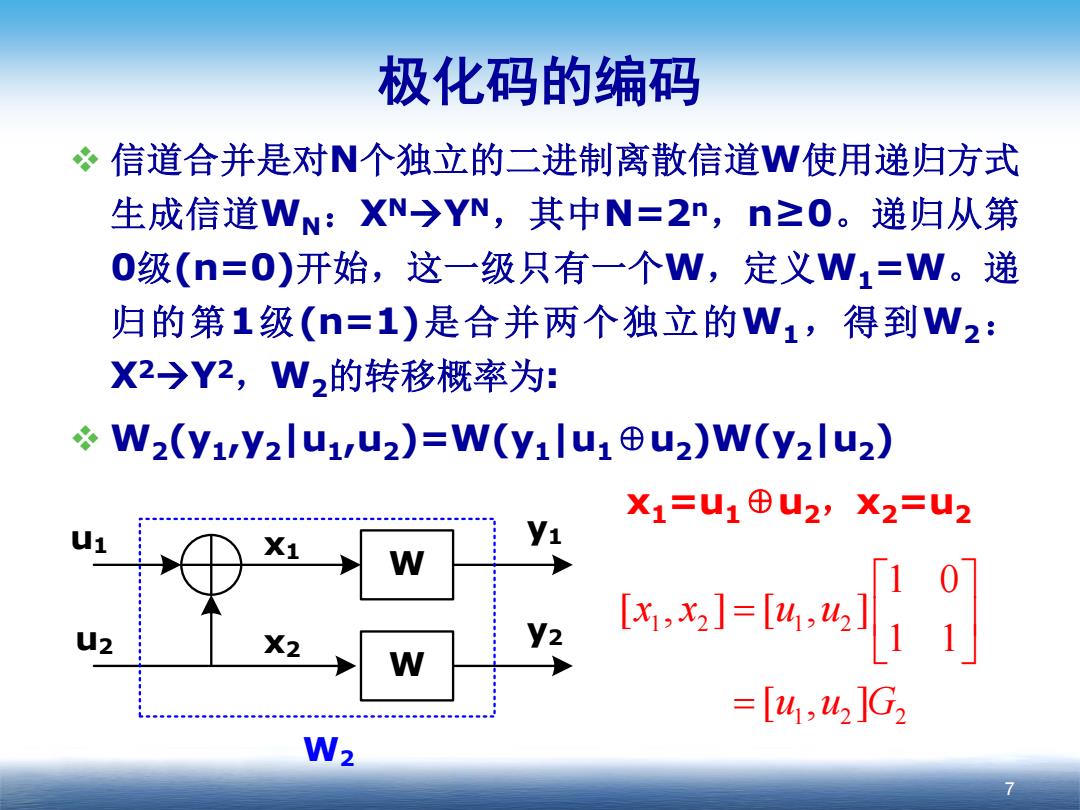
极化码的编码 信道合并是对N个独立的二进制离散信道W使用递归方式 生成信道WN:XN→YN,其中N=2n,n≥0。递归从第 0级(n=0)开始，这一级只有一个W,定义W1=W。递 归的第1级(n=1)是合并两个独立的W1,得到W2: X2→Y2,W2的转移概率为： *W2(y1y2lu1,u2)=W(yilu1u2)W(y2lu2) X1=U1⊕u2,X2=U2 X1 W 2 X2 kx1-eal0 W =[4,42]G2 W2

极化码的编码  信道合并是对N个独立的二进制离散信道W使用递归方式 生成信道WN：XNYN ，其中N=2n ，n≥0。递归从第 0级(n=0)开始，这一级只有一个W，定义W1=W。递 归的第1级(n=1)是合并两个独立的W1，得到W2： X2Y2 ，W2的转移概率为:  W2(y1,y2|u1,u2)=W(y1|u1⊕u2)W(y2|u2) x1=u1⊕u2，x2=u2 7 W u2 W u1 x1 x2 y1 y2 W2 12 12 12 2 1 0 [, ][, ] 1 1 [, ] xx uu uuG   =     =

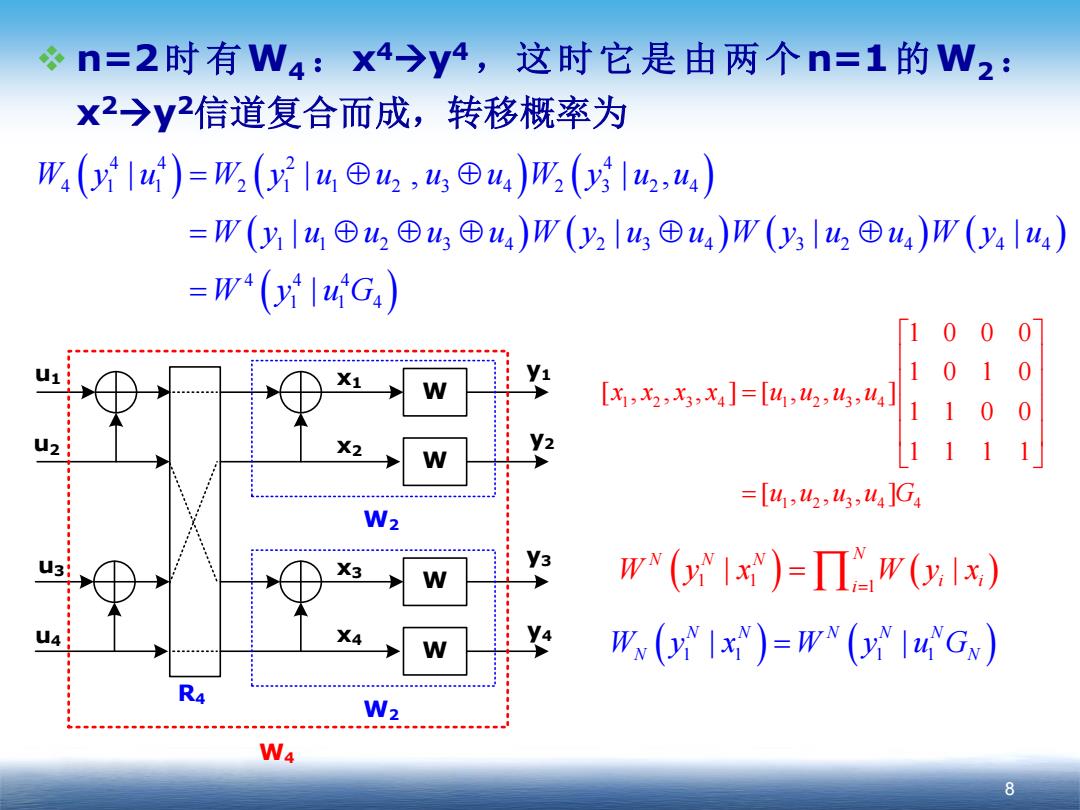
n=2时有W4:x4→y4,这时它是由两个n=1的W2: x2→y2信道复合而成，转移概率为 W,(14)=W(14⊕，⑧山4)m(g4,4） =W(y4⊕42⊕4⊕4)W(y2l4田u4)W(yl42田u4)W(y4lu4) =W4(y14G4) 100 0 10 1 0 X1 W [x1,X2,x3,x4]=[41,42,43,u4] 110 0 X2 W 111 =[41,42,43,u4]G4 W2 u3 y3 Wv(yIx)=ΠW(yx) 14 X4 W(（yIx)=W(yI4Gw) R4 W2 W4 8

 n=2时有W4：x4y4 ，这时它是由两个n=1的W2： x2y2信道复合而成，转移概率为 8 W u2 W u1 x1 x2 y1 y3 W2 W W x3 x4 W2 u3 u4 R4 y2 y4 W4 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 44 2 4 4 1 1 2 1 1 2 3 4 2 3 24 11 2 3 4 2 3 4 3 2 4 4 4 444 1 14 | | , | , | ||| | W y u W y u u u uW y uu Wyu u u uWy u uWy u uWy u W y uG = ⊕⊕ = ⊕⊕⊕ ⊕ ⊕ = 1234 1234 1234 4 1000 1010 [, , , ][, , , ] 1100 1111 [, , , ] xx x x uuuu uuuuG     =         = ( 1 1 ) ( ) 1 | | NNN N i i i W y x Wyx = =∏ ( 1 1 | | ) ( 1 1 ) NN NNN W y x W y uG N N =

如果把线拉直，则为下图所示 u1 X1 X2 y2 W W2 3到 X3 X W .. R4 W2 W4 uf X1 y1 W 1 0 U3 2 y2 W 1 0 1 u2 X3 y3 W 1 u4 X4 y4 W X 4 9

 如果把线拉直 ，则为下图所示 9 W u 2 W u 1 x 1 x 2 y 1 y 3 WW x 3 x 4 u 3 u 4 y 2 y 4 W u 2 W u 1 x 1 x 2 y 1 y 3 W 2 WW x 3 x 4 W 2 u 3 u 4 R 4 y 2 y 4 W 4 4 1000 1010 1100 1111 G     =         = G4 x u

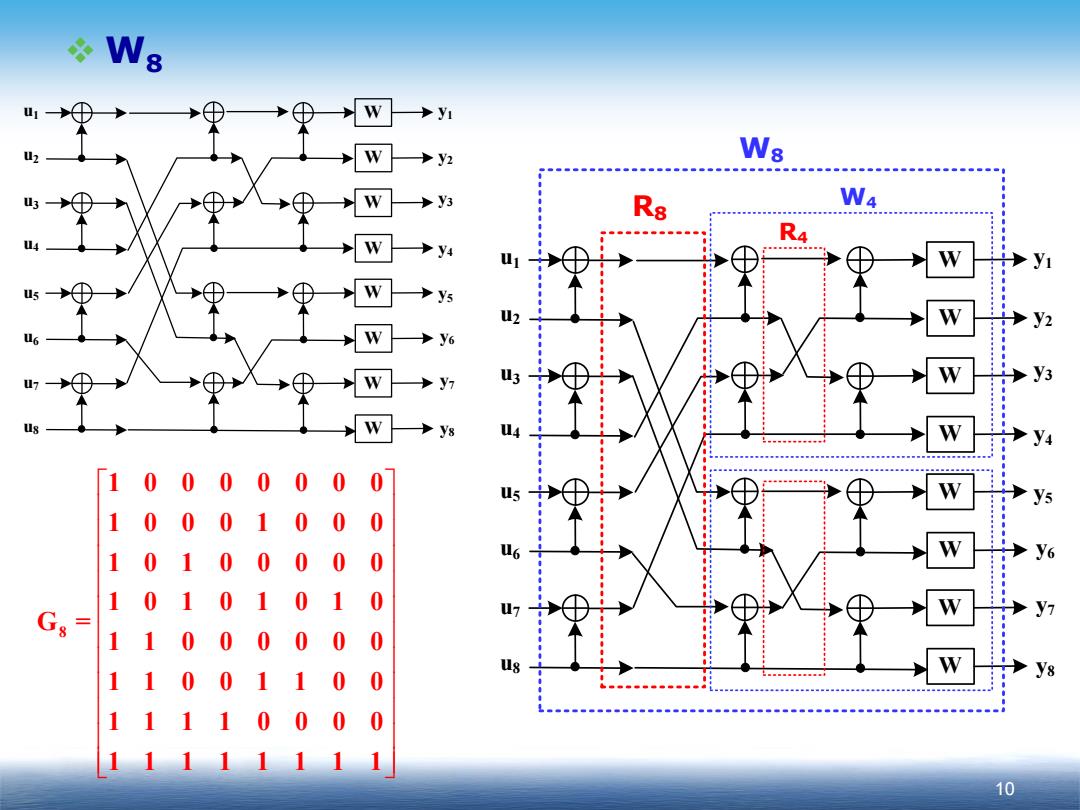
Ws y1 y2 Ws W y3 Ra W4 R4 y4 uj W W y5 2 y2 W y6 y7 山3 y3 W y8 y4 1000000 0 5 10 00100 0 10100 00 0 06 1010101 0 Gs y7 1 1 00000 0 1100110 ys 0 11110 00 0 11111 11 10

 W 8 10 u 2 u 1 y 1 u 3 y 3 u 4 y 2 y 4 u 7 u 5 u 6 u 8 y 5 y7 y6 y8 WWWWWWWW u 2 u 1 y 1 u 3 y 3 u 4 y 2 y 4 u 7 u 5 u 6 u 8 y 5 y7 y6 y8 WWWWWWWW R 8 R 4 W 4 W 8       8 10000000 10001000 10100000 10101010 G = 11 000000 11 0011 00 1111 0000 11111111