
第四章卷积码的编码 第四章卷积码 卷积码与分组码不同,其编码器具有记忆性,即编码器的当前输出不仅与当前输入有关, 还跟以前时刻的输入有关。速率R=kn、存储器阶数为m的卷积编码器可用k个输入、n个 输出、输入存储器阶数为m的线性序贯电路实现,即输入在进入编码器后仍会多呆m个时 间单元。通常,n和k都是比较小的整数,k<n,信息序列被分成长度为k的分组,码字(codeword) 被分成长度为的分组。当k=1时,信息序列无需分组,处理连续进行。值得注意的是, 卷积码不象分组码,较大的最小距离和低错误概率不是通过增加k和实现的,而是通过增 加存储器阶数m实现的。 我们这一章关注卷积编码过程、卷积编码器如何用状态图表示、如何推导卷积码的重量 枚举(weight--enumerating)函数、卷积码的几种距离测量方法。 卷积码是1955年由Elias(1923~2001)首次提出的,随后Wozencraft和Reiffen提出 了序贯译码方法(对具有较大约束长度的卷积码非常有效)。1963年,Massey提出了一个 效率不高、但易于实现的译码方法一一门限译码,这使得卷积码大量应用于卫星和无线信道 的数字传输中。 On December 7,2001,the field of information theory lost another of its true giants,Peter Elias, who passed away at his home in Cambridge, Massachusetts,a victim of the mysterious and dreadful ailment,Creutzfeld-Jakob Disease. Peter Elias AJ.Viterbi毕业于麻省理工学院(MT),分别获博士/硕士 /学士学位,是无线通信领域国际权威专家,被称为CDMA 之父。现为美国Qualcomm公司首席科学家,加州大学Los Angeles分校(UCLA)教授,IEEE Fellow(国际电子电气 工程师协会会士),美国总统国家科学和工程委员会成员。 I967年,Viterbi提出了最大似然(ML,Maximum Likelihood)译码算法,易于实现具 有较小约束长度的卷积码的软判决译码。Viterbi算法配合序贯译码的软判决,使卷积码在 20世纪70年代广泛应用在深空和卫星通信系统。1974年,Bahl,Cocke,Jelinek以及Raviv (BCJR)对具有不等先验概率信息比特的卷积码,提出了最大后验概率(MAP,maximum a posteriori probability)译码算法。BCJR算法近年来广泛应用到软判决迭代译码方案中,其 中信息比特的先验概率在每次迭代时都发生变化。对卷积码描述最详尽的书籍是: R.Johannesson and K.S.Zigangirov,Fundamentals of Convolutional Coding.IEEE Press,Piscataway,N.J.,1999. Copyright by周武旸
第四章 卷积码的编码 1 Copyright by 周武旸 第四章 卷积码 卷积码与分组码不同,其编码器具有记忆性,即编码器的当前输出不仅与当前输入有关, 还跟以前时刻的输入有关。速率 R=k/n、存储器阶数为 m 的卷积编码器可用 k 个输入、n 个 输出、输入存储器阶数为 m 的线性序贯电路实现,即输入在进入编码器后仍会多呆 m 个时 间单元。通常,n和k都是比较小的整数,k<n,信息序列被分成长度为k的分组,码字(codeword) 被分成长度为 n 的分组。当 k=1 时,信息序列无需分组,处理连续进行。值得注意的是, 卷积码不象分组码,较大的最小距离和低错误概率不是通过增加 k 和 n 实现的,而是通过增 加存储器阶数 m 实现的。 我们这一章关注卷积编码过程、卷积编码器如何用状态图表示、如何推导卷积码的重量 枚举(weight-enumerating)函数、卷积码的几种距离测量方法。 卷积码是 1955 年由 Elias(1923~2001)首次提出的,随后 Wozencraft 和 Reiffen 提出 了序贯译码方法(对具有较大约束长度的卷积码非常有效)。1963 年,Massey 提出了一个 效率不高、但易于实现的译码方法――门限译码,这使得卷积码大量应用于卫星和无线信道 的数字传输中。 1967 年,Viterbi 提出了最大似然(ML, Maximum Likelihood)译码算法,易于实现具 有较小约束长度的卷积码的软判决译码。Viterbi 算法配合序贯译码的软判决,使卷积码在 20 世纪 70 年代广泛应用在深空和卫星通信系统。1974 年,Bahl, Cocke, Jelinek 以及 Raviv (BCJR)针对 具有不等先验概率信息比特的卷积码,提出了最大后验概率(MAP,maximum a posteriori probability)译码算法。BCJR 算法近年来广泛应用到软判决迭代译码方案中,其 中信息比特的先验概率在每次迭代时都发生变化。对卷积码描述最详尽的书籍是: R. Johannesson and K.S. Zigangirov, Fundamentals of Convolutional Coding. IEEE Press, Piscataway , N. J., 1999. On December 7, 2001, the field of information theory lost another of its true giants, Peter Elias, who passed away at his home in Cambridge, Massachusetts, a victim of the mysterious and dreadful ailment, Creutzfeld-Jakob Disease. A.J.Viterbi 毕业于麻省理工学院(MIT),分别获博士/硕士 /学士学位,是无线通信领域国际权威专家,被称为 CDMA 之父。现为美国 Qualcomm 公司首席科学家,加州大学 Los Angeles 分校(UCLA)教授,IEEE Fellow(国际电子电气 工程师协会会士),美国总统国家科学和工程委员会成员

第四章卷积码的编码 4.1卷积码的编码 卷积码的编码分为两类:前馈和反馈,在每类中又可分为系统和非系统形式。首先考虑 非系统形式的前馈编码器。 例4.1速率R=1/2的非系统前馈卷积编码器 图4.1为速率R=1/2、存储器阶数m=3的非系统前馈卷积编码器框图,该编码器中输 入信息比特k=1、n=2个模2加法器、m=3个延时单元。由于模2加法器是一个线性运算, 因此编码器是一个线性系统,所有卷积码都可用这类线性前馈移位寄存器编码器实现。 图41速率R=1/2的非系统前馈卷积编码器 信息序列u=(4o,4,42,)进入编码器,每次1比特,由于编码器是一个线性系统,两 个编码器输出序列v0=(,,°,…)和v0=(,,”,…)可通过输入序列u和两 个编码器脉冲响应的卷积得到。计算脉冲响应时,可设=(100..),然后观测两个输出序 列。对一个具有m阶存储器的编码器,脉冲响应能够持续最多+1个时间单元,可写为 g)=(g60,g,g°,,g)和g=(g6,g",g,g)。对上图的编码器,有 g0=(1011) (4.1) g9=1111) 脉冲响应g和g称为编码器的生成器序列。这样,编码方程为: vo)=u⑧g (4.2) v"=u⑧g9 其中⑧表示离散卷积,且所有运算都是模2加运算,对于所有1≥0,有: 90-24-89 (4.3) =48+4-1g+…+4-mgR,j=0,1 其中对于所有<i,山兰0,这样对图4.1所示的编码器,有: 0=山 +41-2+4-3 (4.4) y0=4,+41+4-2+4- 2 Copyright by周武旸
第四章 卷积码的编码 2 Copyright by 周武旸 4.1 卷积码的编码 卷积码的编码分为两类:前馈和反馈,在每类中又可分为系统和非系统形式。首先考虑 非系统形式的前馈编码器。 ====================================== 例 4.1 速率 R=1/2 的非系统前馈卷积编码器 图 4.1 为速率 R=1/2、存储器阶数 m=3 的非系统前馈卷积编码器框图,该编码器中输 入信息比特 k=1、n=2 个模 2 加法器、m=3 个延时单元。由于模 2 加法器是一个线性运算, 因此编码器是一个线性系统,所有卷积码都可用这类线性前馈移位寄存器编码器实现。 (0) v (1) v u 图 4.1 速率 R=1/2 的非系统前馈卷积编码器 信息序列 012 u = ( , , ,...) uuu 进入编码器,每次 1 比特,由于编码器是一个线性系统,两 个编码器输出序列 (0) (0) (0) (0) 01 2 v = ( , , ,...) vvv 和 (1) (1) (1) (1) 01 2 v = ( , , ,...) vvv 可通过输入序列 u 和两 个编码器脉冲响应的卷积得到。计算脉冲响应时,可设 u=(1 0 0 … ),然后观测两个输出序 列。对一个具有 m 阶存储器的编码器,脉冲响应能够持续最多 m+1 个时间单元,可写为 (0) (0) (0) (0) (0) 01 2 ( , , ,..., ) m g = ggg g 和 (1) (1) (1) (1) (1) 01 2 ( , , ,..., ) m g = ggg g 。对上图的编码器,有 (0) (1) (1 0 1 1) (1 1 1 1) = = g g (4.1) 脉冲响应 (0) g 和 (1) g 称为编码器的生成器序列。这样,编码方程为: (0) (0) (1) (1) = ⊗ = ⊗ v ug v ug (4.2) 其中⊗ 表示离散卷积,且所有运算都是模 2 加运算,对于所有l ≥ 0,有: ( ) ( ) 0 () () ( ) 0 11 , 0,1 m j j l li i i jj j l l lm m v ug ug u g u g j − = − − = = + ++ = ∑ (4.3) 其中对于所有 l<i, 0 l i u − ,这样对图 4.1 所示的编码器,有: (0) 2 3 (1) 123 ll ll l ll l l vu uu v uu u u − − −− − = ++ =+ + + (4.4)
第四章卷积码的编码 编码后,两个输出序列复用成一个序列,称为码字(codeword),表示为 v=(0,9,0,",,,) (4.5) 例如信息序列u=(10111),则输出序列为: vo,=(10111)⑧(1011)=(10000001) (4.6) v0=(10111)⑧(1111)=(11011101) 复用成一个序列为:v=(11,01,00,01,01,01,00,11) (4.7) 如果将生成器序列g和g写出矩阵形式,为: 「gggg"gg"…gg9 G= g60g”gg…g9g9 gg (4.8) 86g…8,828889g9 其中空白区域为全0,这样编码方程可写为矩阵形式: y=uG (4.9) G称为该编码器的生成矩阵。我们注意到G中的每一行都与前一行相同,只是向右移 位了=2位,它是一个半无限矩阵,对应于信息序列u是一个任意长度的序列。如果u只 有有限长h,则G具有h行、2(m+h)列,v的长度为2(m+h)。例如上例中u=(10111),则 v=uG 「11011111 11011111 =(10111) 11011111 (4.10) 11011111 11011111 =(1101000101010011) 与我们前面的计算一致! =二二===三=三=====三三三 例4.2速率R=23的非系统前馈卷积编码器 v(0 图4.2 Copyright by周武旸
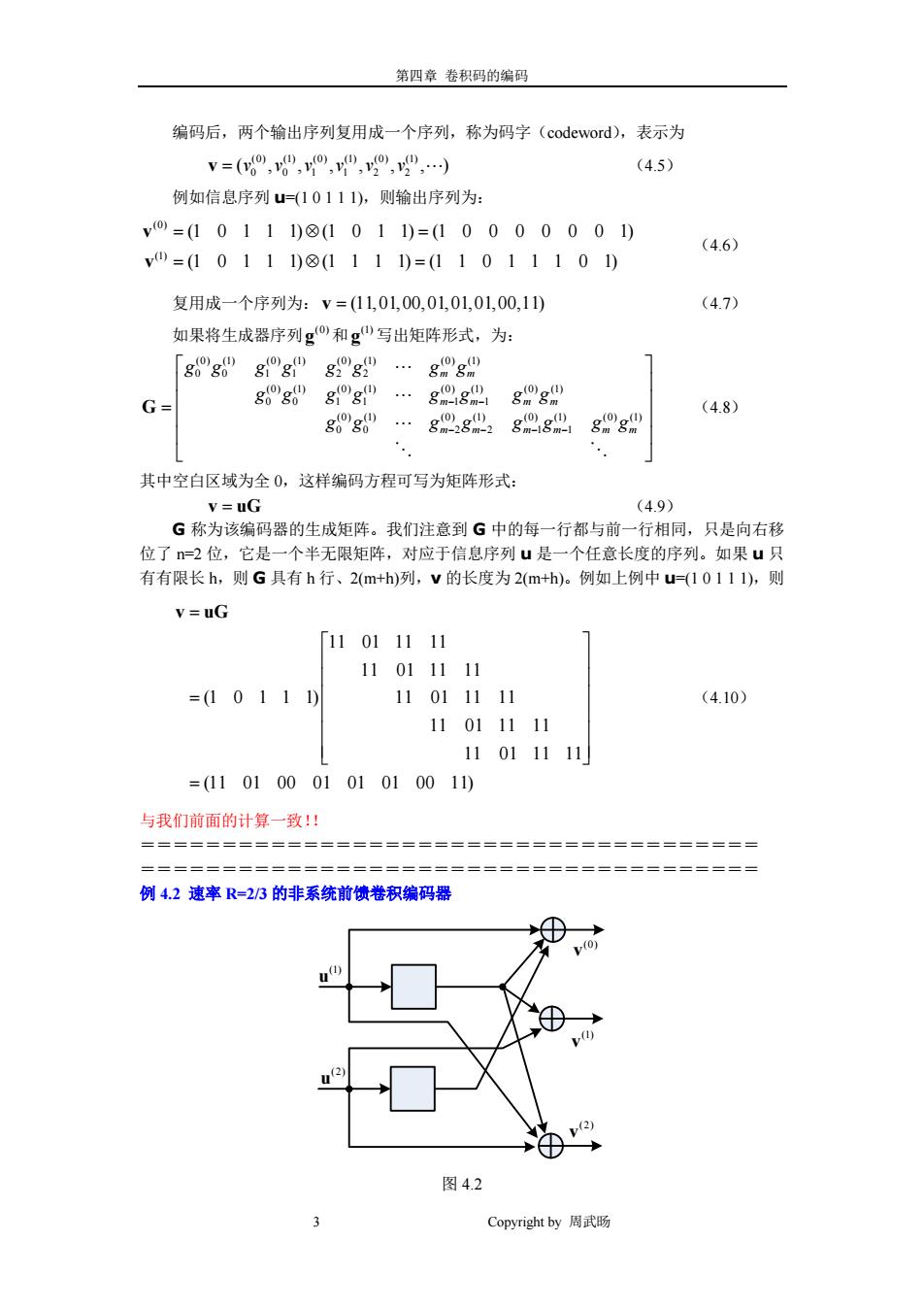
第四章 卷积码的编码 3 Copyright by 周武旸 编码后,两个输出序列复用成一个序列,称为码字(codeword),表示为 (0) (1) (0) (1) (0) (1) 0 01 1 2 2 v = ( , , , , , ,) vvvvvv (4.5) 例如信息序列 u=(1 0 1 1 1),则输出序列为: (0) (1) (1 0 1 1 1) (1 0 1 1) (1 0 0 0 0 0 0 1) (1 0 1 1 1) (1 1 1 1) (1 1 0 1 1 1 0 1) = ⊗= = ⊗= v v (4.6) 复用成一个序列为: v = (11,01,00,01,01,01,00,11) (4.7) 如果将生成器序列 (0) g 和 (1) g 写出矩阵形式,为: (0) (1) (0) (1) (0) (1) (0) (1) 00 11 22 (0) (1) (0) (1) (0) (1) (0) (1) 00 11 1 1 (0) (1) (0) (1) (0) (1) (0) (1) 0 0 2 2 1 1 m m m m mm m m m m mm gg gg gg gg gg gg g g gg gg g g g g gg − − − − −− = G (4.8) 其中空白区域为全 0,这样编码方程可写为矩阵形式: v uG = (4.9) G 称为该编码器的生成矩阵。我们注意到 G 中的每一行都与前一行相同,只是向右移 位了 n=2 位,它是一个半无限矩阵,对应于信息序列 u 是一个任意长度的序列。如果 u 只 有有限长 h,则 G 具有 h 行、2(m+h)列,v 的长度为 2(m+h)。例如上例中 u=(1 0 1 1 1),则 11 01 11 11 11 01 11 11 (1 0 1 1 1) 11 01 11 11 11 01 11 11 11 01 11 11 (11 01 00 01 01 01 00 11) = = = v uG (4.10) 与我们前面的计算一致!! ====================================== ====================================== 例 4.2 速率 R=2/3 的非系统前馈卷积编码器 (0) v (1) v (1) u (2) u (2) v 图 4.2

第四章卷积码的编码 编码速率R=2/3、存储器阶数=1的编码器结构如图4.2所示,该编码器由k=2个移位 寄存器、m=1个时延单元、=3个模2加法器组成。信息序列进入编码器时每次进入k=2 个比特,可写为u=(u,山1,)=(2,42,442,),或作为两个输入序列 u0=(,,”,)和2)=(2,42,2,)。对应于每个输入序列,都有三个生成 器序列。设g=(g,g,,8)表示对应于输入i和输出j的生成器序列,这样我们可 得到图4.2所示编码器的生成器序列为: g0=(11)g"=(0)g2=11) (4.11) g=(01)g=(10)g2=10) 这样我们可写出编码方程如下: vo=u0⑧g0+u②⑧g v=u0⑧g"+u2)图g (4.12) v2=u0⑧g2+u2⑧g2 卷积运算意味着 y0=49+ +唱+2 0= 42+4唱 (4.13) 2=49+42+49 复用后,码字为: V=(2,0"2,"2,) (4.14) 例如:如果u=(101)和u②=(110,则 vo,=(101)⑧(11)+(110)⑧(01)=(1001) v=(101)⑧(01)+(110)⑧(10)=(1001) (4.15) v2)=(101)⑧(11)+(110)⑧(10)=(0011) 所以输出序列为: v=(110,000,001,111) (4.16) 生成矩阵为: g0g1gt g0gHg8…g10mgmg1m 80g8 gYgg…g9gg9 G= sgigt g10-g”g2 (4.17) gE8 g9-80-8gm88 编码方程仍写为v=uG,注意:G中每k=2行都与前2行相同,只是向右移=3位。 如上例中,u0=(101)和u2=(110),则u=(uo,1,u2)=(11,01,10),有: Copyright by周武肠
第四章 卷积码的编码 4 Copyright by 周武旸 编码速率 R=2/3、存储器阶数 m=1 的编码器结构如图 4.2 所示,该编码器由 k=2 个移位 寄存器、m=1 个时延单元、n=3 个模 2 加法器组成。信息序列进入编码器时每次进入 k=2 个比特,可写为 (1) (2) (1) (2) (1) (2) 01 00 11 22 u uu = = (,,)( , , ,) uu uu uu ,或作为两个输入序列 (1) (1) (1) (1) 01 2 u = ( , , ,) uuu 和 (2) (2) (2) (2) 01 2 u = ( , , ,) uuu 。对应于每个输入序列,都有三个生成 器序列。设 () () () () ,0 ,1 , ( , ,, ) j jj j i i i im g = gg g 表示对应于输入 i 和输出 j 的生成器序列,这样我们可 得到图 4.2 所示编码器的生成器序列为: (0) (1) (2) 1 11 (0) (1) (2) 2 22 (1 1) (0 1) (1 1) (0 1) (1 0) (1 0) = = = = = = ggg ggg (4.11) 这样我们可写出编码方程如下: (0) (1) (0) (2) (0) 1 2 (1) (1) (1) (2) (1) 1 2 (2) (1) (2) (2) (2) 1 2 =⊗+⊗ =⊗+ ⊗ =⊗+⊗ vugu g vu gu g vugu g (4.12) 卷积运算意味着 (0) (1) (1) (2) 1 1 (1) (2) (1) 1 (2) (1) (2) (1) 1 l l ll l ll l ll l v u uu v uu v uuu − − − − =+++ = + =++ (4.13) 复用后,码字为: (0) (1) (2) (0) (1) (2) (0) (1) (2) 0 00 1 11 2 22 v = ( , , ,) vvv vvv vvv (4.14) 例如:如果 (1) u = (1 0 1)和 (2) u = (1 1 0) ,则 (0) (1) (2) (101) (11) (110) (01) (1001) (101) (01) (110) (10) (1001) (101) (11) (110) (10) (0011) = ⊗+ ⊗ = = ⊗+ ⊗= = ⊗+ ⊗ = v v v (4.15) 所以输出序列为: v = (110,000,001,111) (4.16) 生成矩阵为: (0) (1) (2) (0) (1) (2) (0) (1) (2) 1,0 1,0 1,0 1,1 1,1 1,1 1, 1, 1, (0) (1) (2) (0) (1) (2) (0) (1) (2) 2,0 2,0 2,0 2,1 2,1 2,1 2, 2, 2, (0) (1) (2) (0) (1) (2) (0) (1) (2) 1,0 1,0 1,0 1, 1 1, 1 1, 1 1, 1, 1, mmm mmm m m m mmm ggg ggg ggg ggg ggg g g g ggg g g g ggg g −−− G = (0) (1) (2) (0) (1) (2) (0) (1) (2) 2,0 2,0 2,0 2, 1 2, 1 2, 1 2, 2, 2, m m m mmm gg g g g g g g −−− (4.17) 编码方程仍写为 v uG = ,注意:G 中每 k=2 行都与前 2 行相同,只是向右移 n=3 位。 如上例中, (1) u = (101) 和 (2) u = (110) ,则 012 u uuu = = ( , , ) (11,01,10) ,有:

第四章卷积码的编码 T101111 011100 101 111 v=uG=(11,01,10) 011100 (4.18) 101111 011100 =(110,000,001,111) 与我们前面的计算一致! ================ 在上两例中,从存储输入序列的k个移位寄存器到个模2加法器的连接,直接对应于 在kn个生成器序列中的非零项,如式(4.1)和(4.11)所示。从上述的例子中可以看出, 当输入序列数k>1时,复杂度明显增加。 下面给出与移位寄存器长度有关的四个定义: 定义4.1:设y,是卷积编码器(有k个输入序列)第i个移位寄存器的长度,i=1,2,k。 例如图4.1中速率R=1/2的编码器,v=3:图4.11中速率R=2/3的编码器,v1=V2=1。 定义4.2:编码器的存储器阶数m定义为: m max vi (4.19) 1≤i≤k 即m是所有k个移位寄存器的最大值。 例如图4.1中速率R=1/2的编码器,m=v1=3:图4.11中速率R=2/3的编码器,m=max(v1,2) =max(1.1=l。 定义4.3:编码器的全局约束长度v定义为: v=∑y (4.20) 即,v是所有k个移位寄存器的总和。 例如图4.1中速率R=1/2的编码器,v=v1=3:图4.11中速率R=2/3的编码器,v=v1+2=2。 定义4.4:全局约束长度为v、编码速率R=kn的卷积编码器常表示为一个(n,k,v)编码器。 例如图4.1中速率R=1/2的编码器是(2,1,3)编码器,图4.11中速率R=2/3的编码器 是(3,2,2)编码器。 因此,对于(n,1,v)编码器,全局约束长度v就等于存储器阶数m。 例4.3:(4,3,3)非系统前馈卷积编码器 (4,3,3)非系统前馈卷积编码器如图4.3所示,寄存器长度v1=0,2=1,=2。存储器 阶数m=2,全局约束长度v=3,生成器序列为: g0=(100)g"=(100)g12=(100)g)=(100) g°=(000)g=(110)g2=(010)g=(100) (4.21) g°=(000)8"=(010)82=(101)g=101) Copyright by周武旸
第四章 卷积码的编码 5 Copyright by 周武旸 101 111 011 100 101 111 (11,01,10) 011 100 101 111 011 100 (110,000,001,111) = = = v uG (4.18) 与我们前面的计算一致!! ===================================== 在上两例中,从存储输入序列的 k 个移位寄存器到 n 个模 2 加法器的连接,直接对应于 在 kn 个生成器序列中的非零项,如式(4.1)和(4.11)所示。从上述的例子中可以看出, 当输入序列数 k>1 时,复杂度明显增加。 下面给出与移位寄存器长度有关的四个定义: 定义 4.1:设 vi是卷积编码器(有 k 个输入序列)第 i 个移位寄存器的长度,i=1, 2,…,k。 例如图 4.1 中速率 R=1/2 的编码器,v=3;图 4.11 中速率 R=2/3 的编码器,v1 = v2 =1。 定义 4.2:编码器的存储器阶数 m 定义为: 1 max i i k m v ≤ ≤ = (4.19) 即 m 是所有 k 个移位寄存器的最大值。 例如图4.1中速率R=1/2的编码器,m=v1=3;图4.11中速率R=2/3的编码器,m=max(v1,v2) =max(1,1)=1。 定义 4.3:编码器的全局约束长度 v 定义为: 1 i i k v v ≤ ≤ = ∑ (4.20) 即,v 是所有 k 个移位寄存器的总和。 例如图 4.1 中速率 R=1/2 的编码器,v=v1=3;图 4.11 中速率 R=2/3 的编码器,v=v1+v2=2。 定义 4.4:全局约束长度为 v、编码速率 R=k/n 的卷积编码器常表示为一个(n,k,v)编码器。 例如图 4.1 中速率 R=1/2 的编码器是(2,1,3)编码器,图 4.11 中速率 R=2/3 的编码器 是(3,2,2)编码器。 因此,对于(n,1,v)编码器,全局约束长度 v 就等于存储器阶数 m。 ======================================= 例 4.3:(4,3,3)非系统前馈卷积编码器 (4,3,3)非系统前馈卷积编码器如图 4.3 所示,寄存器长度 v1=0, v2=1, v3=2。存储器 阶数 m=2,全局约束长度 v=3,生成器序列为: (0) (1) (2) (3) 1 11 1 (0) (1) (2) (3) 2 22 2 (0) (1) (2) (3) 3 33 3 (100) (100) (100) (100) (000) (110) (010) (100) (000) (010) (101) (101) gggg gggg gggg = = = = = = = = = = = = (4.21)

第四章卷积码的编码 u uR) (2 3) 图43(4,3,3)非系统前馈卷积编码器 通常,一个存储器阶数为m的(n,k,v)前馈编码器,其生成矩阵可写为: G。G1G2… G= G。G1…GmGm (4.22) G0… Gm-2 Gm- Gm 其中G,是一个k×n的子矩阵,表示为: gp g 8%-7 G1= g g … 8 (4.23) 89 ε用 … g 仍需要注意的是:生成矩阵G中的k行(一组)都与前k行(一组)相同,只是向右 移n位。对于一个信息序列u=(,u,)=(2.…,4"42…4,),码字 v=uG=(6p"v哈a-,y0y"ym-,…)。 码字v是生成矩阵G的线性组合,因此(n,k,v)是一个线性码。 在线性系统中,时域中的卷积可用更方便的多项式乘法来代替。这样编码方程中每个序 列都可以用一个对应的多项式来代替,例如对一个(2,1,v)编码器,编码方程变为: v(D)=u(D)g(D) (4.24) v(D)=u(D)g(D) 其中 u(D)=4+4D+4D2+… (4.25a) 是信息序列。 6 Copyright by周武旸
第四章 卷积码的编码 6 Copyright by 周武旸 (0) v (1) v (1) u (2) u (2) v (3) u (3) v 图 4.3 (4,3,3)非系统前馈卷积编码器 ======================================= 通常,一个存储器阶数为 m 的(n,k,v)前馈编码器,其生成矩阵可写为: 01 2 01 1 0 21 m m m m mm − − − = GGG G GG G G G G GGG (4.22) 其中Gl 是一个 k×n 的子矩阵,表示为: (0) (1) ( 1) 1, 1, 1, (0) (1) ( 1) 2, 2, 2, (0) (1) ( 1) ,, , n ll l n ll l l n kl kl k l gg g gg g gg g − − − = G (4.23) 仍需要注意的是:生成矩阵 G 中的 k 行(一组)都与前 k 行(一组)相同,只是向右 移 n 位。对于一个信息序列 (1) (2) ( ) (1) (2) ( ) 01 00 0 11 1 (,,)( , ,) k k u uu = = uu u uu u ,码字 (0) (1) ( 1) (0) (1) ( 1) 00 0 11 1 ( , ,) n n vv v vv v − − v uG = = 。 码字 v 是生成矩阵 G 的线性组合,因此(n,k,v)是一个线性码。 在线性系统中,时域中的卷积可用更方便的多项式乘法来代替。这样编码方程中每个序 列都可以用一个对应的多项式来代替,例如对一个(2,1,v)编码器,编码方程变为: (0) (0) (1) (1) () () () () () () D DD D DD = = v ug v ug (4.24) 其中 2 01 2 u( ) D u uD uD =+ + + (4.25a) 是信息序列

第四章卷积码的编码 v0(D)=0+0D+D2+… (4.25b) v(D)=喝+D+0D2+ 是编码后的序列。 g(D)=go)+gD+...+gD" (4.25c) g(D)=g6+g"D+…+g"Dm 是生成多项式。 这样码字可写为: V(D)=[v(D),v"(D)] (4.26a) 或经过复用后,写为: v(D)=v0(D2)+Dv(D2) (4.26b) D可看作为一个时延算子,D的指数表示相对于序列中的初始bit延时了多少时间单元。 例如图4.1所示的(2,1,3)编码器,生成多项式g(D)=1+D2+D3及 g"(D)=1+D+D2+D3,对信息序列u(D)=1+D2+D3+D4,编码方程为: v0(D)=(1+D2+D3+D4)1+D2+D3)=1+D (4.27) v(D)=(1+D2+D3+D4)1+D+D2+D3)=1+D+D3+D4+D+D7 码字可写为: V(D)=[1+D,1+D+D+D+D+D] (4.28a) 或 V(D)=1+D+D3+D'+D+D'+D4+D5 (4.28b) 注意:生成多项式的最低阶项(常数项)对应于移位寄存器连接的最左端,最高阶项对应于 移位寄存器连接的最右端。例如图4.1中,从移位寄存器到输出v0)的连接是g,=(1011), 对应的生成多项式为g(D)=1+D+D。 在(,1,v)编码器中,由于移位寄存器的最右端必须连接到至少一个输出上,因此 至少有一个生成多项式的阶数必然等于移位寄存器的长度m,即 m=max degg((D) (4.29) 05jsn-1 在k>1的(n,k,v)编码器中,对于每个输入(共有k个输入),都有n个生成多项式。 每一组n个生成多项式表示着从移位寄存器到n个输出的连接序列,因此,有 y-max[degg(D)],l≤i≤k (4.30) 其中g”(D)是第个输入到第j个输出的生成多项式。 7 Copyright by周武旸
第四章 卷积码的编码 7 Copyright by 周武旸 (0) (0) (0) (0) 2 01 2 (1) (1) (1) (1) 2 01 2 ( ) ( ) D v vDvD D v vD vD =+ + + =+ + + v v (4.25b) 是编码后的序列。 (0) (0) (0) (0) 0 1 (1) (1) (1) (1) 0 1 ( ) ( ) m m m m D g gD gD D g gD gD = + ++ = + ++ g g (4.25c) 是生成多项式。 这样码字可写为: (0) (1) ( ) ( ), ( ) D DD = V vv (4.26a) 或经过复用后,写为: (0) 2 (1) 2 vv v () ( ) ( ) D DDD = + (4.26b) D 可看作为一个时延算子,D 的指数表示相对于序列中的初始 bit 延时了多少时间单元。 ====================================== 例如图 4.1 所示的( 2 , 1 , 3 )编码器,生成多项式 (0) 2 3 g ()1 D DD =+ + 及 (1) 2 3 g ()1 D DD D =+ + + ,对信息序列 234 u()1 D DDD =+ + + ,编码方程为: (0) 234 23 7 (1) 234 23 3457 ( ) (1 )(1 ) 1 ( ) (1 )(1 ) 1 D DDD DD D D D D D DD D DD D D D = + + + + + =+ = + + + + + + =+ + + + + v v (4.27) 码字可写为: 7 3457 ( ) 1 ,1 D D DD D D D =+ ++ + + + V (4.28a) 或 3 7 9 11 14 15 v()1 D DD D D D D D =+ + + + + + + (4.28b) ====================================== 注意:生成多项式的最低阶项(常数项)对应于移位寄存器连接的最左端,最高阶项对应于 移位寄存器连接的最右端。例如图 4.1 中,从移位寄存器到输出 (0) v 的连接是 (0) g = (1011), 对应的生成多项式为 (0) 2 3 g ()1 D DD =+ + 。 在(n,1,v)编码器中,由于移位寄存器的最右端必须连接到至少一个输出上,因此 至少有一个生成多项式的阶数必然等于移位寄存器的长度 m,即 ( ) 0 1 max deg ( ) j j n m D ≤≤− = g (4.29) 在 k>1 的(n,k,v)编码器中,对于每个输入(共有 k 个输入),都有 n 个生成多项式。 每一组 n 个生成多项式表示着从移位寄存器到 n 个输出的连接序列,因此,有 ( ) 0 1 max deg ( ) , 1 j i i j n v D ik ≤≤− = ≤ ≤ g (4.30) 其中 ( ) ( ) j gi D 是第 i 个输入到第 j 个输出的生成多项式

第四章卷积码的编码 由于编码器是一个线性系统,Ⅱ(D)表示第i个输入序列,v(D)表示第j个输出序 列,生成多项式g(D)可解释为输入i到输出的转移函数。对于有k个输入、n个输出的 线性系统,共有kn个转移函数,可用k×n的生成矩阵表示: g(D)g(D)…ga-(D) … G(D)= g(D)g(D) g-(D) (4.31) g(D)g(D)…g-(D)」 使用生成矩阵,(n,k,v)前馈编码器的编码方程可写为: V(D)-U(D)G(D) (4.32) 其中U(D)u(D),u2(D),…u(D)]是k--tuple 输入序列, V(D)兰[vo(D),v(D),y-(D)]是n--tuple输出序列(码字),复用后,码字可表示 为: v(D)=vo(D")+Dv四(D")+…+D-vm-(D) (4.33) 对于图4.2的(3,2,2)编码器 (0 ⊕D v(D g=(1)g"=(0)g2-11) g=(0)g=10)g2=10) v2) G(D)-D11 1+DD 1+D (4.34) 对于输入序列u(D)=1+D2和u2(D)=1+D,码字为: V(D)=[v(D),v"(D),v2(D)] -+2”1+ (4.35a) =1+D3,1+D3,D2+D] 也可写为: Copyright by周武旸
第四章 卷积码的编码 8 Copyright by 周武旸 由于编码器是一个线性系统, ( ) ( ) i u D 表示第 i 个输入序列, ( ) ( ) j v D 表示第 j 个输出序 列,生成多项式 ( ) ( ) j gi D 可解释为输入 i 到输出 j 的转移函数。对于有 k 个输入、n 个输出的 线性系统,共有 kn 个转移函数,可用 k×n 的生成矩阵表示: (0) (1) ( 1) 11 1 (0) (1) ( 1) 22 2 (0) (1) ( 1) () () () () () () ( ) () () () n n n kk k DD D DD D D DD D − − − = gg g gg g G gg g (4.31) 使用生成矩阵,(n,k,v)前馈编码器的编码方程可写为: V(D)=U(D)G(D) (4.32) 其 中 (1) (2) ( ) ( ) ( ), ( ), ( ) k D DD D U uu u 是 k-tuple 输入序列, (0) (1) ( 1) ( ) ( ), ( ), ( ) n D DD D − V vv v 是 n-tuple 输出序列(码字),复用后,码字可表示 为: (0) (1) 1 ( 1) () ( ) ( ) ( ) n n nn n D DDD D D − − vv v v = + ++ (4.33) ======================================= 对于图 4.2 的(3,2,2)编码器 (0) v (1) v (1) u (2) u (2) v 1 1 ( ) 1 1 DD D D D + + = G (4.34) 对于输入序列 (1) 2 u ()1 D D = + 和 (2) u ()1 D D = + ,码字为: (0) (1) (2) 2 3 3 23 ( ) ( ), ( ), ( ) 1 1 1 ,1 1 1 1 ,1 , D DDD DD D D D D D D DD = + + =+ + =+ + + V vvv (4.35a) 也可写为: (0) (1) (2) 1 11 (0) (1) (2) 2 22 (1 1) (0 1) (1 1) (0 1) (1 0) (1 0) = = = = = = ggg ggg

第四章卷积码的编码 V(D)=1+D+D8+D°+D0+D川 (4.35b) 我们也可以将式(431)、(4.32)、(433)的复用码字v(D)写成: v(D)=(Dg(D) (4.36) 其中 g,(D)=g(D)+Dg"(D)+…+D-g"-(D),1≤i≤k (4.37) 是第i个输入到输出的复合生成多项式。 例如图4.1所示的(2,1,3)编码器,复合生成多项式为: g(D)=g(D2)+Dg(D2) (4.38) =1+D+D3+D4+D3+D+D7 当输入信息多项式u(D)=1+D+D3+D4时,码字为: v(D)=u(D2)g(D) =(1+D+D+D8)1+D+D3+D4+D5+D+D) (4.39) =1+D+D3+D7+D9+D11+D14+D15 卷积编码器的一个重要子类是系统编码器,在一个系统编码器中,前k个输出序列(称 为系统输出序列)正好是k个输入序列的拷贝,即: vi-)=u0,i=1,2,…,k (4.40) 生成器序列满足: gu= (1,if j=i-1 i=1,2,…k (4.41) 0,fj≠i-1 在系统前馈编码器中,生成矩阵可表示为: 「1P。0P0P2…0P G= I。0P…0Pm-10Pnm (4.42) IP。…0Pnm-20Pnm-10Pm 其中I是kXk的单位阵,0是kXk的全0阵,P,是k×(n-k)的矩阵,为: 9 Copyright by周武旸
第四章 卷积码的编码 9 Copyright by 周武旸 8 9 10 11 v()1 D DD D D D =+ + + + + (4.35b) ====================================== 我们也可以将式(4.31)、(4.32)、(4.33)的复用码字 v(D)写成: ( ) 1 () ( )() k i n i i D DD = v ug = ∑ (4.36) 其中 (0) (1) 1 ( 1) () ( ) ( ) ( ), 1 n n nn n ii i D D D D D D ik i − − gg g g = + + + ≤ ≤ (4.37) 是第 i 个输入到输出的复合生成多项式。 ===================================== 例如图 4.1 所示的(2,1,3)编码器,复合生成多项式为: (0) 2 (1) 2 34567 () ( ) ( ) 1 D DDD DD D D D D = + =+ + + + + + gg g (4.38) 当输入信息多项式 234 u()1 D DDD =+ + + 时,码字为: 2 468 34567 3 7 9 11 14 15 ( ) ( )( ) (1 )(1 ) 1 D DD D D D DD D D D D DD D D D D D = =+ + + ++ + + + + =+ + + + + + + v ug (4.39) ====================================== 卷积编码器的一个重要子类是系统编码器,在一个系统编码器中,前 k 个输出序列(称 为系统输出序列)正好是 k 个输入序列的拷贝,即: ( 1) ( ) , 1,2, , i i i k − v u = = (4.40) 生成器序列满足: ( ) 1, 1 1,2, 0, 1 j i if j i i k if j i = − = = ≠ − g (4.41) 在系统前馈编码器中,生成矩阵可表示为: 012 01 1 0 21 m m m m mm − − − = IP 0P 0P 0P IP 0P 0P 0P G IP 0P 0P 0P (4.42) 其中 I 是 k×k 的单位阵,0 是 k×k 的全 0 阵,Pl是k nk × − ( ) 的矩阵,为:

第四章卷积码的编码 g g 8-7 g P= g g5- (4.43) g g ge 类似地,k×n的生成矩阵变为: 0… 0 g(D) g-(D) 01.. 0 … G(D)= g(D) g-(D) (4.44) : 0 0…1 g(D) … g-(D) 由于前k个输出序列是系统的,即为k个输入序列,它们也被称为输出信息序列,后面 的n一k个输出序列被称为输出校验序列。通常,需要kn个生成多项式来定义(n,k,v) 非系统前馈编码器,需要kX(一k)个生成多项式来定义系统前馈编码器。 对于式(4.42)或(4.44)生成矩阵所示的系统前馈编码器,其对应的系统校验矩阵可 直接表示为: P I 0 P I 吲 0 P" 0 P H= (4.45) P0P0P20…P1 P0P0…P0PI P 0…P0P 0P1 其中I是(n-k)×(n-k)的单位阵,0是(n一k)×(n-k)的全零矩阵,类似地,(n 一k)×n的校验矩阵可表示为: g(D) g (D) … g(D) 10. 0 H(D)= g(D)g(D)…g*(D)01 0 (4.46a) g-(D)g-(D)…g-(D)00 1 其中H(D)的后(n一k)列是(n-k)×(n-k)的单位阵,上式也可写为: h(D)h(D)… h-(D)10…0 h(D)h(D)…h-(D)01… H(D)= 0 (4.46b) ho(D)h"(D)…h(D)00 .…1 其中与第(ⅰ一1)个输出信息序列相联系的第(j一k+1)个校验多项式定义为 h(D)=g(D),j=kk+L,,n-l,i=1,2,,k。为了简化表达,可用h(D),i=1, 2,…n-k,j=0,1,…,k-1来表达。 任何一个有效的码字V(或VD)必须满足校验方程: 10 Copyright by周武肠
第四章 卷积码的编码 10 Copyright by 周武旸 ( ) ( 1) ( 1) 1, 1, 1, ( ) ( 1) ( 1) 2, 2, 2, ( ) ( 1) ( 1) ,, , kk n ll l kk n ll l l kk n kl kl k l gg g gg g gg g + − + − + − = P (4.43) 类似地,k×n 的生成矩阵变为: ( ) ( 1) 1 1 ( ) ( 1) 2 2 ( ) ( 1) 1 0 0 () () 01 0 () () ( ) 00 1 () () k n k n k n k k D D D D D D D − − − = g g g g G g g (4.44) 由于前 k 个输出序列是系统的,即为 k 个输入序列,它们也被称为输出信息序列,后面 的 n-k 个输出序列被称为输出校验序列。通常,需要 kn 个生成多项式来定义(n,k,v) 非系统前馈编码器,需要 k×(n-k)个生成多项式来定义系统前馈编码器。 对于式(4.42)或(4.44)生成矩阵所示的系统前馈编码器,其对应的系统校验矩阵可 直接表示为: 0 1 0 21 0 12 0 1 10 21 0 T T T TT T TT T T mm m T T TT m m T TTT m − − − = P I P 0P I P 0P 0P H P 0P 0P 0 P I P 0P 0 P 0P I P 0 P 0P 0P I (4.45) 其中 I 是(n-k)×(n-k)的单位阵,0 是(n-k)×(n-k)的全零矩阵,类似地,(n -k)×n 的校验矩阵可表示为: ( ) ( ) ( ) 1 2 ( 1) ( 1) ( 1) 1 2 ( 1) ( 1) ( 1) 1 2 () () () 1 0 0 () () ()01 0 ( ) () () () 00 1 kk k k kk k k nn n k DD D DD D D DD D ++ + −− − = gg g gg g H gg g (4.46a) 其中 H(D)的后(n-k)列是(n-k)×(n-k)的单位阵,上式也可写为: (0) (1) ( 1) 11 1 (0) (1) ( 1) 22 2 (0) (1) ( 1) () () ()1 0 0 () () () 01 0 ( ) () () () 00 1 k k k nk nk n k DD D DD D D DD D − − − −− − = hh h hh h H hh h (4.46b) 其中与第(i-1)个输出信息序列相联系的第(j-k+1)个校验多项式定义为 ( 1) ( ) 1() () i j j k D D i − h g − + = ,j=k, k+1, …, n-1,i=1, 2, …, k。为了简化表达,可用 ( ) ( ) j hi D ,i=1, 2,…,n-k,j=0,1,…,k-1 来表达。 任何一个有效的码字 v(或 V(D))必须满足校验方程: