
第7章信道编码 1
第7章 信道编码 1

本章内容 ”绪论 冬线性分组码 冬循环码 卷积码 &Turbo码
本章内容 绪论 线性分组码 循环码 卷积码 Turbo码 2

7.1引言 。在设计数字通信系统时,首先应从合理地选择调制解调方法、合适的发 射功率等方面考虑,若仍不能满足系统误码率要求,则要考虑采用本章 所讲的差错控制编码措施。 纠错码,是当消息经过有噪信道传输或要恢复存储的数据时用来纠错的 。用来传输消息的物理介质叫做信道(如电话线、卫星连接、用于移动 通信的无线信道等)。因为纠错码试图克服信道中噪声造成的损害,因 此其编码过程又称为信道编码,它是提高数字信号传输可靠性的有效方 法之一。 信道 信源 调制器 编码器 信道 噪声 信道 信宿 解调器 译码器 差错控制编码: 编码调制
3 7.1 引 言 在设计数字通信系统时,首先应从合理地选择调制解调方法、合适的发 射功率等方面考虑,若仍不能满足系统误码率要求,则要考虑采用本章 所讲的差错控制编码措施。 纠错码,是当消息经过有噪信道传输或要恢复存储的数据时用来纠错的 。用来传输消息的物理介质叫做信道(如电话线、卫星连接、用于移动 通信的无线信道等)。因为纠错码试图克服信道中噪声造成的损害,因 此其编码过程又称为信道编码,它是提高数字信号传输可靠性的有效方 法之一。 信源 信宿 信道 编码器 信道 译码器 调制器 解调器 信道 噪声 差错控制编码 编码调制

信道编码可分为两个研究领域:波形编码(信号设计)和结构化序列(结 构冗余)。波形编码是将波形转变为“更好的波形”以减少错误判决;结 构化序列是将数据序列转变为“更好的序列”,通过冗余比特来检测和纠 正传输中的错误。 波形编码:最常见的是正交编码和双正交编码,通过编码使编码集合中信 号间的相关度最小(即信号间的距离最大)。如对极信号、正交信号。正 交编码常使用Hadamard矩阵,即1bit数据集可用两个数字的正交码字进 行变换,2bit数据集可使用4个数字的正交码字进行变换,依此类推。 数据集 正交码字集 数据集 正交码字集 10 H=〔8) 00 01 f88 10 H2 0 11 Hk= HK-1 HK-i Hk-i
信道编码可分为两个研究领域:波形编码(信号设计)和结构化序列(结 构冗余)。波形编码是将波形转变为“更好的波形”以减少错误判决;结 构化序列是将数据序列转变为“更好的序列” ,通过冗余比特来检测和纠 正传输中的错误。 波形编码:最常见的是正交编码和双正交编码,通过编码使编码集合中信 号间的相关度最小(即信号间的距离最大)。如对极信号、正交信号。正 交编码常使用Hadamard矩阵,即1bit数据集可用两个数字的正交码字进 行变换,2bit数据集可使用4个数字的正交码字进行变换,依此类推。 数据集 1 0 正交码字集 H1= 0 0 0 1 数据集 正交码字集 0 0 0 1 1 0 1 1 H2= 0 0 0 0 0 1 0 1 0 0 1 1 0 1 1 0 = H1 H1 H1 H1 Hk= Hk-1 Hk-1 Hk-1 Hk-1 4

双正交码:具有M个信号的双正交信号集可由M/2个信号的正交信 号集获取。 BM= Hm-i HM-1 %例如,一个3bt数据集可以转变为如下的双正交码字集 数据集 正交码字集 000 0000 011 0101 010 0011 011 0110 B3= 100 1111 10 1 1010 110 1100 111 1001 5
双正交码:具有M个信号的双正交信号集可由M/2个信号的正交信 号集获取。 例如,一个3bit数据集可以转变为如下的双正交码字集 BM= HM-1 HM-1 数据集 正交码字集 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 B3= 0 0 0 0 0 1 0 1 0 0 1 1 0 1 1 0 1 1 1 1 1 0 1 0 1 1 0 0 1 0 0 1 5

常用的差错控制方式有三种: 检错重发方式,又称为自动重发请求(ARQ),发送端发送能够 发现错误的码,由接收端判断接收中有无错误发生。如果发现错 误,则通过反向信道把这一判决结果反馈给发送端,然后发送端 再把错误的信息重发一次。 能够发现错误的码 发送端 接收端 应答信号 前向纠错方式(FEC):发送端发送能够纠正错误的码,接收 端收到后自动纠正传输中的错误,特点是单向传输。 可以纠正错误的码 发送端 接收端 6
6 常用的差错控制方式有三种: 检错重发方式,又称为自动重发请求(ARQ),发送端发送能够 发现错误的码,由接收端判断接收中有无错误发生。如果发现错 误,则通过反向信道把这一判决结果反馈给发送端,然后发送端 再把错误的信息重发一次。 发送端 接收端 能够发现错误的码 应答信号 前向纠错方式(FEC):发送端发送能够纠正错误的码,接收 端收到后自动纠正传输中的错误,特点是单向传输。 发送端 接收端 可以纠正错误的码
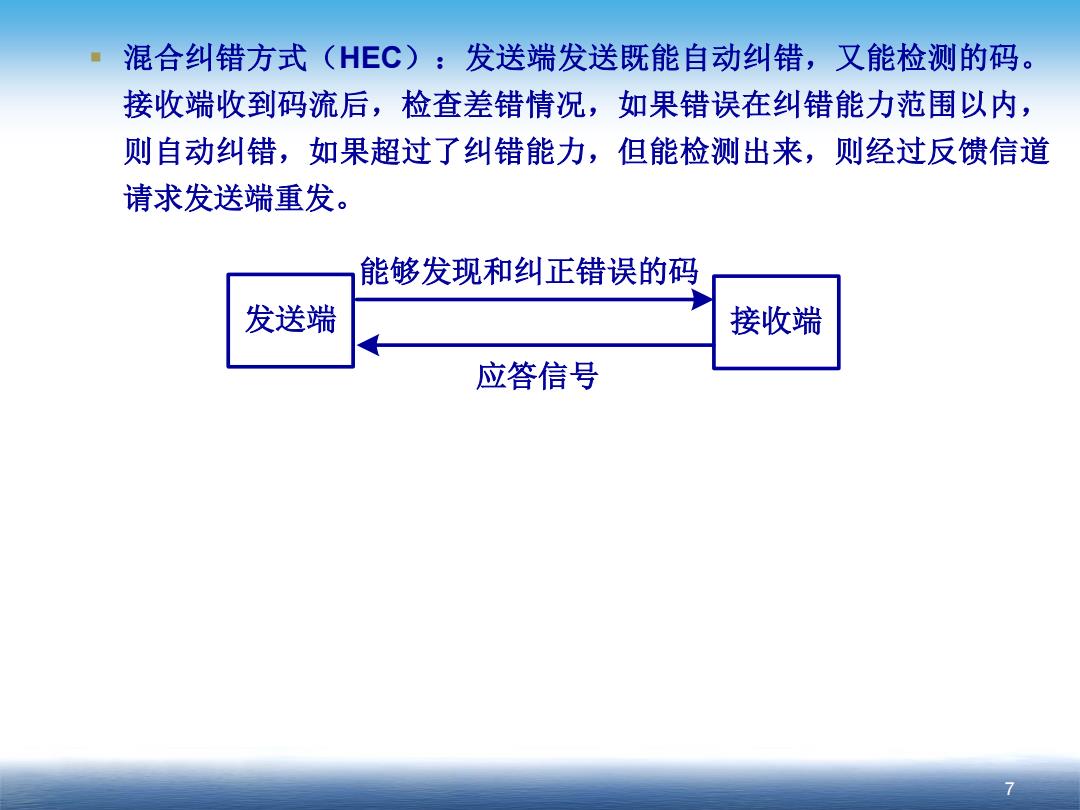
·混合纠错方式(HEC):发送端发送既能自动纠错,又能检测的码。 接收端收到码流后,检查差错情况,如果错误在纠错能力范围以内, 则自动纠错,如果超过了纠错能力,但能检测出来,则经过反馈信道 请求发送端重发。 能够发现和纠正错误的码 发送端 接收端 应答信号
7 混合纠错方式(HEC):发送端发送既能自动纠错,又能检测的码。 接收端收到码流后,检查差错情况,如果错误在纠错能力范围以内, 则自动纠错,如果超过了纠错能力,但能检测出来,则经过反馈信道 请求发送端重发。 发送端 接收端 能够发现和纠正错误的码 应答信号

7.1.1差错控制编码理论的起源和发展 1948年,Bell实验室的C.E.Shannon发表的《通信的数学理论》,是关于 现代信息理论的奠基性论文,它的发表标志着信息与编码理论这一学科 的创立。Shannon在该文中指出,任何一个通信信道都有确定的信道容量 C,如果通信系统所要求的传输速率R小于C,则存在一种编码方法,当 码长n充分大并应用最大似然译码(MLD,Maximum Likelihood Decoding)时,信息的错误概率可以达到任意小。从Shannon信道编码定 理可知,随着分组码的码长或卷积码的约束长度N的增加,系统可以取 得更好的性能(即更大的保护能力或编码增益),而译码的最优算法是 MLD,MLD算法的复杂性随n或N的增加呈指数增加,因此当n或N较大 时,MLD在物理上是不可实现的。因此,构造物理可实现编码方案及寻 找有效译码算法一直是信道编码理论与技术研究的中心任务。 Shannon?指出了可以通过差错控制码在信息传输速率不大于信道容量的前 提下实现可靠通信,但却没有给出具体实现差错控制编码的方法。 8
8 7.1.1 差错控制编码理论的起源和发展 1948年,Bell实验室的C.E.Shannon发表的《通信的数学理论》,是关于 现代信息理论的奠基性论文,它的发表标志着信息与编码理论这一学科 的创立。Shannon在该文中指出,任何一个通信信道都有确定的信道容量 C,如果通信系统所要求的传输速率R小于C,则存在一种编码方法,当 码 长 n 充分大并应用最大似然译码 ( MLD , Maximum Likelihood Decoding)时,信息的错误概率可以达到任意小。从Shannon信道编码定 理可知,随着分组码的码长n或卷积码的约束长度N的增加,系统可以取 得更好的性能(即更大的保护能力或编码增益),而译码的最优算法是 MLD,MLD算法的复杂性随n或N的增加呈指数增加,因此当n或N较大 时,MLD在物理上是不可实现的。因此,构造物理可实现编码方案及寻 找有效译码算法一直是信道编码理论与技术研究的中心任务。 Shannon指出了可以通过差错控制码在信息传输速率不大于信道容量的前 提下实现可靠通信,但却没有给出具体实现差错控制编码的方法

20世纪40年代,R.Hamming和M.Golay提出了第一个实用的差错控制 编码方案,使编码理论这个应用数学分支的发展得到了极大的推动。 通常认为是R.Hamming提出了第一个差错控制码。当时他作为一个数 学家受雇于贝尔实验室,主要从事弹性理论的研究。他发现计算机经 常在计算过程中出现错误,而一旦有错误发生,程序就会停止运行。 这个问题促使他编制了使计算机具有检测错误能力的程序,通过对输 入数据编码,使计算机能够纠正这些错误并继续运行。Hamming所采 用的方法就是将输入数据每4个比特分为一组,然后通过计算这些信息 比特的线性组合来得到3个校验比特,然后将得到的7个比特送入计算 机。计算机按照一定的原则读取这些码字,通过采用一定的算法,不 仅能够检测到是否有错误发生,同时还可以找到发生单个比特错误的 比特的位置,该码可以纠正7个比特中所发生的单个比特错误。这个编 码方法就是分组码的基本思想,Hamming提出的编码方案后来被命名 为汉明码。 9
9 20世纪40年代,R.Hamming和M.Golay提出了第一个实用的差错控制 编码方案,使编码理论这个应用数学分支的发展得到了极大的推动。 通常认为是R.Hamming提出了第一个差错控制码。当时他作为一个数 学家受雇于贝尔实验室,主要从事弹性理论的研究。他发现计算机经 常在计算过程中出现错误,而一旦有错误发生,程序就会停止运行。 这个问题促使他编制了使计算机具有检测错误能力的程序,通过对输 入数据编码,使计算机能够纠正这些错误并继续运行。Hamming所采 用的方法就是将输入数据每4个比特分为一组,然后通过计算这些信息 比特的线性组合来得到3个校验比特,然后将得到的7个比特送入计算 机。计算机按照一定的原则读取这些码字,通过采用一定的算法,不 仅能够检测到是否有错误发生,同时还可以找到发生单个比特错误的 比特的位置,该码可以纠正7个比特中所发生的单个比特错误。这个编 码方法就是分组码的基本思想,Hamming提出的编码方案后来被命名 为汉明码

虽然汉明码的思想是比较先进的,但是它也存在许多难以接受的缺点。 首先,汉明码的编码效率比较低,它每4个比特编码就需要3个比特的冗 余校验比特。另外,在一个码组中只能纠正单个的比特错误。M.Goay 研究了汉明码的这些缺点,并提出了两个以他自己的名字命名的高性能 码字:一个是二元Golayi码,在这个码字中Golay将信息比特每12个分为 一组,编码生成11个冗余校验比特。相应的译码算法可以纠正3个错误 。另外一个是三元Goay码,它的操作对象是三元而非二元数字。三元 Golay码将每6个三元符号分为一组,编码生成5个冗余校验三元符号。 这样由11个三元符号组成的三元Golay码码字可以纠正2个错误。 10
10 虽然汉明码的思想是比较先进的,但是它也存在许多难以接受的缺点。 首先,汉明码的编码效率比较低,它每4个比特编码就需要3个比特的冗 余校验比特。另外,在一个码组中只能纠正单个的比特错误。M.Golay 研究了汉明码的这些缺点,并提出了两个以他自己的名字命名的高性能 码字:一个是二元Golay码,在这个码字中Golay将信息比特每12个分为 一组,编码生成11个冗余校验比特。相应的译码算法可以纠正3个错误 。另外一个是三元Golay码,它的操作对象是三元而非二元数字。三元 Golay码将每6个三元符号分为一组,编码生成5个冗余校验三元符号。 这样由11个三元符号组成的三元Golay码码字可以纠正2个错误