
第6章同步技术
第6章 同步技术

本章内容 冬概述 。载波同步 载波同步系统的性能 冬位同步(码元同步) 冬位同步系统的性能 。群同步(帧同步)
本章内容 概述 载波同步 载波同步系统的性能 位同步(码元同步) 位同步系统的性能 群同步(帧同步)
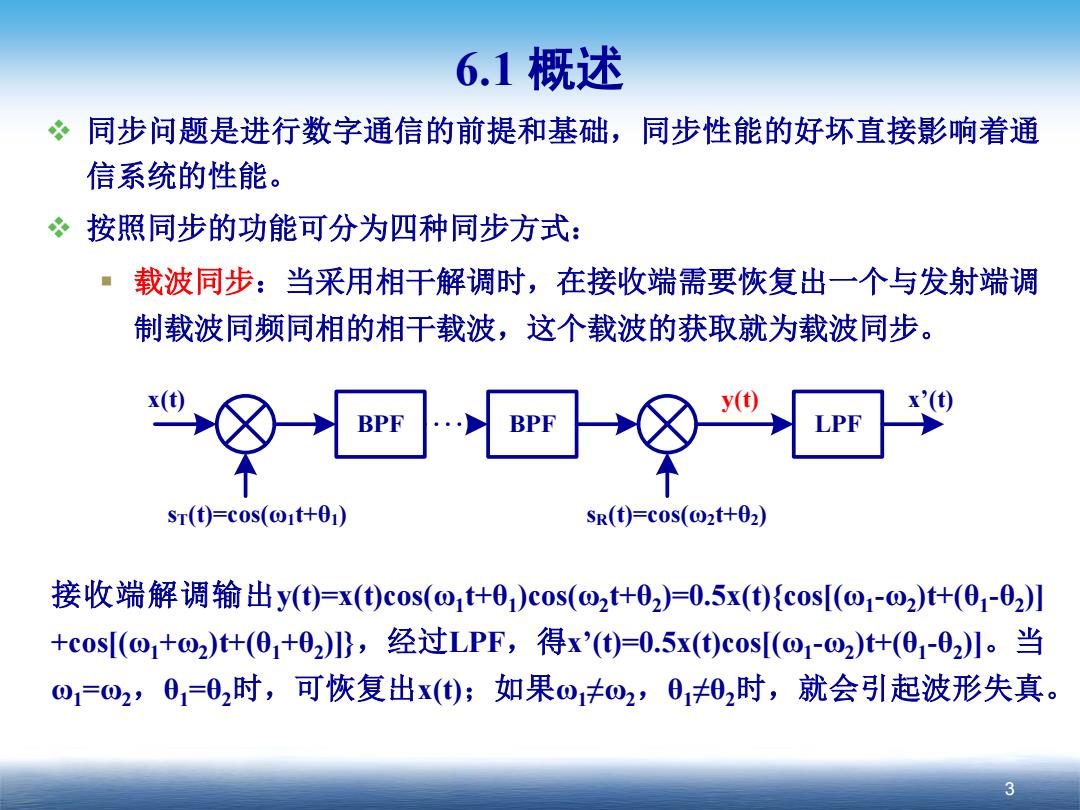
6.1概述 ·同步问题是进行数字通信的前提和基础,同步性能的好坏直接影响着通 信系统的性能。 按照同步的功能可分为四种同步方式: 载波同步:当采用相干解调时,在接收端需要恢复出一个与发射端调 制载波同频同相的相干载波,这个载波的获取就为载波同步。 BPF BPF LPF ST(t)=cos(@1t+01) SR(t)=cos(@2t+02) 接收端解调输出y()=x()cos(o1t+01)cos(o2t+02)=0.5x()Kc0s[(o1-Q2)t+(01-02)川 +c0s(o1+o2)+(01+02),经过LPF,得x')=0.5x()cos[(o1o2)t+(01-02)】。当 01=02,0=02时,可恢复出x();如果o1≠o2,0102时,就会引起波形失真
3 6.1 概述 同步问题是进行数字通信的前提和基础,同步性能的好坏直接影响着通 信系统的性能。 按照同步的功能可分为四种同步方式: 载波同步:当采用相干解调时,在接收端需要恢复出一个与发射端调 制载波同频同相的相干载波,这个载波的获取就为载波同步。 x(t) sT(t)=cos(ω1t+θ1) sR(t)=cos(ω2t+θ2) BPF BPF LPF y(t) x’(t) 接收端解调输出y(t)=x(t)cos(ω1t+θ1)cos(ω2t+θ2)=0.5x(t){cos[(ω1-ω2)t+(θ1-θ2)] +cos[(ω1+ω2)t+(θ1+θ2)]},经过LPF,得x’(t)=0.5x(t)cos[(ω1-ω2)t+(θ1-θ2)]。当 ω1=ω2,θ1=θ2时,可恢复出x(t);如果ω1≠ω2,θ1≠θ2时,就会引起波形失真

位同步:消息由一系列码元组成,这些码元具有相同的持续时间 (T、),接收端接收该码元序列时,需知道每个码元的起止时刻,以 便判别。即对信号进行抽样判决时,码元定时脉冲序列的重复频率应 与发送端的码元速率相同,抽样判决时刻对准每个码元最大值的位置 (最佳抽样判决位置),这个过程就是位同步或码元同步。 群同步(帧同步):数字信息在传输前,总是由若干码元组成一个帧 进行发送,接收时,必须知道这些帧的起止时刻。在接收端产生与帧 起止时刻相一致的定时脉冲序列,称为帧同步。 网同步:让整个数字通信网有一个统一的时间节拍标准,保证通信网 中各用户之间可靠地进行数据交换。 按不同的传输方式,分: ·外同步法:发送端发送特定的同步信息以便接收端进行检测、同 步的方法称为外同步法。 自同步法:发送端不发送特定的同步信息,而是从接收信号中提 取同步信息
位同步:消息由一系列码元组成,这些码元具有相同的持续时间 (Ts),接收端接收该码元序列时,需知道每个码元的起止时刻,以 便判别。即对信号进行抽样判决时,码元定时脉冲序列的重复频率应 与发送端的码元速率相同,抽样判决时刻对准每个码元最大值的位置 (最佳抽样判决位置),这个过程就是位同步或码元同步。 群同步(帧同步):数字信息在传输前,总是由若干码元组成一个帧 进行发送,接收时,必须知道这些帧的起止时刻。在接收端产生与帧 起止时刻相一致的定时脉冲序列,称为帧同步。 网同步:让整个数字通信网有一个统一的时间节拍标准,保证通信网 中各用户之间可靠地进行数据交换。 按不同的传输方式,分: 外同步法:发送端发送特定的同步信息以便接收端进行检测、同 步的方法称为外同步法。 自同步法:发送端不发送特定的同步信息,而是从接收信号中提 取同步信息

6.2载波同步 若已调信号本身含有足够的载频分量,就可直接用窄带ltr滤出,如无法 从已调信号中直接分离出载波信息,就用外同步方法来实现。因此载波同 步的方法通常有直接法(自同步法)和插入导频法(外同步法)两种。 。直接法又可分为非线性变换一滤波法和特殊锁相环法。 插入导频法也可分为两种:频域插入,即在发送信息的频谱中或频带外插 入相关的导频;时域插入,即在一定的时段上传送载波信息
5 6.2 载波同步 若已调信号本身含有足够的载频分量,就可直接用窄带filter滤出,如无法 从已调信号中直接分离出载波信息,就用外同步方法来实现。因此载波同 步的方法通常有直接法(自同步法)和插入导频法(外同步法)两种。 直接法又可分为非线性变换-滤波法和特殊锁相环法。 插入导频法也可分为两种:频域插入,即在发送信息的频谱中或频带外插 入相关的导频;时域插入,即在一定的时段上传送载波信息
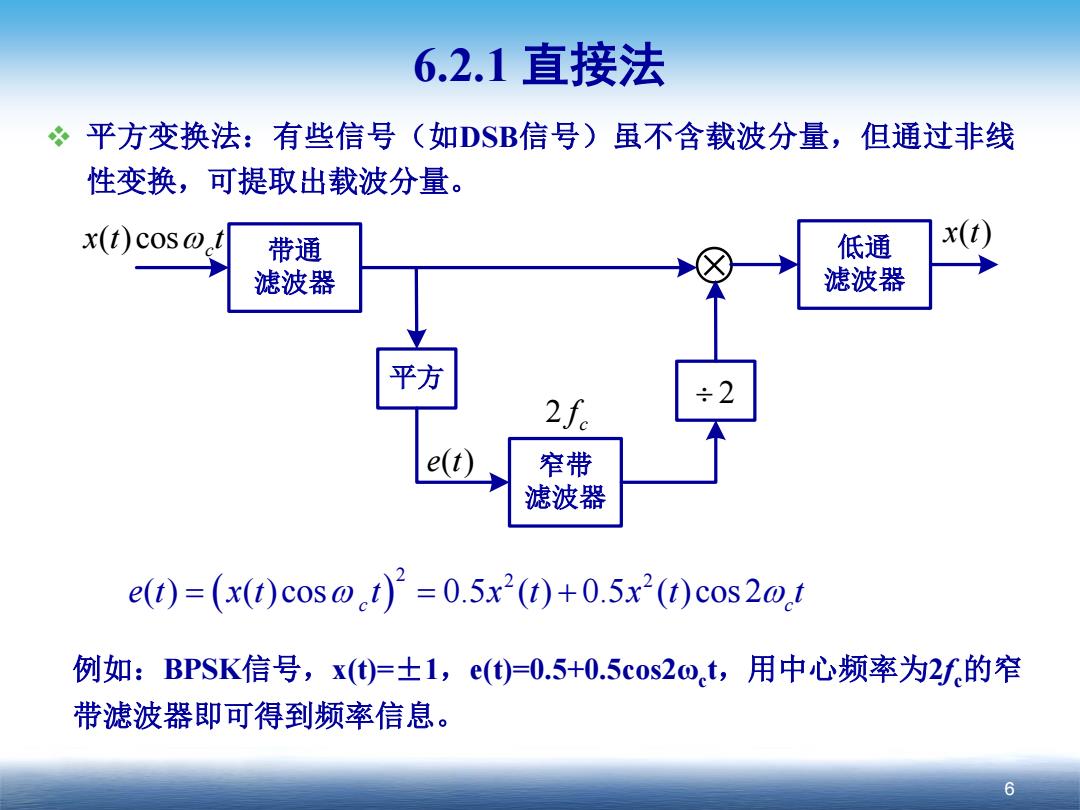
6.2.1直接法 平方变换法:有些信号(如DSB信号)虽不含载波分量,但通过非线 性变换,可提取出载波分量。 x(t)cos@ 带通 低通 滤波器 滤波器 平方 2f. e(t 窄带 滤波器 e(t)=(x(t)cos0.t)=0.5x2()+0.5x2(t)cos2o,t 例如:BPSK信号,x(①)=士1,e()=0.5+0.5cos2ot,用中心频率为2f的窄 带滤波器即可得到频率信息。 6
6 6.2.1 直接法 平方变换法:有些信号(如DSB信号)虽不含载波分量,但通过非线 性变换,可提取出载波分量。 带通 滤波器 ⊗ 低通 滤波器 窄带 滤波器 平方 ÷ 2 x t t ωc ( ) cos c 2 f x(t) e(t) ( ) 2 2 2 ( ) ( )cos 0.5 ( ) 0.5 ( )cos 2 c c et xt t x t x t t = ω ω = + 例如:BPSK信号,x(t)=±1,e(t)=0.5+0.5cos2ωct,用中心频率为2fc的窄 带滤波器即可得到频率信息
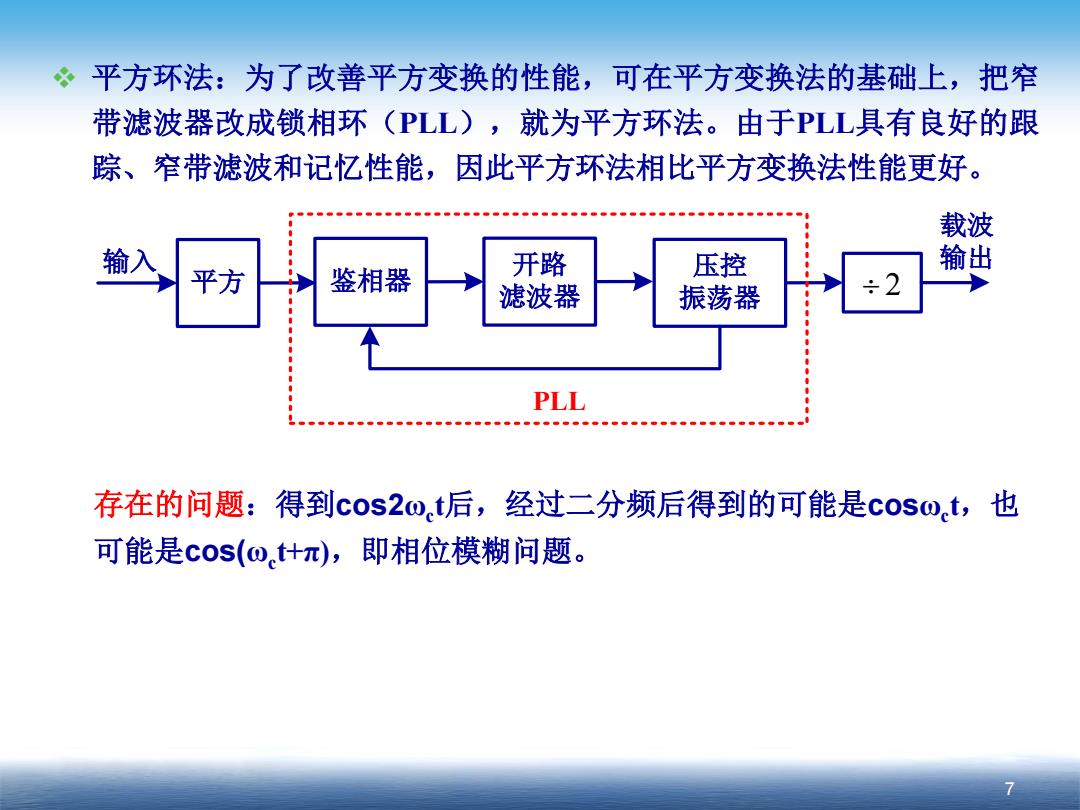
8 平方环法:为了改善平方变换的性能,可在平方变换法的基础上,把窄 带滤波器改成锁相环(PLL),就为平方环法。由于PLL具有良好的跟 踪、窄带滤波和记忆性能,因此平方环法相比平方变换法性能更好。 载波 输 开路 压控 输出 平方 鉴相器 滤波器 振荡器 ÷2 PLL 存在的问题:得到cos20.t后,经过二分频后得到的可能是cos0t,也 可能是cos(o+π),即相位模糊问题
7 平方环法:为了改善平方变换的性能,可在平方变换法的基础上,把窄 带滤波器改成锁相环(PLL),就为平方环法。由于PLL具有良好的跟 踪、窄带滤波和记忆性能,因此平方环法相比平方变换法性能更好。 平方 压控 振荡器 ÷ 2 输入 鉴相器 PLL 载波 开路 输出 滤波器 存在的问题:得到cos2ωct后,经过二分频后得到的可能是cosωct,也 可能是cos(ωct+π),即相位模糊问题
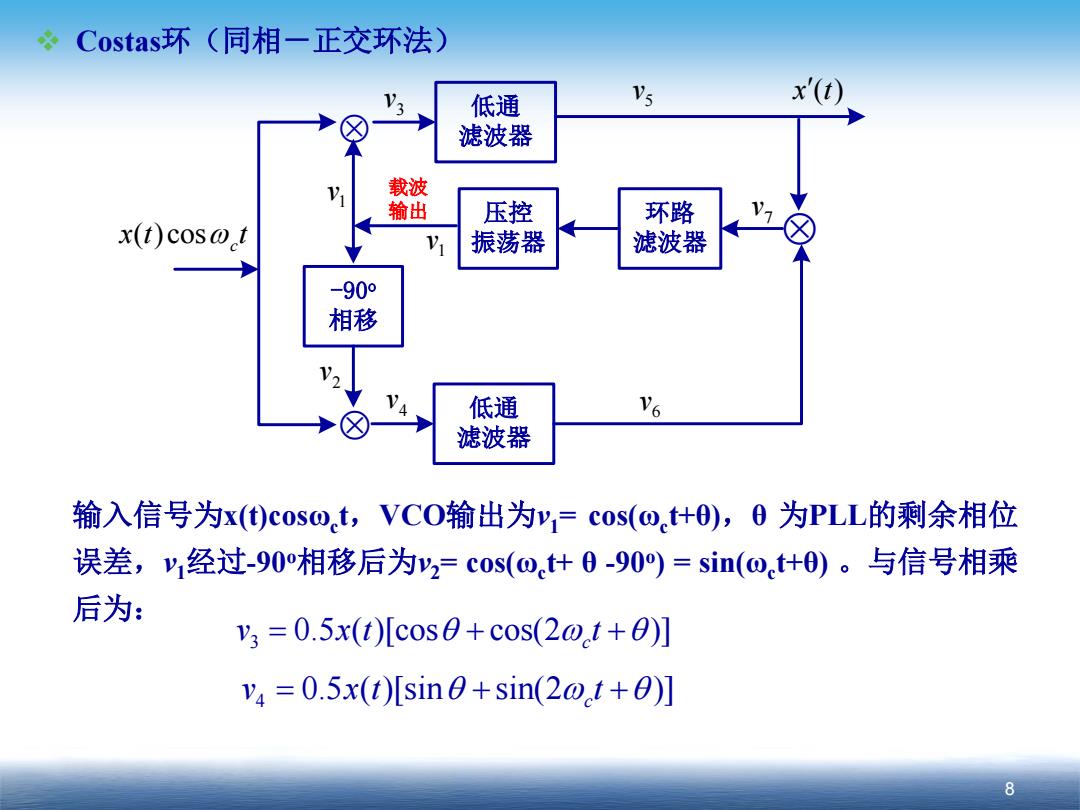
Costas环(同相一正交环法) 低通 V5 x'(t) 滤波器 载波 输出 压控 环路 x(t)cos@t y 振荡器 滤波器 -90° 相移 低通 V6 滤波器 输入信号为x()cos@.t,VCO输出为y,=cos(o.t什0),0为PLL的剩余相位 误差,y1经过-90相移后为y2=c0s(o什0-90)=sin(o+0)。与信号相乘 后为: y3=0.5x(t)[cos0+c0s(20t+0)] v4=0.5x(t)[sin0+sin(2o.t+0)] 8
8 Costas环(同相-正交环法) ⊗ x t t ωc ( ) cos x ′(t) ⊗ 低通 滤波器 压控 振荡器 环路 滤波器 ⊗ -90o 相移 低通 滤波器 载波 输出 1 v 2 v 3 v 4 v 5 v 6 v 7 v 1 v 输入信号为x(t)cosωct,VCO输出为v1= cos(ωct+θ),θ 为PLL的剩余相位 误差,v1经过-90o相移后为v2= cos(ωct+ θ -90o) = sin(ωct+θ) 。与信号相乘 后为: 3 0.5 ( )[cos cos(2 )] c v xt = ++ θ ωθ t 4 0.5 ( )[sin sin(2 )] c v xt = ++ θ ωθ t

经过低通滤波器后,得: y=2x()c0s8 =0sn0 经过乘法器后, ,-8r0sm20*8r0-20=子x0-0 这个电压经过环路滤波器后控制VCO使它与O,同频,相位只差一个很 小的0。此时,y=cos(o+0)就是需要提取的同步载波,而 s=0.5x()c0s0≈0.5x()就是解调器的输出。 注意:当y=cos(o+0+180)时,经计算会得到相同的的y,值,因此y1 的相位也是不确定的。 9
9 经过低通滤波器后,得: 经过乘法器后, 这个电压经过环路滤波器后控制VCO使它与ωc同频,相位只差一个很 小的θ 。此时, v1= cos(ωct+θ)就是需要提取的同步载波,而 v5= 0.5x(t)cosθ ≈ 0.5x(t) 就是解调器的输出。 注意:当v1= cos(ωct+θ+180o)时,经计算会得到相同的的v7值,因此v1 的相位也是不确定的。 5 1 ( )cos 2 v xt = θ 6 1 ( )sin 2 v xt = θ 2 22 7 1 11 ( )sin 2 ( ) 2 ( ) 8 84 v xt xt xt = ≈ ⋅= ⋅ θ θθ
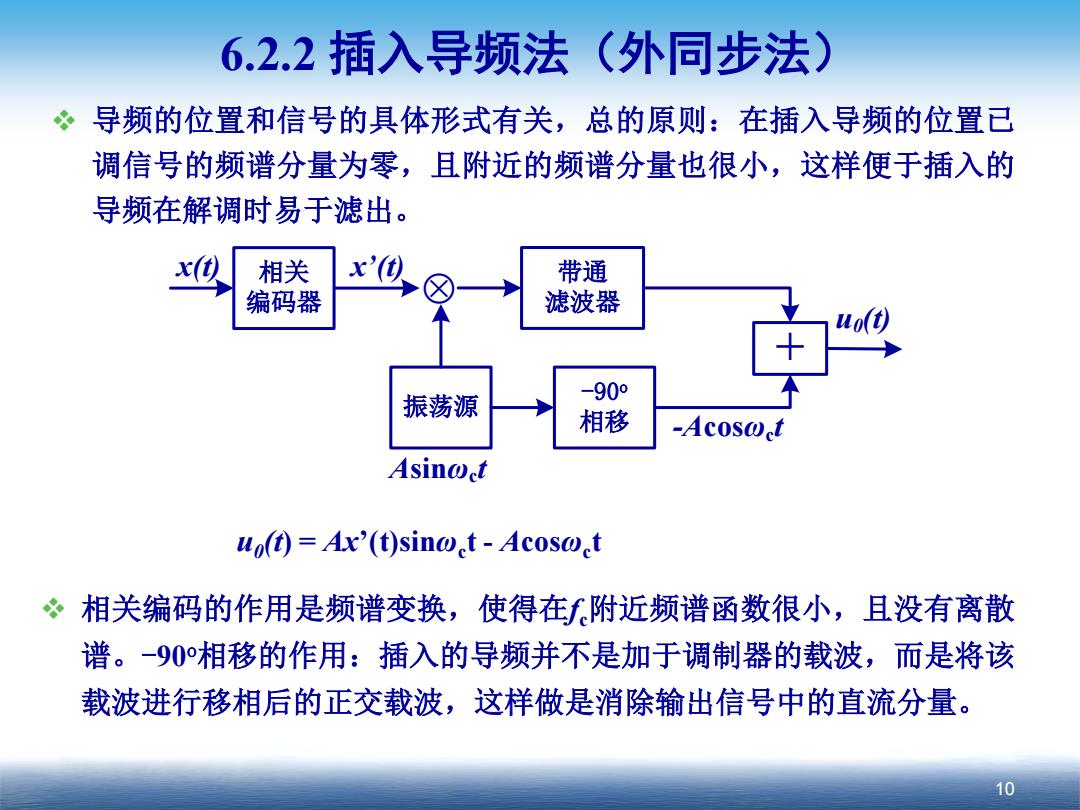
6.2.2插入导频法(外同步法) 导频的位置和信号的具体形式有关,总的原则:在插入导频的位置已 调信号的频谱分量为零,且附近的频谱分量也很小,这样便于插入的 导频在解调时易于滤出。 相关 x( 带通 编码器 滤波器 振荡源 -90° 相移 -Acoso.t Asin@ct up(t)=Ax'(t)sino.t-Acosoct 。相关编码的作用是频谱变换,使得在f附近频谱函数很小,且没有离散 谱。-90°相移的作用:插入的导频并不是加于调制器的载波,而是将该 载波进行移相后的正交载波,这样做是消除输出信号中的直流分量。 10
10 6.2.2 插入导频法(外同步法) 导频的位置和信号的具体形式有关,总的原则:在插入导频的位置已 调信号的频谱分量为零,且附近的频谱分量也很小,这样便于插入的 导频在解调时易于滤出。 ⊗ 带通 滤波器 振荡源 -90o 相移 + 相关 编码器 Asinωct -Acosωct x(t) u0(t) x’(t) 相关编码的作用是频谱变换,使得在fc附近频谱函数很小,且没有离散 谱。-90o相移的作用:插入的导频并不是加于调制器的载波,而是将该 载波进行移相后的正交载波,这样做是消除输出信号中的直流分量。 u0(t) = Ax’(t)sinωct - Acosωct